开放科学（资源服务）标志码（OSID）：

0 概述

卷积神经网络良好的学习能力使得深度学习、人工智能得到快速发展^[1]，人脸识别、目标跟踪等技术的应用变得越来越广泛，如手机人脸解锁、无人驾驶汽车等。在无人驾驶领域，图像质量与乘客安全密切相关，在雾天情况下，空气中存在大量悬浮颗粒物，它们对光线产生散射，使物体反射的光线衰减^[2]，同时，这种反射光与观察者接收的光线发生混合，造成观察者获取到的图像对比度、清晰度等特征发生改变，细节信息大量丢失^[3]，这对人类的视觉感知以及许多依赖计算机视觉的智能系统而言都是一个巨大挑战。

近年来，随着图像去雾相关研究的不断发展，出现了很多优秀的去雾算法，其中，应用较广泛的是直方图均衡化去雾算法、暗通道先验去雾（DCP）算法^[4]、基于神经网络的去雾算法等，这些算法可以分成基于手工先验、基于学习先验两大类。

基于手工先验的方法需要人手工制作图像先验，具有代表性的算法是暗通道先验算法，该算法基于大气散射物理学模型，通过使用图像像素点先验来估计透射率，其复杂度较低，然而，当场景对象与大气光值相似时，该算法去雾效果不佳。此外，ZHU等^[5]提出一种结构简单但性能强大的颜色衰减先验算法，该算法为估计有雾图像的场景深度建立了一种线性模型。BERMAN^[6]提出一种非局部先验来重建原始的无雾图像，该算法假设无雾图像的颜色由数百种不同的颜色近似并在RGB空间中形成紧密集群。尽管上述方法取得了一定的成功，但是基于手工先验的方法并不能很好地处理所有情况，且去雾处理后的图片存在颜色失真的问题。

基于学习先验的方法使用卷积神经网络或生成对抗网络（Generative Adversarial Network，GAN）^[7]模型，通过大量的训练数据训练模型使其拥有去雾的能力。CAI^[8]提出一种基于卷积神经网络的端到端去雾模型DehazeNet，该模型以有雾图像作为输入，输出其介质透射图，并通过大气散射模型重建无雾图像。与之类似，ZHANG^[9-10]也采用深度卷积神经网络来估计透射图并以此重建无雾图像，然而，不准确的透射图往往会对去雾效果产生不利影响。此外，ENGIN等^[11]提出一种基于循环生成对抗网络（Cycle Generative Adversarial Network，CycleGAN）的改进去雾网络Cycle-dehaze，该网络通过增加循环感知一致性损失以及循环一致性损失来增强用于单图像去雾的CycleGAN架构。YANG等^[12]将与雾度相关的先验学习引入到深度学习网络中，所提算法结合了传统的基于先验的去雾方法和深度学习方法的优点。LI^[13]提出一种轻量级的CNN网络AOD-Net，该网络可以直接生成无雾图像，这种端到端设计使得研究人员可以很容易地将AOD-Net嵌入到其他深度学习模型中。ZHANG等^[14]提出一个双分支卷积神经网络，该网络首先提取基本特征和恢复特征，其次将这些特征通过递归门模块进行融合以获得超分辨率的清晰特征，从而提高了生成图像的质量。

尽管上述方法大多取得了较好的性能指标结果，但是普遍依赖于成对的数据集，这就意味着对于每一个有雾图像，都需要一个与之相对应的无雾图像。然而，由于光照强度和对比度在不断地发生变化，同时收集同一场景下的有雾图像与无雾图像时成本较高，难度较大。因此，需要探索一种不依赖于成对数据集训练的图像去雾算法。

本文选用CycleGAN^[15]作为基础网络，该网络于2017年被提出，之后广泛应用于图像修复、风格迁移等领域^[16]。近年来，有很多优秀的去雾算法都使用CycleGAN及其衍生网络^[17]，相较传统的神经网络，CycleGAN最大的优势在于不需要成对的数据集进行训练，大幅降低了对数据集的要求。但是，CycleGAN依然存在去雾后图像失真的问题。为此，本文在CycleGAN的基础上对网络的损失函数进行改进，通过引入颜色损失函数使去雾后的图像与原始无雾图像具有相同的颜色分布，此外，引入特征损失函数，以保留图像的细节特征，提高去雾后图像的质量。

1 网络结构 1.1 生成对抗网络

GAN采用博弈论中二人零和博弈的思想，网络包括生成器和判别器，采用对抗训练的方式进行训练。其中，生成器根据输入图像生成一张类似训练数据的虚假图像以“骗”过判别器，而判别器的作用是区分真实数据和所生成的虚假数据，并将其判断结果反馈给生成器，生成器根据结果再进行训练，以提高生成更真实图片的能力。通过上述过程，生成器与判别器之间会达到一个均衡的状态，GAN的目标函数可以表示为：

$ \begin{array}{*{20}{l}} {{\rm{minmax}}\;V({\rm{D}},{\rm{G}}) = {E_{x \sim {P_{{\rm{data}}\left( x \right)}}}}[{\rm{lg}}\;{\rm{D}}(x)] + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{E_{z \sim P\left( z \right)}}[{\rm{lg}}(1 - {\rm{D}}({\rm{G}}(z)))]} \end{array} $

(1)

其中：x是真实的输入数据；$ {P}_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}\left(x\right)} $表示真实数据的分布；z表示随机噪声；$ P\left(z\right) $表示生成网络的分布。该目标函数表示：对于判别器D，希望它能够准确分辨出生成器生成的虚假图片，即希望$ \mathrm{D}\left(\mathrm{G}\right(z\left)\right) $接近于0，此时目标函数的值最小；对于生成器G，希望它生成的每张图片都可以骗过判别器，即希望$ \mathrm{D}\left(\mathrm{G}\right(z\left)\right) $接近于1，此时目标函数的值最大。当$ \mathrm{D}\left(\mathrm{G}\right(z\left)\right)=0.5 $时，就达到了平衡状态。

1.2 循环生成对抗网络

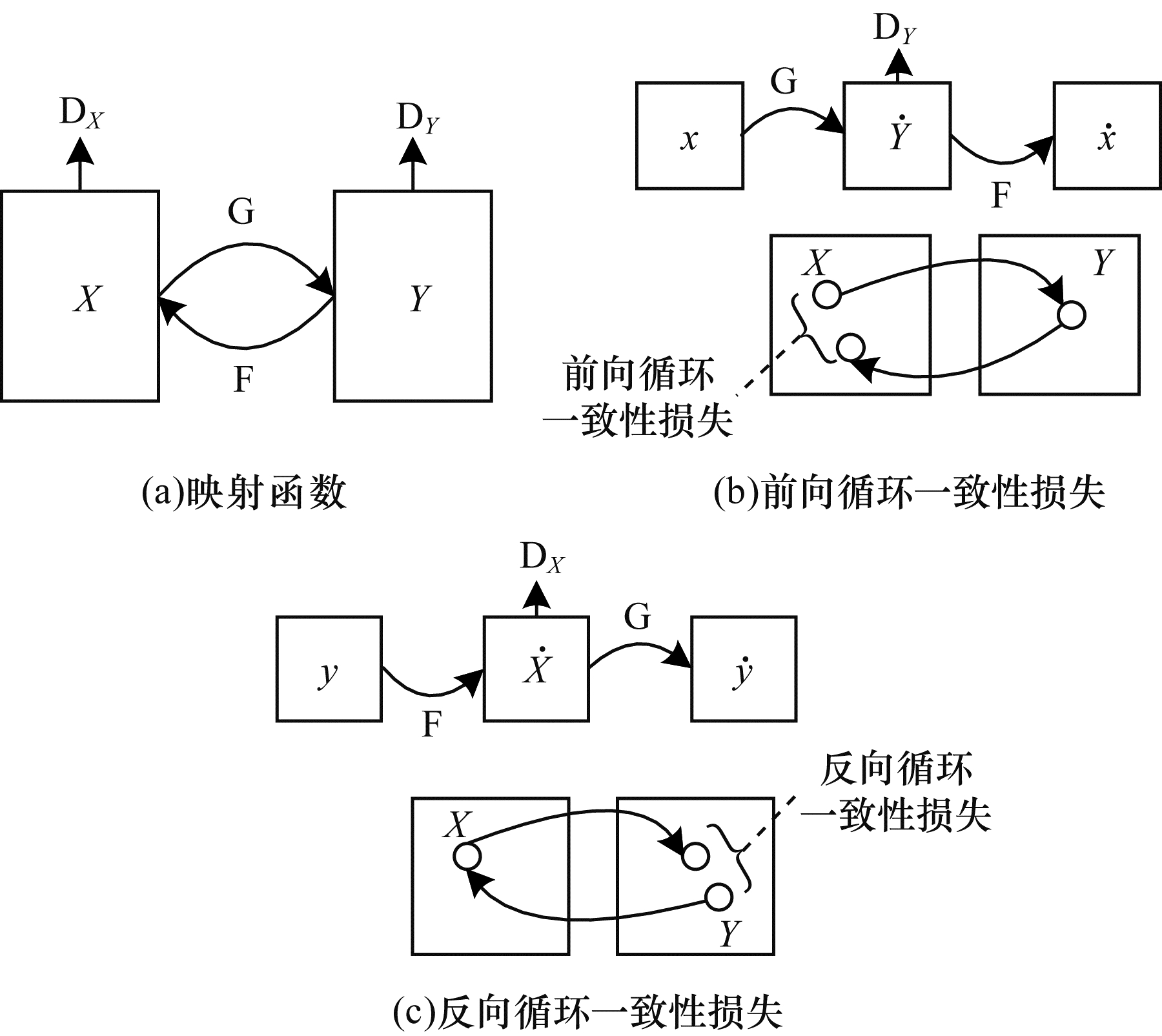
CycleGAN的目的是实现X域图像数据与Y域图像数据的相互转换。如图 1（a）所示，CycleGAN包含2个映射函数，分别是$ \mathrm{G}:X\to Y $和$ \mathrm{F}:Y\to X $，同时还包括$ {\mathrm{D}}_{Y} $和$ {\mathrm{D}}_{X} $这2个判别器。$ {\mathrm{D}}_{Y} $输出的判别结果会激励生成器G将X向Y域中转换，同样，$ {\mathrm{D}}_{X} $输出的判别结果会激励生成器F将Y向X域中转换。此外，为了保证图像转换时的一致性，避免出现X域中的所有图片都被映射到Y域中同一张图片的情况，CycleGAN中引入2个循环一致性损失，所谓循环一致性损失，指的是图像从源域转换到目标域后，同样也可以从目标域返回到源域。图 1（b）所示为前向循环一致性损失，即图像从X域经过生成器G后，再经过生成器F仍然可以转换到源域，可表示为：$ x\to \mathrm{G}\left(X\right)\to \mathrm{F}\left(\mathrm{G}\right(X\left)\right)\approx x $。同理，图 1（c）所示为反向循环一致性损失，即Y域中的图片经生成器转换到X域后，再经过生成器G仍然可以转换到源域，可以表示为：$ y\to \mathrm{F}\left(Y\right)\to \mathrm{G}\left(\mathrm{F}\right(Y\left)\right)\approx y $。

1.3 对抗损失

CycleGAN中引入了2个对抗损失，对于映射函数$ \mathrm{G}:X\to Y $以及判别器$ {\mathrm{D}}_{Y} $，有：

$ \begin{array}{*{20}{l}} {{L_{{\rm{GAN}}}}({\rm{G}},{{\rm{D}}_Y},X,Y){ = _{y \sim {P_{{\rm{data}}\left( y \right)}}}}[{\rm{lg}}\;{{\rm{D}}_Y}(y)] + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\;_{x \sim {P_{{\rm{data}}\left( x \right)}}}}[{\rm{lg}}(1 - {{\rm{D}}_Y}({\rm{G}}(x)))]} \end{array}$

(2)

其中：$ {P}_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}\left(x\right)} $表示X域的样本分布；$ {P}_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}\left(y\right)} $表示Y域的样本分布。式（2）表示当生成器G试图让其生成的图像与Y域中的图像尽可能相似时，判别器D也在试着将真实图片与生成的虚假图片区分开，这样，生成器与判别器就形成了对抗关系，因此，可以表示为$ \mathrm{m}\mathrm{i}{\mathrm{n}}_{\mathrm{G}}\;\mathrm{m}\mathrm{a}{\mathrm{x}}_{{\mathrm{D}}_{Y}}\;{L}_{\mathrm{G}\mathrm{A}\mathrm{N}}(\mathrm{G}, {\mathrm{D}}_{Y}, X, Y) $。

同理，另一个映射$ \mathrm{F}:Y\to X $和它的判别器$ {\mathrm{D}}_{X} $也是如此，可以表示为：$ \mathrm{m}\mathrm{i}{\mathrm{n}}_{\mathrm{F}}\;\mathrm{m}\mathrm{a}{\mathrm{x}}_{{\mathrm{D}}_{X}}\;{L}_{\mathrm{G}\mathrm{A}\mathrm{N}}(\mathrm{F}, {\mathrm{D}}_{X}, Y, X) $。

1.4 循环一致性损失

从理论上来讲，当G和F是随机函数时，1.3节中的对抗损失可以使生成器G和F分别产生与目标域Y和X相同分布的输出。然而，仅使用对抗损失可能出现图像在转换时无法保留其内容、结构等信息的问题，CycleGAN通过引入循环一致性损失来解决该问题。如图 1（b）所示，对于X域中的每一张图像x，图像的循环转换都应该能够将x还原成原始图像，即$ x\to \mathrm{G}\left(X\right)\to \mathrm{F}\left(\mathrm{G}\right(X\left)\right)\approx x $，同样对Y域中的每一个图像y来说，G和F也要满足反向循环一致性条件：$ y\to \mathrm{F}\left(Y\right)\to \mathrm{G}\left(\mathrm{F}\right(Y\left)\right)\approx y $。循环一致性损失定义如下：

$ \begin{array}{*{20}{l}} {{L_{{\rm{cycle}}}}({\rm{G}},{\rm{F}}){ = _{x \sim {P_{{\rm{data}}\left( x \right)}}}}[||{\rm{F}}({\rm{G}}\left( x \right)) - x|{|_1}] + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\;_{y \sim {P_{{\rm{data}}\left( y \right)}}}}[||{\rm{G}}({\rm{F}}\left( y \right)) - y|{|_1}]} \end{array} $

(3)

其中：$ \mathrm{G}\left(x\right) $和$ \mathrm{F}\left(y\right) $是前向生成器和反向生成器；x是属于X域的图像；y是属于Y域的图像；$ \mathrm{F}\left(\mathrm{G}\right(x\left)\right) $和$ \mathrm{G}\left(\mathrm{F}\right(y\left)\right) $是重新构建的图像。

2 CycleGAN改进

CycleGAN使用对抗损失函数使得判别器拥有判断一张图片是否具有目标域风格的能力，同时，使用循环一致性损失函数来确保重构图像与原始图像大致相似。但是，在CycleGAN中，去雾前后图像颜色失真，此外，图像在特定域转换时由无关域随机变化导致生成器不能很好地保留图像特征。本文引入颜色损失和特征损失来解决上述问题。

2.1 颜色损失函数

通常来说，有雾的图像缺乏亮度与对比度，因此，受文献[18]的启发，本文引入颜色损失函数来最小化无雾图像与重构的无雾图像之间的误差，以此强制生成器生成与无雾图像具有相同颜色分布的图像。颜色损失函数定义如下：

$ {L_{{\rm{color}}}} = \sum\limits_p \angle ({\rm{G}}{({\rm{F}}\left( y \right))_p},{y_p}) $

(4)

其中：$ {\left(\right)}_{p} $表示一个像素点；$ \mathrm{\angle }(, ) $是将RGB颜色作为3D矢量并计算2种颜色之间角度的运算符；y是Y域中的无雾图像；$ \mathrm{G}\left(\mathrm{F}\right(y\left)\right) $是重构的无雾图像。通过优化重构图像与原始无雾图像中每个像素点的误差和，可以解决图像转换过程中颜色失真的问题。

2.2 特征损失函数

如图 2所示，已知CycleGAN中有生成器映射$ \mathrm{G}:X\to Y $，表示生成器G将X域中的图像转换为Y域中的图像，那么当向G中输入原本就是Y域的图像y时，希望$ \mathrm{G}\left(y\right) $与原始的y图像尽可能地接近。因此，采用文献[19]的思想，本文在2个生成器上分别添加一个恒等映射，即$ \mathrm{G}:Y\to Y $和$ \mathrm{F}:X\to X $，将此映射中的损失称为特征损失。在加入了特征损失后，生成器G在原有输入的基础上增加了Y域图像的输入，生成器F也添加了X域图像的输入。使用L1损失函数对原图像和生成的图像进行优化，可以确保2个生成器在生成目标域图像时能获取目标域中图像的特征，从而更好地还原原始图像的细节特征，提高生成图像的质量。

特征损失函数定义如下：

$\begin{array}{*{20}{l}} {{L_{{\rm{idt}}}}({\rm{G}},{\rm{F}}){ = _{x \sim {P_{{\rm{data}}\left( x \right)}}}}[||{\rm{F}}(x) - x|{|_1}] + }\\ {\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\;_{y \sim {P_{{\rm{data}}\left( y \right)}}}}[||{\rm{G}}(y) - y|{|_1}]} \end{array} $

(5)

其中：x是属于X域的图像；y是属于Y域的图像；$ {P}_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}\left(x\right)} $表示X域的样本分布；$ {P}_{\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}\left(y\right)} $表示Y域的样本分布；$ \mathrm{G}\left(y\right) $与$ \mathrm{F}\left(x\right) $分别是添加了Y域图像输入和X域图像输入的生成器。

改进之后的网络总损失函数可以表示为：

$ \begin{array}{l}L(\mathrm{G}, \mathrm{F}, {\mathrm{D}}_{X}, {\mathrm{D}}_{Y})={L}_{\mathrm{G}\mathrm{A}\mathrm{N}}(\mathrm{G}, {\mathrm{D}}_{Y}, X, Y)+\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;{L}_{\mathrm{G}\mathrm{A}\mathrm{N}}(\mathrm{F}, {\mathrm{D}}_{X}, Y, X)+{L}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{r}}+\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \lambda {L}_{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}}(\mathrm{G}, \mathrm{F})+\mu {L}_{\mathrm{i}\mathrm{d}\mathrm{t}}(\mathrm{G}, \mathrm{F})\end{array} $

(6)

其中：$ {L}_{\mathrm{G}\mathrm{A}\mathrm{N}} $是对抗损失；$ {L}_{\mathrm{c}\mathrm{o}\mathrm{l}\mathrm{o}\mathrm{r}} $是颜色损失；$ {L}_{\mathrm{c}\mathrm{y}\mathrm{c}\mathrm{l}\mathrm{e}} $是循环一致性损失；$ {L}_{\mathrm{i}\mathrm{d}\mathrm{t}} $是特征损失；$ \lambda $和$ \mu $分别是循环一致性损失与特征损失的权值参数。$ \lambda $的值选用CycleGAN中的默认值10，$ \mu $的值会影响网络的性能表现，下文将对此进行讨论。

3 实验结果与分析 3.1 实验过程

本文实验采用NYU-depth-v2数据集^[20]，其为图像去雾领域常用的数据集，共包含1 449张有雾图与无雾图，NYU数据集规模较大，本文选择在该数据集上进行训练和测试。首先，将数据集按照一定比例随机划分为训练集和测试集，训练集由trainA和trainB这2个部分组成，trainA中存放有雾图像，trainB中存放无雾图像，训练集中不包含测试集图像的任何信息。同时，在训练之前将训练图像压缩至286×286像素，以适配网络要求的输入尺寸。

实验所用环境为：Ubuntu16.04系统，CPU为Intel^® Xeon^® E5-2678 v3 @2.50 GHz，62 GB内存，GPU为一块NVIDIA 2080Ti 11 GB显卡，使用深度学习框架Pytorch 1.4.0，编程语言为Python3.6。

本次实验使用batch size为1的Adam优化器。网络共迭代200个epoch，在前100个epoch中，网络的学习率保持0.000 2不变，在之后的100个epoch中学习率线性衰减至0。

3.2 评价指标

本文采用图像去雾领域常用的性能指标对实验结果进行评价，包括结构相似性指数（Structural Similarity Index，SSIM）^[21-22]、峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）。

SSIM通过比较参考图像与待评图像的亮度、对比度和结构，以计算2幅图像之间的结构相似性，该值越大，说明图像失真越小，生成图像的质量越好。SSIM效果可靠且具有说服力，因此，在图像去雾领域得到广泛应用^[23]。

PSNR通过计算待评图像与参考图像之间各个像素点的误差之和来评价一个算法的性能，该值越高，表明图像失真越小，重建方法越有效。

3.3 结果分析

本文实验主要包括3个部分：首先，通过客观数据证明本文算法相较其他算法的优越性；其次，列举消融实验和对比实验的结果，证明本文所提改进方法的有效性；最后，讨论不同的特征损失函数权值$ \mu $对网络去雾能力的影响，并给出$ \mu $值的选取建议。

3.3.1 客观评价

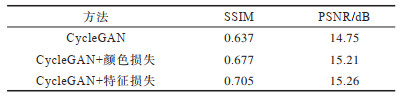
使用图像去雾领域常用的指标SSIM、PSNR进行比较，消融实验结果如表 1所示，从表 1可以看出，相较原始CycleGAN，在添加了颜色损失函数和特征损失函数之后，结构相似性指数SSIM分别提高约4和7个百分点，峰值信噪比PSNR分别提高约3.1和3.5个百分点，这证明了本文所提改进方法的有效性。

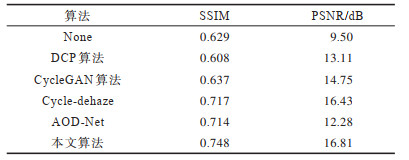
使用不同的去雾算法在测试集上进行图像去雾，性能指标结果如表 2所示。从表 2可以看出，使用DCP算法进行去雾后虽然提高了图像的平均PSNR值，但其平均SSIM值反而下降，使用另外3种算法去雾后图像的性能指标有不同程度的提升，但是本文算法依然取得了最高的平均SSIM值和PSNR值。

3.3.2 主观评价

本节首先通过消融实验证明本文引入的颜色损失和特征损失函数的有效性，随后通过对比实验验证本文改进后算法的优势。加入颜色损失函数的实验结果如图 3所示，其中，左图为未添加颜色损失函数的结果，右图为加入颜色损失函数后的结果，从图中的方框处可以看出，引入颜色损失函数之前图片中桌子一侧由于颜色失真引起了过度曝光的问题，而加入颜色损失后解决了该问题。引入特征损失函数的实验结果如图 4所示，从左到右依次是未添加特征损失函数处理结果、引入特征损失函数处理结果及对应的原始图像。可以看出，加入特征损失后能更好地还原方框中物体的细节特征，生成的图像更接近原始图像。

将本文算法与DCP算法、CycleGAN算法、AOD-Net算法，以及基于CycleGAN的去雾算法Cycle-dehaze进行比较，从实验结果中随机抽取5张图片，结果如图 5所示。从前2张图片可以看出，本文算法在去雾能力上优于3种对比算法，去雾效果更好。从后3张图片可以看出，DCP算法去雾后存在严重的颜色失真问题，而其余3种算法去雾后图片虽然在颜色失真问题上优于DCP算法，但是去雾效果依然没有本文算法明显。因此，从主观结果和客观结果上可以得出，本文算法可以更好地还原图像的细节特征及颜色信息，生成的图像更接近原始图像。

3.3.3 $ \mu $值对网络性能的影响

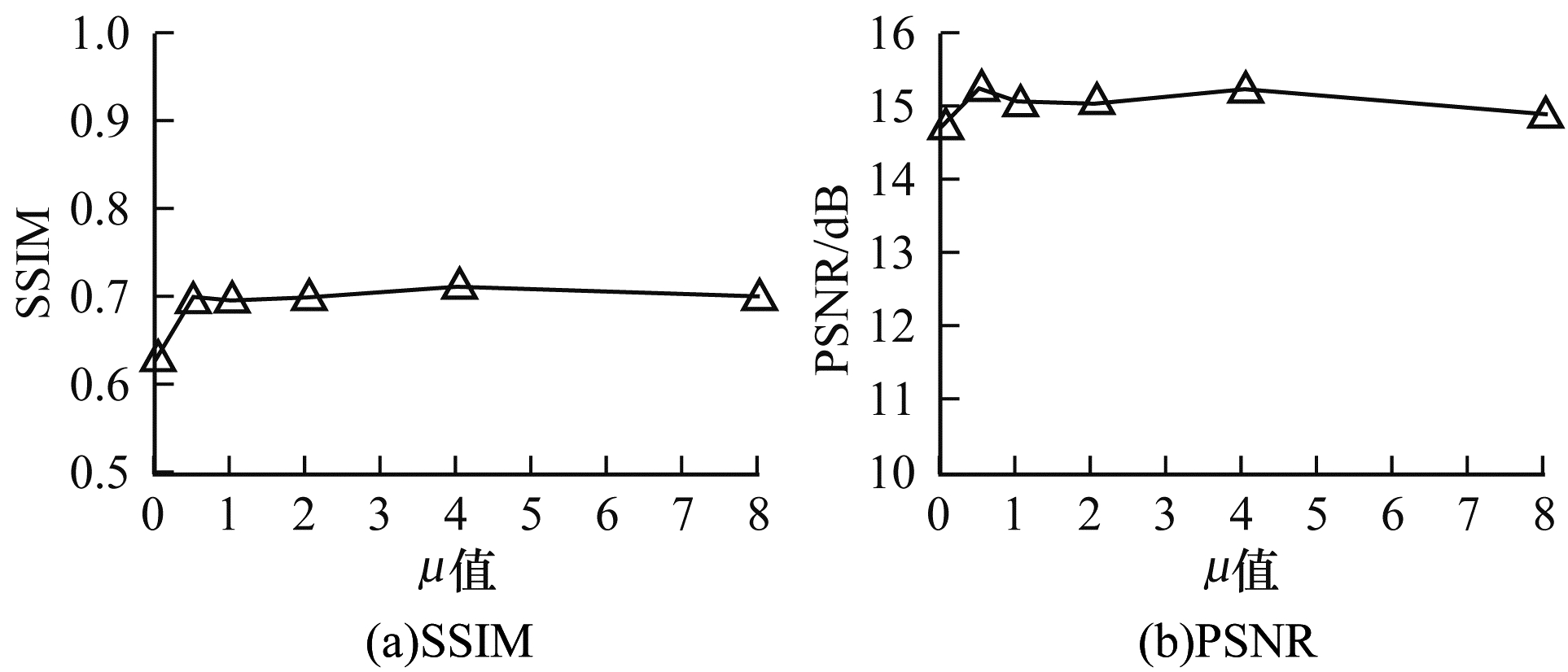
在证明引入特征损失函数可以有效提高网络去雾性能之后，本文进一步探究不同的特征损失权重参数$ \mu $值对网络性能的影响，分别测试$ \mu =\mathrm{0, 0.5, 1}, \mathrm{2, 4}, 8 $时网络在测试集上的性能指标，结果如图 6所示。从图 6（a）可以看出，当$ \mu $取0.5~8时，网络的SSIM指标在一个很小的范围内波动，从图 6（b）可以看出，当$ \mu $取0.5左右时，网络具有最好的PSNR指标，同时在训练过程中观察到，当$ \mu $的取值大于2时，损失函数曲线收敛情况并不好。因此，根据该实验结果，本文建议将$ \mu $值设置在0.5左右，以使网络拥有最佳的去雾性能。

4 结束语

本文提出一种基于改进循环生成对抗网络的图像去雾算法，该算法通过引入颜色损失和特征损失来解决网络去雾过程中存在的颜色失真问题，能更好地保留原始图像的细节特征，使得去雾效果更佳。实验结果表明，该算法的去雾能力优于AOD-Net、Cycle-dehaze等算法。下一步将使用Ghost模块^[24]替代卷积块并结合注意力机制，在保证去雾图像质量的同时减少网络参数，提高去雾的效率，从而将本文算法应用于视频去雾领域。