2. 丽水学院 工学院,浙江 丽水 323000
2. School of Engineering, Lishui University, Lishui, Zhejiang 323000, China
开放科学(资源服务)标志码(OSID):
三维点云模型研究是计算机图形学、计算机视觉与模式识别领域共同关注的热点话题之一。二维图像丢失了现实世界中2个或多个物体间的深度信息,不适用于需要深度信息和定位信息的领域,如机器人、自主驾驶等。为了用深度信息捕捉三维世界,早期常见的方法是使用立体视觉技术,即用2个或更多校准的数码相机来提取三维信息。点云是围绕场景中物体曲面采样的三维数据点集,可以由点的X、Y、Z坐标表示,也可以加入诸如曲面法线、RGB值等附加特性,可见点云是一种用于表示三维几何体的基础数据结构。
保证特征旋转不变是计算机视觉与模式识别领域的重要技术之一,例如在处理图像时提取的特征要保证旋转不变。不同于图像的二维平面结构,点云的结构为三维空间,进行点云数据处理要保证其绕X、Y、Z这3个坐标轴旋转时所提取的特征不变,因此点云空间旋转不变性的实现比二维图像实现旋转不变性更具挑战。点云数据是一个包含三维坐标信息的无序点集合,对数据顺序不敏感,相同的一个点云数据模型完全可以有多种不同的存储顺序,这意味着处理点云数据时需要保持数据的不同排列不变性,即点云的置换不变性。处理点云无序性的一般方法包括用对称函数来保证置换不变性、将无序的数据进行重新排序及对数据的所有排列进行数据增强后使用RNN模型。
本文提出一种基于亲疏度矩阵的点云置换不变特征提取方法,在M-Conv模型第1层输入时将点坐标映射到曲率特征空间以实现空间旋转不变性。基于欧式内积构建K邻域内的亲疏度矩阵,以反映点之间的亲疏关系。根据亲疏度矩阵计算得到变换矩阵,对输入的数据进行变换以实现置换不变性。此外,采用代数计算的方式获取变换矩阵,提高模型训练的效率,并在常规卷积神经网络的基础上,设计一套用于处理点云空间旋转不变性和置换不变性问题的框架。
1 相关工作针对点云空间旋转不变性和置换不变性问题,研究人员已提出诸多方法,总体而言可以分为基于多视图的方法[1-3]、基于体素的方法[4-5]和基于点的深度学习方法。基于多视图的方法将点云投影到多视图表示来学习特征,基于体素的方法将点云放入体素网格中进行处理,但这些方法的计算量和内存占用非常庞大,无法很好地应用到密集的3D数据中。基于点的深度学习方法包括点对点MLP网络[6-8]、基于卷积的网络[9-11]、基于图的网络[12-13]及基于数据索引的网络[14-15],这些方法会对点进行特征学习。除此之外,还有一些方法如基于径向基函数的DeepRBFNet[16]、将胶囊网络引入到点云中的3DPointCapsNet[17]、使用自注意力模块的RMFP-DNN[18]等。
1.1 点云空间旋转不变性针对点云空间旋转不变性问题,PointNet[6]通过训练T-Net得到K×K矩阵,并对输入进行空间对齐以保证空间旋转不变性。文献[9]提出3D球面卷积神经网络Spherical CNN来学习3D形状的旋转不变性,其以多值球面函数为输入,通过在球形谐波域中使用锚点对频谱进行参数化来获得局部卷积滤波器。借鉴于Spherical CNN,文献[10]介绍了构建球面CNN的基本要素,其卷积定义为在球形互相关上使用通用快速傅里叶变换算法实现。SRINet[19]首先投影1个点云以获得旋转不变表示,然后利用基于PointNet的主干来提取全局特征,并利用基于图的聚合来提取局部特征,但先进行投影的方式会大幅增加计算量。文献[20]提出张量场网络,将点卷积运算定义为可学习的径向函数和球谐函数的乘积,其局部等价于点的3D旋转、平移和置换。SPHNet[21]通过在体积函数的卷积过程中合并球形谐波核来实现旋转不变性。ConvPoint[22]将卷积核分为空间和特征两部分,从单位球体中随机选择空间部分的位置,并使其通过简单的MLP学习加权函数。这些基于球形卷积的方法同样会增加计算量,其学习方式也无法很好地被应用于非监督性方法中。本文方法将点坐标映射到曲率特征空间,以实现空间旋转不变性。
1.2 点云置换不变性关于如何解决点云置换不变性问题,PointNet使用最大池化对称函数来提取数据的特征,但基于最大池化的方法忽略了点之间的局部结构信息。QI等[7]在PointNet的基础上提出层次网络PointNet++来捕获每个点附近的几何结构,取得了更好的结果。ZAHEER等[8]从理论上证明实现置换不变性的关键是对所有表示求和的应用进行非线性变换,他们还为包括形状分类在内的各种应用设计了一种基本架构DeepSets。PointCNN[11]通过学习的方式获得一个变换矩阵,对无序的数据进行变换使之转变为有序输入。文献[17]提出一种无监督的自动编码器3DPointCapsNet用于3D点云的通用表示,使用逐点MLP和卷积层学习点独立特征,并使用多个最大池化层提取全局特征。文献[23]提出的RS-CNN以RS-Conv为核心层,将某个点周围的局部点子集作为输入,然后通过学习映射并使用MLP进行卷积,将低级关系(例如欧氏距离和相对位置)转换为局部子集中点之间的高级关系来获得变换矩阵。PointConv[24]中的卷积定义为蒙特卡洛估计,这是一个关于重要性采样的连续3D卷积,卷积核由权重函数(通过MLP层学习)和密度函数(通过核化密度估计和MLP层学习)组成。WU等[25]提出的RCNet利用标准的RNN和2D CNN来构建用于3D点云处理的置换不变网络,先将点云划分为平行波束,并沿特定维度进行分类,然后将每个波束送入共享的RNN中进行处理,再将所学习的特征进一步反馈并送到2D CNN中进行分层特征聚合。本文方法将基于点与点之间的欧式内积构建亲疏度矩阵,计算并得到相应的变换矩阵,对输入进行变换,使之从无序状态转变为有序状态。
2 基于亲疏度矩阵的M-Conv本文将基于点与点之间的欧式内积构建K邻域内的亲疏度矩阵,并计算亲疏度矩阵特征值,对其进行排序后将对应的特征向量矩阵作为变换矩阵
本文方法的输入是一系列点与特征的集合
| $ {{\boldsymbol{ F}}}_{2}={\mathrm{C}}{\mathrm{o}}{\mathrm{n}}{\mathrm{v}}\left({\boldsymbol{ Q}}\text{,}{\boldsymbol{ M}}\times {{\boldsymbol{ F}}}_{1}\right) $ | (1) |
其中:
|
Download:
|
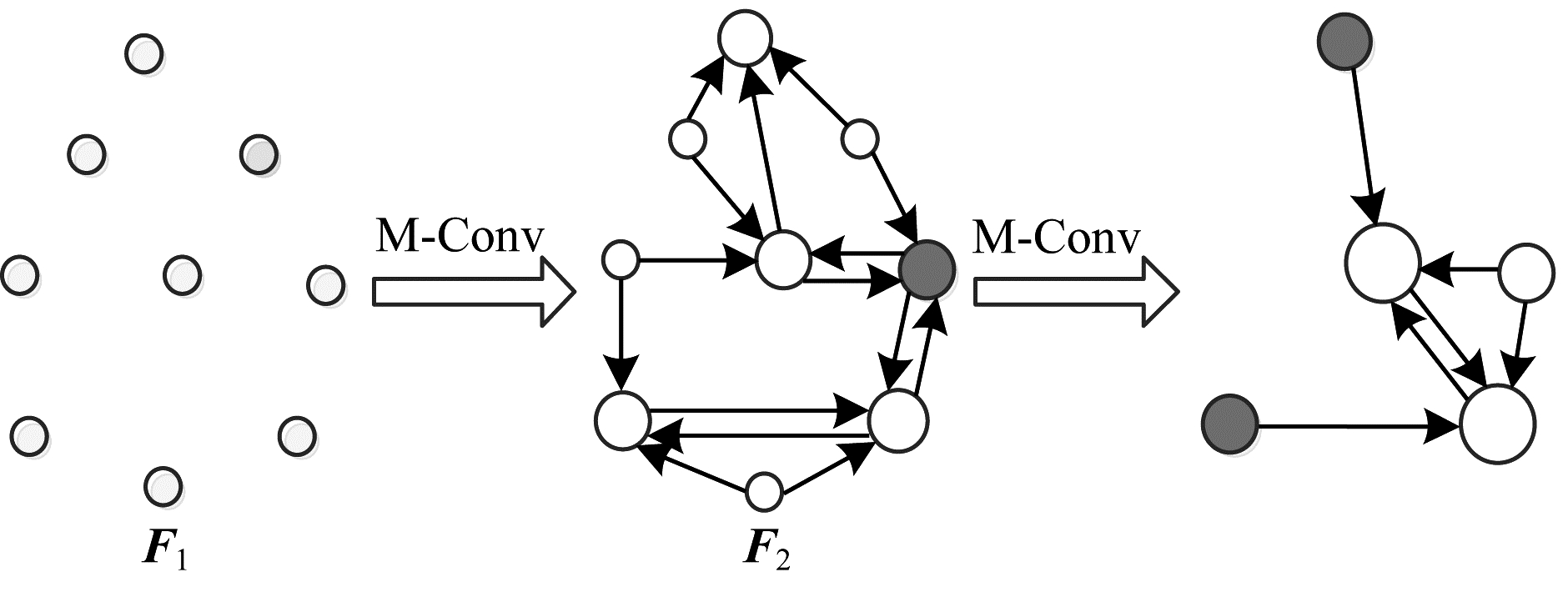
| 图 1 M-Conv分层卷积 Fig. 1 Hierarchical convolution of M-Conv | |
通过M-Conv的处理,代表点{
为保证置换不变性的实现,本文通过找出与代表点最近的K个点形成K邻域,根据K邻域内点的相对关系构建1个K
| $ \left[\begin{array}{cccccc}(K-1){p}_{1}^{2}& \cdots & -2{p}_{1}*{p}_{i}& -2{p}_{1}*{p}_{j}& \cdots & -2{p}_{1}*{p}_{k}\\ -2{p}_{2}*{p}_{1}& \cdots & -2{p}_{2}*{p}_{i}& -2{p}_{2}*{p}_{j}& \cdots & -2{p}_{2}*{p}_{k}\\ ⋮& & ⋮& ⋮& & ⋮\\ -2{p}_{i}*{p}_{1}& \cdots & (K-1){p}_{i}^{2}& -2{p}_{i}*{p}_{j}& \cdots & -2{p}_{i}*{p}_{K}\\ -2{p}_{j}*{p}_{1}& \cdots & -2{p}_{j}*{p}_{i}& (K-1){p}_{j}^{2}& \cdots & -2{p}_{j}*{p}_{K}\\ ⋮& & ⋮& ⋮& & ⋮\\ -2{p}_{K}*{p}_{1}& \cdots & -2{p}_{K}*{p}_{i}& -2{p}_{K}*{p}_{j}& \cdots & (K-1){p}_{K}^{2}\end{array}\right] $ | (2) |
交换点与点之间的存储顺序是点云无序性的重要体现,但并不改变其本质归属。2.2节基于欧式内积构建了K
| $ {{\boldsymbol{ L}}}^{\text{'}}x=\lambda x $ | (3) |
计算矩阵
| $ {\boldsymbol{ M}}=\left[{{\boldsymbol{ x}}}_{2}\text{,}{{\boldsymbol{ x}}}_{3}\text{,}{{\boldsymbol{ x}}}_{1}\right] $ | (4) |
根据亲疏度矩阵计算得到的变换矩阵
在式(2)中交换
| $ \left[\begin{array}{cccccc}(K-1){p}_{1}^{2}& \cdots & -2{p}_{1}*{p}_{j}& -2{p}_{1}*{p}_{i}& \cdots & -2{p}_{1}*{p}_{k}\\ -2{p}_{2}*{p}_{1}& \cdots & -2{p}_{2}*{p}_{j}& -2{p}_{2}*{p}_{i}& \cdots & -2{p}_{2}*{p}_{k}\\ ⋮& & ⋮& ⋮& & ⋮\\ -2{p}_{j}*{p}_{1}& \cdots & (K-1){p}_{j}^{2}& -2{p}_{j}*{p}_{i}& \cdots & -2{p}_{j}*{p}_{K}\\ -2{p}_{i}*{p}_{1}& \cdots & -2{p}_{i}*{p}_{j}& (K-1){p}_{i}^{2}& \cdots & -2{p}_{i}*{p}_{K}\\ ⋮& & ⋮& ⋮& & ⋮\\ -2{p}_{K}*{p}_{1}& \cdots & -2{p}_{K}*{p}_{j}& -2{p}_{K}*{p}_{i}& \cdots & (K-1){p}_{K}^{2}\end{array}\right] $ | (5) |
交换
| $ {{\boldsymbol{ L}}}_{1}\to {{\boldsymbol{ L}}}_{1}^{\text{'}}\to {{\boldsymbol{ L}}}_{1}^{{\boldsymbol{ \text{'}}}{\boldsymbol{ \text{'}}}}={\boldsymbol{ L}} $ | (6) |
M-Conv是本文处理点云数据方法的核心操作。本小节将介绍M-Conv操作的整体算法流程,并解释其基本原理。
算法1 M-Conv操作
输入
输出
1.
2.
3.
4.
5.
6.
在算法1中:
| $ {\boldsymbol{ F}}=M-{\mathrm{C}}{\mathrm{o}}{\mathrm{n}}{\mathrm{v}}({\boldsymbol{ Q}}\text{,}p\text{,}{\boldsymbol{ P}}\text{,}{{\boldsymbol{ F}}}_{\bf{p}}) $ | (7) |
进一步可得:
| $ \begin{array}{l}{\boldsymbol{ F}}={\mathrm{C}}{\mathrm{o}}{\mathrm{n}}{\mathrm{v}}({\boldsymbol{ Q}}\text{,}{\mathrm{C}}{\mathrm{a}}{\mathrm{l}}\_{\mathrm{M}}({\mathrm{C}}{\mathrm{a}}{\mathrm{l}}\_{\mathrm{L}}({\boldsymbol{ P}}-p)){\mathrm{ }}\times \\ \left[{\mathrm{M}}{\mathrm{L}}{{\mathrm{P}}}_{\mathtt{α}}\right({\boldsymbol{ P}}-p)\text{,}{{\boldsymbol{ F}}}_{\bf{p}}])\end{array} $ | (8) |
| $ {\boldsymbol{ F}}={\mathrm{C}}{\mathrm{o}}{\mathrm{n}}{\mathrm{v}}({\boldsymbol{ Q}}\text{,}{\mathrm{M}}{\mathrm{L}}{{\mathrm{P}}}_{\mathtt{α}}({\mathrm{C}}{\mathrm{a}}{\mathrm{l}}\_{\mathrm{C}}({\boldsymbol{ P}}-p)\left)\right) $ | (9) |
其中:Cal_C()是将点坐标映射到曲率特征空间的操作,详细过程请参考2.6节细节补充。
算法1的第3行~第5行是M-Conv的关键操作,能够保证其实现置换不变的特性。M-Conv是在局部区域工作的,其输出不需要依赖于
|
Download:
|
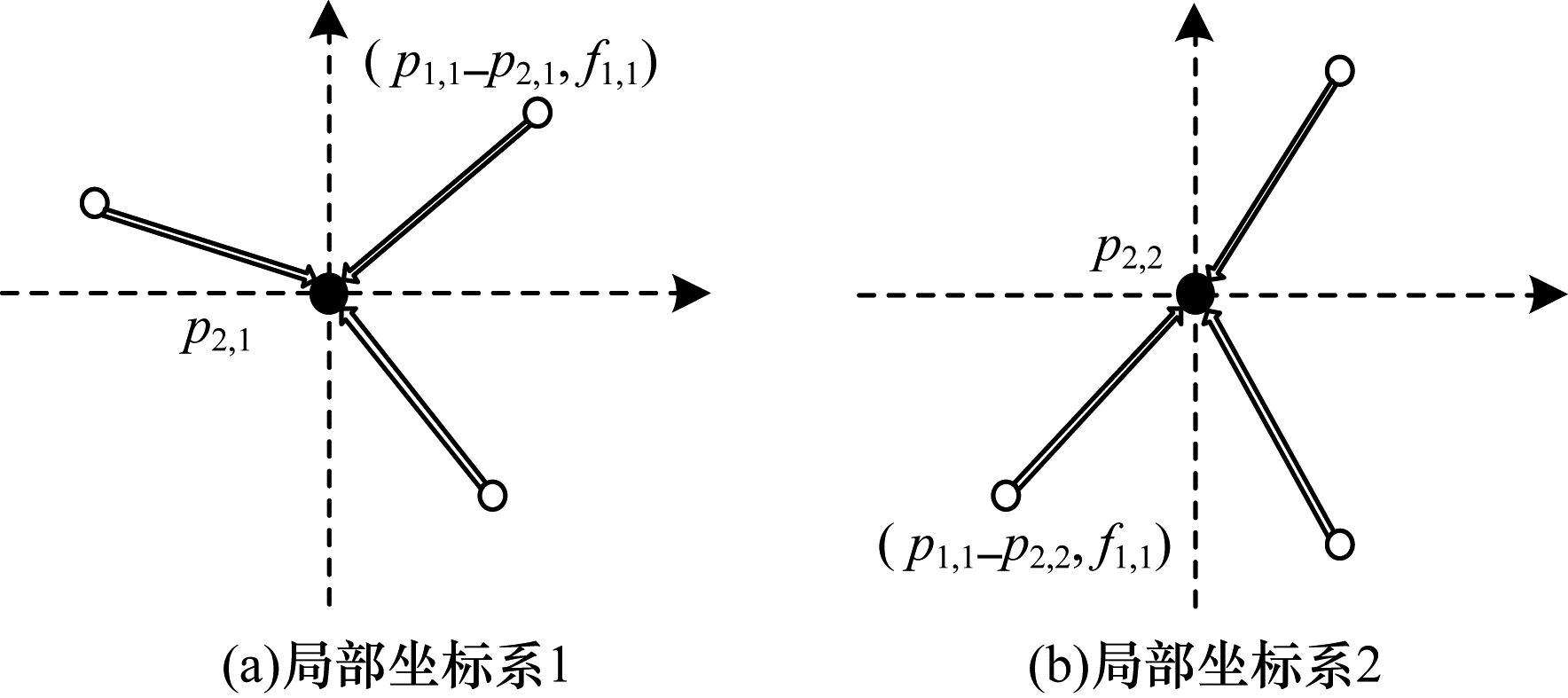
| 图 2 局部坐标系建立 Fig. 2 Establishment of local coordinate system | |
本文参考PointCNN,通过逐点
基于网格的卷积神经网络的Conv层和M-Conv层在特征提取的局部区域(K
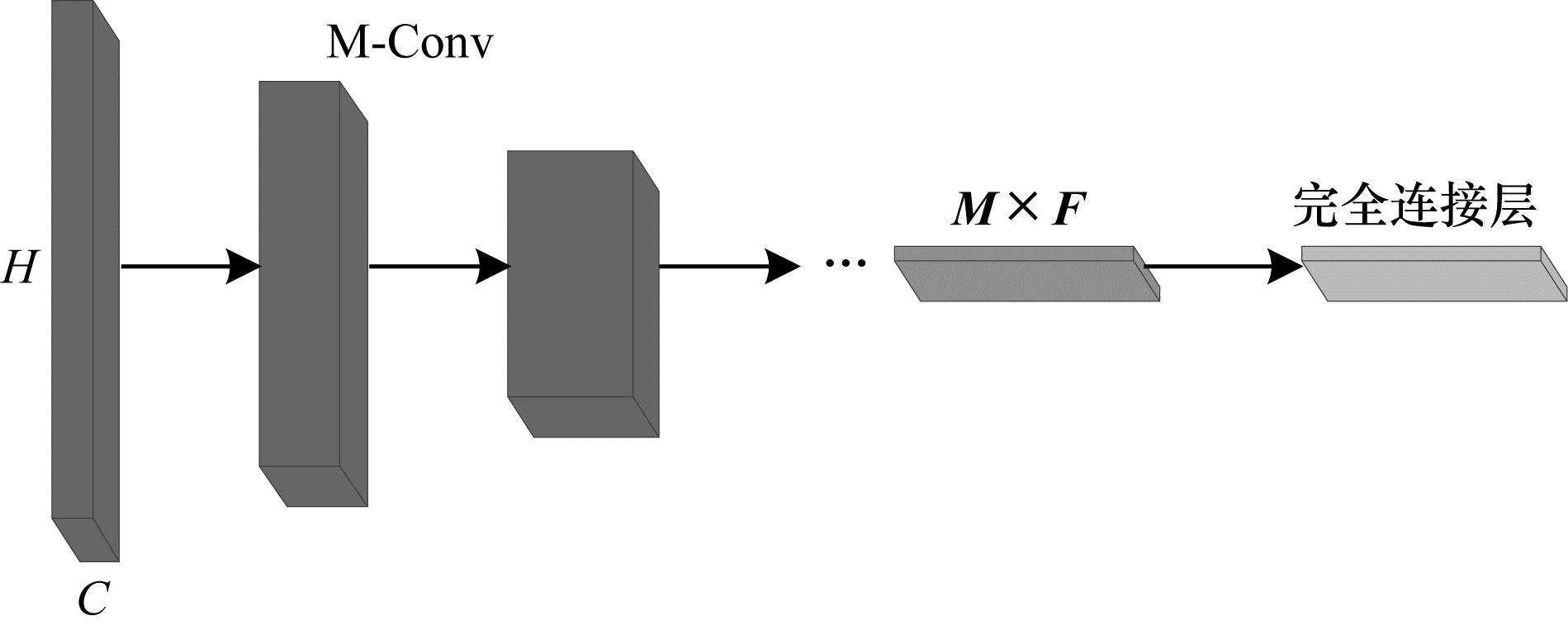
图 3所示为一个简单的由M-Conv组成的网络模型,其中:H代表点数量;C是输出特征通道数量。该模型能够将输入点(附带有或不附带有特征)转换为更少的代表点,每个代表点都将聚合来自上一层自身邻域点的特征,因此自身所附带的特征会变得更加丰富,感受野也逐步扩大。由最后一层M-Conv处理得到的特征
|
Download:
|
| 图 3 M-Conv网络模型的结构 Fig. 3 M-Conv network model structure | |
在训练模型时,对于特定的代表点,以相同的顺序连续使用相同的一组邻近点显然没有任何好处,因此随机采样并打乱点的输入顺序,代表点的邻近点集和顺序就会因批次而异,如此可以加强模型稳定性。实验发现,经最后一层M-Conv处理所得到的特征依旧是无序的,因此连接完全连接层之前,将最后一层的特征进行变换,可以得到更好的结果。算法1的第1行实现了
1)在代表点K邻域内组成K
2)对矩阵
3)计算协方差矩阵C=
4)计算协方差矩阵C的特征根。
使用
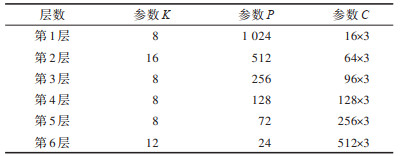
经过实验研究,得到M-Conv模型最优参数如表 1所示,其中K、P、C分别表示邻域大小、代表点数量及输出特征通道数量。本文采用表 1所示的M-Conv最优参数模型结构,在公开的数据集ModelNet40上进行分类实验,并与其他方法所得结果进行比较。ModelNet40数据集是一个包含40个类别三维点云模型数据集,共9 840个训练模型,2 468个测试模型。实验平台为搭载GeForce RTX 3090 GPU的服务器,配置环境为Python3.8及Tensorflow2.4-GPU。
|
下载CSV 表 1 M-Conv最优参数模型结构 Table 1 M-Conv optimal parameter model structure |
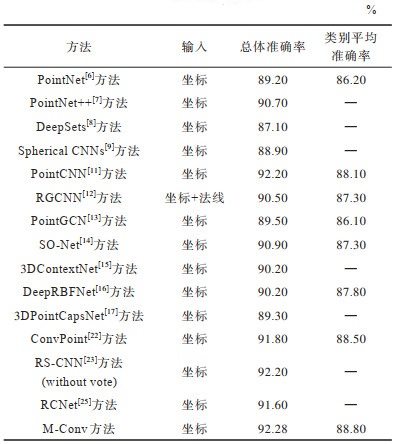
使用ModelNet40数据集及M-Conv最优参数模型结构进行实验,使用总体准确率和类别平均准确率两大指标进行表征,结果如表 2所示,本文方法在这2个指标上均有一定提高。总体准确率虽只略高于PointCNN及RS-CNN,但与其他方法相比有较大提升。在类别平均准确率的比较上,本文方法有明显提升,可见该方法在每个类别的识别上均具有较强的能力,针对不同类别物体所提取的特征更准确,能更好地区分与识别不同物体所带有的不同特征信息。
|
下载CSV 表 2 ModelNet40数据集实验结果对比 Table 2 Comparison of experimental results of ModelNet40 dataset |
与其他现有的方法相比,本文方法具有其独特的优势。现有方法在变换矩阵的获取上一般采用监督学习的方式,例如PointCNN、RS-CNN等,其采用学习的方式得到变换矩阵,因此产生额外的参数,并占用大量资源如CPU、GPU等。本文方法不需要通过学习获得变换矩阵,而是直接根据所构建的亲疏度矩阵计算得到所需要的变换矩阵,这种方式不会产生额外的参数,因此在同等情况下,本文方法的参数更少,占用资源更少,训练更快捷迅速且达到相同准确率所需的迭代次数更少。设置数据集批次大小128,在GeForceRTX 3090 GPU上进行实验时,本文的方法训练一个批次只需0.33 s,明显快于PointCNN训练一个批次所需的0.43 s。
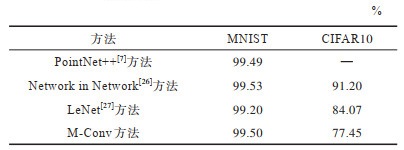
3.2 MNIST和CIFAR10数据集实验为进一步证明M-Conv方法的有效性及稳定性,本文在MNIST和CIFAR10数据集上进行实验验证,实验结果如表 3所示。在总体准确率的比较上,本文方法展现出了与其他方法相当的能力,可见该方法不仅适用于点云的识别与分类,而且适用于图像处理。
|
下载CSV 表 3 MNIST和CIFAR10数据集实验结果比较 Table 3 Comparison of experimental results between MNIST and CIFAR10 datasets |
本文旨在保持网络结构深度的同时,使更深的代表点能表达整个形状的更大部分。为探究各参数对实验结果造成的影响,本文在ModelNet40数据集上进行了一系列对比实验。
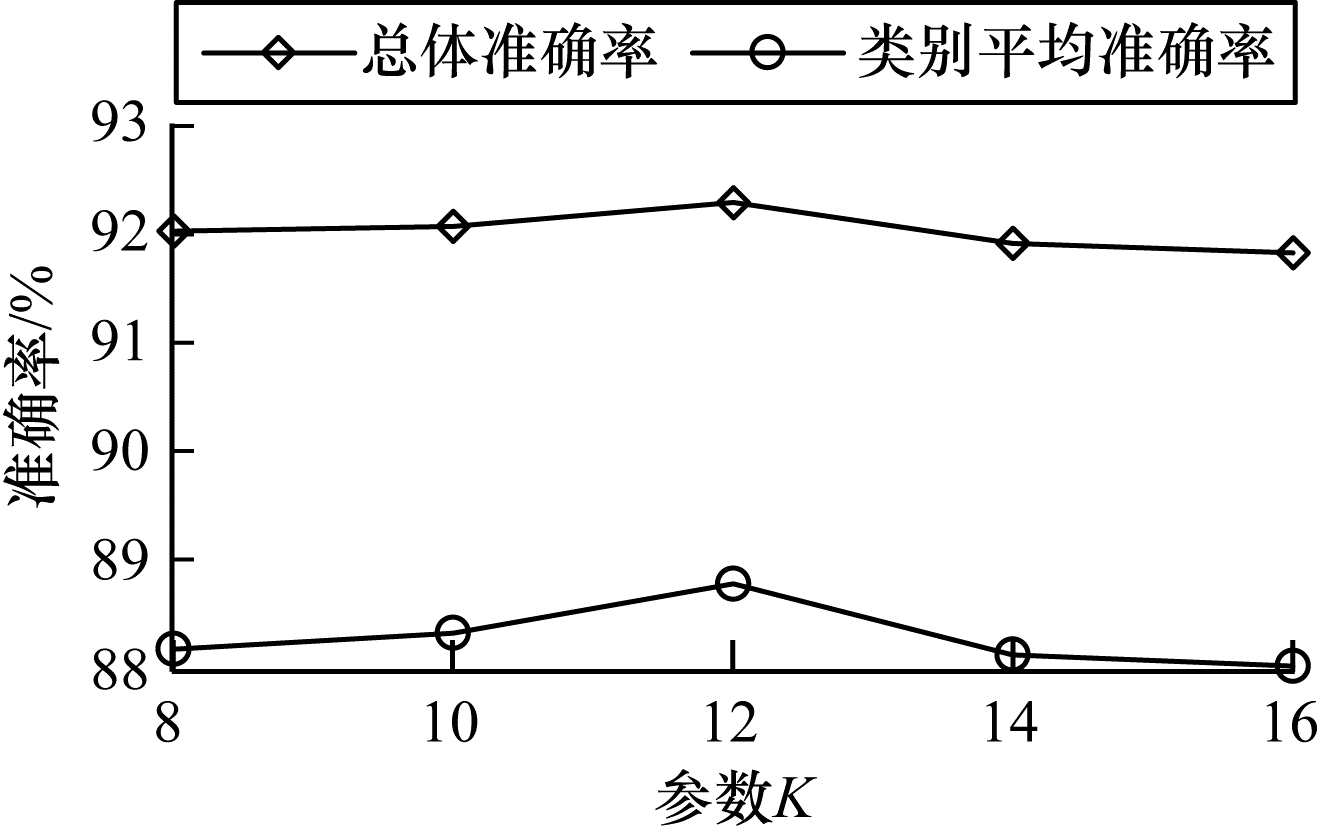
保持M-Conv模型前5层最优参数值及第6层P、C值不变,设置第6层的K值分别为8、10、12、14、16进行对比实验,结果如图 4所示。研究发现,当第6层K值为12时会取得最好的实验结果。当K值选取小于12的值时,总体准确率和类别平均准确率均呈现上升趋势,当K值选取大于12的值时,总体准确率和类别平均准确率均呈现下降趋势。因此最终选取12作为本层K值,前5层K值亦通过此方法得出,第1层~第5层的K值分别为8、16、8、8、8。
|
Download:
|
| 图 4 M-Conv模型第6层参数K值对实验结果的影响 Fig. 4 Influence of the K value of the sixth layer of M-Conv model on experimental results | |
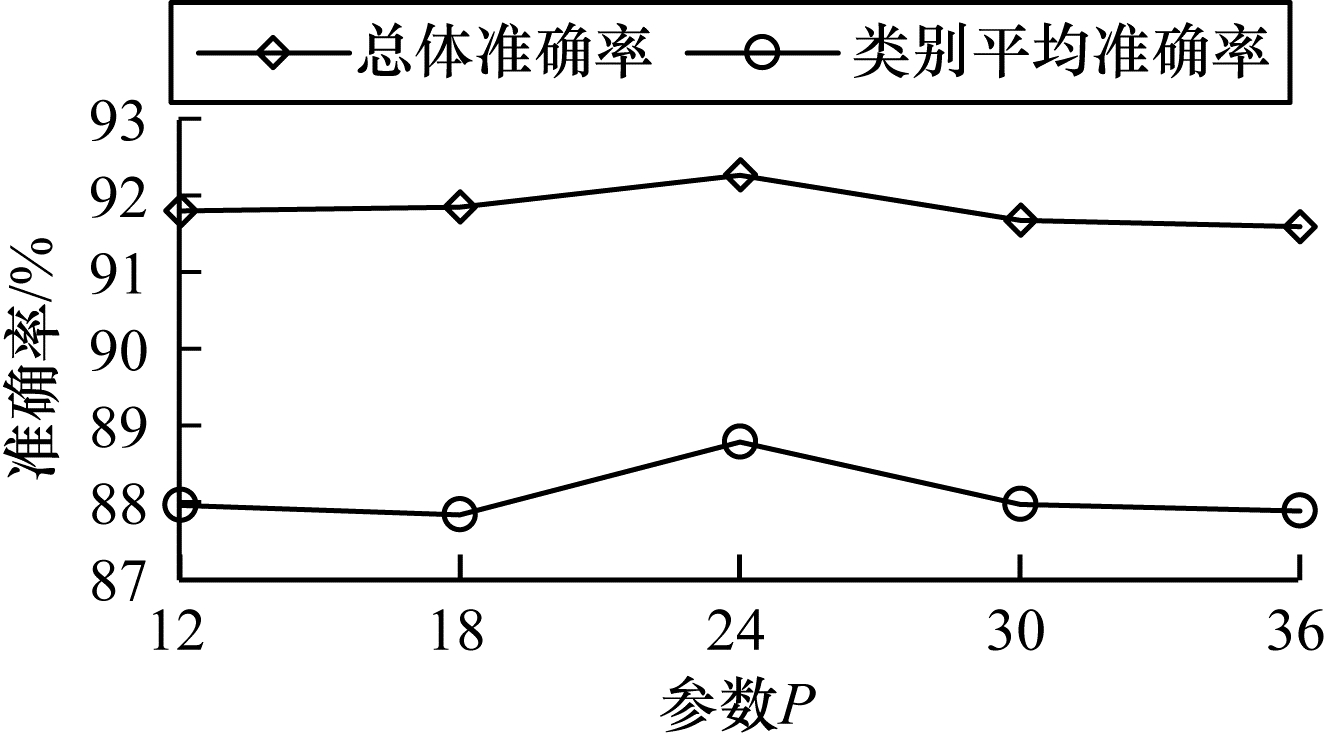
保持M-Conv模型前5层最优参数值及第6层K、C值不变,设置第6层P值分别为12、18、24、30、36进行对比实验,结果如图 5所示。研究发现,当第6层P值为24时会取得最好的实验结果。当P值选取小于24的值时,总体准确率呈现上升趋势,类别平均准确率在P值为12~18时呈下降趋势,在P值为18~24处呈上升趋势,但总体呈现上升趋势。当P值选取小于24的值时,总体准确率和类别平均准确率均呈现下降趋势。最终选取24作为本层P值,前5层的P值亦通过此方法得出,第1层~第5层的P值分别为1 024、512、256、128、72。
|
Download:
|
| 图 5 M-Conv模型第6层参数P值对实验结果的影响 Fig. 5 Influence of the P value of the sixth layer of M-Conv model on experimental results | |
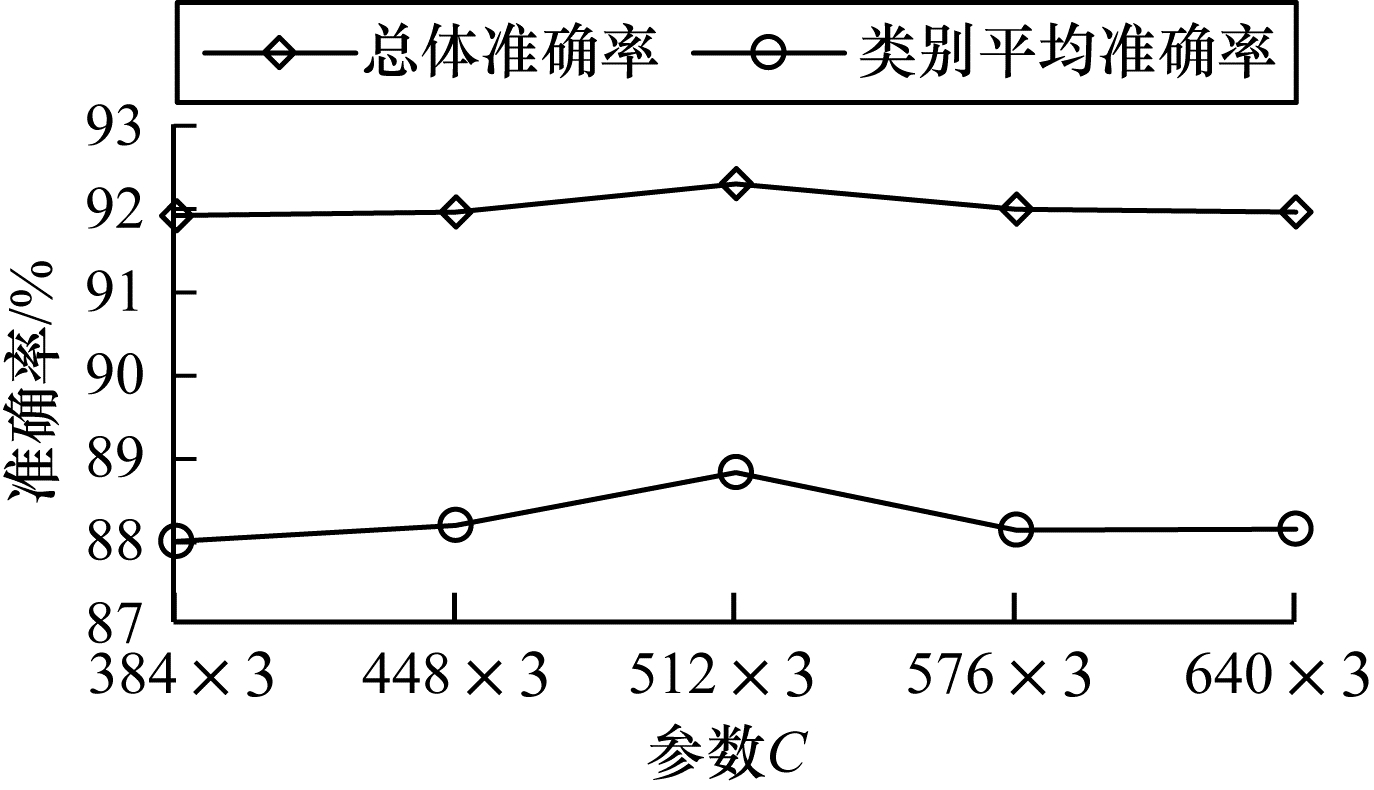
保持M-Conv模型前5层最优参数值及第6层K、P值不变,设置第6层的C值分别为384
|
Download:
|
| 图 6 M-Conv模型第6层参数C值对实验结果的影响 Fig. 6 Influence of the C value of the sixth layer of M-Conv model on experimental results | |
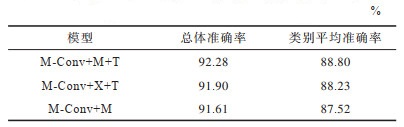
为解决点云空间旋转不变的问题,本文方法在第1层输入时将点坐标映射到曲率特征空间,这会比单纯地将X、Y、Z坐标作为输入更有效。最后一层M-Conv处理所得到的特征依旧是无序的,现有的方法不会在连接完全连接层之前将卷积得到的特征进行变换,而本文方法在连接完全连接层之前会对最后一层的特征再做一次变换,使之由无序状态转变为有序状态。表 4所示为模型调整实验结果,表 4中的M代表输入时将点坐标映射到曲率特征空间,X代表输入时使用点云三维坐标,T代表对最后一层M-Conv处理后得到的特征进行变换。在使用本文核心方法M-Conv的基础上,在输入时将点坐标映射到曲率特征空间,并对最后一层M-Conv处理得到的特征进行变换,以取得更好的效果。若直接将点云X、Y、Z坐标作为输入,总体准确率和类别平均准确率均有小幅下降。若输入时将点坐标映射到曲率特征空间,但不对最后一层M-Conv处理得到的特征进行变换,总体准确率和类别平均准确率均有较大幅度的下降,类别平均准确率更是下降1个百分点以上,可见对最后一层的特征进行变换可以使准确率得到有效提升。
|
下载CSV 表 4 模型调整实验结果 Table 4 Experimental results of model adjustment |
零部件分割是点云形状分析中一项具有挑战性的任务,为验证M-Conv模型针对分割任务的有效性及可行性,本文在ShapeNet数据集上进行了分割实验。ShapeNet数据集是点云零部件分割数据集,包含16个类别和50个分割实例,每个对象有2~6个零部件标签,例如飞机的机翼。在16 881个点云模型中,将14 007个模型用于训练,另外2 874个模型用于测试。
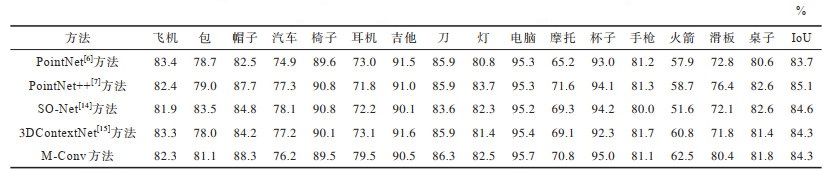
使用ShapeNet数据集进行零部件分割实验,结果如表 5所示,其中IoU代表总体交并比。由表 5可知,M-Conv模型的实验结果与其他方法的水平相当,甚至在某些类别上实现了超越。表 5列举了每个类别的交并比,M-Conv模型在帽子、耳机、刀、电脑、杯子、火箭及滑板7个类别上均取得了最佳结果。图 7展示了上述7个类别的分割效果,其中第1行为M-Conv模型分割预测结果的可视化图,第2行为真实结果可视化图
|
下载CSV 表 5 ShapeNet数据集实验结果对比 Table 5 Comparison of experimental results of ShapeNet dataset |
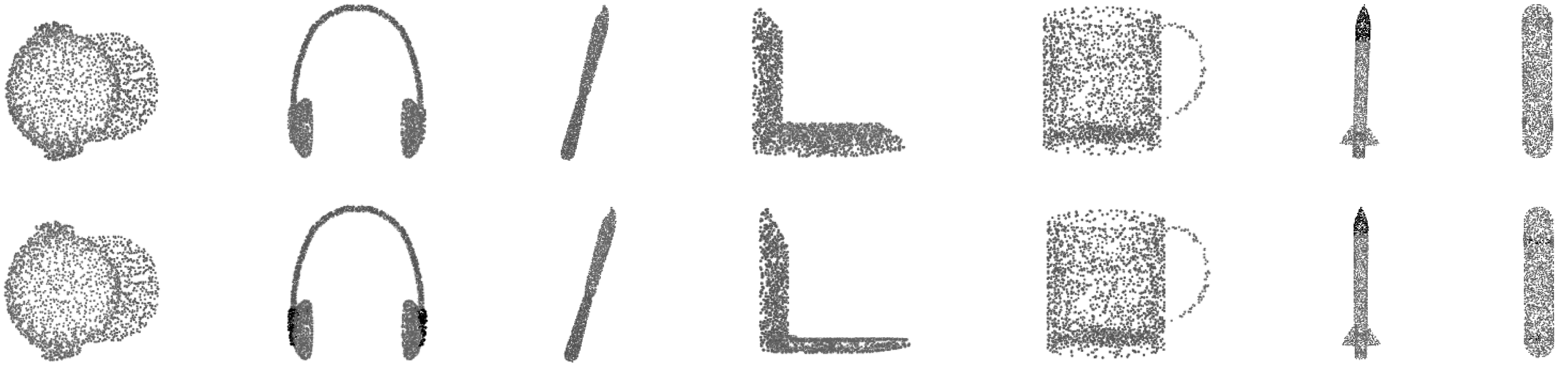
|
Download:
|
| 图 7 ShapeNet数据集分割实例 Fig. 7 ShapeNet dataset segmentation example | |
表 6总结了M-Conv模型的时间复杂度和空间复杂度。M-Conv模型的参数数量略多于其他方法,但浮点运算数指标远胜于其他方法,展示了其巨大的优势及潜力。
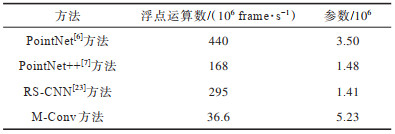
|
下载CSV 表 6 不同方法的复杂度对比 Table 6 Complexity comparison of different methods |
本文提出一种基于卷积神经网络的模型,利用点云数据的空间局部相关性,将点云坐标映射到曲率特征空间以提取旋转不变的特征。使用K邻域内的点集合构建基于欧式内积的亲疏度矩阵,对亲疏度矩阵特征值进行排序后,将对应的特征向量组成变换矩阵,从而对特征进行变换,以实现置换不变性。实验结果表明,该方法在分类任务和分割任务上均取得了较好的结果。但该方法在邻域点的选择上采用了KNN算法,并不能很好地计算三维物体表面点与点之间的真实距离。下一步考虑把一些在几何处理上表现良好的方法如Deep Points[28]、Deep Geodesic Networks[29]等与本文方法相结合,并在邻域点的选择上进行优化,从而得到更好的分类及分割效果。
| [1] |
SU H, MAJI S, KALOGERAKIS E, et al. Multi-view convolutional neural networks for 3D shape recognition[C]//Proceedings of IEEE International Conference on Computer Vision. Washington D.C., USA: IEEE Press, 2015: 945-953.
|
| [2] |
YANG Z, WANG L W. Learning relationships for multi-view 3D object recognition[C]//Proceedings of IEEE/CVF International Conference on Computer Vision. Washington D.C., USA: IEEE Press, 2019: 7504-7513.
|
| [3] |
顾砾, 季怡, 刘纯平. 基于多模态特征融合的三维点云分类方法[J]. 计算机工程, 2021, 47(2): 279-284. GU L, JI Y, LIU C P. Classification method of three-dimensional point cloud based on multiple modal feature fusion[J]. Computer Engineering, 2021, 47(2): 279-284. (in Chinese) |
| [4] |
MATURANA D, SCHERER S. VoxNet: a 3D convolutional neural network for real-time object recognition[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington D.C., USA: IEEE Press, 2015: 922-928.
|
| [5] |
WU Z R, SONG S R, KHOSLA A, et al. 3D ShapeNets: a deep representation for volumetric shapes[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2015: 1912-1920.
|
| [6] |
CHARLES R Q, HAO S, MO K C, et al. PointNet: deep learning on point sets for 3D classification and segmentation[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2017: 77-85.
|
| [7] |
QI C R, YI L, SU H, et al. PointNet++: deep hierarchical feature learning on point sets in a metric space[EB/OL]. [2021-08-16]. https://arxiv.org/abs/1706.02413.
|
| [8] |
ZAHEER M, KOTTUR S, RAVANBAKHSH S, et al. Deep sets[EB/OL]. [2021-08-16]. https://arxiv.org/abs/1703.06114.
|
| [9] |
ESTEVES C, ALLEN-BLANCHETTE C, MAKADIA A, et al. Learning SO(3) equivariant representations with spherical CNNs[J]. International Journal of Computer Vision, 2020, 128(3): 588-600. DOI:10.1007/s11263-019-01220-1 |
| [10] |
COHEN T S, GEIGER M, KOEHLER J, et al. Spherical CNNs[EB/OL]. [2021-08-16]. https://arxiv.org/abs/1801.10130.
|
| [11] |
LI Y, BU R, SUN M, et al. PointcCNN: convolution on X-transformed points[EB/OL]. [2021-08-16]. https://arxiv.org/abs/1801.07791.
|
| [12] |
TE G S, HU W, ZHENG A M, et al. RGCNN: regularized graph CNN for point cloud segmentation[C]//Proceedings of the 26th International Conference on Multimedia. New York, USA: ACM Press, 2018: 746-754.
|
| [13] |
ZHANG Y X, RABBAT M. A graph-CNN for 3D point cloud classification[C]//Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing. Washington D.C., USA: IEEE Press, 2018: 6279-6283.
|
| [14] |
LI J X, CHEN B M, LEE G H. SO-net: self-organizing network for point cloud analysis[C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2018: 9397-9406.
|
| [15] |
ZENG W, GEVERS T. 3D ContextNet: k-d tree guided hierarchical learning of point clouds using local and global contextual cues[C]//Proceedings of Conference on Computer Vision. Berlin, Germany: Springer, 2019: 314-330.
|
| [16] |
CHEN W K, HAN X G, LI G B, et al. Deep RBFNet: point cloud feature learning using radial basis functions[EB/OL]. [2021-08-16]. Berlin, Germany: Springer, https://arxiv.org/abs/1812.04302.
|
| [17] |
ZHAO Y H, BIRDAL T, DENG H W, et al. 3D point capsule networks[C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2019: 1009-1018.
|
| [18] |
田钰杰, 管有庆, 龚锐. 一种鲁棒的多特征点云分类分割深度神经网络[J]. 计算机工程, 2021, 47(11): 234-240. TIAN Y J, GUAN Y Q, GONG R. A robust deep neural network for multi-feature point cloud classification and segmentation[J]. Computer Engineering, 2021, 47(11): 234-240. (in Chinese) |
| [19] |
SUN X, LIAN Z H, XIAO J G. SRINet: learning strictly rotation-invariant representations for point cloud classification and segmentation[C]//Proceedings of the 27th ACM International Conference on Multimedia. New York, USA: ACM Press, 2019: 980-988.
|
| [20] |
THOMAS N, SMIDT T, KEARNES S, et al. Tensor field networks: Rotationand translation equivariant neural networks for 3D point clouds[EB/OL]. [2021-08-16]. https://arxiv.org/abs/1802.08219.
|
| [21] |
POULENARD A, RAKOTOSAONA M J, PONTY Y, et al. Effective rotation-invariant point CNN with spherical harmonics kernels[C]//Proceedings of International Conference on 3D Vision. Washington D.C., USA: IEEE Press, IEEE Press, 2019: 47-56.
|
| [22] |
BOULCH A. ConvPoint: continuous convolutions for point cloud processing[J]. Computers & Graphics, 2020, 88: 24-34. DOI:10.1016/j.cag.2020.02.005 |
| [23] |
LIU Y C, FAN B, XIANG S M, et al. Relation-shape convolutional neural network for point cloud analysis[C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2019: 8887-8896.
|
| [24] |
WU W X, QI Z A, LI F X. PointConv: deep convolutional networks on 3D point clouds[C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2019: 9613-9622.
|
| [25] |
WU P X, CHEN C, YI J R, et al. Point cloud processing via recurrent set encoding[C]//Proceedings of AAAI Conference on Artificial Intelligence. New York, USA: AAAI Press, 2019: 5441-5449.
|
| [26] |
LIN M, CHEN Q, YAN S. Network in network[EB/OL]. [2021-08-16]. https://arxiv.org/abs/1312.4400.
|
| [27] |
LECUN Y, BOTTOU L, BENGIO Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324. DOI:10.1109/5.726791 |
| [28] |
WU S H, HUANG H, GONG M L, et al. Deep points consolidation[J]. ACM Transactions on Graphics, 2015, 34(6): 1-13. |
| [29] |
HE T, HUANG H B, YI L, et al. GeoNet: deep geodesic networks for point cloud analysis[C]//Proceedings of 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2019: 6888-6897.
|
 2022, Vol. 48
2022, Vol. 48

