开放科学(资源服务)标志码(OSID):
同步定位与建图(Simultaneous Localization and Mapping,SLAM)技术在移动机器人状态估计及环境感知领域起到重要作用。根据传感器的不同,SLAM技术分为视觉SLAM以及激光SLAM技术[1-2]。基于视觉SLAM技术的方法适用于位置识别,但容易受到低纹理、光照、剧烈运动的影响;而基于激光SLAM技术的方法能够捕捉远程环境的细节信息,精度较高,但会受退化场景的影响。多传感器融合的SLAM技术将相机、激光雷达、惯性传感器(Inertial Measurement Unit,IMU)相结合,能够进一步提高SLAM系统的鲁棒性和精度。因此,激光雷达、相机及IMU融合的SLAM系统也越来越受到人们的关注。
目前多传感器融合的SLAM系统主要分为视觉惯性系统(Visual Inertial System,VIS)、雷达惯性系统(Lidar Inertial System,LIS)及激光雷达视觉惯性系统(Lidar Visual Inertial System,LVIS)。根据传感器的直接或间接融合测量方法,相机与IMU的融合方式主要分为松耦合和紧耦合。松耦合方法[3-4]通过两种方式处理图像和IMU的测量数据,并分别估计相机和IMU的状态,融合得到最终结果。紧耦合方法[5-6]将相机与IMU紧耦合,联合优化估计状态,从而获得高精度的位姿。与松耦合方法相比,紧耦合方法的鲁棒性和精度更高。虽然采用紧耦合融合方式的系统能够实现高精度的位置估计,但依然会受到低纹理场景的影响。因此,研究人员提出PL-SLAM系统[7]、基于单目的点线特征系统[8-10]以及基于双目的点线特征系统[11-12],其中PL-SLAM系统建立在ORB-SLAM系统[13-14]的基础上。HE等[15]提出PL-VIO系统,FU等[16]提出PL-VINS系统,通过在前端引入线特征,对点线特征联合优化,克服了低纹理环境下无法进行特征跟踪的问题。
同样,LIS系统也分为紧耦合和松耦合系统。ZHAO等[17]提出一种实时的激光雷达惯性里程计及建图系统LIOM,该系统通过卡尔曼滤波融合激光雷达和IMU数据,实现准确的位姿估计。文献[18]介绍了一种紧耦合系统,该系统将激光雷达里程计、IMU预积分因子、GPS因子以及回环检测因子引入因子图中,联合优化实现高精度、实时的移动机器人轨迹估计和地图构建。相比于LIOM系统,该系统通过ISAM2实现局部和全局的优化,其鲁棒性和精度更高,但仍然会受到退化场景的影响。
针对退化场景的问题,文献[19]对紧耦合系统进行改进,将激光雷达、相机以及IMU紧耦合,实现了LVIS系统,该系统包含VIS系统和LIS系统,VIS系统采用VINS-MONO系统的方法 [20],而LIS系统依据LIO-SAM系统的方法 [18],将2个子系统紧耦合,完成系统初始化、状态估计和回环检测,当遇到低纹理或退化场景时会进行故障检测,每次故障检测均会重新进行初始化,这样虽然能够阻止系统跟踪失败,但会对定位精度产生影响。
本文结合点线特征的方法对LVI-SAM系统进行改进,在VIS系统前端提取与匹配点线特征,并在后端联合进行BA优化[16],实现点线融合。通过短线剔除策略筛选长线特征,落实稳定有效的线特征跟踪。在LIS系统中,将线特征的端点与激光雷达深度进行关联,完成线特征的深度融合,从而获得准确的空间线特征,进一步提高系统的定位精度。
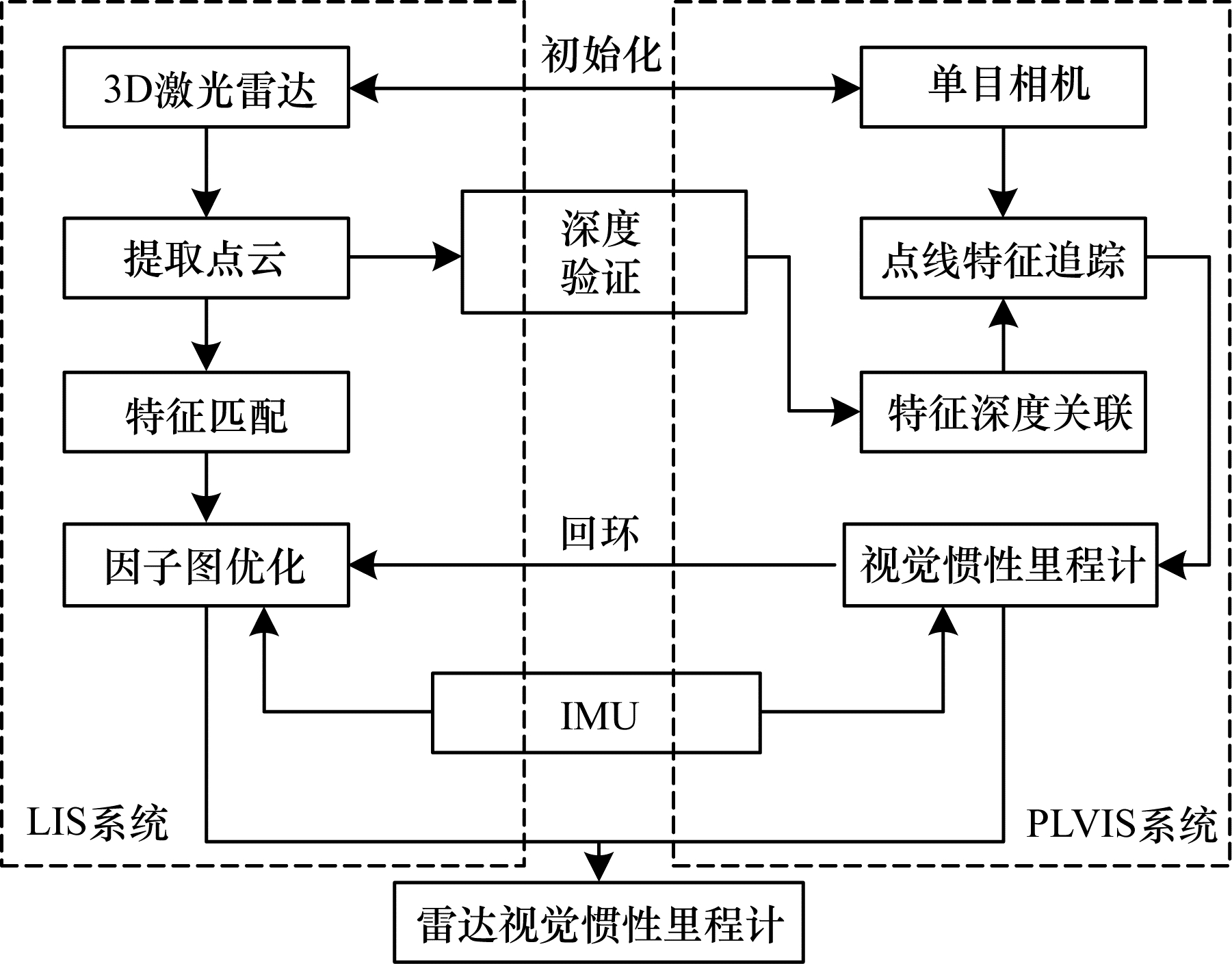
1 本文系统框架本文在LVI-SAM系统的基础上实现PL2VI-SLAM系统,系统的整体框架如图 1所示,该系统融合了视觉惯导紧耦合系统(Point-Line with Visual Inertial System,PLVIS)和LIS系统,PLVIS系统包括相机IMU初始化、特征提取与匹配、位姿跟踪、局部地图构建及回环检测。LIS系统包括雷达、IMU初始化、点云提取与匹配、局部建图及回环检测。相比于LVI-SAM系统,本文系统在PLVIS系统初始化阶段以及前端里程计部分融合了点线特征的提取与匹配,后端采用滑动窗口优化算法限制匹配的点特征与线特征的数量。
|
Download:
|
| 图 1 PL2VI-SLAM系统框架 Fig. 1 Framework of PL2VI-SLAM system | |
相较于VINS-MONO系统,本文系统在初始化阶段增加了线特征,促进系统的初始化进程。通过重投影误差对点线特征进行优化,从而获得三维点线特征,同时以LIS系统的初始化成功与否作为整体系统初始化是否成功的判断依据。初始化成功后根据构建的静态局部地图实现连续帧的位姿估计。
在PLVIS系统跟踪的过程中,同时进行点线特征与关键帧的选择,如果点线特征跟踪的关键帧数量超过设定的阈值
| $ \mathrm{m}\mathrm{i}\mathrm{n}\left[\boldsymbol{p}, \boldsymbol{l}\right]=a $ | (1) |
其中:p是观测到的点特征;
关键帧的数量则使用一个滑动窗口来维护,通过以上方式能够实现PLVIS系统的局部跟踪过程。
最后使用DBOW2词袋模型 [21]实现PLVIS系统回环检测,并联合LIS系统实现整个PL2VI-SLAM系统的回环检测。
2 PL2VI-SLAM系统PL2VI-SLAM系统由PLVIS视觉惯性系统以及LIS雷达惯性系统组成。其中:PLVIS系统包括点线特征的提取与匹配、IMU预积分、点线特征深度关联以及回环检测;LIS系统包括点云特征的提取与匹配、IMU预积分以及回环检测。
2.1 视觉点线特征提取与匹配首先,每一帧图像采用KLT稀疏光流法[22]跟踪前一帧点特征,并提取当前帧新的点特征,使每帧图像中的点特征数量不少于100个,然后在2个相邻特征之间设置最小像素分离值来实现统一的特征分布。根据RANSAC算法的基本矩阵模型[23],能够检验特征的离群值,并剔除离群值大的特征点。通过离群值检验的点将投影到单位球体上,然后延伸到深度归一化平面上,获得特征点的最终位置。
由于OpenCV库中的LSD算法包含大量的短线特征,计算代价较大,若单纯使用LSD算法,很难满足实时性要求。因此采用线特征长度筛选策略,保留主线特征而剔除不必要的短线特征,既能满足实时性要求,又能提高位姿精度。
长度拒绝策略是通过定义特征线的最小长度来拒绝短线特征,线特征长度的最低阈值表达式如式(2)所示:
| $ {L}_{\mathrm{m}\mathrm{i}\mathrm{n}}=\left[u\times \mathrm{m}\mathrm{i}\mathrm{n}\left({W}_{I}, {H}_{I}\right)\right] $ | (2) |
其中:
1) 通过KNN算法计算线特征之间的汉明距离,如果大于30,则剔除,否则保留。
2) 测试所匹配的线特征间的角度是否小于0.1 rad,如果是,则保留,否则剔除。
经过以上2种方法对线特征进行处理后,发现其速度至少是LSD算法的3倍。
2.2 点线特征残差匹配完点线特征后,需要构建点线特征的残差模型。本文依据VINS-MONO系统的方法构建点的残差。定义一个单位球体上的相机测量残差,对于第i帧首次观察到的第
| $ {\boldsymbol{r}}_{c}\left({\boldsymbol{z}}_{n}^{c{}_{j}}, \boldsymbol{X}\right)={\left[{\boldsymbol{b}}_{1}{\boldsymbol{b}}_{2}\right]}^{\mathrm{T}}\times \left({\tilde{\boldsymbol{P}}}_{n}^{{c}_{j}}-\frac{{\boldsymbol{P}}_{n}^{{c}_{j}}}{‖{\boldsymbol{P}}_{n}^{{c}_{j}}‖}\right) $ |
| $ {\tilde{\boldsymbol{P}}}_{n}^{{c}_{j}}={\mathrm{\pi }}_{c}^{-1}\left(\left[\begin{array}{c}{\hat{u}}_{n}^{{c}_{j}}\\ {\hat{v}}_{n}^{{c}_{j}}\end{array}\right]\right) $ |
| $ \begin{array}{l}{\boldsymbol{P}}_{n}^{{c}_{j}}=\\ {\boldsymbol{R}}_{b}^{c}\left({\boldsymbol{R}}_{w}^{{b}_{j}}\left({\boldsymbol{R}}_{{b}_{i}}^{w}\left({\boldsymbol{R}}_{c}^{b}\frac{1}{{\lambda }_{n}}{\mathrm{\pi }}_{c}^{-1}\left(\left[\begin{array}{c}{u}_{n}^{{c}_{j}}\\ {v}_{n}^{{c}_{j}}\end{array}\right]\right)+{\boldsymbol{p}}_{c}^{b}\right)+{\boldsymbol{p}}_{{b}_{i}}^{w}-{\boldsymbol{p}}_{{b}_{j}}^{w}\right)-{\boldsymbol{p}}_{c}^{b}\right)\end{array} $ | (3) |
其中:X是不同时刻下IMU的状态,具体参见公式(7)。
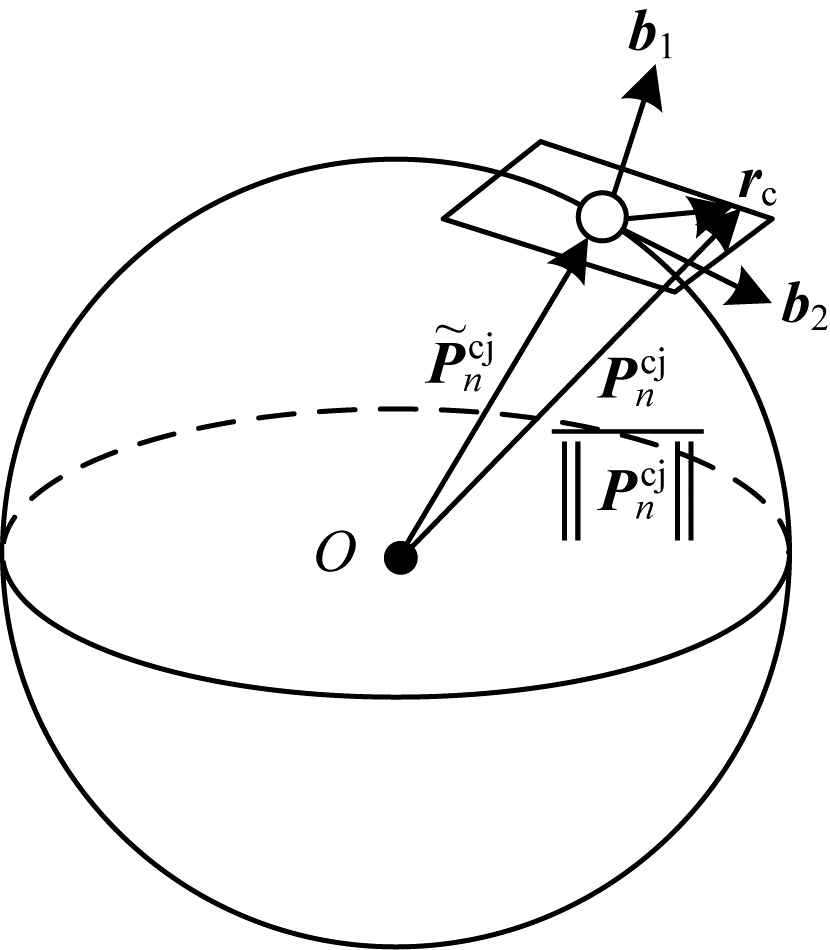
由于视觉残差的自由度为2,因此,将残差向量投影到切平面上,如图 2所示。其中,
|
Download:
|
| 图 2 点特征残差示意图 Fig. 2 Schematic diagram of point feature residuals | |
首先建立图像平面上的线特征对应关系,然后通过三角化这些对应关系来初始化世界坐标系中的空间线
|
Download:
|
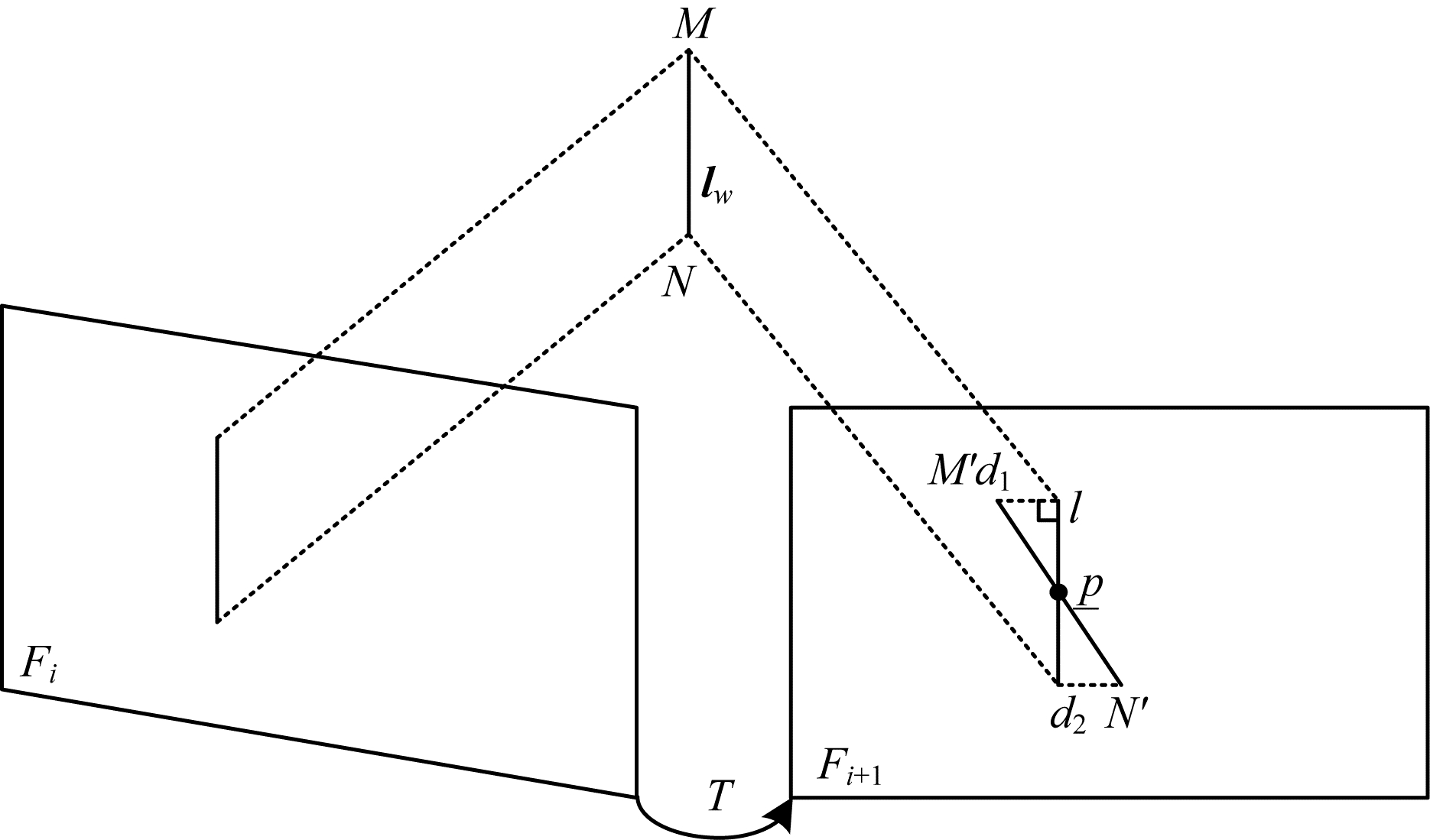
| 图 3 线特征的重投影误差示意图 Fig. 3 Schematic diagram of reprojection error of line features | |
线特征的重投影误差是根据点线距离进行建模的。首先定义空间线,然后定义线的几何变换,给定一个世界坐标系到相机坐标系的变换矩阵
| $ \begin{array}{c}{\boldsymbol{l}}_{c}=\left[\begin{array}{c}{\boldsymbol{n}}_{c}\\ {\boldsymbol{d}}_{c}\end{array}\right]={\boldsymbol{Q}}_{cw}\times {\boldsymbol{l}}_{w}=\left[\begin{array}{cc}{\boldsymbol{R}}_{cw}& {\left[{\boldsymbol{t}}_{cw}\right]}_{\times }{\boldsymbol{R}}_{cw}\\ 0& {\boldsymbol{R}}_{cw}\end{array}\right]\left[\begin{array}{c}{\boldsymbol{n}}_{w}\\ {\boldsymbol{d}}_{w}\end{array}\right]\end{array} $ | (4) |
将
| $ l={\left[{l}_{1}, {l}_{2}, {l}_{3}\right]}^{\mathrm{T}}={\boldsymbol{K}}_{l}{\boldsymbol{n}}_{c} $ | (5) |
其中:
| $ {\boldsymbol{r}}_{l}\left({\boldsymbol{z}}_{{\boldsymbol{l}}_{j}}^{{\boldsymbol{c}}_{i}}, \boldsymbol{X}\right)=d\left(p, l\right)=\frac{\underset{—}{{p}^{\rm{T}}}\times l}{\sqrt[]{{l}_{1}^{2}+{l}_{2}^{2}}} $ | (6) |
其中:
无论是子系统的初始化还是状态估计,都离不开IMU积分模型。通过IMU积分可以获得机器人在任意时刻的位置、速度以及姿态,从而为本文系统提供高精度的状态估计。而在IMU积分的过程中,系统会受到加速度和陀螺仪偏置的影响,如果每次计算都要将IMU坐标系转换到世界坐标系,计算量将非常大,严重影响系统的实时性,因此本文采用IMU预积分模型[27]。
对于PLVIS子系统,当初始化完成后,将激光雷达测量的特征深度值关联到视觉里程计中,从而获得一个用于特征深度估计的关键帧。将关键帧对应的不同时刻的状态定义为:
| $ \boldsymbol{X}=\left[\boldsymbol{R}, \boldsymbol{p}, \boldsymbol{v}, \boldsymbol{b}\right] $ | (7) |
其中:
1) 初始化。对于PLVIS系统,初始化的质量在很大程度上取决于IMU传感器的运动和精度,当IMU传感器以较小速度或匀速移动时,VINS-MONO系统无法进行初始化,这是因为当加速度不大时,尺度无法观测,而IMU传感器的偏置和噪声影响了原始加速度的测量,所以初始化能够对这些参数有良好的猜测,会使后续的迭代优化更快收敛。相比于VINS-MONO系统,本文系统在初始化时,首先初始化LIS系统,并获得状态
2) IMU预积分。根据IMU传感器的原始信息,可以定义IMU传感器的测量值为:
| $ {\hat{\boldsymbol{w}}}_{t}={\boldsymbol{w}}_{t}+{\boldsymbol{b}}_{t}^{w}+{\boldsymbol{n}}_{t}^{w} $ | (8) |
| $ {\hat{\boldsymbol{a}}}_{t}={\boldsymbol{R}}_{t}^{\mathrm{B}\mathrm{W}}\left({\boldsymbol{a}}_{t}-\boldsymbol{g}\right)+{\boldsymbol{b}}_{t}^{\boldsymbol{a}}+{\boldsymbol{n}}_{t}^{\boldsymbol{a}} $ | (9) |
其中:
根据IMU测量值,可以得到相机在不同时刻的位置、速度以及旋转状态的表达式如下所示:
| $ {\boldsymbol{v}}_{t+\Delta t}={\boldsymbol{v}}_{t}+\boldsymbol{g}\Delta t+{\boldsymbol{R}}_{t}\left({\hat{\boldsymbol{a}}}_{t}-{\boldsymbol{b}}_{t}^{\boldsymbol{a}}-{\boldsymbol{n}}_{t}^{\boldsymbol{a}}\right)\Delta t $ | (10) |
| $ \begin{array}{l}{\boldsymbol{p}}_{t+\Delta t}={\boldsymbol{p}}_{t}+{\boldsymbol{v}}_{t}\Delta t+\frac{1}{2}\boldsymbol{g}\Delta {t}^{2}+\frac{1}{2}{\boldsymbol{R}}_{t}\left({\hat{\boldsymbol{a}}}_{t}-{\boldsymbol{b}}_{t}^{\boldsymbol{a}}-{\boldsymbol{n}}_{t}^{\boldsymbol{a}}\right)\Delta {t}^{2}\\ \end{array} $ | (11) |
| $ {\boldsymbol{R}}_{t+\Delta t}={\boldsymbol{R}}_{t}\mathrm{e}\mathrm{x}\mathrm{p}\left(\left({\hat{\boldsymbol{w}}}_{t}-{\boldsymbol{b}}_{t}^{w}-{\boldsymbol{n}}_{t}^{w}\right)\Delta t\right) $ | (12) |
其中:
由于
| $ \Delta {\boldsymbol{v}}_{ij}={\boldsymbol{R}}_{i}^{\mathrm{T}}\left({\boldsymbol{v}}_{j}-{\boldsymbol{v}}_{i}-\boldsymbol{g}\Delta {t}_{ij}\right) $ | (13) |
| $ \Delta {\boldsymbol{p}}_{ij}={\boldsymbol{R}}_{i}^{\mathrm{T}}\left({\boldsymbol{p}}_{j}-{\boldsymbol{p}}_{i}-{\boldsymbol{v}}_{i}\Delta {t}_{ij}-\frac{1}{2}\boldsymbol{g}\Delta {t}_{ij}^{2}\right) $ | (14) |
| $ \Delta {\boldsymbol{R}}_{ij}={\boldsymbol{R}}_{i}^{\mathrm{T}}{\boldsymbol{R}}_{j} $ | (15) |
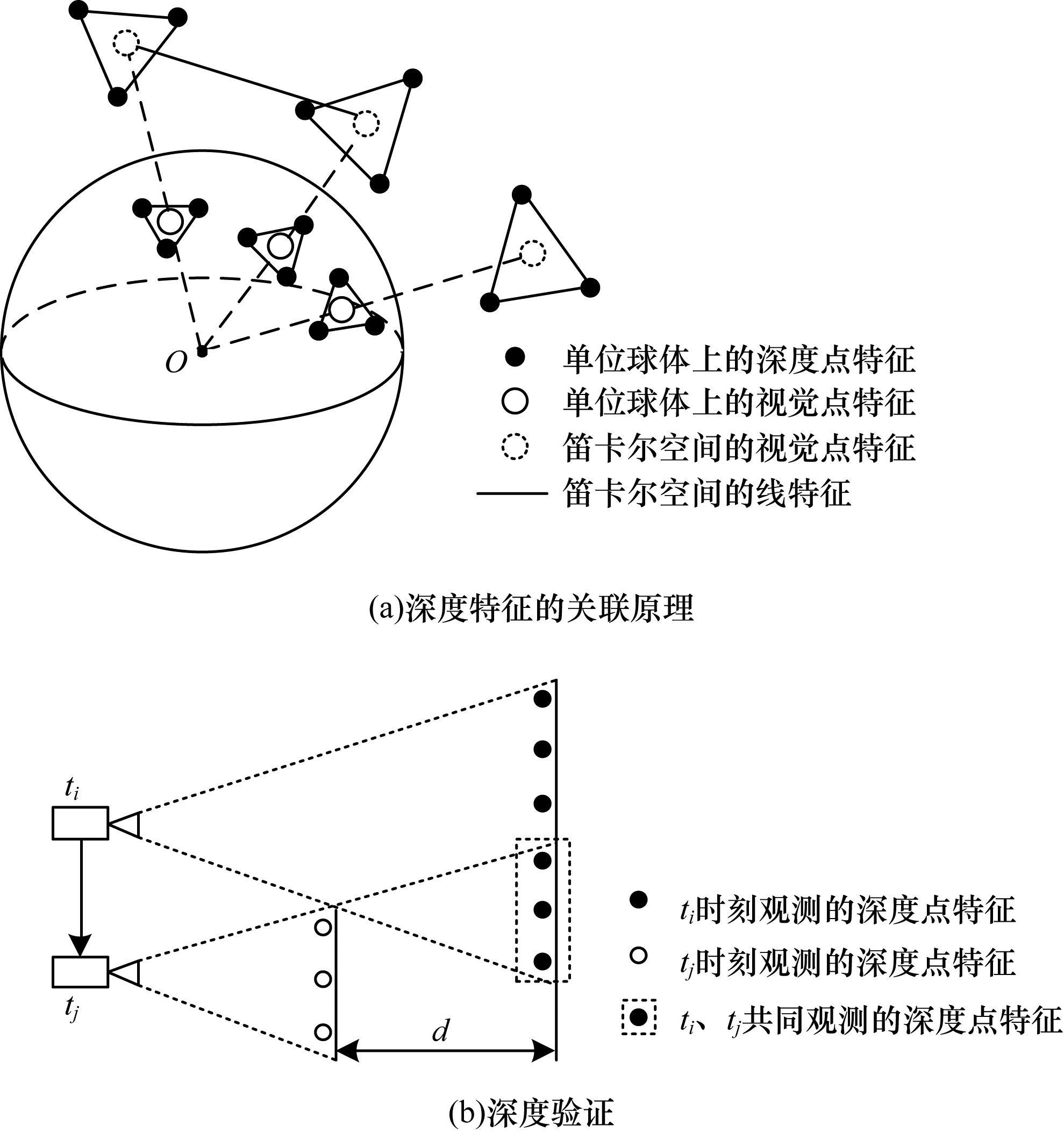
3) 特征深度关联。在PLVIS系统初始化以及视觉里程计中,本文将LIS系统中激光雷达测量的深度值作为视觉特征的深度。由于激光雷达产生的是稀疏的点云,因此需要通过叠加多个激光雷达帧,才能获得特征密集的深度图。相比于LVI-SAM系统,本文系统不仅将点特征与深度值关联起来,而且将线特征端点与深度值联系起来。将点特征、线特征端点、激光雷达深度点投影到一个单位球体上。此时,降采样激光雷达深度点云在单位球体上利用视觉特征的极坐标搜索二维K-D树。找到球体上对应距离最近的3个深度特征,此特征深度即为相机中心到视觉特征的距离。同理,可以获得线特征端点的深度。视觉点线特征的深度关联示意图如图 4所示,其中,虚线的长度代表特征深度。
|
Download:
|
| 图 4 视觉点线特征的深度关联 Fig. 4 Visual point-line feature depth association | |
投影到球体上的3个深度特征进行逆投影后,它们的距离可能相差甚远,如图 4(b)所示,

|
Download:
|
| 图 5 深度特征关联前后的效果图 Fig. 5 Effect drawing before and after depth feature association | |
4) 故障检测。PLVIS系统容易受到剧烈运动、光照变化和低纹理环境影响。当机器人经历剧烈运动或进入低纹理环境时,被跟踪特征的数量将大大减少,可能会导致优化失败,并产生较大的IMU偏差。LVI-SAM系统的解决办法是当跟踪的特征数量低于阈值时,系统进行故障检测并重新进行初始化。但每次初始化时,如果PLVIS系统遇到低纹理场景,初始化将失败,导致定位失败,定位精度降低。因此,本文加入线特征,只有当跟踪的线特征数量低于阈值时才进行故障检测。
5) 视觉回环检测。回环检测模块利用了DBoW2词袋模型,当新的关键帧到来时,将提取简短的二进制BRIEF描述子[28],并且将其与之前的描述子进行匹配,如果相似度超过了设定的阈值,即可判定该帧是一个回环帧。此外,PLVIS系统一旦检测到回环,就会将此信息传达给LIS系统,并将DBoW2词袋模型得到的回环帧的时间戳发送给LIS系统进行验证,如果该时间戳对应的关键帧在LIS系统里也是回环帧,则可验证该帧为回环帧。
2.4 LIS子系统图 1左侧所示为基于LIO-SAM系统实现的LIS子系统框架。LIO-SAM系统中的因子图包含了IMU预积分因子、激光雷达里程计因子、回环检测因子以及可选的GPS因子。而LIS子系统还包含了视觉里程计因子,并将它们添加到因子图中,通过ISAM2算法 [29]优化,获得一个高精度的里程计。IMU预积分过程在2.3节已介绍过,在因子图中,只需添加IMU预积分和视觉里程计估计的状态,并与其他因子进行联合优化。因此,下文仅介绍激光雷达里程计和回环检测。
1) 激光雷达里程计约束。在LIS子系统中,若要实现一个完整的激光雷达里程计,需要对激光雷达检测到的点云特征进行提取与匹配。本文采用LOAM系统的特征提取方式,根据局部区域点的曲率来提取边缘和平面的特征。若将第
| $ {\boldsymbol{F}}_{i}=\left\{{\boldsymbol{F}}_{i}^{e}\text{,}{\boldsymbol{F}}_{i}^{p}\right\} $ | (16) |
由于LIS系统是基于LIO-SAM系统实现的,其关键帧的选择是通过一种简单有效的启发式方法:与之前的状态
| $ {\boldsymbol{M}}_{i}=\left\{{\boldsymbol{M}}_{i}^{e}, {\boldsymbol{M}}_{i}^{p}\right\} $ |
| $ {\boldsymbol{M}}_{i}^{e}={\hat{\boldsymbol{F}}}_{i}^{e}\bigcup {\hat{\boldsymbol{F}}}_{i-1}^{e}\bigcup \cdots \bigcup {\hat{\boldsymbol{F}}}_{i-n}^{e} $ |
| $ {\boldsymbol{M}}_{i}^{p}={\hat{\boldsymbol{F}}}_{i}^{p}\bigcup {\hat{\boldsymbol{F}}}_{i-1}^{p}\bigcup \cdots \bigcup {\hat{\boldsymbol{F}}}_{i-n}^{p} $ | (17) |
其中:
| $ {\boldsymbol{d}}_{{e}_{k}}=\frac{\left|\left({\boldsymbol{p}}_{i+1, k}^{e}-{\boldsymbol{p}}_{i, u}^{e}\right)\times \left({\boldsymbol{p}}_{i+1, k}^{e}-{\boldsymbol{p}}_{i, v}^{e}\right)\right|}{\left|{\boldsymbol{p}}_{i, u}^{e}-{\boldsymbol{p}}_{i, v}^{e}\right|} $ | (18) |
| $ {\boldsymbol{d}}_{{p}_{k}}=\frac{\left|\left({\boldsymbol{p}}_{i, u}^{p}-{\boldsymbol{p}}_{i, w}^{p}\right)\times \left({\boldsymbol{p}}_{i, u}^{p}-{\boldsymbol{p}}_{i, w}^{p}\right)\times \left({\boldsymbol{p}}_{i+1, k}^{p}-{\boldsymbol{p}}_{i, u}^{p}\right)\right|}{\left|\left({\boldsymbol{p}}_{i, u}^{p}-{p}_{i, v}^{p}\right)\times \left({\boldsymbol{p}}_{i, u}^{p}-{\boldsymbol{p}}_{i, w}^{p}\right)\right|} $ | (19) |
尽管激光雷达可以很好地提供深度特征,然而如果遇到退化场景,也会误匹配。不仅会影响LIS系统的状态估计,也会影响PLVIS系统的状态估计。因此,本文利用文献[30]提出的方法,将扫描匹配中的非线性问题表示成迭代求解的线性问题:
| $ \underset{\mathrm{T}}{\mathrm{m}\mathrm{i}\mathrm{n}}{‖\boldsymbol{A}\boldsymbol{Q}-\boldsymbol{b}‖}^{2} $ | (20) |
其中:
2) 回环检测。回环检测是根据点云之间的欧几里得距离实现的,能通过ISAM2算法集成到因子图中。当一个新的状态
首先选用EUROC数据集对线特征匹配效果进行分析,然后使用LVI-SAM系统提供的手持式handled数据集以及移动小车jackal数据集进行定位精度分析。最后,为验证本文系统的有效性,将realsensD435i相机、xsens惯导传感器以及VLP16线激光雷达刚性连接在一起,并标定它们之间的外参,手持传感器录制一个长走廊的数据集,并对端到端的误差进行评估。本文选用的数据集包含低纹理和退化场景。实验设备配置为4核i7处理器,8 GB内存,GTX1060,ubuntu16.04操作系统。
3.1 线特征匹配效果基于EUROC的V1_03数据集,选取相邻2个关键帧对线特征进行匹配,匹配结果如图 6所示(彩色效果见《计算机工程》官网HTML版本)。

|
Download:
|
| 图 6 不同算法的匹配结果对比 Fig. 6 Comparison of matching results of different algorithms | |
从图 6可以看出,当场景中的纹理较少时,LSD算法虽然能够进行线特征匹配,但会存在大量的短线特征与误匹配,如图中的黄线所示。而本文算法能剔除短线特征,在提高计算速度的同时也减少了误匹配,效果明显比LSD算法好。对线特征匹配数量及耗时进行对比分析,结果如表 1所示。

|
下载CSV 表 1 匹配耗时及匹配数量对比 Table 1 Comparison of matching time and matching quantity |
由表 1可知,LSD算法匹配耗时最长,而本文算法保留了主线特征,且匹配速度是LSD算法的3倍。
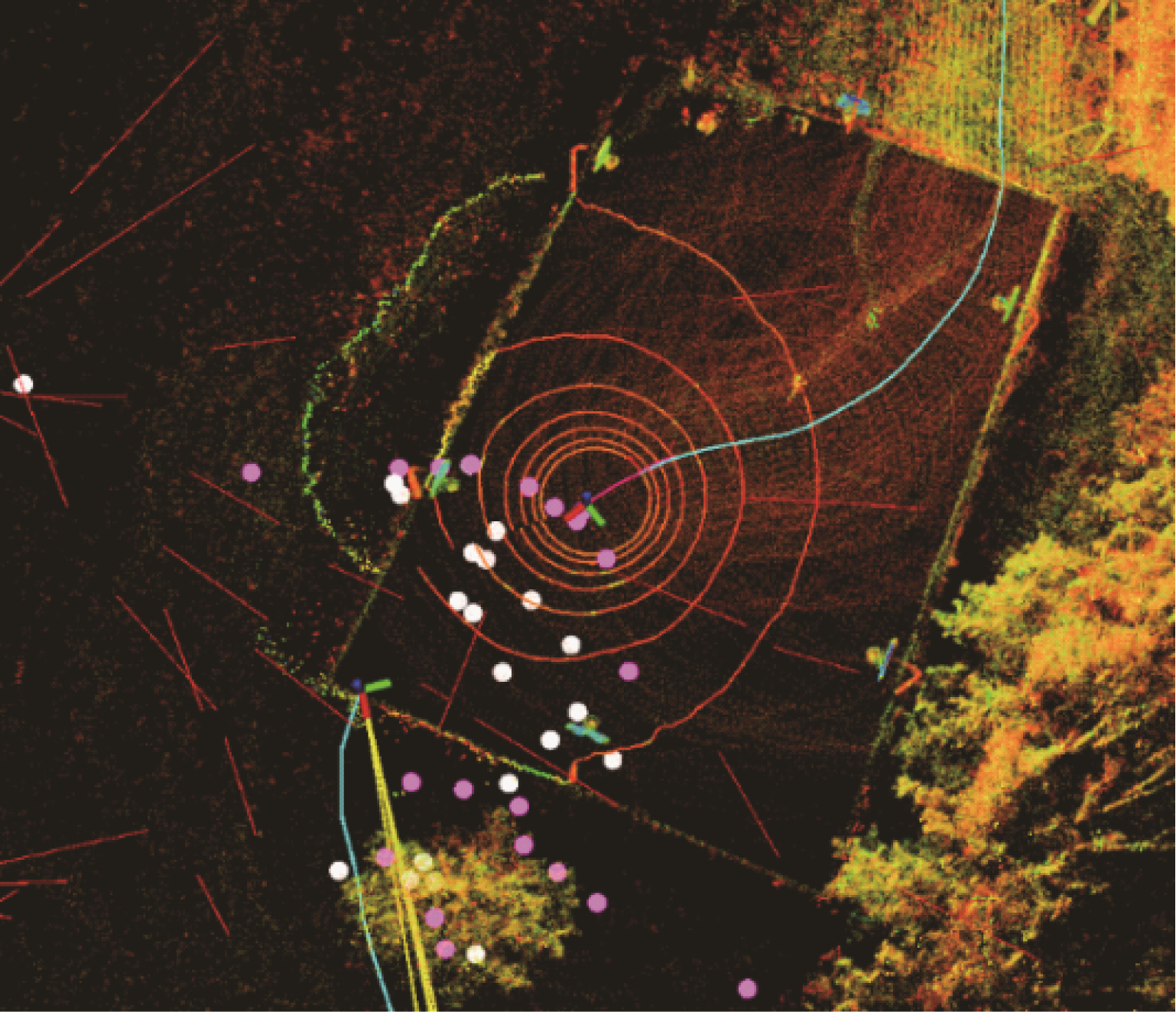
本文系统在运行jackal数据集的过程中,其三维可视化效果如图 7所示(彩色效果见《计算机工程》官网HTML版本)。其中,红色的线是三维线特征,紫色和白色的点是局部视觉特征,周围的彩色点云是不同距离上的激光雷达扫描的点云。
|
Download:
|
| 图 7 线特征三维可视化的效果 Fig. 7 Effect of 3D visualization of line features | |
在jackal数据集中,以GPS轨迹作为groundtruth,将本文系统分别和LVI-SAM、LIO-SAM及VINS-MONO系统进行轨迹对比(在进行jackal和handled数据集实验时,LIO-SAM系统和LVI-SAM系统均加了GPS因子),结果如图 8所示。

|
Download:
|
| 图 8 不同系统在jackal数据集下的轨迹对比 Fig. 8 Trajectory comparison of different systems under jackal date set | |
图 8对应的GPS轨迹中有部分震荡,原因是该部分在实际情况中受到了树木的遮挡。由图 8可以看出,VINS-MONO系统在运行一段时间后跟踪丢失,而本文系统能够有效实现位姿跟踪,且相比于LIO-SAM系统和LVI-SAM系统,本文系统的轨迹更接近GPS groundtruth。
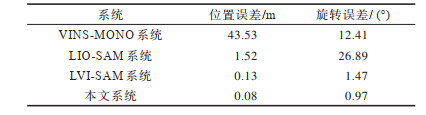
jackal数据集由移动小车收集,且起点与终点位置一样,运动稳定。本文分析了不同系统间端到端的误差,使用位置误差和旋转误差进行评估,两个误差越接近0,定位精度越高,结果如表 2所示。
|
下载CSV 表 2 不同系统的端到端误差对比 Table 2 Comparison of end-to-end error of different systems |
由表 2可知,与其他系统相比,本文系统的位置误差和旋转误差均最小。
3.3 handled数据集handled数据集是操作者手持传感器录制的,相比于jackal数据集,操作者的运动更剧烈,且有多处是退化场景。如图 9所示,当激光雷达与地面垂直或处于空旷地带时,激光雷达将无法提取足够的点云,导致扫描匹配失败,从而使里程计跟踪失败。

|
Download:
|
| 图 9 两种退化场景的示意图 Fig. 9 Schematic diagram of two degradation scenarios | |
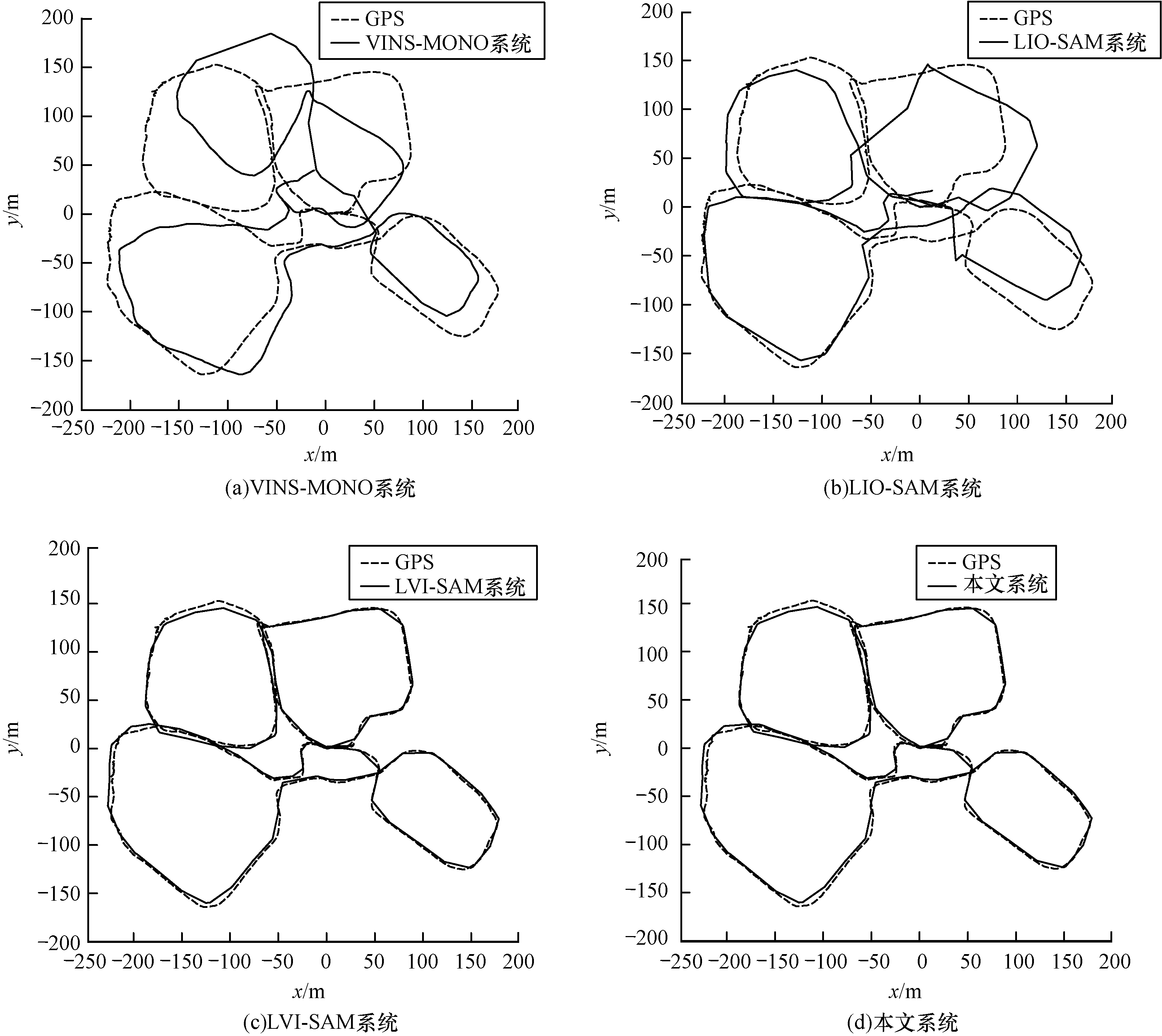
本文对比了不同系统在handled数据集下的轨迹,结果如图 10所示。由图 10可知,与其他系统相比,本文系统和LVI-SAM系统的轨迹更接近groundtruth。
|
Download:
|
| 图 10 不同系统在handled数据集下的轨迹对比 Fig. 10 Trajectory comparison of different systems under handled date set | |
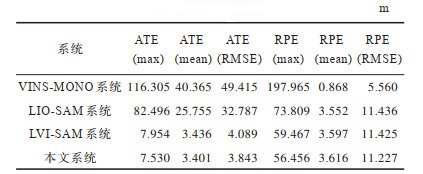
使用绝对轨迹误差(Absolute Trajectory Error,ATE)和相对轨迹误差(Relative Pose Error,RPE)中的均方根误差(Root Mean Squared Error,RMSE)来评估不同系统的全局定位精度,结果如表 3所示。
|
下载CSV 表 3 不同系统的定位精度对比 Table 3 Comparison of positioning accuracy of different systems |
由表 3可知,在有退化场景的handled数据集下,本文系统的定位精度优于其他先进的开源SLAM系统,验证了本文系统在退化场景下有更好的效果。
3.4 长走廊数据集为验证本文系统的有效性,本文录制了具有低纹理与退化场景的长走廊数据集。在长走廊的另一端,特意对传感器进行旋转,将激光雷达扫描线与地面垂直,并让相机观测低纹理区域,低纹理区域如图 11所示。

|
Download:
|
| 图 11 低纹理区域 Fig. 11 Low textured area | |
此外,本文进行了线特征匹配,结果如图 12(a)和图 12(b)所示。其中,图 12(a)对应未退化场景,图 12(b)对应低纹理退化场景,退化场景下的激光雷达扫描线是与地面垂直的。

|
Download:
|
| 图 12 低纹理场景下的线特征匹配结果 Fig. 12 Line feature matching results under low texture scenes | |
由于长走廊数据集中传感器的起始位置和终端位置一样,且终端的激光雷达坐标系在初始的激光雷达坐标系的x轴方向上旋转了180°,因此本文通过评估各个系统的端到端误差,从而进一步验证本文系统的有效性。设起点位置为(0,0,0),终点位置为(x,y,z),则终点位置与起点位置之间的误差可以使用如式(21)所示的三维空间欧氏距离表示:
| $ e\left(t\right)=\sqrt[]{{x}^{2}+{y}^{2}+{z}^{2}} $ | (21) |
角度误差为起点位置和终点位置的欧拉角之差:
| $ r\left(\boldsymbol{R}\right)={\boldsymbol{\theta }}_{\mathrm{e}\mathrm{n}\mathrm{d}}-{\boldsymbol{\theta }}_{\mathrm{b}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{n}} $ | (22) |
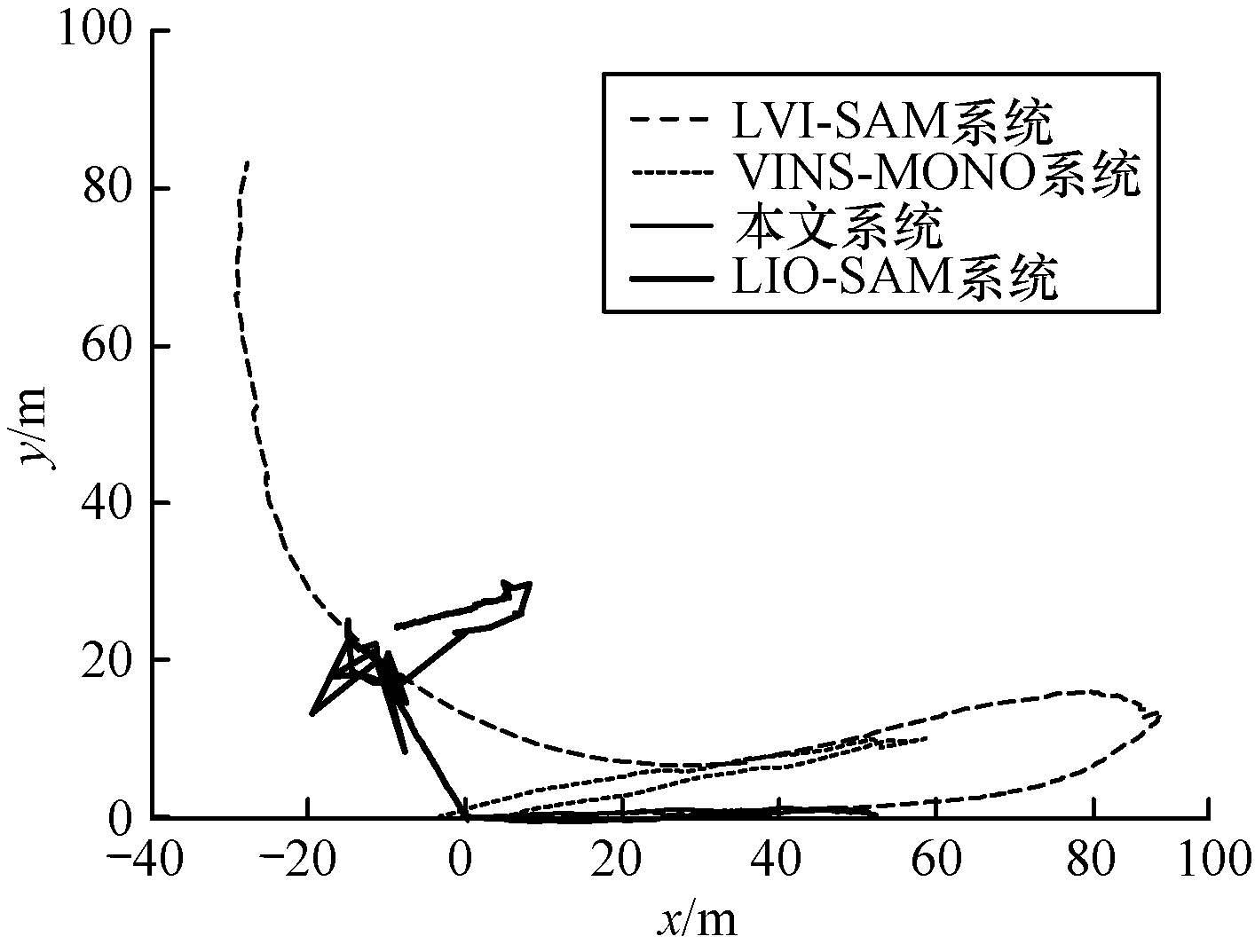
此外,在长走廊数据集下对比了各个系统的轨迹,结果如图 13所示。可以看出,本文系统可以很好地还原真实轨迹情况,能够保持起点和终点位置一致,而LVI-SAM和LIO-SAM系统在激光雷达进行垂直翻转时均发生了漂移。虽然VINS-MONO系统的轨迹完整,但在相机翻转的时候扫到了低纹理区域,其轨迹发生了偏移,导致终点和起点位置不一致。
|
Download:
|
| 图 13 不同系统在长走廊数据集下的轨迹 Fig. 13 Trajectories of different systems under long corridor data set | |
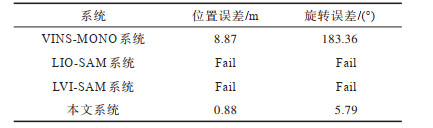
不同系统的端到端误差对比结果如表 4所示。可以看出,LIO-SAM和LVI-SAM系统的轨迹均跟踪失败。虽然VINS-MONO系统跟踪成功,但最终的位置和起点的位置相差8.87 m,角度误差为183.36°。而本文系统的位置误差仅为0.88 m,角度误差为5.79°,说明本文系统的跟踪轨迹更接近真实轨迹。
|
下载CSV 表 4 不同系统的端到端误差对比 Table 4 Comparison of end-to-end error of different system |
最后,本文采用文献[18]的耗时评估方法,在长走廊数据集下评估各系统处理一帧数据所消耗的平均时间,结果如表 5所示。可以看出,当雷达的旋转频率为10 Hz时,本文系统处理一帧数据所消耗的平均时间为56.83 ms,比LIO-SAM系统快19.22 ms。因此,本文系统更能满足实时性要求。

|
下载CSV 表 5 不同系统处理一帧数据消耗的平均时间对比 Table 5 Comparison of average time consumed by different systems to process one frame date |
本文提出一种视觉点线特征融合的激光雷达单目惯导SLAM系统。该系统主要由LIS系统及点线融合的PLVIS系统组成,2个子系统以紧耦合的方式构建了一个完整的激光雷达视觉惯性里程计,能够有效应对低纹理和退化场景。在初始化阶段,将LIS子系统的初始化成功与否作为判断依据,提升系统的鲁棒性,并在状态跟踪阶段观测线特征,提升整个系统在退化场景的跟踪能力。最后,PLVIS子系统将回环检测帧传递给LIS子系统,进一步修正系统轨迹。在jackal、handled以及自制的长走廊数据集上的实验结果表明,与VINS-MONO、LIO-SAM、LVI-SAM系统相比,本文系统具有更高的定位精度和鲁棒性。但该系统会由于场景中存在动态物体而导致相机跟踪失败。因此,下一步将考虑结合深度学习,剔除场景中的动态物体,实现更加鲁棒的位姿跟踪,使该系统适用于复杂环境。
| [1] |
CADENA C, CARLONE L, CARRILLO H, et al. Past, present, and future of simultaneous localization and mapping: toward the robust-perception age[J]. IEEE Transactions on Robotics, 2016, 32(6): 1309-1332. DOI:10.1109/TRO.2016.2624754 |
| [2] |
HUANG B C, ZHAO J, LIU J B. A survey of simultaneous localization and mapping[EB/OL]. [2021-07-01]. https://www.xueshufan.com/publication/2972879745.
|
| [3] |
WEISS S, SIEGWART R. Real-time metric state estimation for modular vision-inertial systems[C]//Proceedings of IEEE International Conference on Robotics and Automation. Washington D. C., USA: IEEE Press, 2011: 4531-4537.
|
| [4] |
KNEIP L, WEISS S, SIEGWART R. Deterministic initialization of metric state estimation filters for loosely-coupled monocular vision-inertial systems[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington D. C., USA: IEEE Press, 2011: 2235-2241.
|
| [5] |
BLOESCH M, BURRI M, OMARI S, et al. Iterated extended Kalman filter based visual-inertial odometry using direct photometric feedback[J]. The International Journal of Robotics Research, 2017, 36(10): 1053-1072. DOI:10.1177/0278364917728574 |
| [6] |
LEUTENEGGER S, LYNEN S, BOSSE M, et al. Keyframe-based visual-inertial odometry using nonlinear optimization[J]. The International Journal of Robotics Research, 2015, 34(3): 314-334. DOI:10.1177/0278364914554813 |
| [7] |
PUMAROLA A, VAKHITOV A, AGUDO A, et al. PL-SLAM: real-time monocular visual SLAM with points and lines[C]//Proceedings of IEEE International Conference on Robotics and Automation. Washington D. C., USA: IEEE Press, 2017: 4503-4508.
|
| [8] |
WEI X Y, HUANG J, MA X Y. Real-time monocular visual SLAM by combining points and lines[C]//Proceedings of IEEE International Conference on Multimedia and Expo. Washington D. C., USA: IEEE Press, 2019: 103-108.
|
| [9] |
ZHANG F K, RUI T, YANG C S, et al. LAP-SLAM: a line-assisted point-based monocular VSLAM[J]. Electronics, 2019, 8(2): 243-247. DOI:10.3390/electronics8020243 |
| [10] |
CHENG S, YANG J, KANG Z, et al. A scene-assisted point-line feature based visual slam method for autonomous flight in unknown indoor environments[J]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2019, 13: 777-783. |
| [11] |
ZUO X X, XIE X J, LIU Y, et al. Robust visual SLAM with point and line features[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington D. C., USA: IEEE Press, 2017: 1775-1782.
|
| [12] |
GOMEZ OJEDA R, MORENO F A, ZUÑIGA NOËL D, et al. PL-SLAM: a stereo SLAM system through the combination of points and line segments[J]. IEEE Transactions on Robotics, 2019, 35(3): 734-746. DOI:10.1109/TRO.2019.2899783 |
| [13] |
MUR-ARTAL R, MONTIEL J M M, TARDÓS J D. ORB-SLAM: a versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147-1163. DOI:10.1109/TRO.2015.2463671 |
| [14] |
MUR ARTAL R, TARDÓS J D. ORB SLAM2: an open-source SLAM system for monocular, stereo, and RGB-D cameras[J]. IEEE Transactions on Robotics, 2017, 33(5): 1255-1262. DOI:10.1109/TRO.2017.2705103 |
| [15] |
HE Y J, ZHAO J, GUO Y, et al. PL-VIO: tightly-coupled monocular visual-inertial odometry using point and line features[J]. Sensors, 2018, 18(4): 1159. DOI:10.3390/s18041159 |
| [16] |
FU Q, WANG J L, YU H S, et al. PL-VINS: real-time monocular visual-inertial SLAM with point and line features [EB/OL]. [2021-07-01]. https://arxiv.org/abs/2009.07462.
|
| [17] |
ZHAO S B, FANG Z, LI H L, et al. A robust laser-inertial odometry and mapping method for large-scale highway environments[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington D. C., USA: IEEE Press, 2019: 1285-1292.
|
| [18] |
SHAN T X, ENGLOT B, MEYERS D, et al. LIO-SAM: tightly-coupled lidar inertial odometry via smoothing and mapping[C]//Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems. Washington D. C., USA: IEEE Press, 2021: 5135-5142.
|
| [19] |
SHAN T X, ENGLOT B, RATTI C, et al. LVI-SAM: tightly-coupled lidar-visual-inertial odometry via smoothing and mapping[C]//Proceedings of IEEE International Conference on Robotics and Automation. Washington D. C., USA: IEEE Press, 2021: 5692-5698.
|
| [20] |
QIN T, LI P L, SHEN S J. VINS-MONO: a robust and versatile monocular visual-inertial state estimator[J]. IEEE Transactions on Robotics, 2018, 34(4): 1004-1020. DOI:10.1109/TRO.2018.2853729 |
| [21] |
GALVEZ LÓPEZ D, TARDOS J D. Bags of binary words for fast place recognition in image sequences[J]. IEEE Transactions on Robotics, 2012, 28(5): 1188-1197. DOI:10.1109/TRO.2012.2197158 |
| [22] |
LUCAS B D, KANADE T. An iterative image registration technique with an application to stereo vision [EB/OL]. [2021-07-01]. https://www.semanticscholar.org/paper/An-Iterative-Image-Registration-Technique-with-an-Lucas-Kanade/a06547951c97b2a32f23a6c2b5f79c8c75c9b9bd.
|
| [23] |
PONCE, HALL P. Multiple view geometry in computer vision[M]. Cambridge, U K: Cambridge University Press, 2003.
|
| [24] |
ZHANG L L, KOCH R. An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency[J]. Journal of Visual Communication and Image Representation, 2013, 24(7): 794-805. DOI:10.1016/j.jvcir.2013.05.006 |
| [25] |
戴志诚, 李小年, 陈增照, 等. 基于KNN算法的可变权值室内指纹定位算法[J]. 计算机工程, 2019, 45(6): 310-314. DAI Z C, LI X N, CHEN Z Z, et al. Variable-weight Indoor fingerprinting localization algorithm based on KNN algorithm[J]. Computer Engineering, 2019, 45(6): 310-314. (in Chinese) |
| [26] |
ZHANG G X, LEE J H, LIM J, et al. Building a 3D line-based map using stereo SLAM[J]. IEEE Transactions on Robotics, 2015, 31(6): 1364-1377. DOI:10.1109/TRO.2015.2489498 |
| [27] |
FORSTER C, CARLONE L, DELLAERT F, et al. On-manifold preintegration for real-time visual-inertial odometry[J]. IEEE Transactions on Robotics, 2016, 33(1): 1-21. |
| [28] |
CALONDER M, LEPETIT V, STRECHA C, et al. Brief: binary robust independent elementary features[C]//Proceedings of European Conference on Computer Vision. Berlin, Germany: Springer, 2010: 778-792.
|
| [29] |
KAESS M, JOHANNSSON H, ROBERTS R, et al. iSAM2: incremental smoothing and mapping using the bayes tree[J]. The International Journal of Robotics Research, 2012, 31(2): 216-235. DOI:10.1177/0278364911430419 |
| [30] |
ZHANG J, KAESS M, SINGH S. On degeneracy of optimization-based state estimation problems[C]//Proceedings of IEEE International Conference on Robotics and Automation. Washington D. C., USA: IEEE Press, 2016: 809-816.
|
 2022, Vol. 48
2022, Vol. 48
