开放科学(资源服务)标志码(OSID):
随着人工智能技术的快速发展,各种智能驾驶应用通过深度卷积网络的实时推断提高车辆驾驶的安全性[1-2]和效率[3-4],但是车载终端计算资源有限,难以承担深度卷积网络推断的计算开销[5]。为了减少车辆计算负荷,车联网(Internet of Vehicle,IoV)边缘计算通过在路侧部署边缘服务器,就近为车辆提供丰富的计算资源[6],然而车辆采集的数据量庞大,传输到边缘服务器进行推断处理需要消耗巨大的带宽资源,导致服务应用的时延过高[7]。为此,研究人员提出车路协同推断架构,旨在联合车载终端与边缘服务器进行推断运算,从而提高推断效率[8]。具体地,深度卷积网络被切分成两部分,依次由车载终端和边缘服务器运行[9]。车载终端上传前半部分网络的计算结果(即中间数据)至边缘服务器接力处理,边缘服务器得到最终的结果并返回至车辆[10]。车路协同推断主要有3个优势:前半部分网络一般为特征提取网络,计算开销较小,适合车载终端执行[11];中间数据远小于原始图像,传输过程的通信量明显减少[12];车载终端保留原始数据,在一定程度上保护了数据隐私[13]。
然而,针对现有车路协同推断架构,攻击者可能根据上传的中间数据复原车载终端的原始图像,从而泄露用户隐私[14]。为了防御图像还原攻击,文献[15-16]选择更深的深度卷积网络层作为切割点,减少中间数据的信息量,降低图像复原效果。文献[17]在输出的中间数据中添加随机噪声,从而干扰图像还原。这些防御方法需要通过总结大量实验的经验,在实际应用中可操作性不强,同时主要针对白盒攻击,即假设已知车载终端的深度卷积网络结构和参数,无法很好地适配实际应用情况。
本文研究车路协同推断的黑盒图像还原攻击并提出3种防御算法,分别在车载终端深度卷积网络的模型参数、输入图像、输出结果中添加随机噪声,干扰黑盒攻击者对图像的复原,同时对于3种防御算法进行差分隐私理论分析及性能评估。
1 车路协同推断的隐私泄露问题 1.1 车路协同推断架构如图 1所示,车路协同推断架构由车载终端、边缘服务器以及深度卷积网络组成。以路标识别应用为例,车载终端设备利用深度卷积网络推断,对车载摄像头拍摄到的路标图像进行类型识别。深度卷积网络被切分成两部分:前半部分
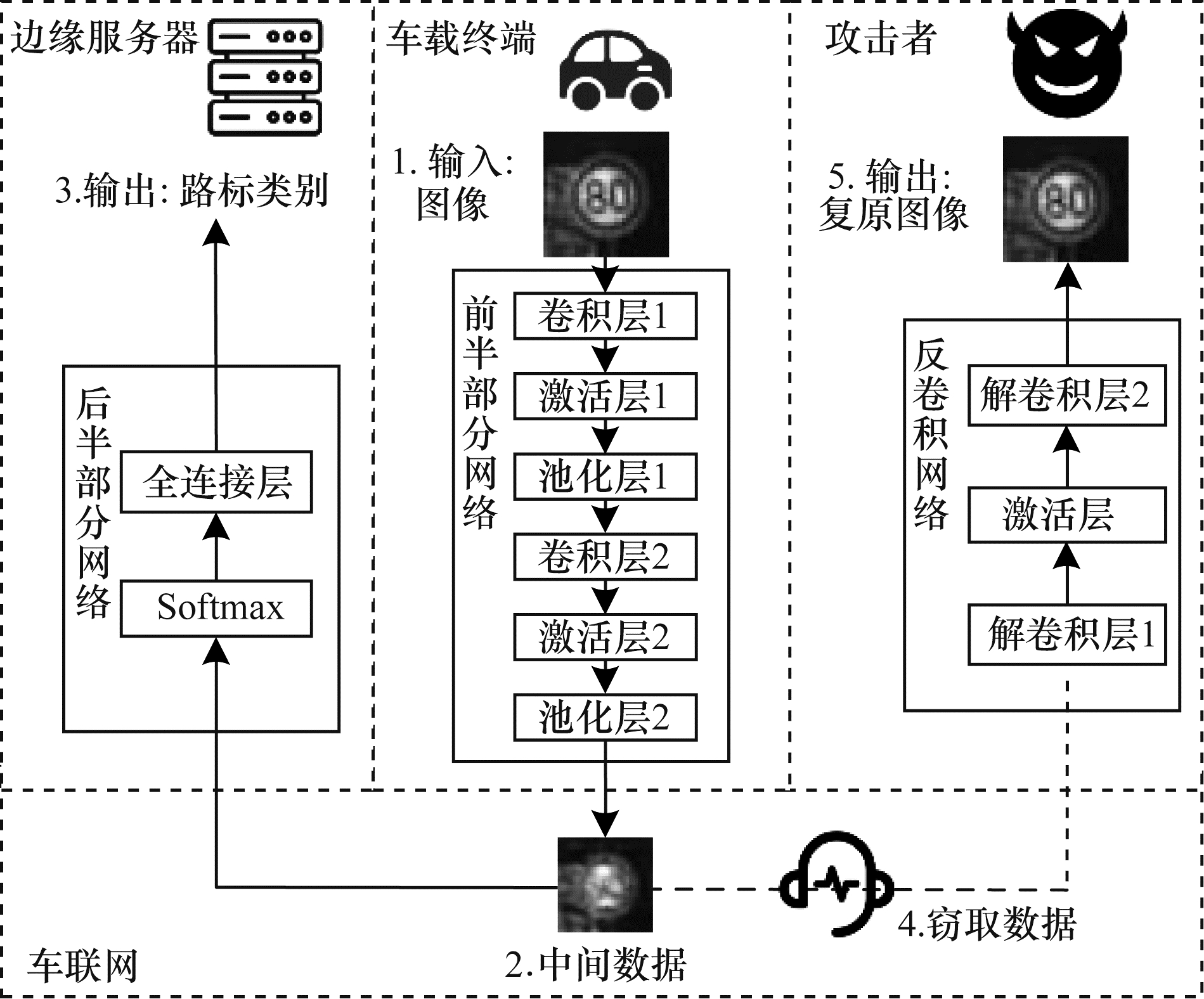
|
Download:
|
| 图 1 车路协同推断架构 Fig. 1 Collaborative vehicle-road inference architecture | |
在车路协同推断中,攻击者可能是开放环境下的窃听者,从车联网通信中窃取车载终端上传的中间数据以复原原始图像,泄露用户隐私。假设攻击者不知道车载终端设备存储的前半部分网络
在黑盒攻击的假设下,本文采用反卷积网络算法[14],通过训练一个反卷积网络,学习中间结果和原始图像之间的关系。
算法1 反卷积网络算法
输入 图像集合
输出 复原图像
1.输入
2.初始化反卷积网络
3.for
4.切分
5.for
6.更新反卷积网络参数
7.end for
8.end for
9.输入
10.return
算法1包含3个阶段:1)查询阶段,攻击者使用图像集合
| $ l\left(\omega ;X\right)=\frac{1}{n}\sum\limits_{i=1}^{n}{‖{g}_{\omega }\left({f}_{{\theta }_{1}}\right({x}_{i}\left)\right)-{x}_{i}‖}_{2}^{2} $ | (1) |
差分隐私是数据分析和机器学习中定义隐私保护程度的一种数学范式[18-19]。
定义1 当给定的两个相邻数据集
| $ \mathrm{P}\mathrm{r}\left(M\left(D\right)\in S\right) < {\mathrm{e}}^{\varepsilon }\mathrm{P}\mathrm{r}\left(M\left(D{'}\right)\in S\right) $ | (2) |
其中:
常见的隐私保护方法是在算法输出分布中加入随机噪声进行扰动[21],如拉普拉斯噪声[22]。如果要保证算法满足
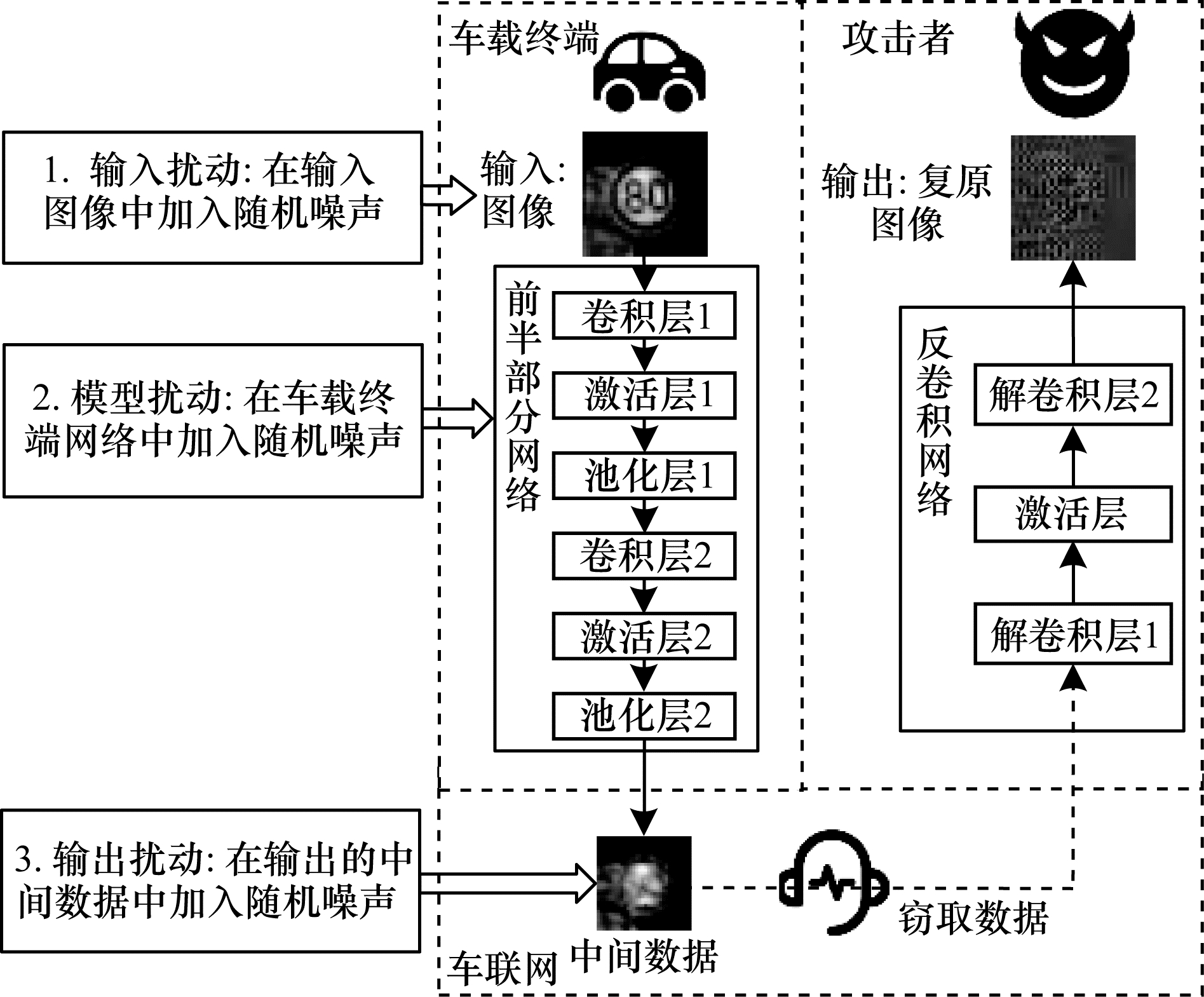
本文提出3种差分隐私防御机制,即模型扰动、输入扰动、输出扰动。如图 2所示,分别在车载终端网络的模型参数、输入图像和输出数据中加入拉普拉斯噪声扰动,影响攻击者复原的图像质量。
|
Download:
|
| 图 2 车路协同推断的差分隐私保护过程 Fig. 2 Process of differential privacy protection for collaborative vehicle-road inference | |
模型扰动机制的具体流程如算法2所示。首先,将所有模型参数的大小限制在阈值
算法2 模型扰动算法
输入 图像集合
输出 模型扰动后的输出结果
步骤1 限制模型参数大小
步骤2 在模型参数中注入噪声
步骤3 计算经模型扰动后的输出结果
输入扰动机制的具体流程如算法3所示。首先,限制输入图像像素值在阈值
算法3 输入扰动算法
输入 图像集合
输出 输入扰动后的输出结果
步骤1 限制输入图像大小
步骤2 在输入图像中注入噪声
步骤3 计算经输入扰动后的输出结果
输出扰动机制的具体流程如算法4所示。首先,推断得到中间数据
算法4 输出扰动算法
输入 图像集合
输出 模型扰动后的输出结果
步骤1 计算输出结果
步骤2 限制输出结果大小
步骤3 对输出结果注入噪声
上述3种算法是在车载终端执行模型推断的过程中,分别对模型参数、输入图像、输出结果执行添加随机拉普拉斯噪声的操作。因此,算法的复杂度与深度模型本身的计算无关,而与添加噪声的对象维度有关。显然,输出结果维度最小,其次输入图像,模型参数维度最大。因此,输出扰动算法复杂度最低,其次输入扰动算法,模型扰动算法复杂度最高。
2.3 隐私保护分析定理1 给定输入图像集合
证明 给定任意相邻输入
| $ {\varDelta }_{\mathrm{M}}=\underset{X, X{'}}{\mathrm{m}\mathrm{a}\mathrm{x}}{‖{\theta }_{1}-\overline{{\theta }_{1}}‖}_{1}\le 2{C}_{\mathrm{M}} $ | (3) |
计算得到:
| $ \begin{array}{l}\frac{\mathrm{P}\mathrm{r}\left[{f}_{{\theta }_{1}+\mathrm{L}\mathrm{a}\mathrm{p}\left(0, \frac{2{C}_{\mathrm{M}}}{\varepsilon }\right)}\left(X\right)=S\right]}{\mathrm{P}\mathrm{r}\left[{f}_{{\theta }_{1}+\mathrm{L}\mathrm{a}\mathrm{p}\left(0, \frac{2{C}_{\mathrm{M}}}{\varepsilon }\right)}\left(X{'}\right)=S\right]}=\frac{{\mathrm{e}}^{-\frac{\varepsilon }{2{C}_{\mathrm{M}}}\left|{\theta }_{1}\right|}}{{\mathrm{e}}^{-\frac{\varepsilon }{2{C}_{\mathrm{M}}}\left|\overline{{\theta }_{1}}\right|}}=\\ {\mathrm{e}}^{\frac{\varepsilon }{2{C}_{\mathrm{M}}}\left(\left|{\theta }_{1}\right|-\left|\overline{{\theta }_{1}}\right|\right)}\le {\mathrm{e}}^{\frac{\varepsilon }{2{C}_{\mathrm{M}}}\left|{\theta }_{1}-\overline{{\theta }_{1}}\right|}\le {\mathrm{e}}^{\varepsilon }\end{array} $ | (4) |
因此,根据定义1,当噪声尺度
定理2 给定输入图像集合
证明 因为输入图像像素值在范围
| $ {\varDelta }_{\mathrm{I}}=\underset{X, X{'}}{\mathrm{m}\mathrm{a}\mathrm{x}}{‖X-X{'}‖}_{1}\le 2{C}_{\mathrm{I}} $ | (5) |
计算得到:
| $ \begin{array}{l}\frac{\mathrm{P}\mathrm{r}\left[{f}_{{\theta }_{1}}\left(X+\mathrm{L}\mathrm{a}\mathrm{p}\left(0, \frac{2{C}_{\mathrm{I}}}{\varepsilon }\right)\right)=S\right]}{\mathrm{P}\mathrm{r}\left[{f}_{{\theta }_{1}}\left(X{'}+\mathrm{L}\mathrm{a}\mathrm{p}\left(0, \frac{2{C}_{\mathrm{I}}}{\varepsilon }\right)\right)=S\right]}=\frac{{\mathrm{e}}^{-\frac{\varepsilon }{2{C}_{\mathrm{I}}}\left|X\right|}}{{\mathrm{e}}^{-\frac{\varepsilon }{2{C}_{\mathrm{I}}}\left|X{'}\right|}}=\\ {\mathrm{e}}^{\frac{\varepsilon }{2{C}_{\mathrm{I}}}\left(\left|X\right|-\left|X{'}\right|\right)}\le {\mathrm{e}}^{\frac{\varepsilon }{2{C}_{\mathrm{I}}}\left|X-X{'}\right|}\le {\mathrm{e}}^{\varepsilon }\end{array} $ | (6) |
因此,根据定义1,当噪声尺度
定理3 给定输入图像
证明 因为计算结果元素值限制在范围
| $ {\varDelta }_{\mathrm{O}}=\underset{X, X{'}}{\mathrm{m}\mathrm{a}\mathrm{x}}{‖{f}_{{\theta }_{1}}\left(X\right)-{f}_{{\theta }_{1}}\left(X{'}\right)‖}_{1}\le 2{C}_{\mathrm{O}} $ | (7) |
计算得到:
| $ \begin{array}{l}\frac{\mathrm{P}\mathrm{r}\left[{f}_{{\theta }_{1}}\left(X\right)+\mathrm{L}\mathrm{a}\mathrm{p}\left(0, \frac{2{C}_{\mathrm{O}}}{\varepsilon }\right)=S\right]}{\mathrm{P}\mathrm{r}\left[{f}_{{\theta }_{1}}\left(X{'}\right)+\mathrm{L}\mathrm{a}\mathrm{p}\left(0, \frac{2{C}_{\mathrm{O}}}{\varepsilon }\right)=S\right]}=\frac{{\mathrm{e}}^{-\frac{\varepsilon }{2{C}_{\mathrm{O}}}\left|{f}_{{\theta }_{1}}\left(X\right)\right|}}{{\mathrm{e}}^{-\frac{\varepsilon }{2{C}_{\mathrm{O}}}\left|{f}_{{\theta }_{1}}\left(X{'}\right)\right|}}=\\ {\mathrm{e}}^{\frac{\varepsilon }{2{C}_{\mathrm{O}}}\left(\left|{f}_{{\theta }_{1}}\left(X\right)\right|-\left|{f}_{{\theta }_{1}}\left(X{'}\right)\right|\right)}\le {\mathrm{e}}^{\frac{\varepsilon }{2{C}_{\mathrm{O}}}\left|{f}_{{\theta }_{1}}\left(X\right)-{f}_{{\theta }_{1}}\left(X{'}\right)\right|}\le {\mathrm{e}}^{\varepsilon }\end{array} $ | (8) |
因此,根据定义1,当噪声尺度
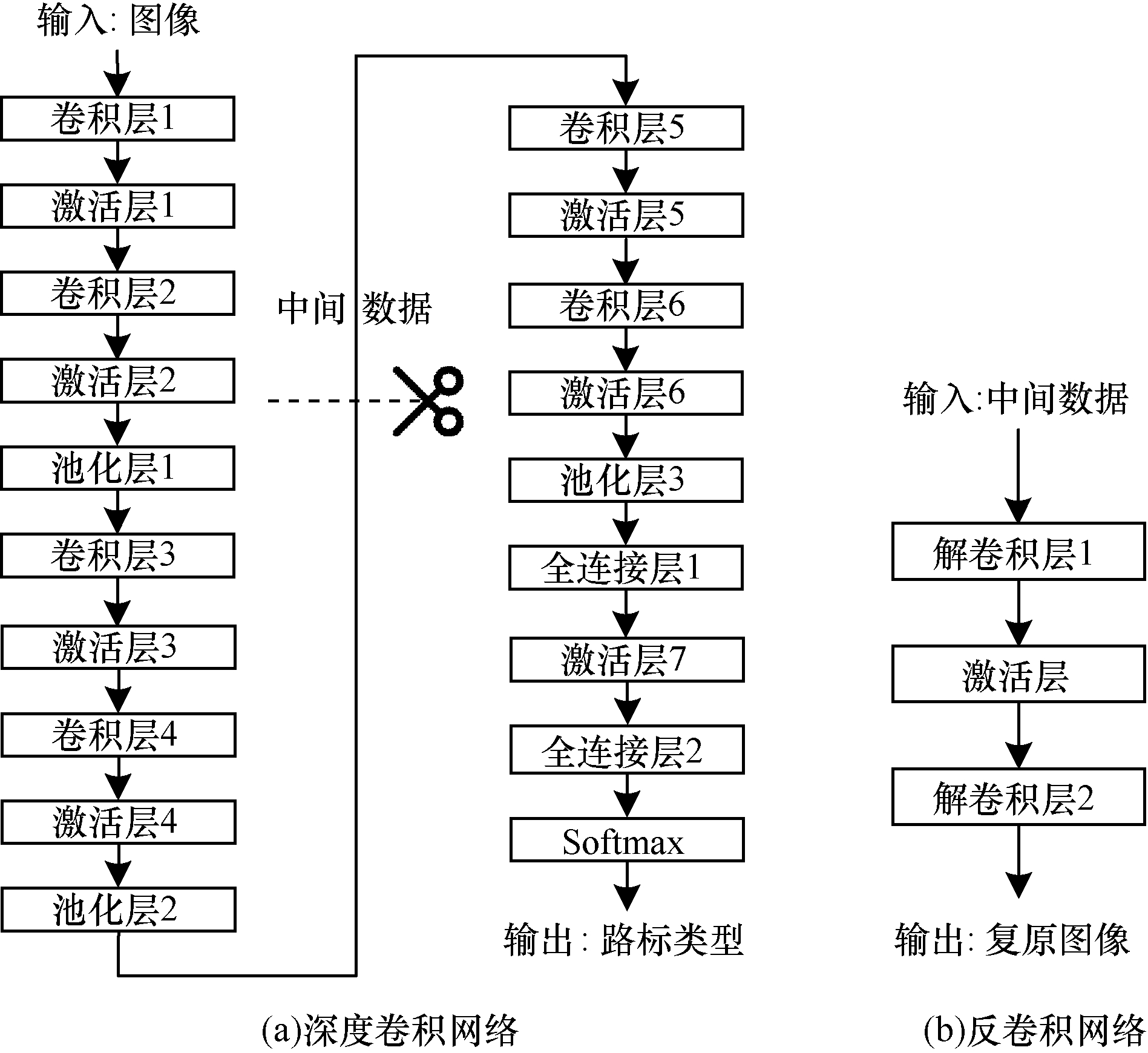
实验使用GTSRB数据集[24],该数据集用于路标识别任务,由39 208个训练样本和12 630个测试样本组成。如图 3所示,实验所用的深度卷积网络由6个卷积层和2个全连接层组成。每个卷积层有32个通道,核大小为3,并使用ReLU函数作为激活函数。每2个卷积层后面连接1个池化层。考虑车路协同推断选择第2个池化层作为切分点。攻击者采用的反卷积网络由2个解卷积层和1个激活层组成。深度卷积网络和反卷积网络的训练均采用ADAM优化器,学习率为0.001。
|
Download:
|
| 图 3 深度卷积网络与反卷积网络结构 Fig. 3 Structure of deep convolutional network and deconvolutional network | |
假设A和B为原始图像和复原图像,大小为
1)均方误差(Mean Squared Error,MSE),以两张图像像素值的均方差衡量两张图像的相似度。MSE越小,两张图像的相似度越高。MSE定义如下:
| $ \mathrm{M}\mathrm{S}\mathrm{E}\left(A, B\right)=\frac{1}{mn}\sum\limits_{i, j=\mathrm{1, 1}}^{m, n}{‖A\left(i, j\right)-B\left(i, j\right)‖}^{2} $ | (9) |
2)结构相似度(Structural Similarity,SSIM),根据两张图像的结构信息衡量相似度,取值范围为
| $ \mathrm{S}\mathrm{S}\mathrm{I}\mathrm{M}\left(A, B\right)=\frac{\left(2{\mu }_{A}{\mu }_{B}+{c}_{1}\right)\left(2{\sigma }_{AB}+{c}_{2}\right)}{\left({\mu }_{A}^{2}+{\mu }_{B}^{2}+{c}_{1}\right)\left({\sigma }_{A}^{2}+{\sigma }_{B}^{2}+{c}_{2}\right)} $ | (10) |
3)峰值信噪比(Peak Signal-to-Noise Ratio,PSNR),基于对应像素点的峰值误差来衡量相似度。PSNR越大,两张图像相似度越高。PSNR定义如下:
| $ \mathrm{P}\mathrm{S}\mathrm{N}\mathrm{R}\left(A, B\right)=10\mathrm{l}\mathrm{g}\left(\frac{{255}^{2}}{\mathrm{M}\mathrm{S}\mathrm{E}\left(A, B\right)}\right) $ | (11) |
对比3种差分隐私防御算法与选择切点防御法对图像还原攻击的防御效果。选择切点防御法主张选择更深的网络层作为切割点切分深度卷积网络,使得攻击者复原效果变差[15-16]。
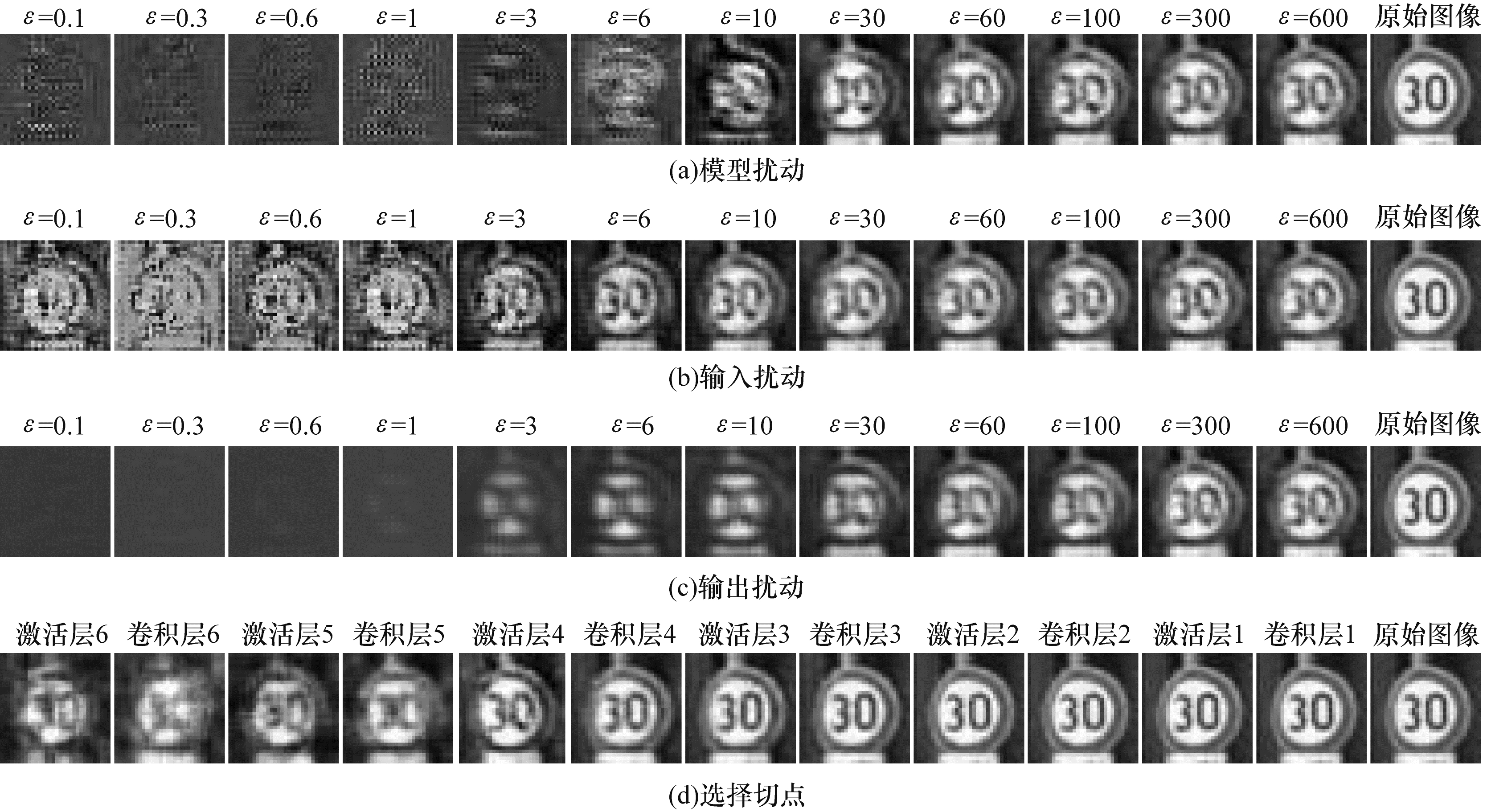
图 4给出了在使用不同防御算法时,攻击者使用还原攻击复原的图像。模型扰动算法的防御效果最好,在隐私预算
|
Download:
|
| 图 4 不同防御算法保护下的复原图像 Fig. 4 Recovered images protected by different defense algorithms | |
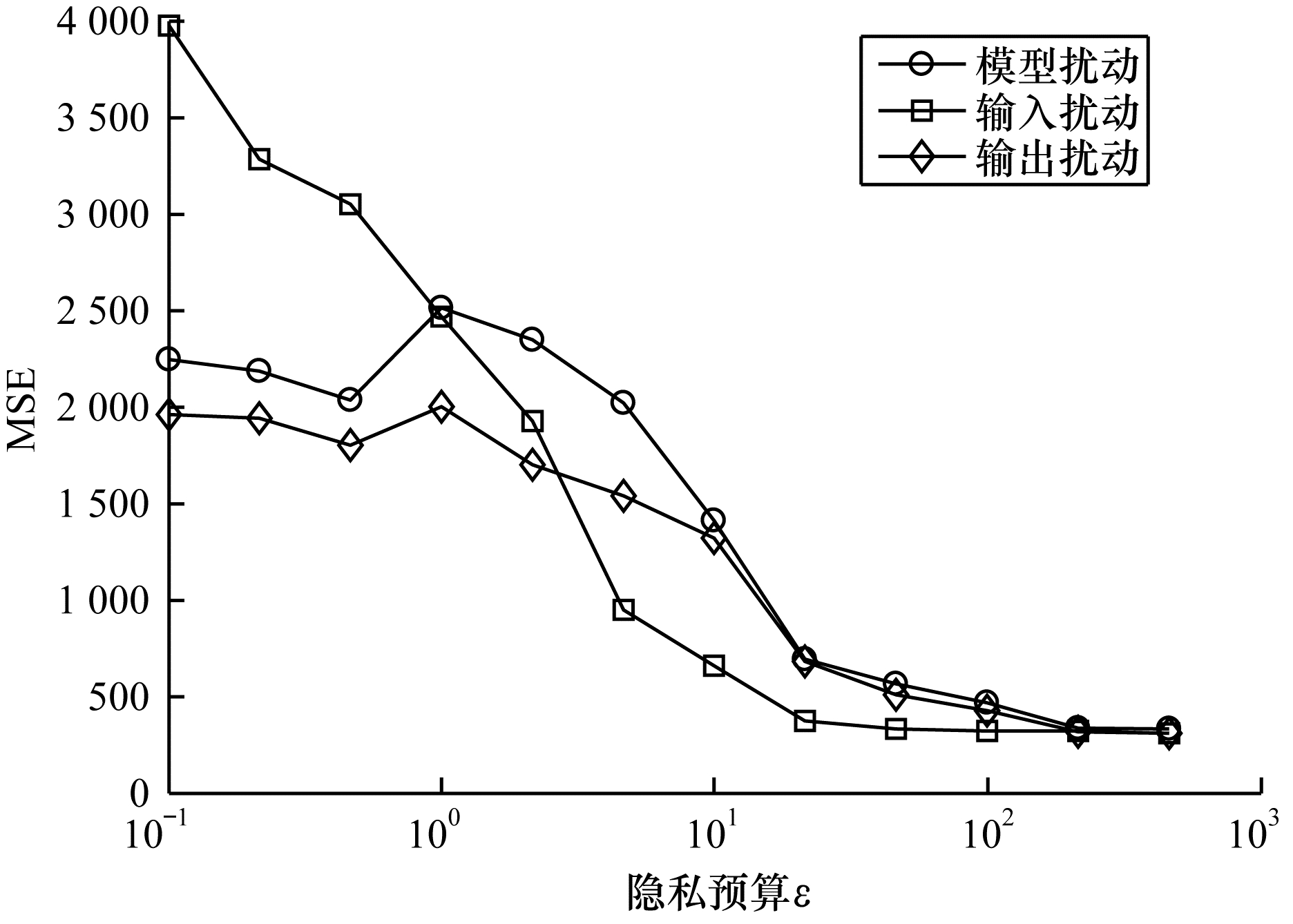
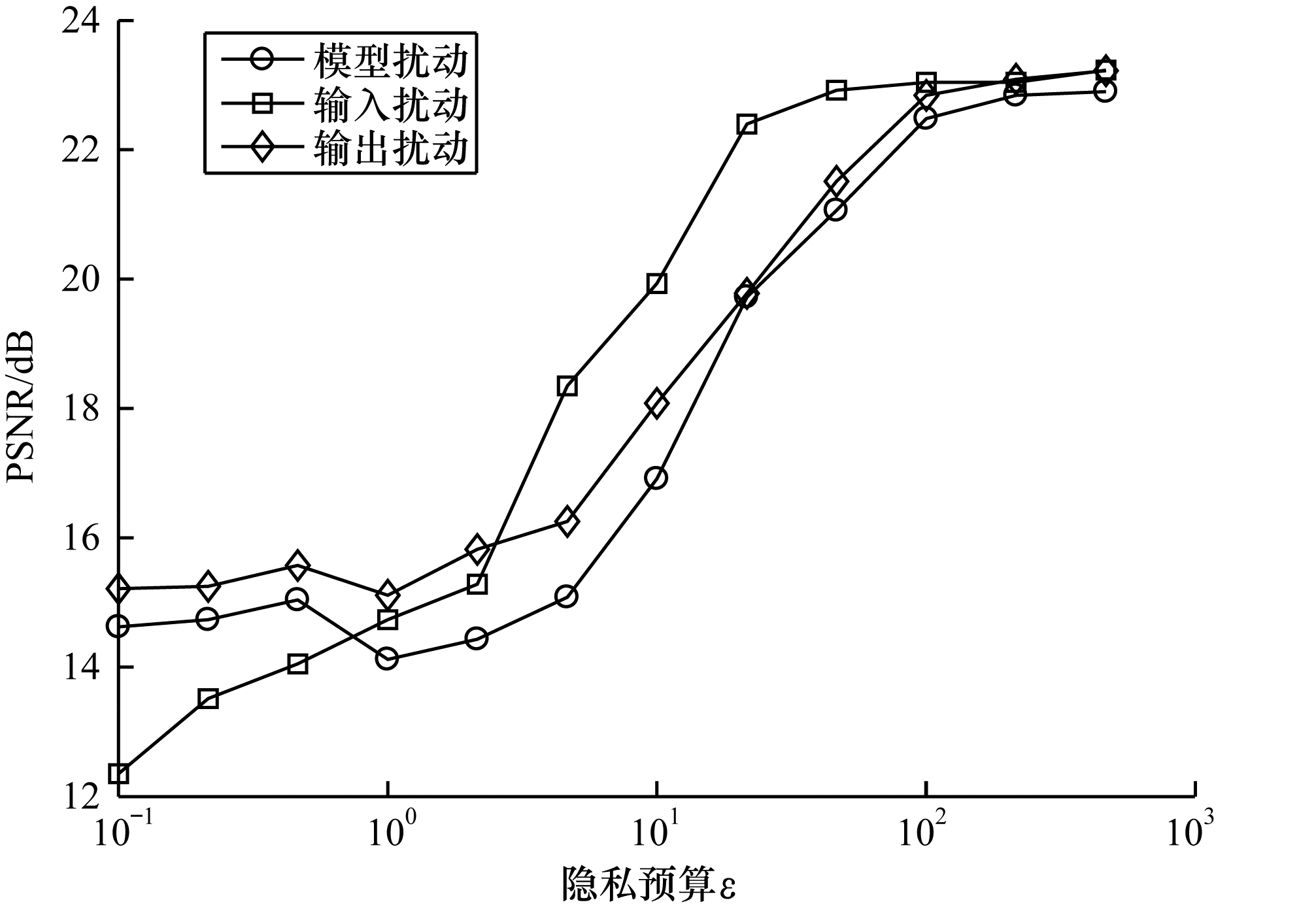
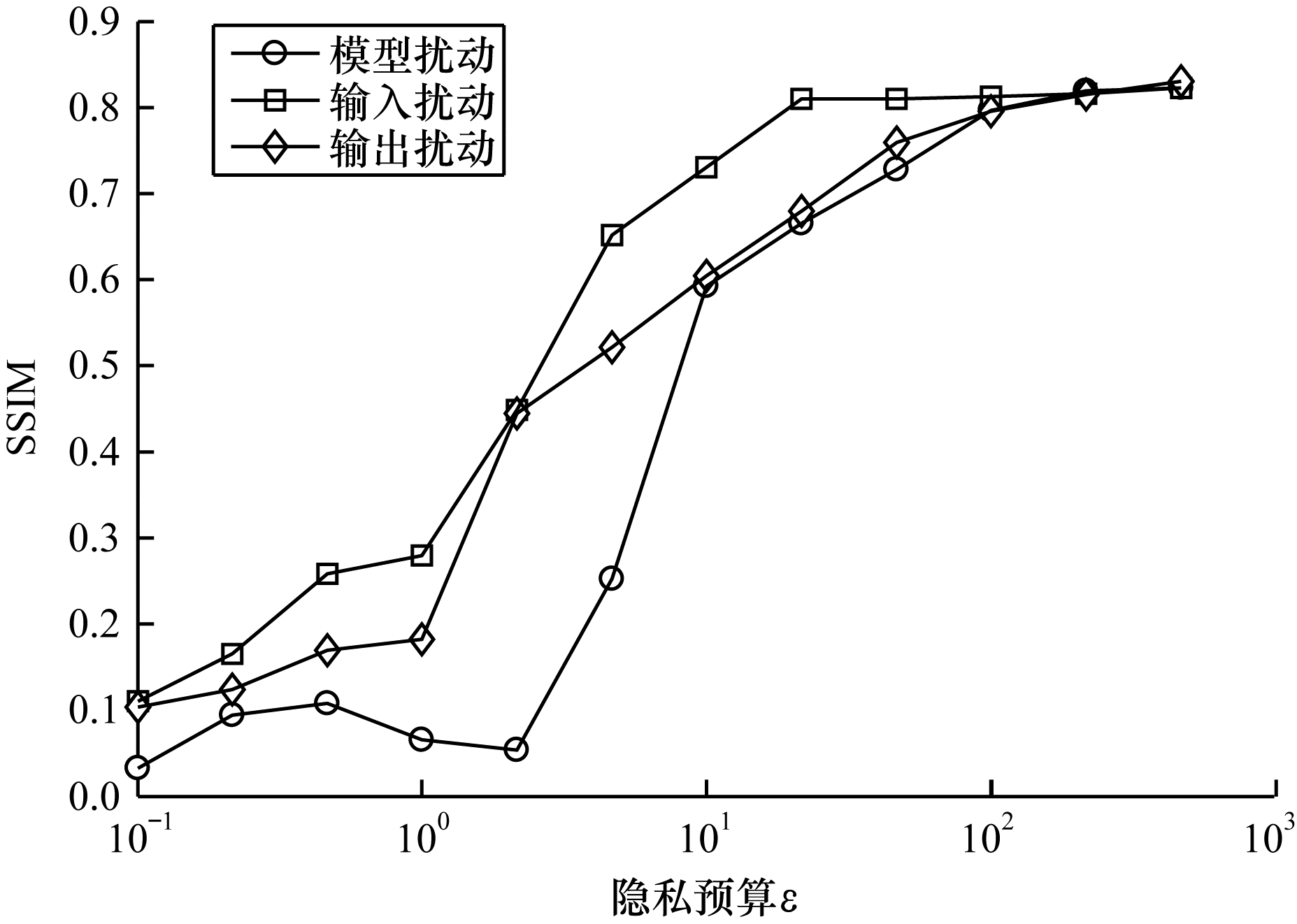
图 5、图 6和图 7分别给出了对于不同的隐私预算,在3种防御算法干扰下复原图像的MSE、PSNR和SSIM。模型扰动算法的防御效果明显最优,在其干扰下的图像还原质量最低,其次是输出扰动算法,最后是输入扰动算法。但是当
|
Download:
|
| 图 5 不同隐私预算对应的复原图像MSE Fig. 5 MSE of recovered images corresponding to different privacy budgets | |
|
Download:
|
| 图 6 不同隐私预算对应的复原图像PSNR Fig. 6 PSNR of recovered images corresponding to different privacy budgets | |
|
Download:
|
| 图 7 不同隐私预算对应的复原图像SSIM Fig. 7 SSIM of recovered images corresponding to different privacy budgets | |
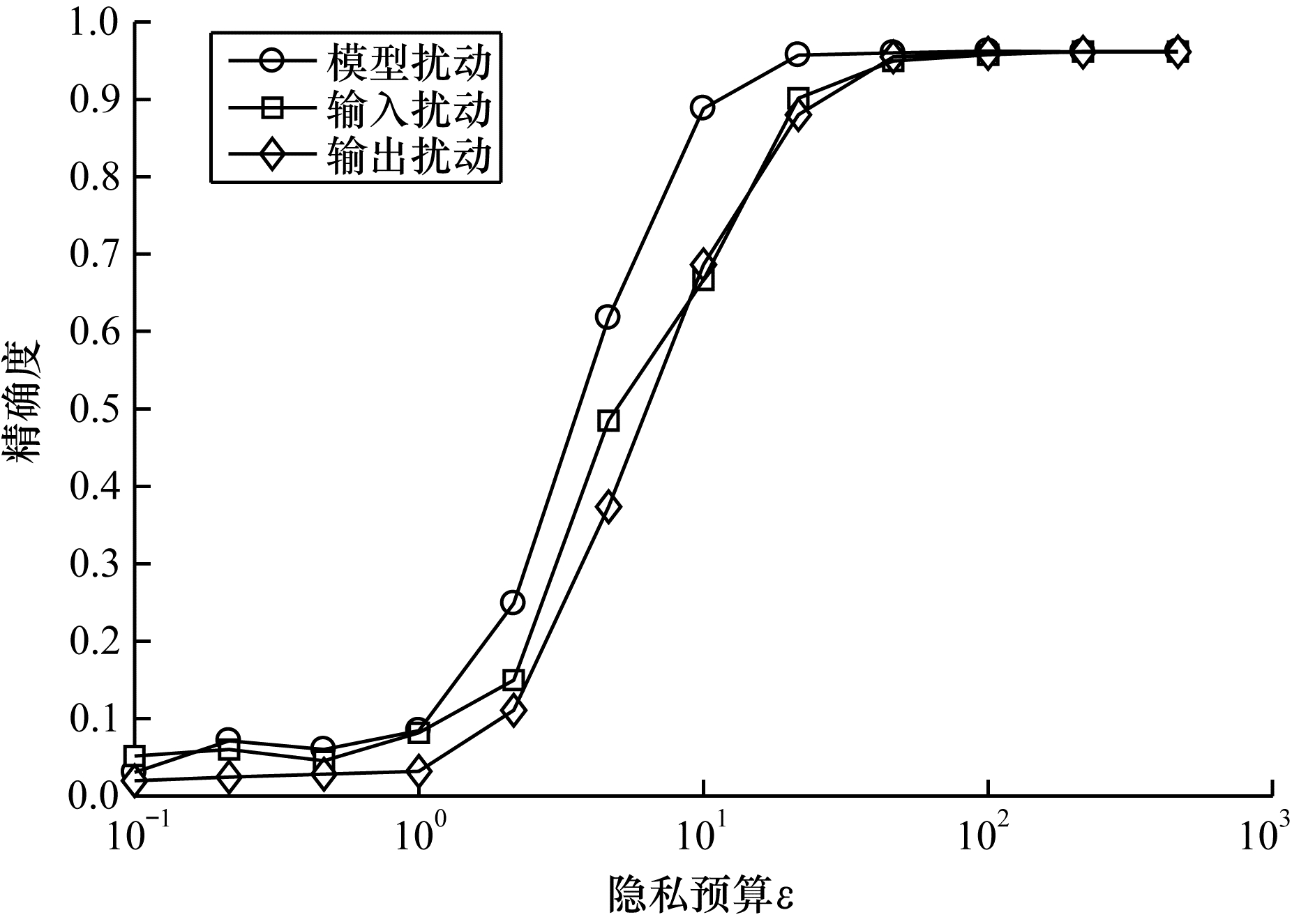
图 8表示不同隐私预算对推断精确度的影响。当
|
Download:
|
| 图 8 不同隐私预算对推断精确度的影响 Fig. 8 Impact of different accuracy budgets on inference accuracy | |
图 9、图 10表示推断精确度和还原图像质量之间的关系。当PSNR和SSIM越小,推断精确度越低,即还原图像质量越差时,对黑盒图像还原攻击防御效果越好,同时对深度卷积网络模型的推断精确度影响也越大。在达到相同的防御效果时,模型扰动算法达到的推断精确度最高,其次是输出扰动算法,最后是输入扰动算法。因此,在3种差分隐私保护算法中,模型扰动算法在均衡隐私保护和推断精确度方面获得最优效果。
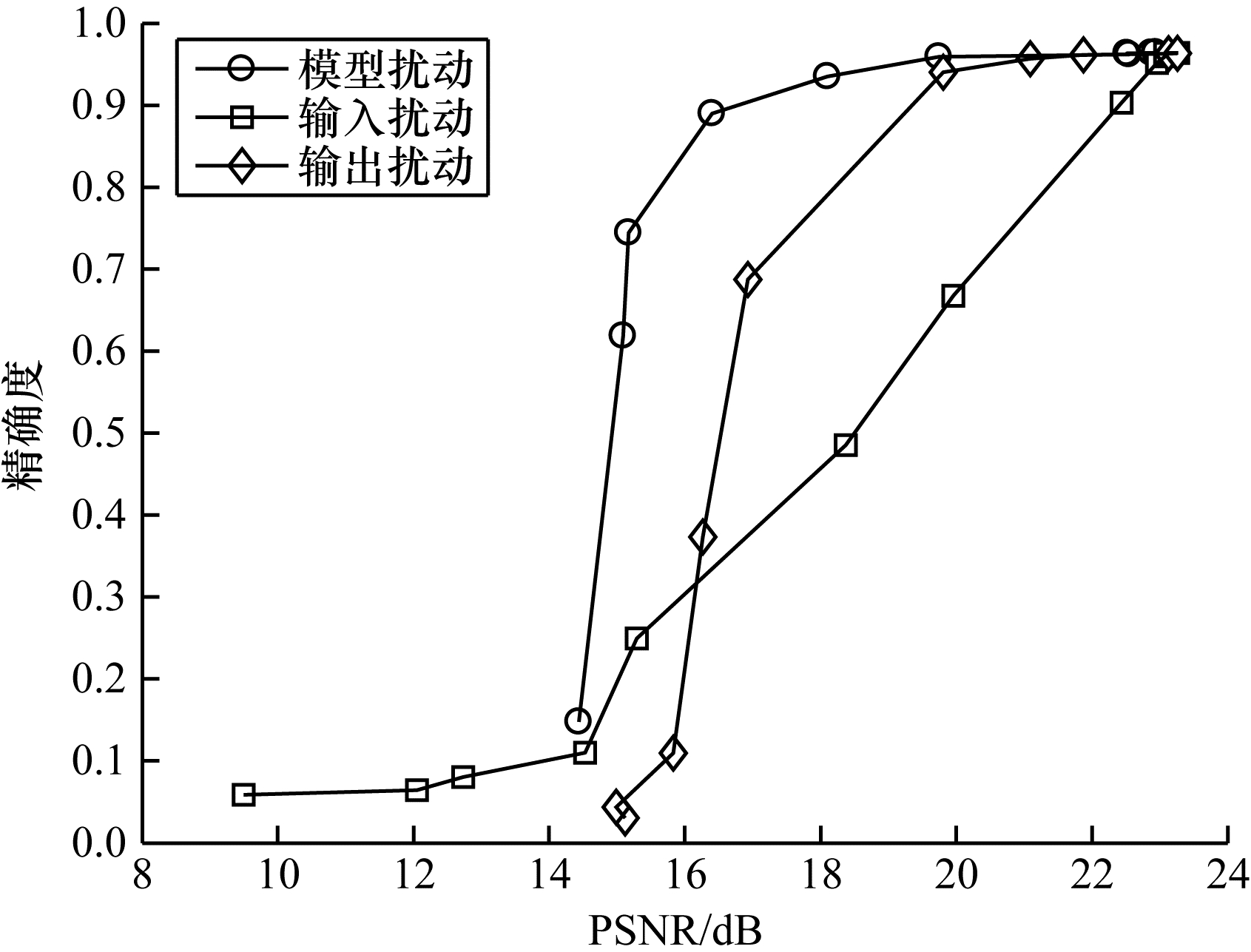
|
Download:
|
| 图 9 推断精确度与PSNR的关系 Fig. 9 Relationship between inference accuracy and PSNR | |
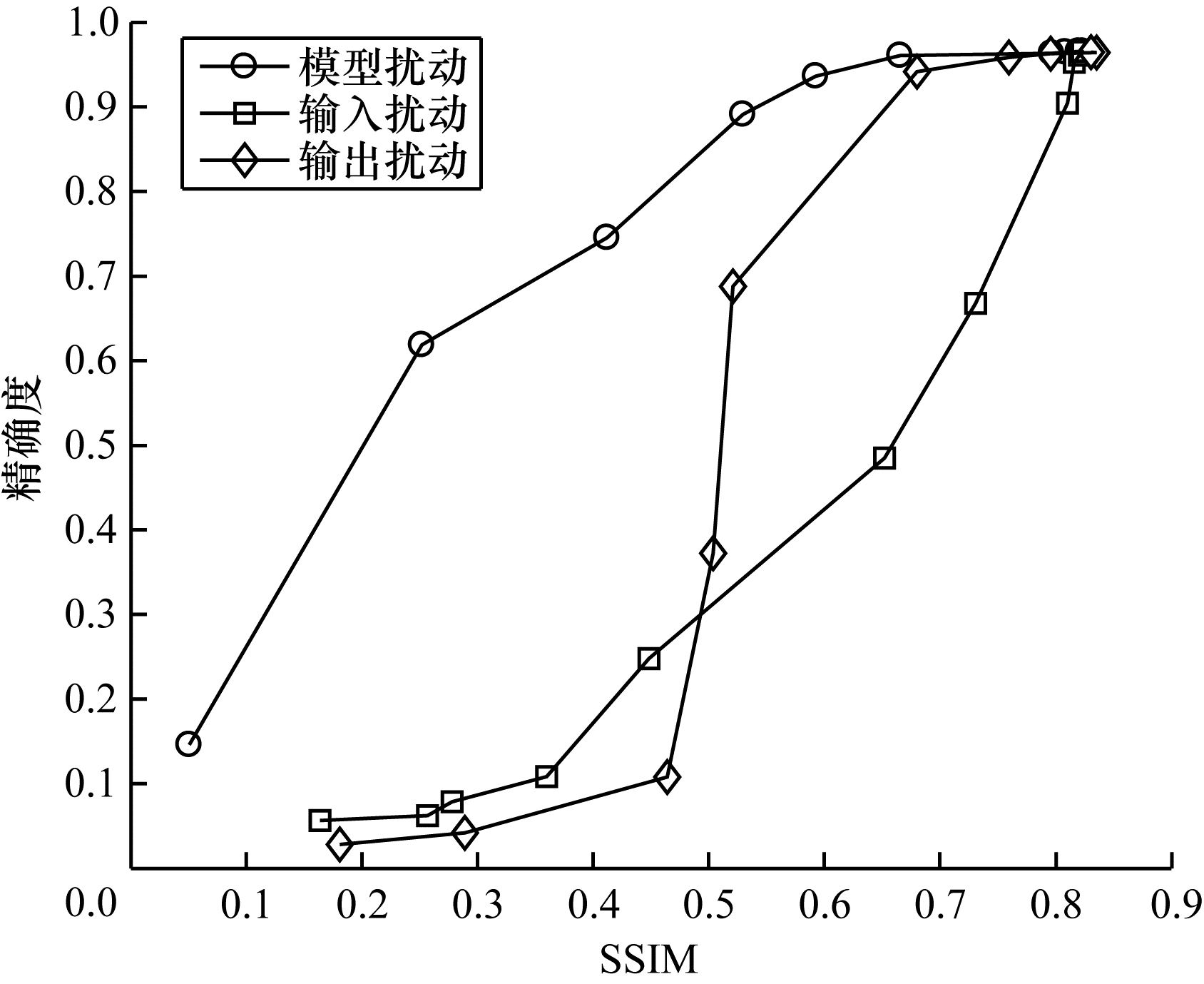
|
Download:
|
| 图 10 推断精确度与SSIM的关系 Fig. 10 Relationship between inference accuracy and SSIM | |
本文针对车路协同推断中的黑盒图像还原攻击,提出3种基于差分隐私的防御算法,分别在车载终端深度卷积网络的模型参数、输入图像、输出结果中注入随机生成的拉普拉斯噪声。通过理论分析得出3种算法均满足
| [1] |
HUANG X M, YU R, YE D D, et al. Efficient workload allocation and user-centric utility maximization for task scheduling in collaborative vehicular edge computing[J]. IEEE Transactions on Vehicular Technology, 2021, 70(4): 3773-3787. DOI:10.1109/TVT.2021.3064426 |
| [2] |
LIM W Y B, HUANG J Q, XIONG Z H, et al. Towards federated learning in UAV-enabled Internet of vehicles: a multi-dimensional contract-matching approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2021, 22(8): 5140-5154. DOI:10.1109/TITS.2021.3056341 |
| [3] |
GRIGORESCU S, TRASNEA B, COCIAS T, et al. A survey of deep learning techniques for autonomous driving[J]. Journal of Field Robotics, 2020, 37(3): 362-386. DOI:10.1002/rob.21918 |
| [4] |
MUHAMMAD K, ULLAH A, LLORET J, et al. Deep learning for safe autonomous driving: current challenges and future directions[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 22(7): 4316-4336. |
| [5] |
WU M Q, HUANG X M, TAN B H, et al. Hybrid sensor network with edge computing for AI applications of connected vehicles[J]. Journal of Internet Technology, 2020, 21: 1503-1516. |
| [6] |
LIU L, CHEN C, PEI Q Q, et al. Vehicular edge computing and networking: a survey[J]. Mobile Networks and Applications, 2021, 26(3): 1145-1168. DOI:10.1007/s11036-020-01624-1 |
| [7] |
LIU Y J, WANG S G, ZHAO Q L, et al. Dependency-aware task scheduling in vehicular edge computing[J]. IEEE Internet of Things Journal, 2020, 7(6): 4961-4971. DOI:10.1109/JIOT.2020.2972041 |
| [8] |
ZHANG J, LETAIEF K B. Mobile edge intelligence and computing for the Internet of vehicles[J]. Proceedings of the IEEE, 2020, 108(2): 246-261. DOI:10.1109/JPROC.2019.2947490 |
| [9] |
KANG Y P, HAUSWALD J, GAO C, et al. Neurosurgeon: collaborative intelligence between the cloud and mobile edge[J]. ACM SIGPLAN Notices, 2017, 52(4): 615-629. DOI:10.1145/3093336.3037698 |
| [10] |
LI E, ZHOU Z, CHEN X. Edge intelligence: on-demand deep learning model co-inference with device-edge synergy[C]//Proceedings of 2018 Workshop on Mobile Edge Communications. New York, USA: ACM Press, 2018: 31-36.
|
| [11] |
WANG Q, LI Z Y, NAI K, et al. Dynamic resource allocation for jointing vehicle-edge deep neural network inference[J]. Journal of Systems Architecture, 2021, 117: 102133. DOI:10.1016/j.sysarc.2021.102133 |
| [12] |
TAN X R, LI H J, WANG L M, et al. End-edge coordinated inference for real-time BYOD malware detection using deep learning[C]//Proceedings of IEEE Wireless Communications and Networking Conference. Washington D. C., USA: IEEE Press, 2020: 1-6.
|
| [13] |
LI E, ZENG L K, ZHOU Z, et al. Edge AI: on-demand accelerating deep neural network inference via edge computing[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 447-457. DOI:10.1109/TWC.2019.2946140 |
| [14] |
HE Z C, ZHANG T W, LEE R B. Model inversion attacks against collaborative inference[C]//Proceedings of the 35th Annual Computer Security Applications Conference. New York, USA: ACM Press, 2019: 148-162.
|
| [15] |
SHI C S, CHEN L X, SHEN C, et al. Privacy-aware edge computing based on adaptive DNN partitioning[C]//Proceedings of IEEE Global Communications Conference. Washington D. C., USA: IEEE Press, 2019: 1-6.
|
| [16] |
HE Z C, ZHANG T W, LEE R B. Attacking and protecting data privacy in edge-cloud collaborative inference systems[J]. IEEE Internet of Things Journal, 2021, 8(12): 9706-9716. DOI:10.1109/JIOT.2020.3022358 |
| [17] |
RYU J, ZHENG Y F, GAO Y S, et al. Can differential privacy practically protect collaborative deep learning inference for the Internet of Things?[EB/OL]. [2021-08-17]. https://arxiv.org/abs/2104.03813.
|
| [18] |
ABADI M, CHU A, GOODFELLOW I, et al. Deep learning with differential privacy[C]//Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security. New York, USA: ACM Press, 2016: 308-318.
|
| [19] |
ZHAO P, ZHANG G L, WAN S H, et al. A survey of local differential privacy for securing Internet of vehicles[J]. The Journal of Supercomputing, 2020, 76(11): 8391-8412. DOI:10.1007/s11227-019-03104-0 |
| [20] |
郝晨艳, 彭长根, 张盼盼. 重复攻击下差分隐私保护参数ε的选取方法[J]. 计算机工程, 2018, 44(7): 145-149. HAO C Y, PENG C G, ZHANG P P. Selection method of differential privacy protection parameter ε under repeated attack[J]. Computer Engineering, 2018, 44(7): 145-149. (in Chinese) |
| [21] |
WU M Q, YE D D, DING J H, et al. Incentivizing differentially private federated learning: a multidimensional contract approach[J]. IEEE Internet of Things Journal, 2021, 8(13): 10639-10651. DOI:10.1109/JIOT.2021.3050163 |
| [22] |
王丹, 龙士工. 权重社交网络隐私保护中的差分隐私算法[J]. 计算机工程, 2019, 45(4): 114-118. WANG D, LONG S G. Differential privacy algorithm for privacy protection in weighted social network[J]. Computer Engineering, 2019, 45(4): 114-118. (in Chinese) |
| [23] |
NIU B, CHEN Y H, WANG B Y, et al. AdaPDP: adaptive personalized differential privacy[C]//Proceedings of IEEE Conference on Computer Communications. Washington D. C., USA: IEEE Press, 2021: 1-10.
|
| [24] |
YIN S H, DENG J C, ZHANG D W, et al. Traffic sign recognition based on deep convolutional neural network[M]. Berlin, Germany: Springer, 2017.
|
| [25] |
雷蕾, 郭东恩, 靳峰. 基于谱归一化条件生成对抗网络的图像修复算法[J]. 计算机工程, 2021, 47(1): 230-238. LEI L, GUO D E, JIN F. Image inpainting algorithm based on conditional generative adversarial network with spectral normalization[J]. Computer Engineering, 2021, 47(1): 230-238. (in Chinese) |
 2022, Vol. 48
2022, Vol. 48

