开放科学(资源服务)标志码(OSID):
机械臂作为机器人领域中使用最广的一种机械装置,被应用在各个行业,如从工业生产中的仓库管理、汽车制造,到农业生产中的码垛和瓜果产品的采摘分拣。在工业生产中,许多工厂都是使用示教法对机械臂进行控制的,即事先通过手动拖拽或是使用示教器调整的方式,在移动机械臂到达每一个目标位置时保存各个目标的位置信息,然后使机械臂按照目标点的顺序移动。然而,如果在新的应用中目标位置产生变化,则需要重新示教,因此,这种采用示教的方法不仅耗费人力,灵活性也有所欠缺。除了示教法,应用最为普遍的传统控制方法通过运动规划理论对机械臂进行控制。目前的运动规划理论包括正运动学和逆运动学,正运动学的作用是根据机械臂的各轴转动角度计算得到机械臂末端的位置,而逆运动学则根据机械臂末端的目标位置计算得到各轴所需的转动角度。为了实现更灵活的机械臂应用,越来越多的研究人员开始将人工智能的数据驱动方法应用在机械臂的控制中。本文也将引入数据驱动的深度强化学习算法来解决机械臂的智能控制问题。
强化学习是人工智能的一个分支,其通过与环境的交互得到训练数据,利用数据的训练得到控制模型,进而实现智能决策。当前,为了提升模型的表征能力,研究者将深度神经网络引入到强化学习中,将两者优势互补,提出了可在复杂环境中感知并决策的深度强化学习算法。深度强化学习算法能够在高维度和连续状态空间下有效工作,其研究已经在围棋对弈、Atari游戏等领域取得了较大进展。对于同属连续状态空间的机械臂控制问题,深度强化学习算法也可以很好地加以解决,但存在训练时间消耗巨大的问题。本文提出针对机械臂控制模型先2D后3D的训练方法,在保证应用效果的情况下缩短训练时间。
1 深度强化学习算法 1.1 算法介绍深度强化学习算法作为一种端到端的学习算法,具有很强的通用性,研究者已经利用深度强化学习算法解决了很多智能决策问题:文献[1]提出深度强化学习算法DQN,使智能体学会了玩Atari游戏,并打破了人类保持的记录;文献[2]同样在Atari游戏中使用深度强化学习实现了多智能体之间的对战与合作;文献[3]利用深度强化学习优化了仿人机器人的行走稳定性;文献[4]通过策略搜索的方式完成了飞行器的自主飞行;文献[5]在OpenAI Gym环境下,使用深度强化学习算法完成了对不同结构的双足、四足机器人的仿真训练,并比较了不同算法在训练效果上的差异;文献[6]将深度强化学习加入到目标检测算法中,加快了目标外框的检测速度;文献[7]在超参数的优化中使用强化学习算法,并提出了状态向量、奖励函数和动作的定义方法。
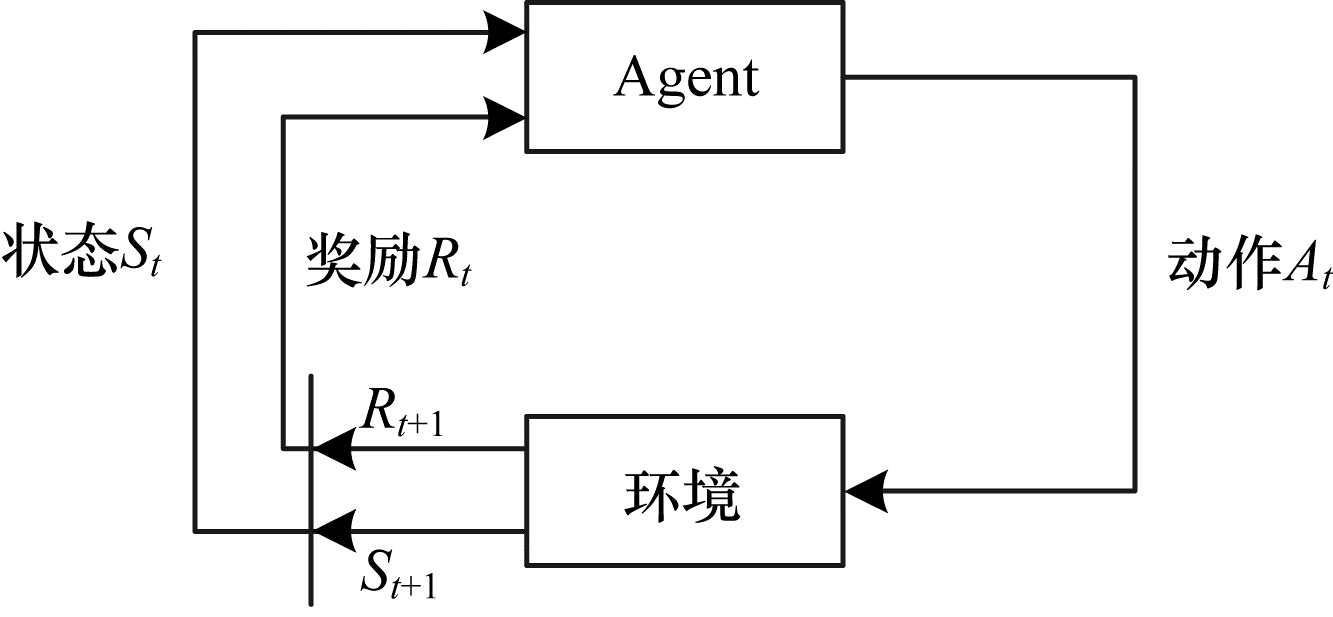
在深度强化学习算法中有以下5大要素:智能体(Agent),环境(Environment),动作(Action),状态(State),奖励(Reward)。如图 1所示,智能体实时地和环境进行交互,智能体观测到状态(状态由状态向量表征,即描述当前状态的物理量个数和取值)后根据策略输出动作(机械臂各个关节电机的旋转角度),而动作会作用于环境进而影响状态。此外,环境还会根据动作和状态给智能体一个奖励(由奖励函数表征,描述是否达到了目标的一个反馈量化值),而智能体则根据动作状态和奖励更新自身选择动作的策略[8]。通过在环境中的不断尝试,获得最大的奖励值,学习到从状态到动作的映射,这种映射就是策略,以参数化的深度神经网络表示。
|
Download:
|
| 图 1 强化学习算法流程 Fig. 1 Procedure of reinforcement learning algorithm | |
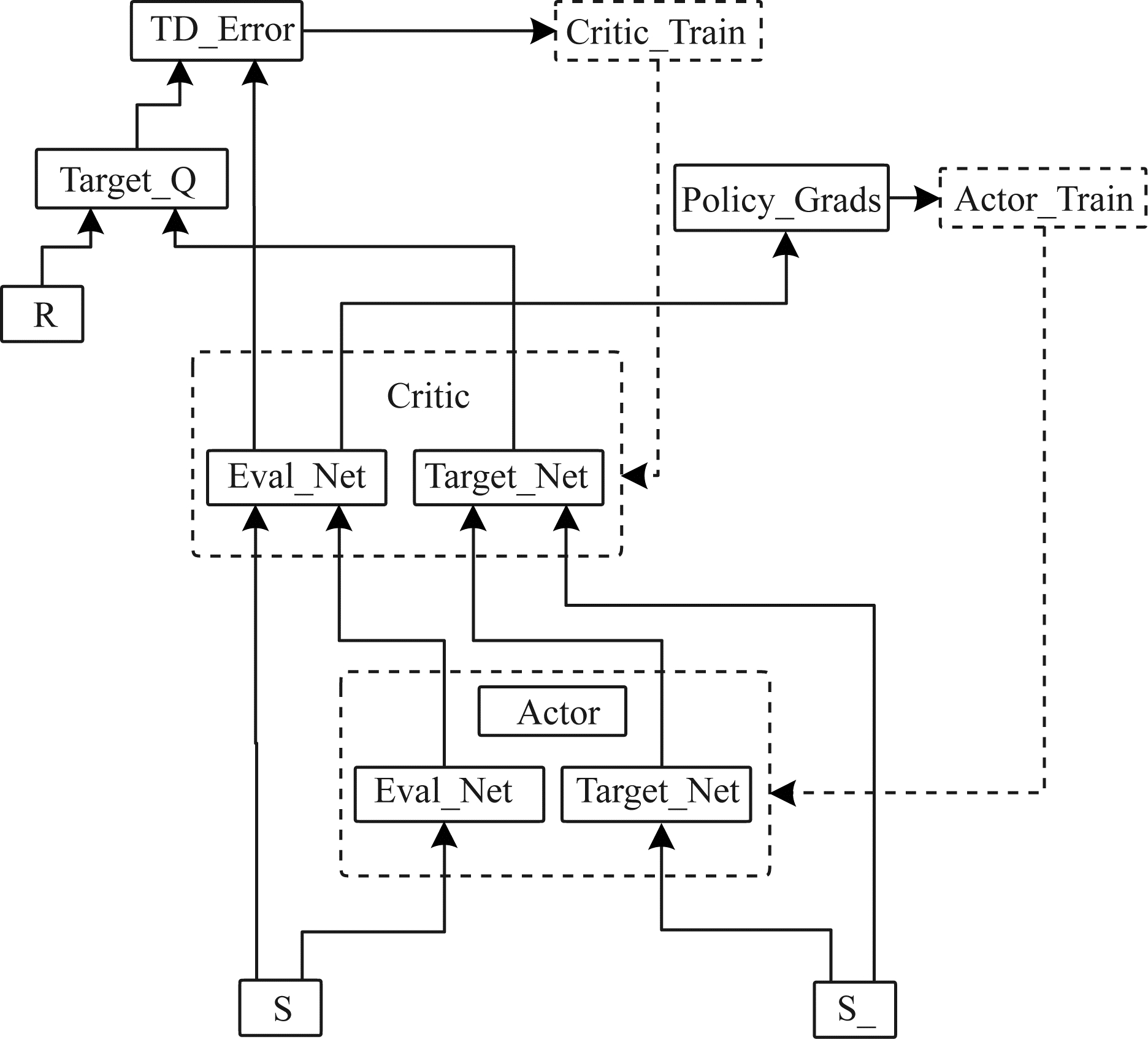
本文中使用的深度强化学习算法是深度确定性策略梯度(Deep Deterministic Policy Gradient,DDPG)算法[9],该算法流程如图 2所示。DDPG算法使用确定性策略梯度(Deterministic Policy Gradient,DPG)算法[10]中的策略网络,采用Actor-Critic框架[11],并结合深度Q网络(Deep Q-Network,DQN)[1]中的经验回放以及目标网络(Target_Net)和评估网络(Eval_Net)分开的技巧,在针对连续动作空间的环境中取得了不错的效果。在DDPG算法架构中包含4个神经网络,分别是Actor的目标网络和评估网络以及Critic的目标网络和评估网络,且2个Actor网络的结构完全相同,2个Critic网络的结构完全相同。
|
Download:
|
| 图 2 DDPG算法流程 Fig. 2 Procedure of DDPG algorithm | |
DDPG算法描述如下:
算法1 DDPG
输入 Actor评估网络,参数为
输出 最优的Actor评估网络参数
1)随机初始化
2)从1到T(训练总回合)进行迭代。
(1)初始化最初状态s。
(2)Actor评估网络基于状态s得到动作
(3)执行动作
(4)将
(5)从经验回放
| $ {y}_{i}=\left\{\begin{array}{l}{r}_{i}, \mathrm{i}\mathrm{s}\_\mathrm{e}\mathrm{n}\mathrm{d}=1\\ {r}_{i}+\gamma {Q}^{\text{'}}({s}_{i}^{\text{'}}, {a}_{i}^{\text{'}}, {\omega }^{\text{'}}), \mathrm{i}\mathrm{s}\_\mathrm{e}\mathrm{n}\mathrm{d}=0\end{array}\right. $ |
(6)使用均方差损失函数
(7)使用
(8)若T%C=1,则通过
(9)若
在深度强化学习中,状态向量、奖励函数是决定算法性能的重要组成部分。一个好的状态向量,能够全面地表征当前所处环境的特征,加快模型训练速度。一个适合的奖励函数,能够准确地表征模型任务目标,加快模型收敛速度。在将深度强化学习算法应用于真实问题时,如何设置状态向量和奖励函数是算法成功的关键,因此,需要使用不同的设置方式进行训练,对两者的收敛性和稳定性进行比较分析,寻找最优的设置方式。
对于状态向量的设置方式,往往根据具体问题的物理量通过经验设置。对于奖励函数的设置方式:文献[12]分析了不同奖励方式对强化学习模型最终效果的影响;文献[13]针对传统Q算法对于机器人奖励函数的定义较为宽泛,导致机器人学习效率不高的问题,提出一种回报详细分类Q(RDC-Q)学习算法,算法的收敛速度相对传统回报Q算法有明显提高。文献[14-16]都是基于内在启发的思路对环境的感知和外部奖励信号进行处理,转化成自己的内在奖励。
1.3 机械臂的算法应用关于针对机械臂的深度强化学习算法训练,已有许多研究者进行了不同的研究和尝试:文献[17]使用DDPG算法以机械臂各个关节角度作为状态向量,针对奖励函数设置问题,提出包含单步奖励、回合稀疏奖励和方向奖励的复合奖励函数,并加入优先经验回放的概念,提升了算法的训练速度;文献[18]在OpenAI Gym的FetchPickAndPlace-v1环境中,专门针对机械臂控制进行了奖励函数的设计,通过不同奖励函数训练,得到了机械臂通过不同的轨迹到达目标位置的策略;文献[19]采用人工免疫原理对RBF网络训练数据集的泛化能力在线调整隐层结构,生成RBF网络隐层,当网络结构确定时,采用递推最小二乘法确定网络连接权值,由此对神经网络的网络结构和连接权进行自适应调整和学习,大幅提高了机械臂逆运动学求解精度。文献[20]提出了基于增广示教的机械臂轨迹规划方法,在经验回放中提前加入少量的示教信息,有效地降低了训练初期的难度,获得了更优秀的性能,并在Gazebo仿真平台下的Kent6 V2机械臂上得到了验证。在训练耗时方面:文献[21]在Unity中搭建了包括机械臂和目标物品的3D模型,直接在3D模型中通过DDPG算法控制机械臂到达目标下方,并将其托举起,整个训练过程平均消耗33 h,相较于传统调试方法效率提升近61%。
本文提出先简化模型(2D模型)再复杂模型(3D模型)的训练方法,使寻找合理的状态向量设置和奖励函数形式的训练时长大幅缩短,由此构建能控制3D机械臂到达目标位置的深度强化学习算法模型,提升算法效率。
2 模型训练本文通过深度强化学习算法进行训练得到机械臂的控制模型(一个深度神经网络),其动作是机械臂各转动轴的转动角度,而对于状态向量和奖励函数形式的选取,则根据经验使用不同的设置方式进行训练。
深度强化学习算法的训练过程是异常耗时的,通过对训练模型采取不同的状态向量和奖励函数形式来寻找合理的设置方式,会使得训练时长成倍增长。为缩减训练时间,本文先在不具备物理属性的2D机械臂仿真模型上进行训练,这一过程主要目的是找到合理的状态向量和奖励函数设置方式,然后基于此设置方式,迁移到具备物理属性的3D仿真环境中进行训练,3D仿真环境中的机械臂和现实世界的真实机械臂在物理属性上已经非常接近。本文采用的真实机械臂是越疆科技的Dobot Magician,其在3D仿真环境Gazebo中的模型与真是机械臂物理属性一致。
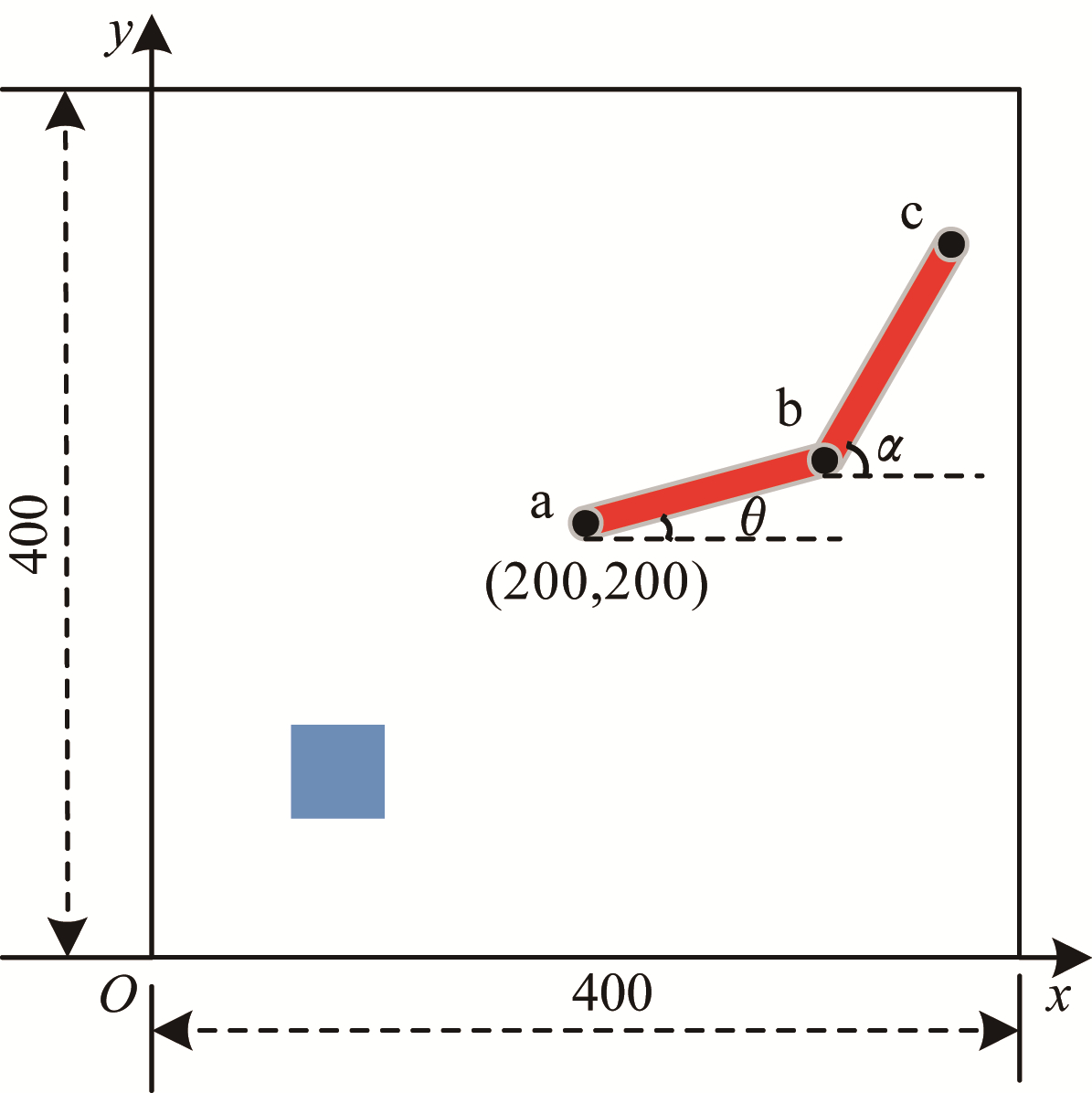
2.1 2D机械臂训练仿真分析本文所使用的2D机械臂仿真效果如图 3所示[22](彩色效果见《计算机工程》官网HTML版)。该2D机械臂环境以图中左下角为坐标原点,长宽均为400;图中蓝色方块为目标区域,中心点坐标为(100,100),长宽均为40;两连杆为一个二轴机械臂,a点为固定关节,在整个环境的正中心,坐标为(200,200),b点和c点均为自由关节,c点为机械臂末端,连杆ab和连杆bc的长度均为200,用
|
Download:
|
| 图 3 2D机械臂仿真效果示意图 Fig. 3 Schematic diagram of 2D manipulator simulation effect | |
一个好的状态向量能够完整地展示整个学习的环境特征,这样深度强化学习模型就能够依据这些状态从中学到有价值的策略。好的状态向量在加速模型的收敛速度以及提高模型稳定性上起到了至关重要的作用。
经过分析,最终得到如表 1所示的6种针对2D机械臂的状态向量设置方法,其中各个参数的具体含义见表 2。

|
下载CSV 表 1 2D机械臂状态向量设置方式 Table 1 2D manipulator status vector setting patterns |

|
下载CSV 表 2 2D机械臂状态向量中各参数含义 Table 2 Definition of each parameter in 2D manipulator state vector |
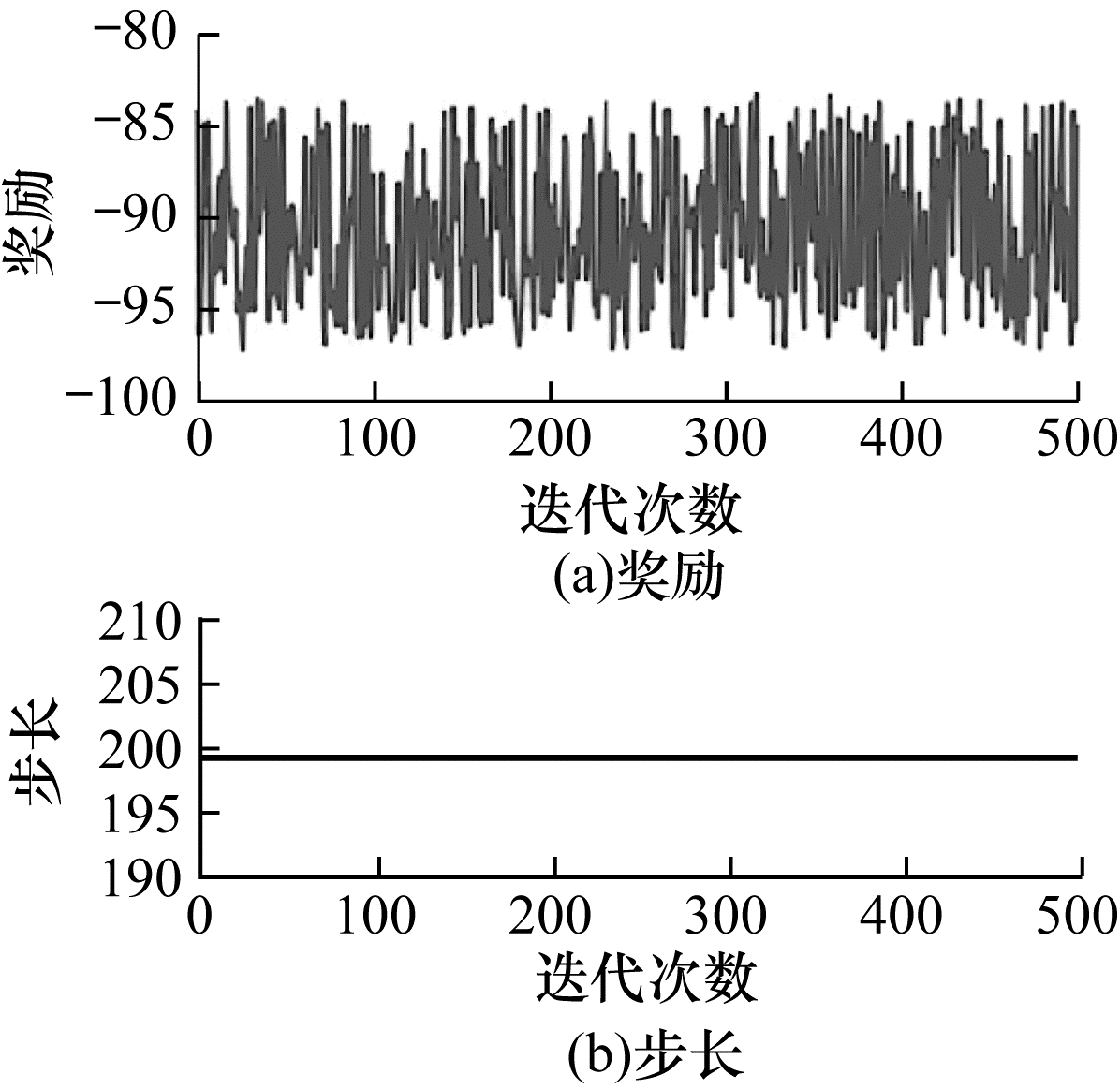
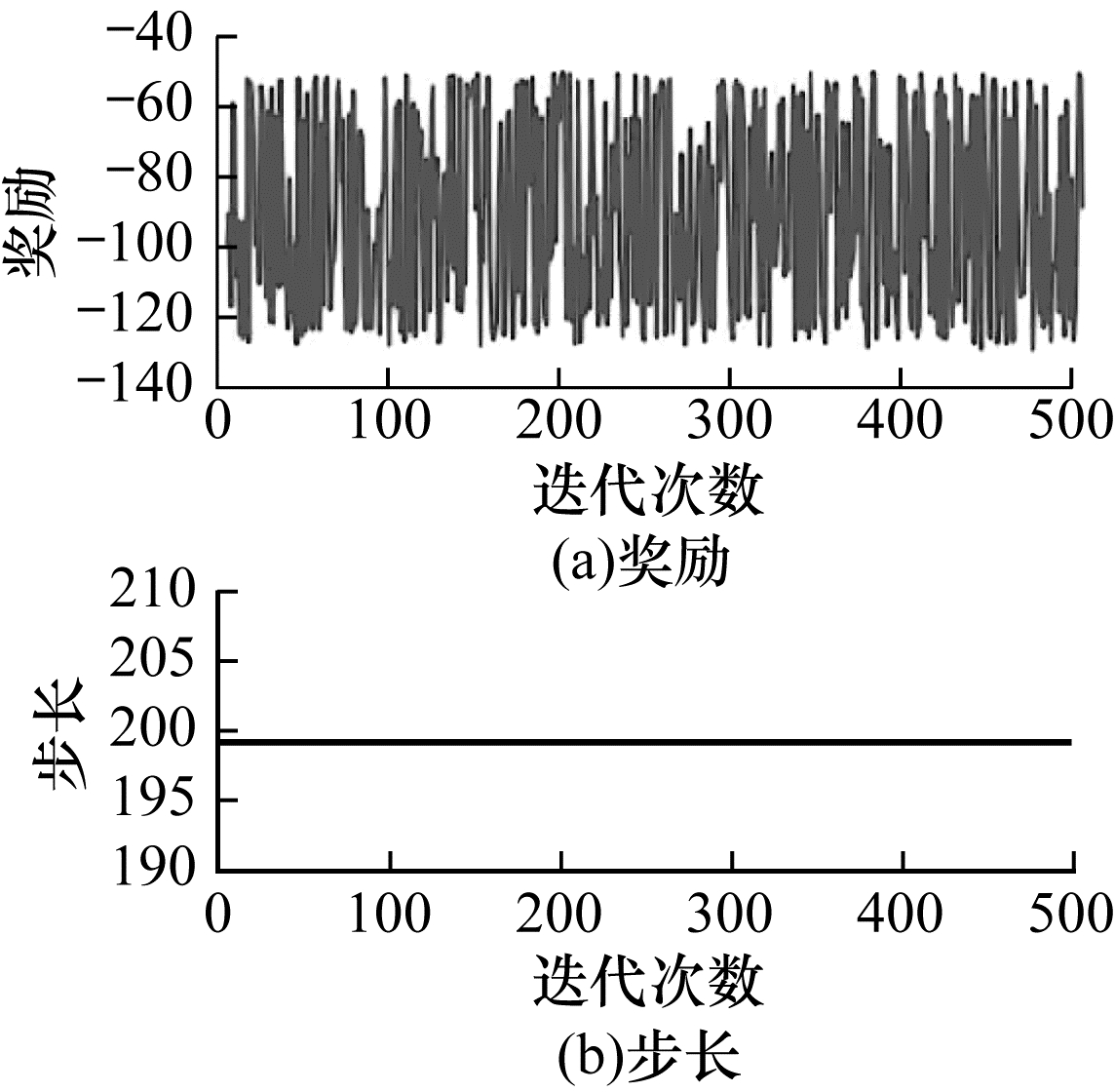
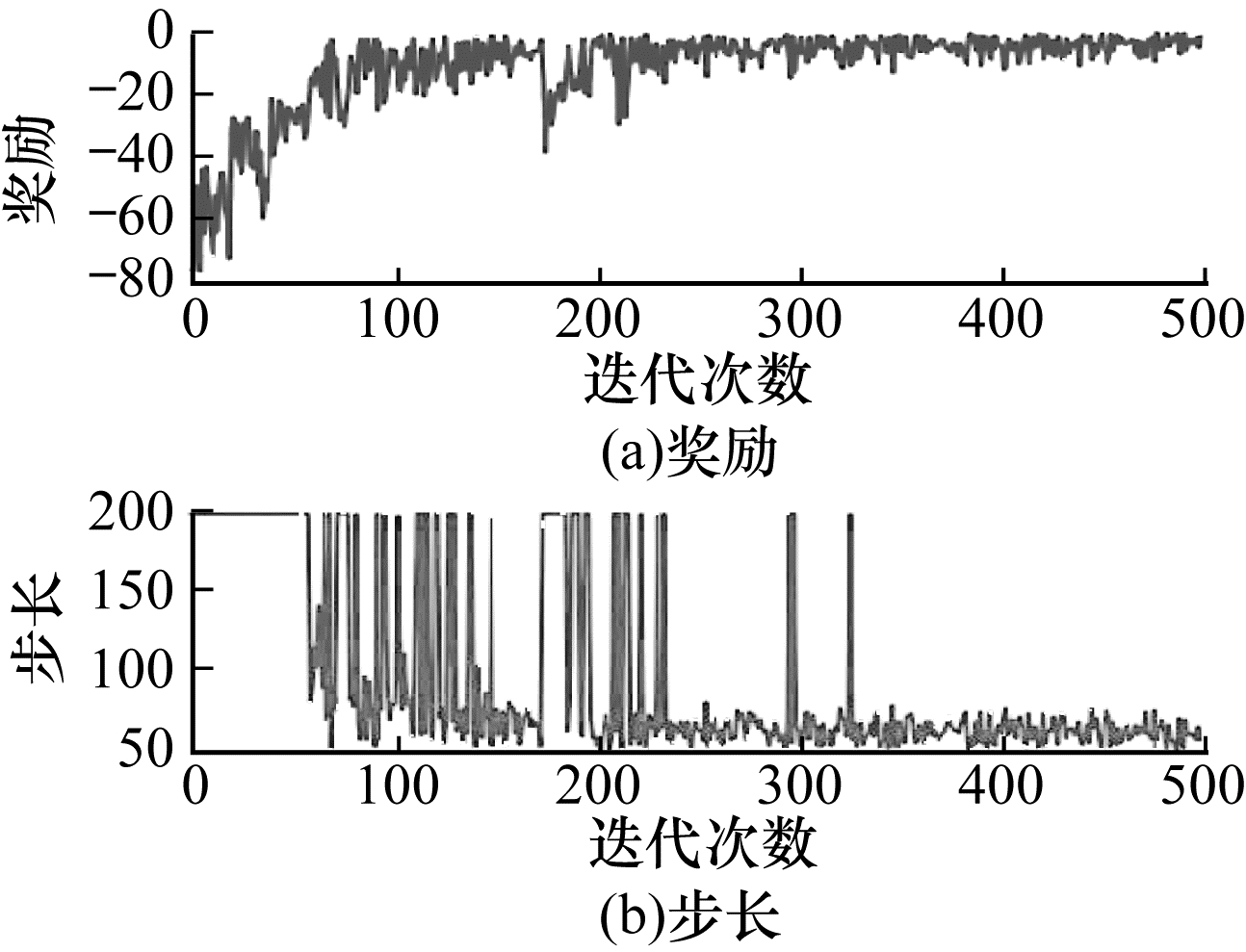
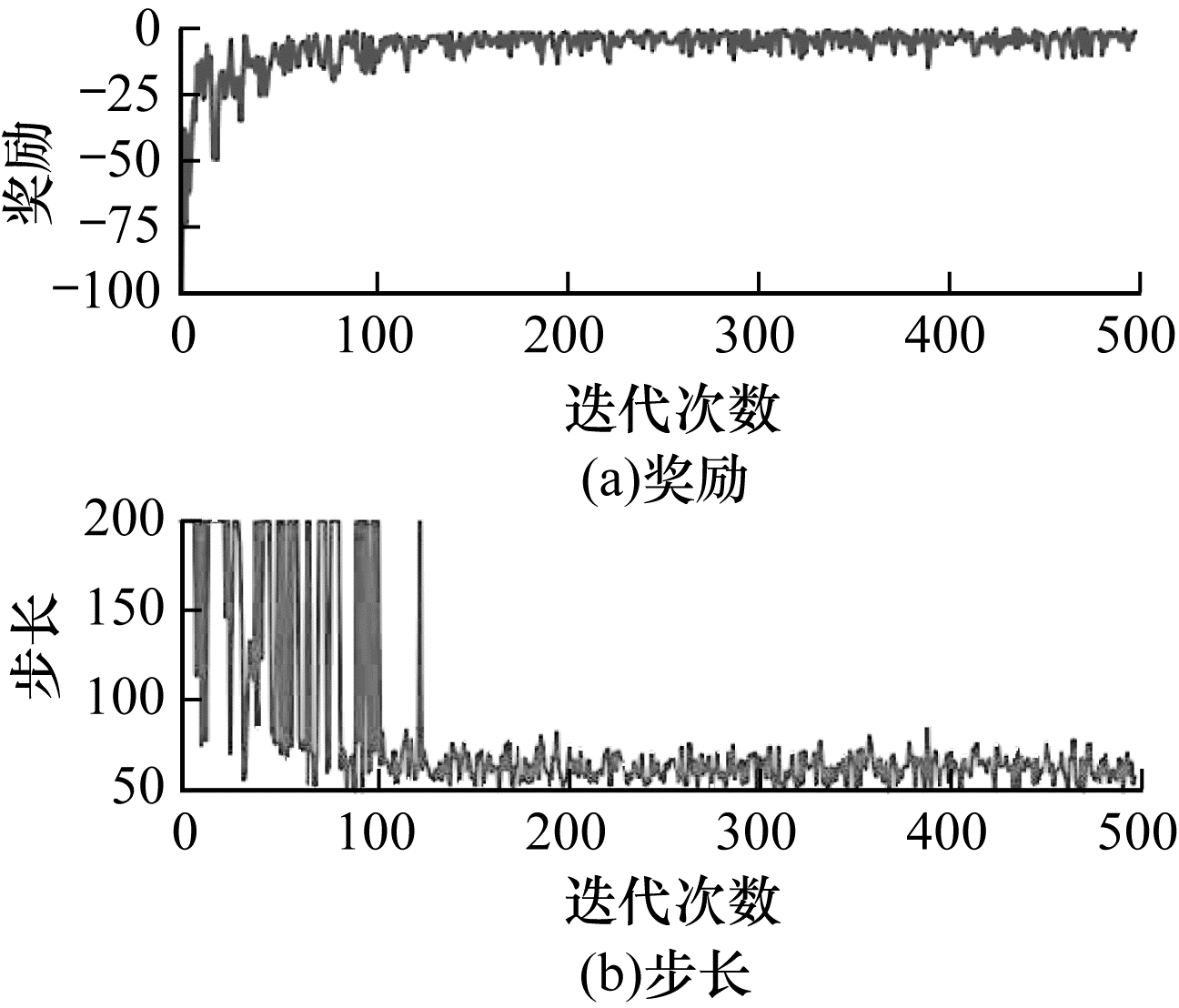
本文将以上状态设置方法应用在深度强化学习算法中,进行500回合每回合最大200步的训练,得到结果如图 4~图 9所示。可以看出:使用标准化后的末端和中端坐标以及末端和中端与目标之间的直线距离和x、y两轴距离作为状态的效果最好,收敛速度快,且收敛后稳定其原因如下:
|
Download:
|
| 图 4 使用2D机械臂状态向量设置方式1的训练结果 Fig. 4 Training results while using 2D manipulator status vector setting pattern 1 | |
|
Download:
|
| 图 5 使用2D机械臂状态向量设置方式2的训练结果 Fig. 5 Training results while using 2D manipulator status vector setting pattern 2 | |

|
Download:
|
| 图 6 使用2D机械臂状态向量设置方式3的训练结果 Fig. 6 Training results while using 2D manipulator status vector setting pattern 3 | |
|
Download:
|
| 图 7 使用2D机械臂状态向量设置方式4的训练结果 Fig. 7 Training results while using 2D manipulator status vector setting pattern 4 | |

|
Download:
|
| 图 8 使用2D机械臂状态向量设置方式5的训练结果 Fig. 8 Training results while using 2D manipulator status vector setting pattern 5 | |
|
Download:
|
| 图 9 使用2D机械臂状态向量设置方式6的训练结果 Fig. 9 Training results while using 2D manipulator status vector setting pattern 6 | |
1)状态向量中不仅包含了末端坐标,而且还包含了末端与目标的位置关系和中端与目标的位置关系,这样的状态向量能够更详细地描述机械臂整体与目标之间相对位置信息,也使算法模型能够更全面地了解和学习环境。
2)使用标准化或归一化对神经网络训练的输入量进行预处理能够消除奇异样本对训练的影响,加快网络模型的收敛速度。
综合考虑以上因素,本文最终选择表 1中第6种设置方式作为针对2D机械臂的最优状态向量。
2.1.2 奖励函数设置在强化学习领域,奖励函数的设计对于算法收敛速度和稳定性方面也起到关键作用。一个好的奖励函数能够清晰地告诉强化学习算法任务目标是什么,强化学习算法就能够依据奖励函数快速学习。
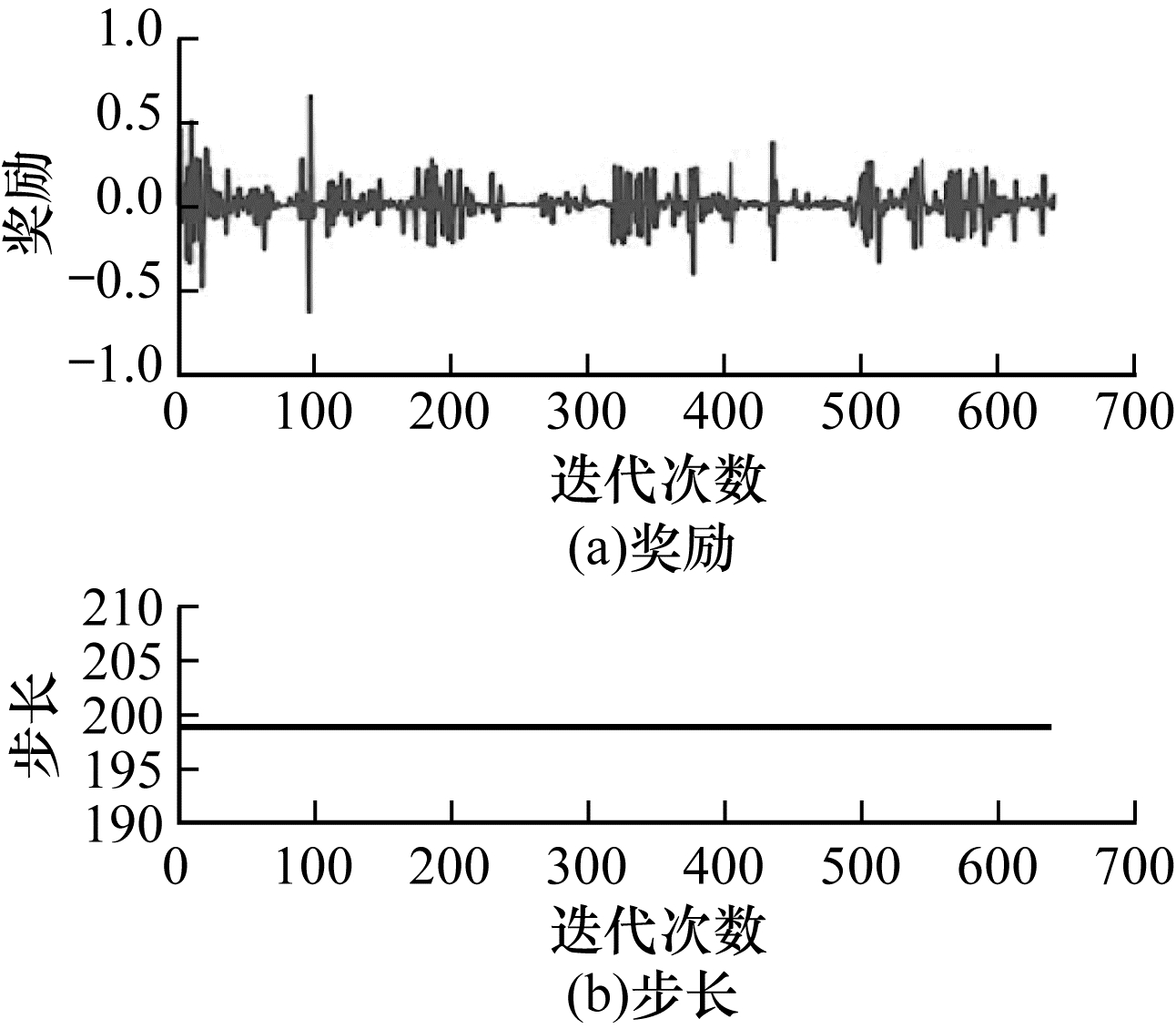
本文分别选用如表 3中的4种奖励函数设置方式,各参数的具体含义见表 4。选用以上4种奖励函数设置方式进行500回合每回合最大200步的训练,得到结果如图 10~图 13所示。

|
下载CSV 表 3 2维机械臂奖励函数设置方式 Table 3 2D manipulator reward function setting patterns |

|
下载CSV 表 4 2维机械臂奖励函数中各参数含义 Table 4 Definition of each parameter in 2D manipulator reward function |
|
Download:
|
| 图 10 使用2维机械臂奖励函数设置方式1的训练结果 Fig. 10 Training results while using 2D manipulator reward function setting pattern 1 | |
|
Download:
|
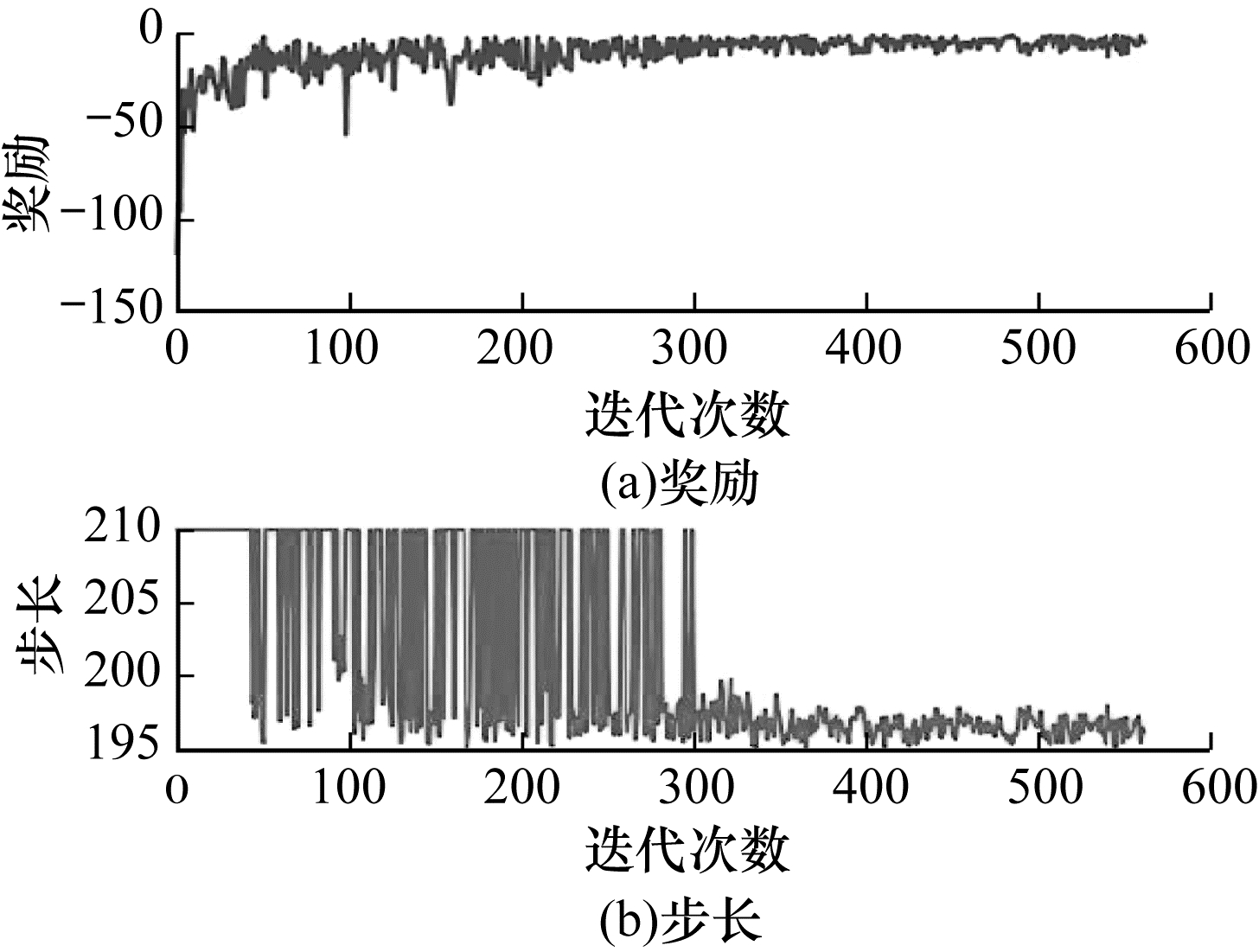
| 图 11 使用2维机械臂奖励函数设置方式2的训练结果 Fig. 11 Training results while using 2D manipulator reward function setting pattern 2 | |
|
Download:
|
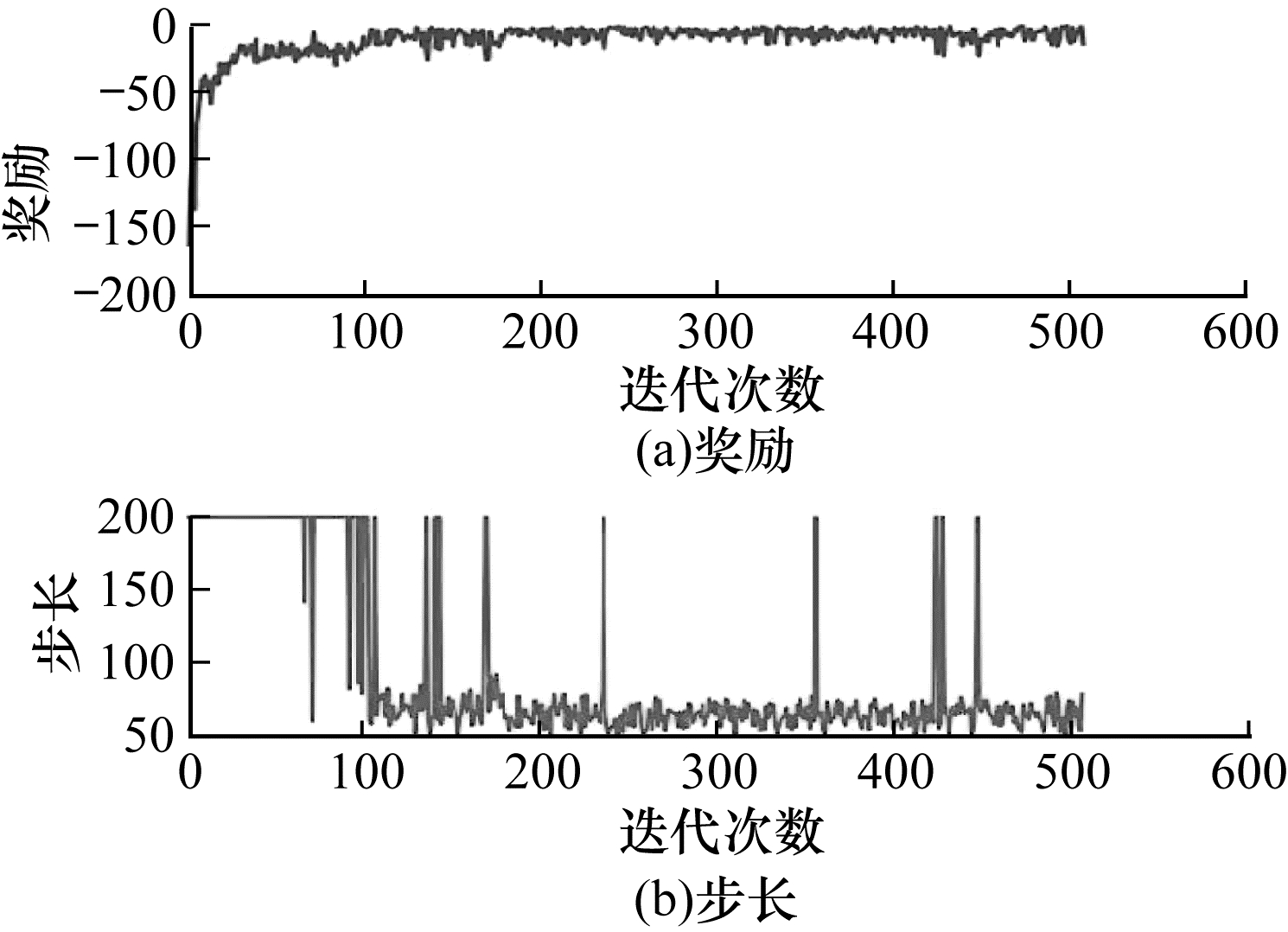
| 图 12 使用2维机械臂奖励函数设置方式3的训练结果 Fig. 12 Training results while using 2D manipulator reward function setting pattern 3 | |
|
Download:
|
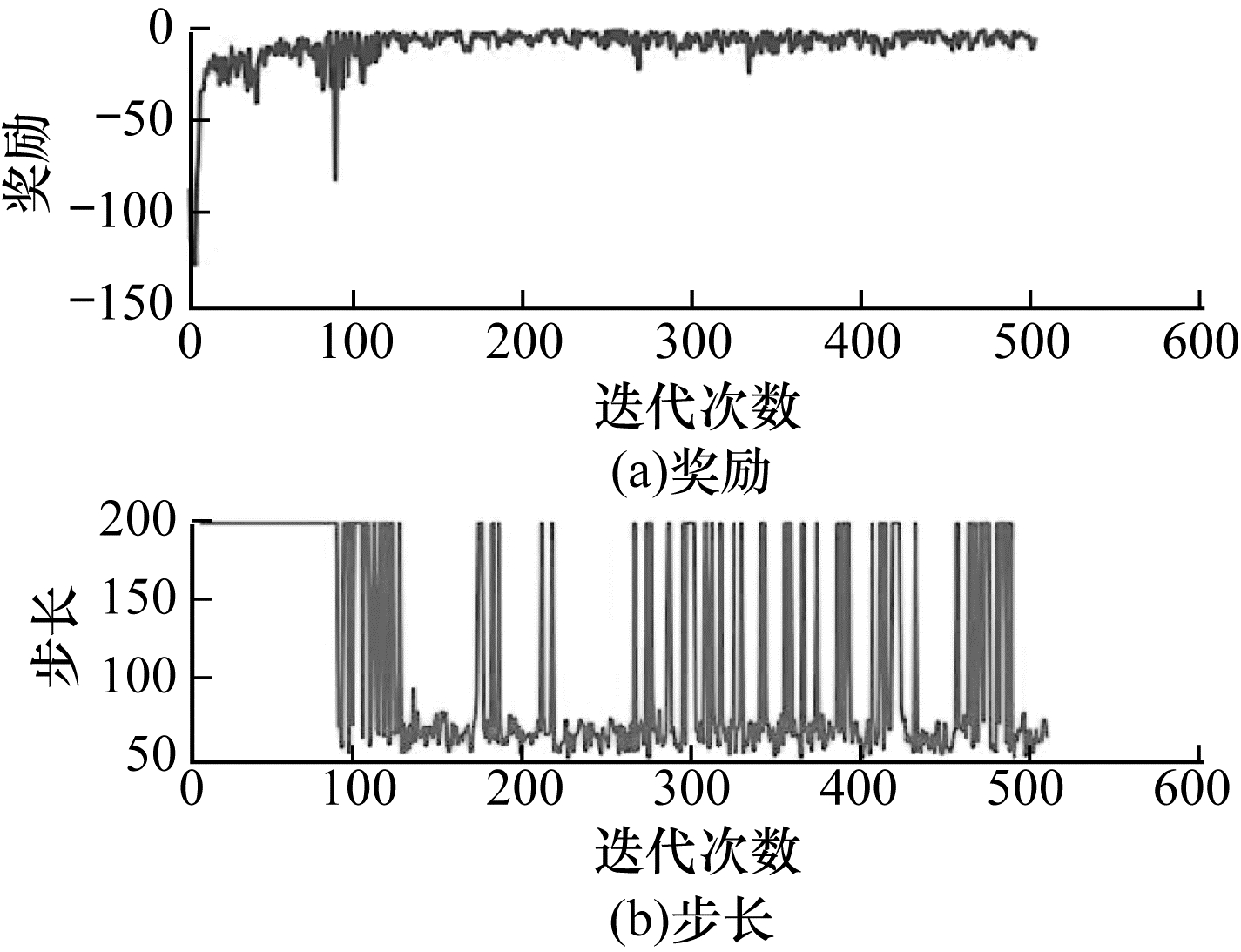
| 图 13 使用2维机械臂奖励函数设置方式4的训练结果 Fig. 13 Training results while using 2D manipulator reward function setting pattern 4 | |
可以看出:使用执行动作前后距离差作为奖励并没有使强化学习算法很好地了解到任务目的,每回合步数和每回合奖励均未收敛;当单纯地使用末端与目标之间直线距离的负值时,收敛后的稳定性最好;而使用末端与目标之间x、y两轴距离和的负值作为奖励时,收敛速度最快,但是收敛后的稳定性不足;在使用负的距离奖励加上到达目标奖励时,虽然每回合奖励的收敛速度快,但是在收敛后会出现“甩手”的现象(每回合步数大,但是奖励值小,机械臂末端在目标区域边缘晃动)。最终,本文选择使用结果最为稳定的末端与目标之间直线距离的负值作为针对2D机械臂的最优奖励函数。
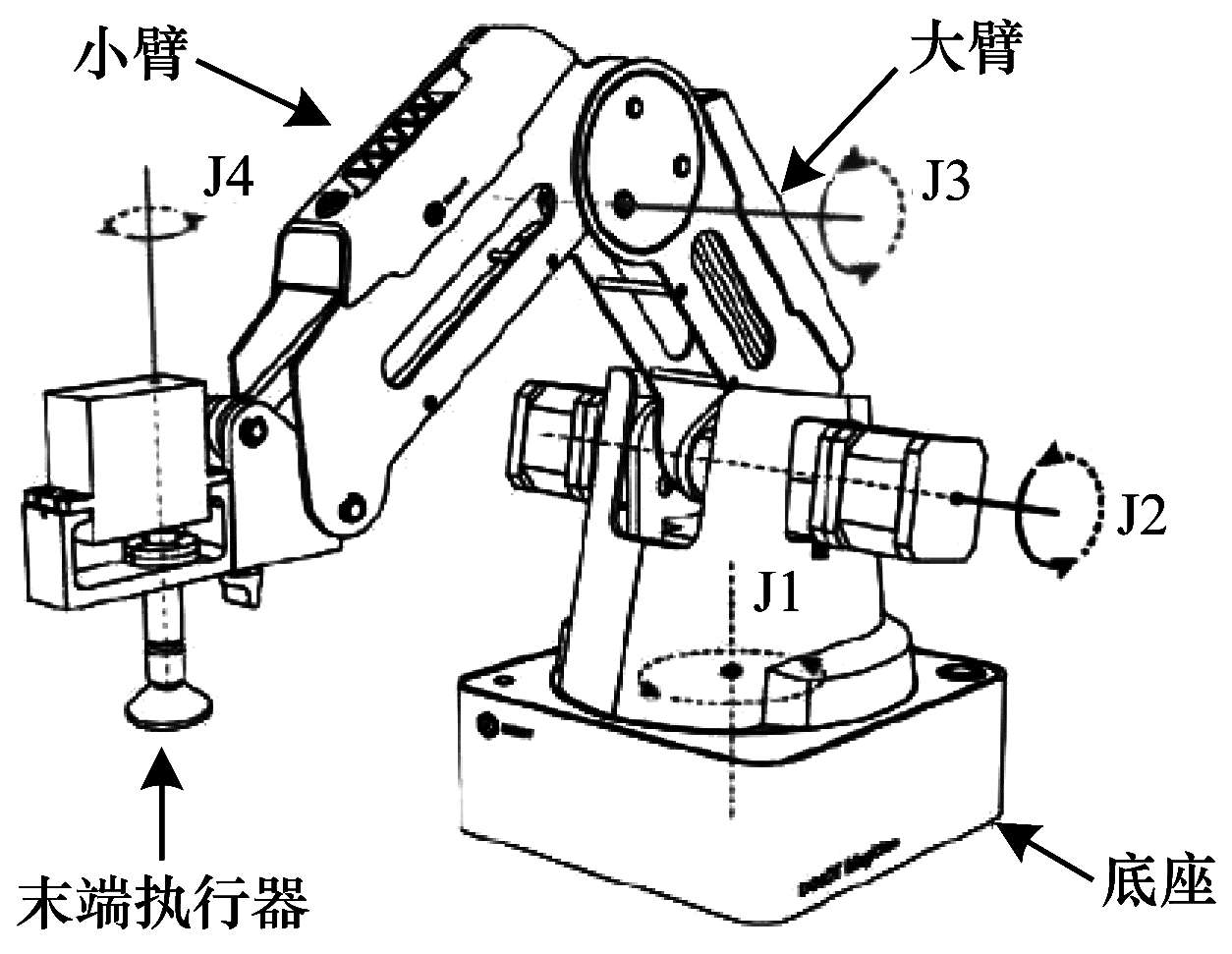
2.2 3D机械臂训练仿真分析Dobot Magician机械臂结构如图 14所示,由图中可知,该机械臂主要由底座、大臂、小臂和末端执行器4个部分组成,连接处有4个旋转关节Joint1~Joint4,其中,Joint1~Joint3用于控制末端位置,而Joint4则用于控制末端执行器的角度。图 15为在Gazebo仿真环境下的3D机械臂,是通过越疆公司给出的Urdf模型导出的,其中并没有包含末端执行器,其余机械结构和实物一致。图 16为实物机械臂的图片。
|
Download:
|
| 图 14 Dobot Magician结构 Fig. 14 Structure of Dobot Magician | |

|
Download:
|
| 图 15 Gazebo中的Dobot Magician模型 Fig. 15 Dobot Magician model in Gazebo | |

|
Download:
|
| 图 16 实物Dobot Magician机械臂 Fig. 16 Real Dobot Magician | |
根据2.1节中仿真训练确定的2D机械臂环境下的最优状态向量和奖励函数,本文将其迁移到3D环境中,加入了z轴的信息,并对3D机械臂进行标定,使用机械臂的第三轴Joint3作为中端mid,末端执行器作为末端end,得到状态向量如下:
| $ \begin{array}{l} s = [{x_{{\rm{end}}}},{y_{{\rm{end}}}},{z_{{\rm{end}}}},{d_{{\rm{end\_to\_obj}}}},{d_{{\rm{end\_to\_obj\_x}}}},{d_{{\rm{end\_to\_obj\_y}}}},\\ \;\;\;\;\;\;{d_{{\rm{end\_to\_obj\_z}}}},{x_{{\rm{mid}}}},{y_{{\rm{mid}}}},{z_{{\rm{mid}}}},{d_{{\rm{mid\_to\_obj}}}},{d_{{\rm{mid\_to\_obj\_x}}}},\\ \;\;\;\;\;\;{d_{{\rm{mid\_to\_obj\_y}}}},{d_{{\rm{mid\_to\_obj\_z}}}},{i_{{\rm{indicator}}}}] \end{array}$ | (1) |
| $ s = (s - {s_{{\rm{mean}}}})/{s_{{\rm{std}}}} $ | (2) |
使用末端与目标之间的距离的负值作为奖励:
| $ r = - {d_{{\rm{end\_to\_obj}}}} $ | (3) |
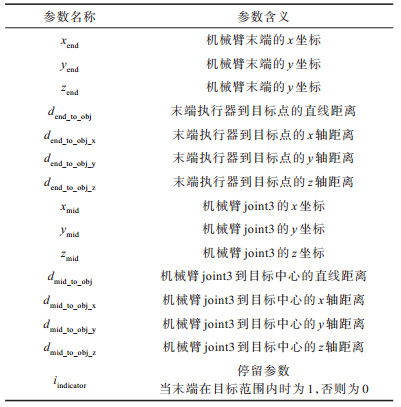
各参数的具体含义见表 5。
|
下载CSV 表 5 3维机械臂各参数含义 Table 5 Definition of each parameter in 3D manipulator |
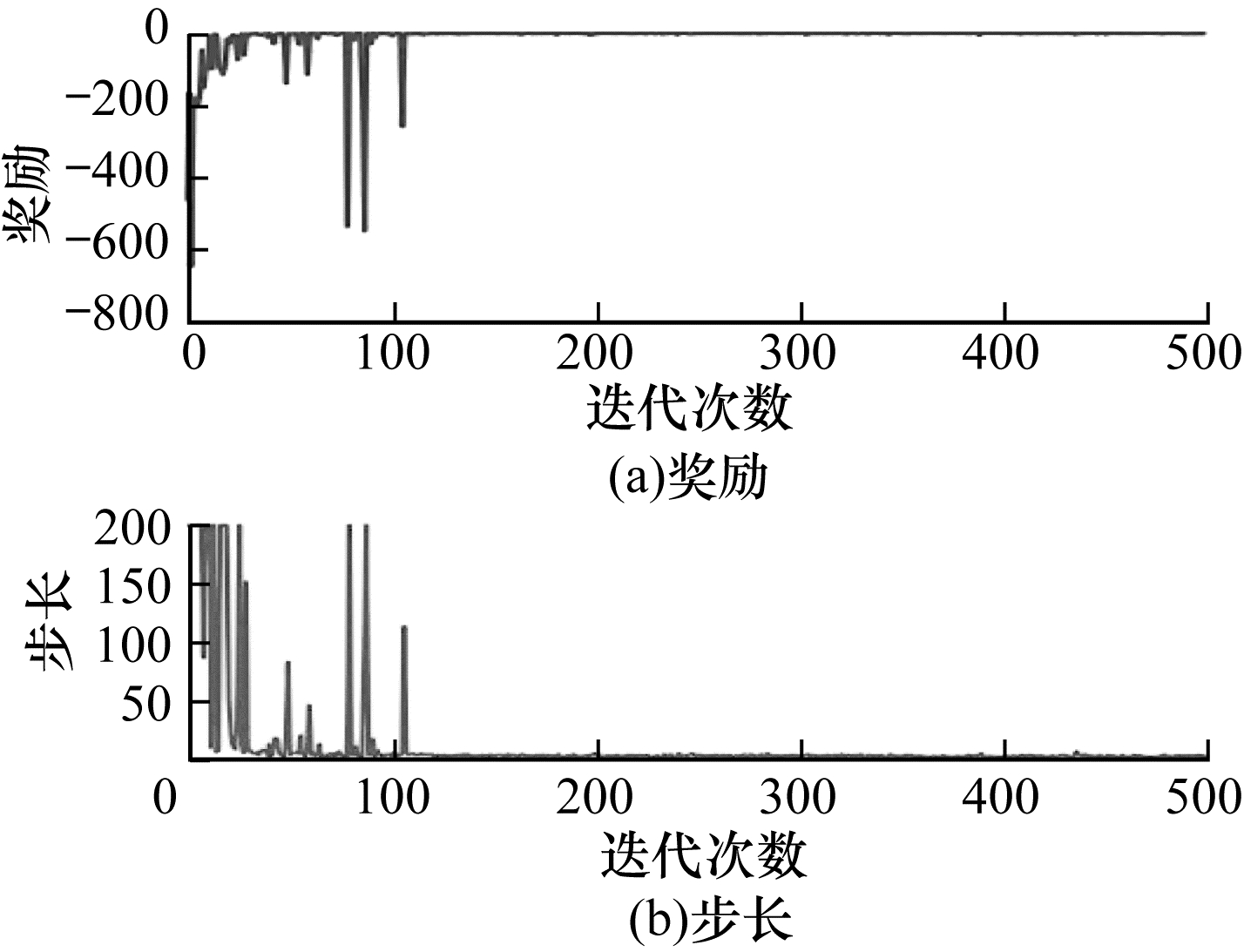
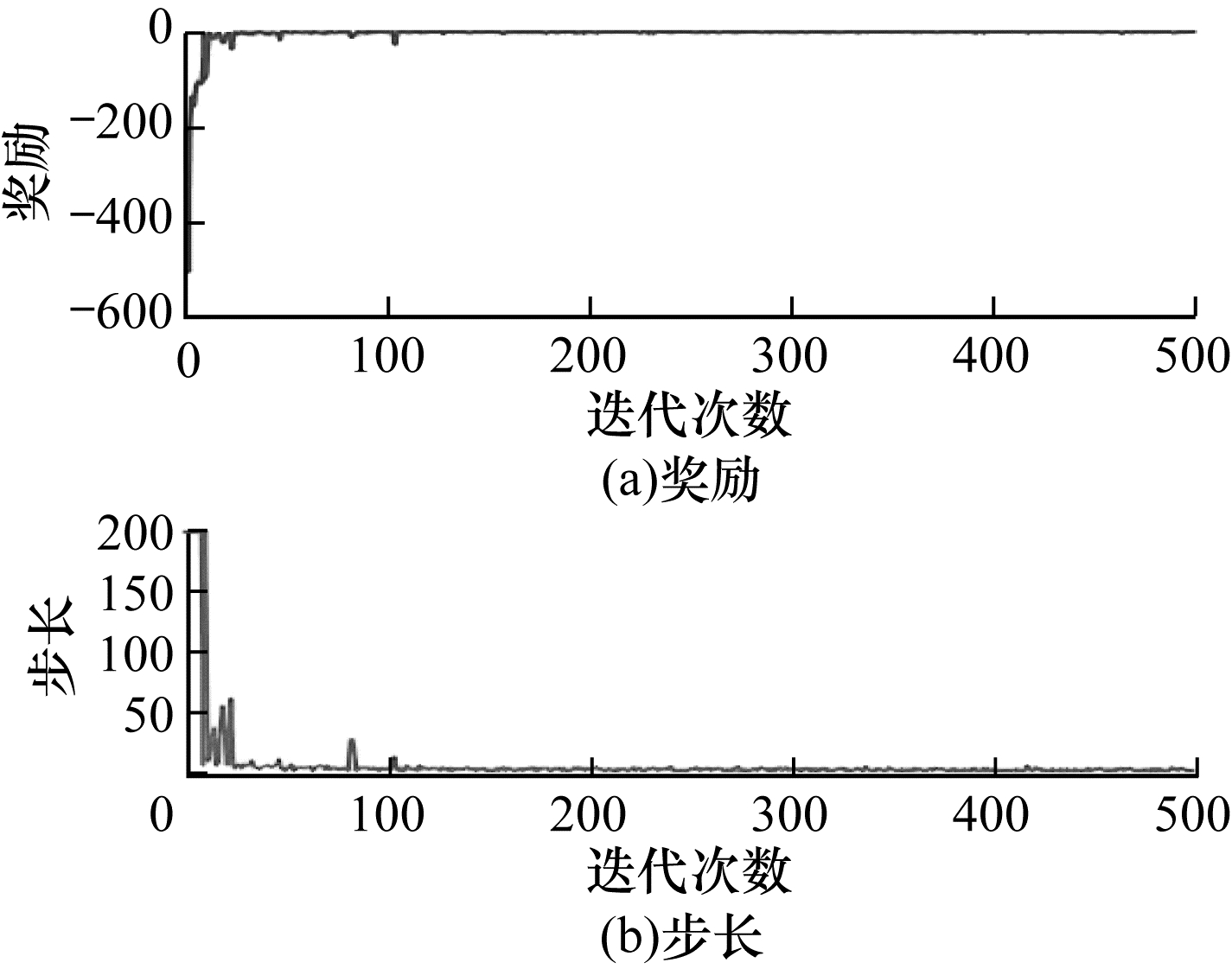
在对奖励函数和状态向量设置完成后,使用固定的目标位置,在Gazebo仿真环境下进行训练,每次500回合,每回合最大200步,最终得到的训练结果如图 17~图 18所示。可以看出:本文使用的奖励函数和状态向量设置在3D机械臂环境下,针对固定目标位置的训练效果好,收敛速度快,且收敛后稳定,并没有出现“甩手”的情况。
|
Download:
|
| 图 17 固定目标位置的训练结果1 Fig. 17 Training result 1 for fixed target positions | |
|
Download:
|
| 图 18 固定目标位置的训练结果2 Fig. 18 Training result 2 for fixtarget positions | |
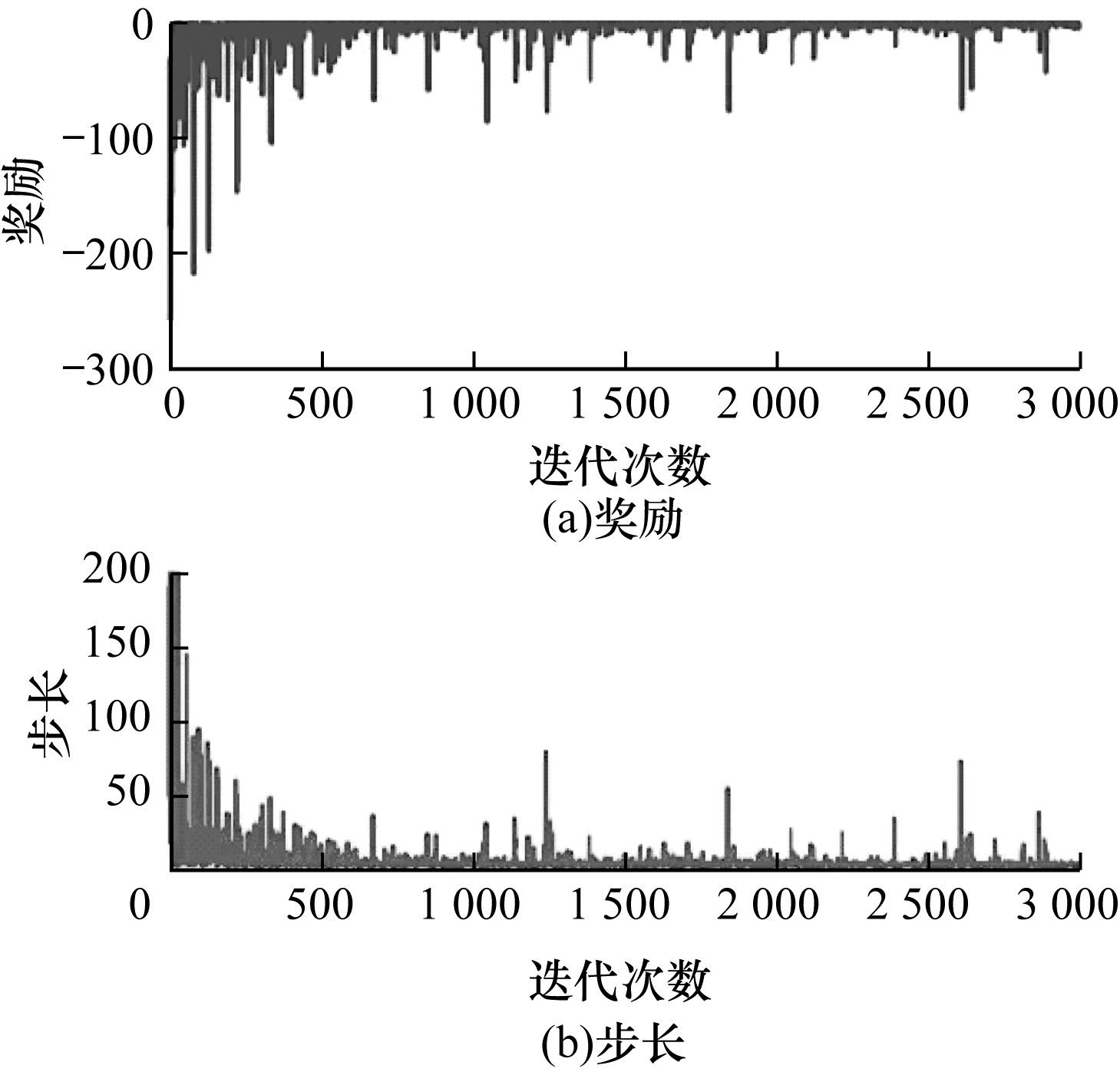
在完成对固定目标位置的训练后,为了能够在真实场景下应用,对目标位置在每回合开始前进行随机的初始化,使用相同的奖励函数和状态向量设置进行训练,每次3 000回合,每回合最大200步,最终得到的训练结果如图 19~图 20所示。可以看出:每回合的总步数和总奖励在1 000回合左右收敛,且收敛后的稳定性良好。

|
Download:
|
| 图 19 随机目标位置的训练结果1 Fig. 19 Training result 1 for random target positions | |
|
Download:
|
| 图 20 随机目标位置的训练结果2 Fig. 20 Training result 2 for random target positions | |
以上结果充分说明了本文所使用的奖励函数和状态向量能够很好地描述机械臂所处的环境与任务目标,同时加快强化学习模型的收敛速度,提高收敛后的稳定性。
本文采用2D机械臂仿真完成状态向量和奖励函数的设置方式选择,并成功迁移到3D机械臂的训练上。在总耗时方面,包括2D机械臂仿真中状态向量和奖励函数的探索以及3D机械臂针对随机目标的训练,平均共消耗约16 h。与文献[21]中直接在3D机械臂上训练方式相比,训练时间提升了近52%。最终,训练得到的控制模型部署在真实机械臂上,其控制效果达到了应用要求,具体可见https://www.bilibili.com/video/BV12v41117jQ视频。
3 结束语在机器人应用领域,一个可以快速控制机械臂到达目标位置完成抓取和摆放的机械臂控制器,能够在很大程度上提高生产效率。本文使用基于数据驱动的深度强化学习算法DDPG代替传统运动学求解方法,针对2D机械臂进行训练仿真找到合理的状态向量和奖励函数设置方式,并将其迁移到3D机械臂的仿真环境中进行训练,最终得到能够快速控制真实机械臂的控制模型。在训练中考虑到强化学习算法训练时间冗长,本文提出先2D后3D的训练方式,训练时间相较于直接3D训练缩短近52%。后续将构建存在障碍物的机械臂操作环境,通过深度强化学习算法训练得到控制模型,进一步提升机械臂操控的智能化水平。
| [1] |
MNIH V, KAVUKCUOGLU K, SILVER D, et al. Playing Atari with deep reinforcement learning[EB/OL]. [2021-06-10]. https://arxiv.org/abs/1312.5602.
|
| [2] |
TAMPUU A, MATIISEN T, KODELJA D, et al. Multiagent cooperation and competition with deep reinforcement learning[J]. PLoS One, 2017, 12(4): 1-10. |
| [3] |
陈奇石. 强化学习在仿人机器人行走稳定控制上的研究及实现[D]. 广州: 华南理工大学, 2016. CHEN Q S. Study and implement of reinforcement learning in biped robot balance control[D]. Guangzhou: South China University of Technology, 2016. (in Chinese) |
| [4] |
ZHANG T H, KAHN G, LEVINE S, et al. Learning deep control policies for autonomous aerial vehicles with MPC-guided policy search[C]//Proceedings of IEEE International Conference on Robotics and Automation. Washington D.C., USA: IEEE Press, 2016: 528-535.
|
| [5] |
DUAN Y, CHEN X, HOUTHOOFT R, et al. Benchmarking deep reinforcement learning for continuous control[C]//Proceedings of the 33rd International Conference on Machine Learning. New York, USA: ACM Press, 2016: 1329-1338.
|
| [6] |
CAICEDO J C, LAZEBNIK S. Active object localization with deep reinforcement learning[C]//Proceedings of IEEE International Conference on Computer Vision. Washington D.C., USA: IEEE Press, 2015: 2488-2496.
|
| [7] |
HANSEN S. Using deep Q-learning to control optimization hyperparameters[EB/OL]. [2021-06-10]. https://arxiv.org/abs/1602.04062.
|
| [8] |
RICHARD S, SUTTON, BARTO A G. Reinforcement learning: an introduction[M]. Cambridge, USA: MIT Press, 1998.
|
| [9] |
DEGRIS T, WHITE M, SUTTON R S. Off-policy actor-critic[EB/OL]. [2021-06-10]. https://arxiv.org/pdf/1205.4839.pdf.
|
| [10] |
ZHANG A, CASARI A. Feature engineering for machine learning[M]. [S. l. ]: O'Reilly Media, 2018.
|
| [11] |
SCOTT S, MATWIN S. Feature engineering for text classification[C]//Proceedings of the 16th International Conference on Machine Learning. Berlin, Germany: 1999: 379-388.
|
| [12] |
DEWEY D. Reinforcement learning and the reward engineering principle[C]//Proceedings of 2014 AAAI Spring Symposium. Palo Alto, USA: AAAI Press, 2014: 1-10.
|
| [13] |
王子强, 武继刚. 基于RDC-Q学习算法的移动机器人路径规划[J]. 计算机工程, 2014, 40(6): 211-214. WANG Z Q, WU J G. Mobile robot path planning based on RDC-Q learning algorithm[J]. Computer Engineering, 2014, 40(6): 211-214. (in Chinese) |
| [14] |
SINGH S, BARTO A G, CHENTANEZ N. Intrinsically motivated reinforcement learning[EB/OL]. [2021-06-10]. https://www.researchgate.net/profile/Satinder-Singh-3/publication/221619598_Intrinsically_Motivated_Reinforcement_Learning/links/55ad05af08aee079921caa19/Intrinsically-Motivated-Reinforcement-Learning.pdf.
|
| [15] |
SORG J, SINGH S, LEWIS R, et al. Internal rewards mitigate agent boundedness[C]//Proceedings of the 27th International Conference on Machine Learning. New York, USA: ACM Press, 2010: 1007-1014.
|
| [16] |
SORG J, SINGH S, LEWIS R. Reward design via online gradient ascent[C]//Proceedings of the 23rd International Conference on Neural Information Processing Systems. New York, USA: ACM Press, 2010: 2190-2198.
|
| [17] |
卜令正. 基于深度强化学习的机械臂控制研究[D]. 徐州: 中国矿业大学, 2019. BU L Z. Study of robot arm control based on deep reinforcement learning[D]. Xuzhou: China University of Mining and Technology, 2019. (in Chinese) |
| [18] |
NAGPAL R, KRISHNAN A U, YU H S. Reward engineering for object pick and place training[EB/OL]. [2020-06-10]. https://arxiv.org/abs/2001.03792.
|
| [19] |
魏娟, 杨恢先, 谢海霞. 基于免疫RBF神经网络的逆运动学求解[J]. 计算机工程, 2010, 36(22): 192-194. WEI J, YANG H X, XIE H X. Solution of inverse kinematics based on immune RBF neural network[J]. Computer Engineering, 2010, 36(22): 192-194. (in Chinese) |
| [20] |
郑钧天. 基于深度强化学习的机械臂轨迹规划仿真[D]. 成都: 电子科技大学, 2020. ZHENG J T. Simulation for manipulator trajectory planning based on deep reinforcement learning[D]. Chengdu: University of Electronic Science and Technology of China, 2020. (in Chinese) |
| [21] |
李鹤宇, 赵志龙, 顾蕾, 等. 基于深度强化学习的机械臂控制方法[J]. 系统仿真学报, 2019, 31(11): 2452-2457. LI H Y, ZHAO Z L, GU L, et al. Robot arm control method based on deep reinforcement learning[J]. Journal of System Simulation, 2019, 31(11): 2452-2457. (in Chinese) |
 2022, Vol. 48
2022, Vol. 48

