2. 贵州财经大学 信息学院, 贵阳 550025;
3. 贵州大学 数学与统计学院, 贵阳 550025
2. School of Information, Guizhou University of Finance and Economics, Guiyang 550025, China;
3. School of Mathematics and Statistics, Guizhou University, Guiyang 550025, China
开放科学(资源服务)标志码(OSID):
随着大数据技术的快速发展,各类移动设备的计算及通信能力得到显著提高。因此,基于机器学习的新型学习框架应运而生[1]。机器学习技术能够有效提高各类移动设备的应用性能,但是需要将敏感的私有信息和数据上传至中央服务器并对模型进行训练,存在严重的隐私泄露风险、额外的计算与通信开销问题[2-3]。为加强用户数据信息的隐私与安全,联邦学习[4-5]作为一种新型的分布式机器学习技术应运而生。联邦学习使大规模的移动设备在不泄露本地数据的前提下,通过协作使用各自的数据集来训练机器学习共享模型。联邦学习作为一种去中心化分布式的训练模型方法,利用各移动设备的数据采集与计算能力解决数据的隐私安全问题[6]。
由于联邦学习不需要各类移动设备直接进行数据交换,因此在一定程度上保护了用户的数据安全与隐私[7]。文献[8]提出一种基于贪婪算法的联邦学习方案,利用分布式移动设备数据和计算资源来训练高性能机器学习模型,同时保护客户端的隐私和安全。文献[9]通过增强本地移动设备的计算能力减少联邦学习通信频率,设计典型的联邦平均算法,通过云处理中心对局部的移动设备进行整合,大幅减少了传输局部模型的数量,节省通信开销。文献[10]通过无线网络构造联邦学习框架,并对其学习时间和数据的准确度进行优化,以控制用户的数据训练能量成本。文献[11]提出一种三元联邦平均协议,减少联邦学习系统中的上下游通信,该方案从保护物联网设备的隐私和安全出发,在降低通信成本和提高学习性能方面取得一定成效。文献[12]为满足联邦学习的环境需求,提出稀疏三元压缩新的压缩联邦学习框架,解决了在联邦学习训练期间存在通信开销量大的问题。
现有的联邦学习框架假设各移动设备都无条件参与联邦学习[13-14]。在训练数据模型中,各移动设备都会产生相应的训练成本,如果没有激励策略,自私的数据拥有者将不愿意参加联邦学习[15-16]。此外,由于联邦学习中任务发布者不知道参加模型训练的数据拥有者的数据质量,以及可计算资源量,因此任务发布者和数据拥有者之间存在信息不对称的情况。
为进一步考虑理性参与者的存在,文献[17]提出一种参与者是理性参与方的理性证明系统,将博弈论中的理性用户[18-21]引入到各安全协议中。文献[22]研究了计算能力受限的理性参与者问题。
为解决联邦学习的安全隐私与通信开销问题,本文结合Micali-Rabin随机向量表示技术和博弈论框架,提出一种高效的联邦学习方案。根据博弈论激励机制,构建联邦学习的博弈模型,其包括联邦学习的各参与者、效用函数等扩展式博弈各要素。利用Micali-Rabin随机向量表示技术和Pedersen承诺机制保障联邦学习中各参与者训练数据的安全与隐私,以达到全局帕累托最优状态。
1 相关理论 1.1 博弈论本文对博弈论中扩展式博弈和帕累托最优的基本概念进行简单说明。
定义1(扩展式博弈) 博弈论是一门用于数学模型研究理性决策者之间如何互动的学科,参与者之间的互动可能涉及到冲突,也可能涉及到合作。扩展式博弈是个六元组
定义2(帕累托最优) 帕累托最优是将所有资源进行合理分配的一种理想状态,当全局参与者模型达到帕累托最优状态后,不会存在一方的效用利益变好,而另一方的效用收益就会因此而受到损失的情况。在这个状态下,所有的理性参与方都会选择合理的行动策略,使得自己的效用利益最大化,并且全局的效用也是最大化。
如果全局参与者模型达到帕累托最优状态,那么就会满足交换最优、生产最优和产品最优等条件。各个理性参与者在生产交易过程中,即使交换或更改生产条件或者环境,都不会从中再获得利益,从而影响他人利益。各资源已达到理想状态,不存在帕累托改进的状态,即帕累托最优。
1.2 Pedersen承诺机制Pedersen承诺机制是满足无条件秘密性的同态承诺机制,构造承诺机制需要3个阶段:1)初始化阶段,选择任意乘法群
Micali-Rabin随机向量表示技术是基于Pedersen承诺,通过零知识证明技术证明方案中等式的正确性。假设Micali-Rabin随机向量表示技术存在有限域
高效联邦学习博弈模型是结合博弈论与联邦学习,从联邦学习参与方自利的角度出发,通过效用函数来保证联邦学习数据的安全与隐私。为激励具有高质量的数据拥有者积极参加联邦学习,本文基于博弈论框架设计合理有效的激励合约,将各理性参与者贡献的资源映射到适当的货币奖励中。参与者在追求自身利益最大化的同时满足联邦学习全局的利益最大化,从而达到帕累托最优状态。本节设计的高效联邦学习博弈模型包括七元组
联邦学习各个参与者集合
高效联邦学习首先需要建模其方案中各个参与者,在博弈模型中主要存在两类参与方,即联邦学习任务的发布者
在联邦学习博弈模型中存在一些不受任何参与方控制的影响因素,本文将其称为外生随机变量
|
Download:
|
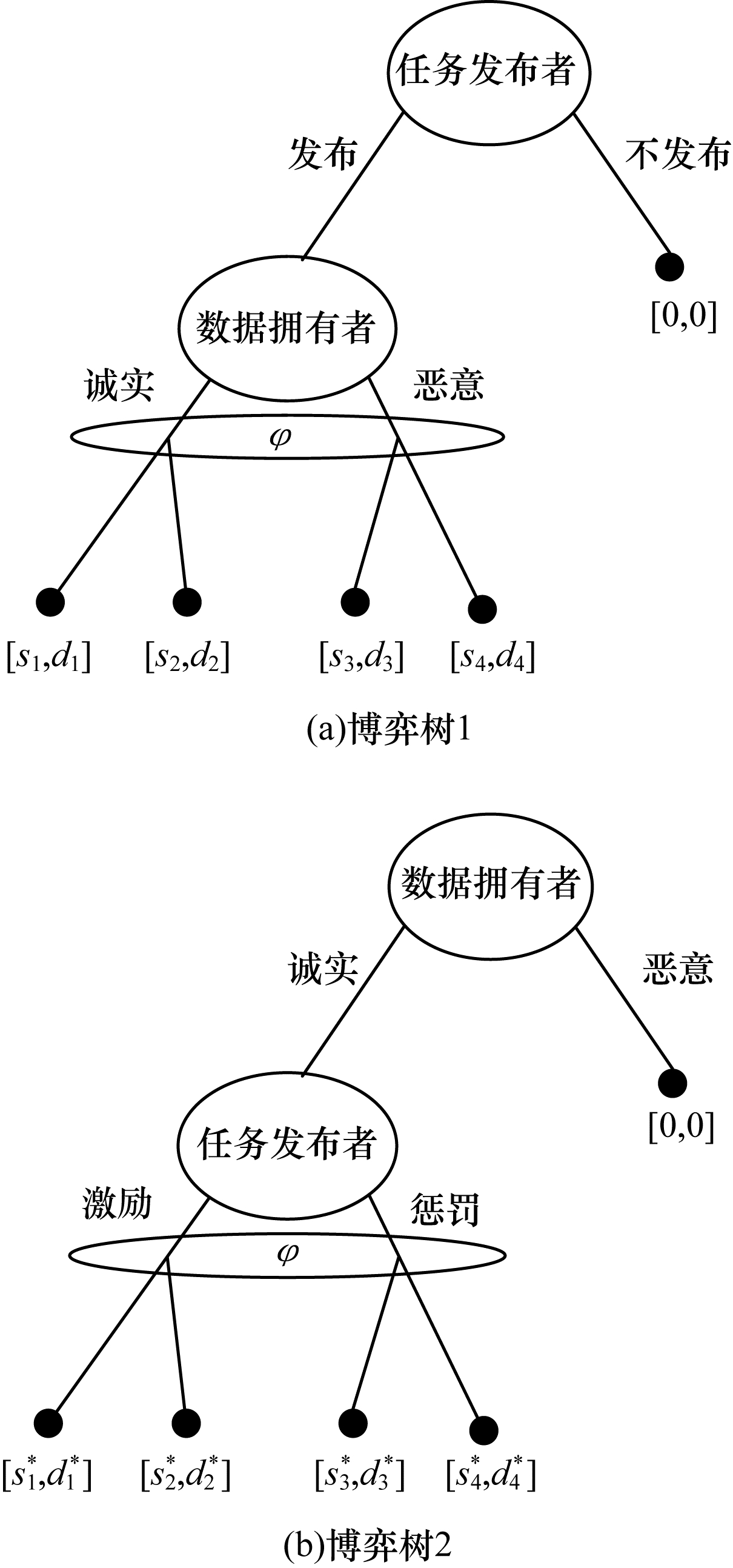
| 图 1 任务发布者与数据拥有者之间博弈树 Fig. 1 Game tree between task publisher and data owner | |
在高效的联邦学习博弈模型中,由于所有参与者都是自利的,因此任务发布者在发布任务后可以选择“激励”或者“惩罚”数据拥有者。令
自私的数据拥有者在接收到任务后可以选择“诚实”或者“恶意”策略进行训练数据与反馈。令
当双方都选择利于自己的行为策略时,且双方都能达到最大效用时,令
在联邦学习博弈模型中,任务发布者通过激励数据拥有者训练数据模型,从而获得高质量数据。因此,本文将任务发布者给予数据拥有者的奖励金额设置为线性函数,如式(1)所示:
| $ {P}_{j}\left(\pi \right)=\alpha +\beta \pi $ | (1) |
其中:
在参与者学习的过程中,参与者将付出一定的努力使得自身的利益最大化,此时会产生相应的努力成本。本文用货币成本来衡量参与者的努力成本,当任务发布者采用不同的策略时,其努力成本如式(2)所示:
| $ C\left({s}_{i}\right)=\frac{1}{2}{x}_{1}{\left(\pi -\eta \pi \right)}^{2} $ | (2) |
同理,数据拥有者采取不同策略时的努力成本如式(3)所示:
| $ C\left({s}_{j}\right)=\frac{1}{2}{x}_{2}{s}_{j}^{2} $ | (3) |
其中:
由于所有的参与者都是理性的,个体间会存在一定的差异性和特殊性,因此各个参与者之间对联邦学习过程中的风险规避程度也会存在一定的差异。在博弈模型中,本文设计的风险规避效用函数为
| $ {P}_{ir}=\frac{1}{2}{\rho }_{1}\mathrm{v}\mathrm{a}\mathrm{r}\left(\pi -{P}_{j}\left(\pi \right)\right)=\frac{1}{2}{\rho }_{1}{\left(1-\beta \right)}^{2}{\sigma }^{2} $ | (4) |
数据拥有者承担风险的成本如式(5)所示:
| $ {P}_{jr}=\frac{1}{2}{\rho }_{2}\mathrm{v}\mathrm{a}\mathrm{r}\left({P}_{j}\left(\pi \right)\right)=\frac{1}{2}{\rho }_{2}{\beta }^{2}{\sigma }^{2} $ | (5) |
其中:
在博弈模型下分析联邦学习方案最关键的是定义参与者的效用函数。在本文方案中,由于参与者都是理性自利且具有风险规避特性,因此其效用函数需要通过参与者的实际收益进行建模。任务发布者的实际收益如式(6)所示:
| $ {v}_{i}=\pi -{P}_{j}\left(\pi \right)-C\left({s}_{i}\right) $ | (6) |
数据拥有者的实际收益如式(7)所示:
| $ {w}_{j}={P}_{j}\left(\pi \right)-C\left({s}_{j}\right) $ | (7) |
根据参与者的实际收益与他们分别存在的风险成本,可以得到任务发布者的期望效用函数,如式(8)所示:
| $ \begin{array}{l}{U}_{i}=E\left(\pi -{P}_{j}\left(\pi \right)-C\left({s}_{i}\right)-{P}_{ir}\right) =\left(1-\beta \right)k{s}_{j}- \\ \alpha -\frac{1}{2}{x}_{1}{\left(1-\eta \right)}^{2}{k}^{2}{s}_{j}^{2}-\frac{1}{2}{\rho }_{1}{\left(1-\beta \right)}^{2}{\sigma }^{2}\end{array} $ | (8) |
同理,数据拥有者的期望效用函数,如式(9)所示:
| $ \begin{array}{l}{U}_{j}=E\left({P}_{j}\left(\pi \right)-C\left({s}_{j}\right)-{P}_{jr}\right)=\\ \alpha +\beta k{s}_{j}-\frac{1}{2}{x}_{2}{s}_{j}^{2}-\frac{1}{2}{\rho }_{2}{\beta }^{2}{\sigma }^{2}\end{array} $ | (9) |
由于联邦学习框架中的参与者都是理性自利的,因此数据拥有者选择与任务发布者签订激励合约后,得到的最大效益必须大于不签署该合约。数据拥有者通过与任务发布者签署激励合约后的期望效用不得小于不接受该任务得到的最小保留效用
| $ \alpha +\beta k{s}_{j}-\frac{1}{2}{x}_{2}{s}_{j}^{2}-\frac{1}{2}{\rho }_{2}{\beta }^{2}{\sigma }^{2}\ge \stackrel{-}{u} $ | (10) |
任务发布者不知道数据拥有者提供的数据质量,在双方存在信息不对称的情况下,并且理性的数据拥有者总会选择使自己期望效用最大化的行为策略。因此,任务发布者希望得到的最大效用通过数据拥有者的最大效用来实现,且全局达到帕累托最优状态。
根据任务发布者和数据拥有者签署的激励合约及帕累托最优状态情况,只有当数据拥有者选择行动策略
| $ {s}_{j}=\frac{\beta k}{x{}_{2}} $ | (11) |
将参与约束IR和激励相容约束IC带入任务发布者期望最大效用的目标函数中,构建拉格朗日函数,可得:
| $ \begin{array}{l} L\left(\alpha , \beta \right)=\left(1-\beta \right)\frac{\beta {k}^{2}}{{x}_{2}}-\alpha -\frac{1}{2}{x}_{1}{\left(1-\eta \right)}^{2}\\ {k}^{2}{\left(\frac{\beta k}{{x}_{2}}\right)}^{2} -\frac{1}{2}{\rho }_{1}{\left(1-\beta \right)}^{2}{\sigma }^{2}+\\ \phi \left(\alpha +\beta k{s}_{j}-\frac{1}{2}{x}_{2}{s}_{j}^{2}-\frac{1}{2}{\rho }_{2}{\beta }^{2}{\sigma }^{2}-\stackrel{-}{u}\right)\end{array} $ | (12) |
将模型中构建的拉格朗日函数
| $ {\beta }^{\mathrm{*}}=\frac{{k}^{2}{x}_{2}+{x}_{2}^{2}{\rho }_{2}{\sigma }^{2}}{{k}^{2}{x}_{2}+{x}_{1}{\left(1-\eta \right)}^{2}{k}^{4}+{x}_{1}\left({\rho }_{1}+{\rho }_{2}\right){\sigma }^{2}} > 0 $ | (13) |
| $ \frac{\partial \beta }{\partial {\rho }_{1}}=\frac{{x}_{2}^{2}{\sigma }^{2}\left({x}_{2}^{2}{\sigma }^{2}{\rho }_{2}+{x}_{2}{\left(1-\eta \right)}^{2}{k}^{4}\right)}{{\left({k}^{2}{x}_{2}+{x}_{1}{\left(1-\eta \right)}^{2}{k}^{4}+{x}_{2}^{2}{\rho }_{2}{\sigma }^{2}\right)}^{2}} > 0 $ | (14) |
根据以上函数的变化趋势可以看出,任务发布者的风险规避程度
| $ {s}_{j}=\frac{k\beta }{{x}_{2}} =\frac{{k}^{3}+{x}_{2}{\rho }_{2}{\sigma }^{2}k}{{k}^{2}{x}_{2}+{x}_{2}{\left(1-\eta \right)}^{2}{k}^{4}+{x}_{2}\left({\rho }_{1}+\rho {}_{2}\right){\sigma }^{2}} $ | (15) |
在联邦学习博弈模型中任务发布者和数据拥有者总的期望效用达到最大,如式(16)所示:
| $ E\left(\pi \right)=\frac{{k}^{4}+{x}_{2}{\rho }_{2}{\sigma }^{2}{k}^{2}}{{k}^{2}{x}_{2}+{x}_{2}{\left(1-\eta \right)}^{2}{k}^{4}+{{x}_{2}}^{2}\left({\rho }_{1}+{\rho }_{2}\right){\sigma }^{2}} $ | (16) |
由此可以看出,在联邦学习模型中,即使任务发布者不知道数据拥有者所选择的行动策略和其努力程度,但是根据双方签署的激励合约,数据拥有者会选择最优的行动策略
本文基于上述设计的联邦学习博弈模型,结合Micali-Rabin随机向量表示技术构造高效安全的联邦学习方案。在本文方案中,各参与者为了使自身利益最大化必须遵循双方签署的激励合约,通过各自的效用函数约束个人理性行为,任何偏离合约的一方都会受到远大于自身成本价值及影响自身声誉的惩罚。
3.1 初始化阶段任务发布者
各数据拥有者
| $ \mathrm{C}\mathrm{O}\mathrm{M}\left({\left({{\theta }_{i}}^{\mathrm{{'}}}\right)}^{l}\right)=\left(\mathrm{C}\mathrm{O}\mathrm{M}\left({u}_{i}^{l}\right), \mathrm{C}\mathrm{O}\mathrm{M}\left({v}_{i}^{l}\right)\right) $ |
| $ {\left({\theta }_{i}^{{'}}\right)}^{l}=\left({u}_{i}^{l}, {v}_{i}^{l}\right) \text{,} \mathrm{v}\mathrm{a}\mathrm{l}\left({\left({{\theta }_{i}}^{\mathrm{{'}}}\right)}^{l}\right)=\left({u}_{i}^{l}+{v}_{i}^{l}\right)\mathrm{m}\mathrm{o}\mathrm{d}\;p \text{,} $ |
| $ 1\le l\le 3k $ | (17) |
在这个阶段中要求任意概率多项式时间的接收方都不能获取有关承诺的任何信息,以保护所有数据的隐私和安全,。
3.3 聚合验证阶段中央服务器接收各个数据拥有者返回的更新参数
任务发布者
当任务发布者
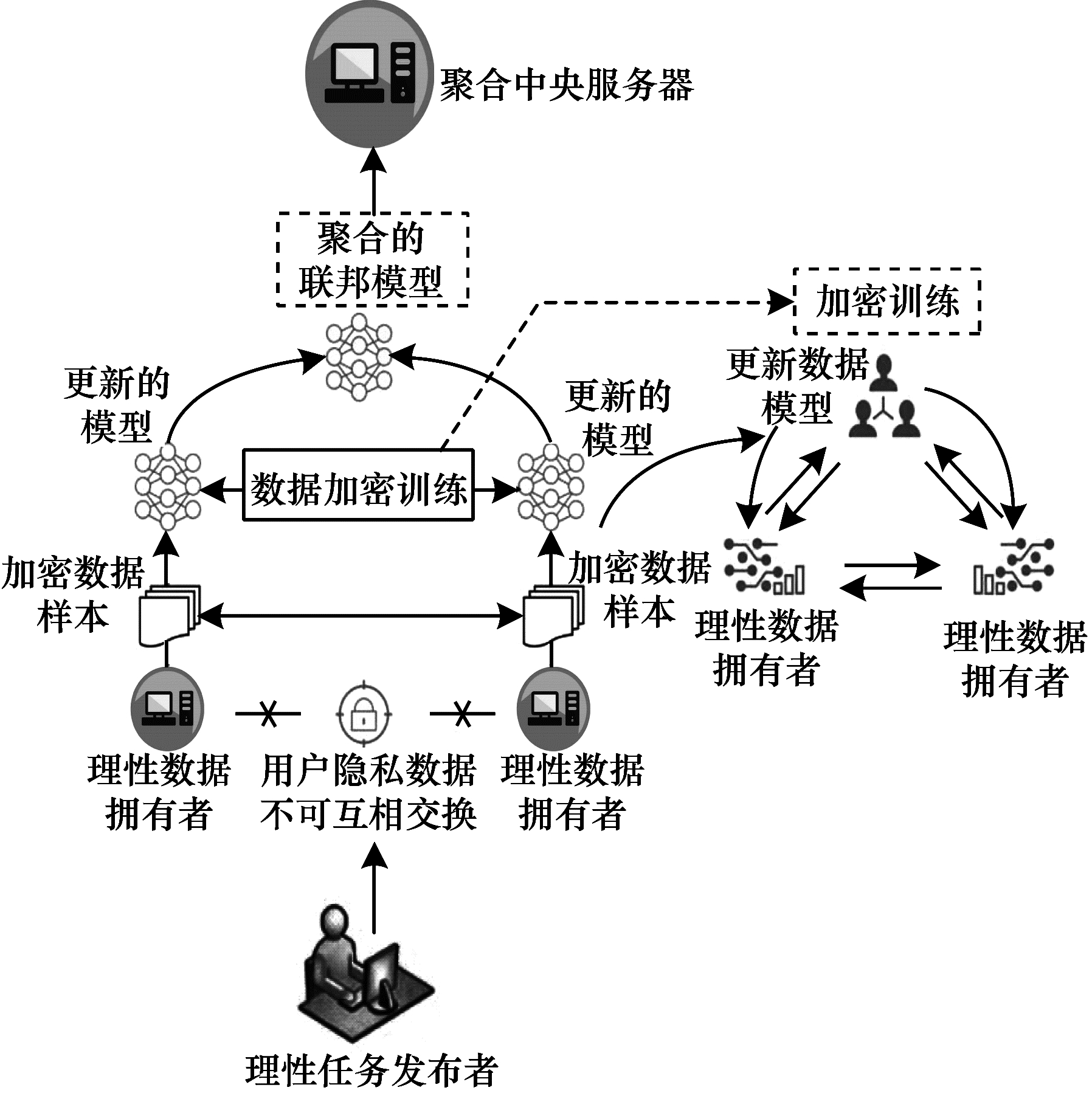
由于构造的方案中各方参与者都是理性自利的,他们会为了使自身利益得到最大化选择最优的行动策略。在该方案中,根据双方签署的激励合约,一旦有参与者选择偏离方案的恶意行为,将会受到严重的资金惩罚。各参与方通过激励合约约束并激励自己遵守方案,降低各参与方通信的风险,并提高联邦学习的通信效率。高效联邦学习系统架构如图 2所示。
|
Download:
|
| 图 2 高效联邦学习系统架构 Fig. 2 Architecture of efficient federated learning system | |
本文从安全性分析基于博弈论优化的高效联邦学习方案。
定理1 本文联邦学习方案具有安全性。
证明 在联邦学习的本地训练阶段中,各数据拥有者采用Micali-Rabin随机向量表示技术对承诺值
假设本文方案是不安全的,那么会存在恶意参与者将返回至中央服务器的承诺值进行篡改
本文从正确性分析基于博弈论优化的高效联邦学习方案。
定理2 本文联邦学习方案具有正确性。
证明 本文联邦学习方案中,如果任务发布者
由于双方都是理性的,在方案中为了自身利益最大化不会选择不利于自己的行动策略,只有双方都选择最优策略,全局才能达到最优状态
本文从公平性分析基于博弈论优化的高效联邦学习方案。
定理3 本文联邦学习方案具有公平性。
证明 在高效联邦学习方案中,所有参与者都是理性自私的,为了自身利益的最大化可以随意选择自己的行动策略。为保证本文方案的公平性,在方案的初始化阶段中,任务发布者需要与数据拥有者签署激励合约,严格按照合约的要求执行。
双方选择的策略在激励合约中的取值为“0”或“1”。一种情况是双方根据自己的效用函数
不同方案的安全性、正确性和公平性对比如表 1所示,其中,“√”表示方案满足上述性质,“×”表示方案不满足上述性质。

|
下载CSV 表 1 不同方案的性能对比 Table 1 Performances comparison among different schemes |
从表 1可以看出,现有的大多数联邦学习方案考虑方案的安全性,但是通常认为参与者都是诚实的,未考虑到参与者的自利行为,即对方案的公平性方面考虑的较少,这也是影响联邦学习效率与应用的原因之一。
5 实验仿真本文借鉴文献[24]的数字分类数据集MINIST对本文方案进行模拟评估。本文选择60 000条训练数据示例,其中包含1个任务发布者和50个数据拥有者,用于执行数据训练分类任务。数据拥有者首先与可以接受模型训练的数据拥有者签订激励合约。签订合约的数据拥有者根据任务发布者上传的任务,随机分配需要训练的数据集,并作为本地的训练数据。
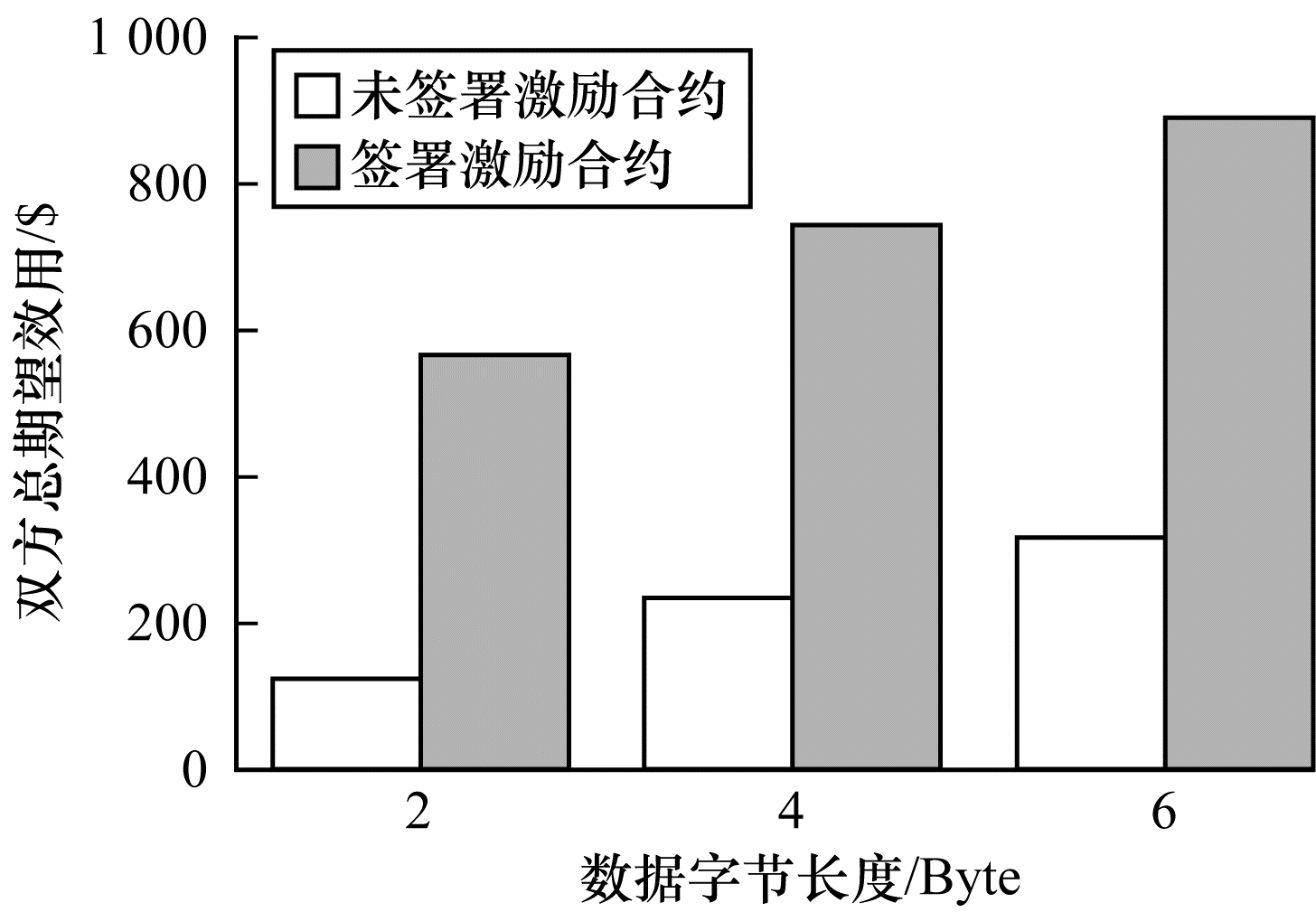
为验证激励合约的有效性,本文分别对签署和未签署激励合约的参与者进行联邦学习,并对拥有不同数据字节长度的拥有者利益和任务发布者的利益关系进行分析讨论。签署与未签署激励合约的总期望效用对比如图 3所示。从图 3可以看出,当拥有者的数据字节长度分别为2、4和6 Byte时,无论数据类型为何种的数据拥有者,他们与任务发布者之间的效用只有当都选择签署激励合约时,双方的效用才最大,此时方案全局的利益也最大,即达到帕累托最优状态。
|
Download:
|
| 图 3 签署与未签署激励合约的总期望效用对比 Fig. 3 Total expected utility comparison of signed and unsigned incentive contracts | |
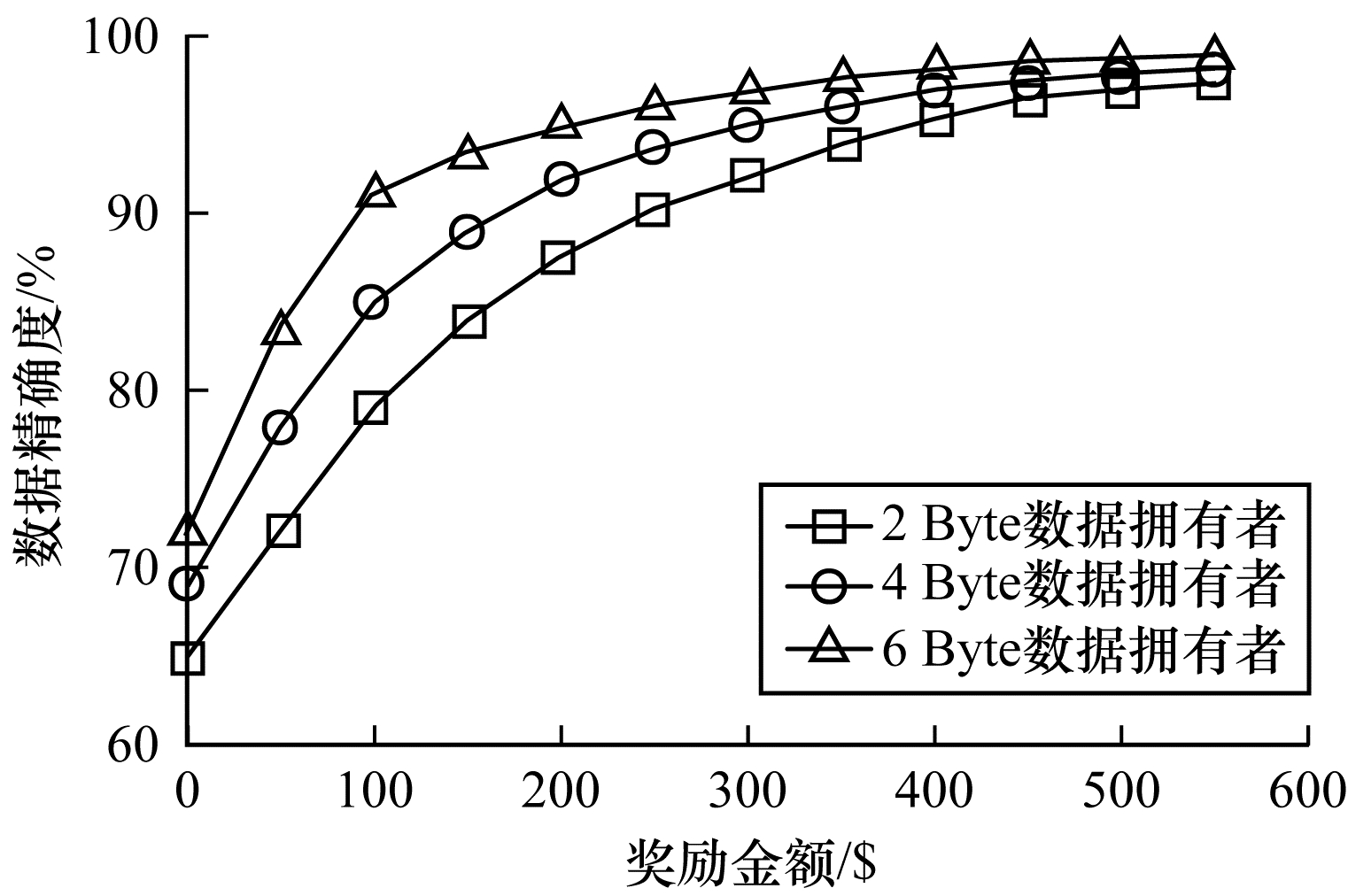
本文对任务发布者和数据拥有者的激励策略进行分析,确定任务发布者给予的激励金额大小与数据训练精确度之间的关系。数据的精确度随奖励金额的变化趋势如图 4所示。随着任务发布者提供的激励奖励的增加,拥有不同数据类型数据拥有者的数据训练精确度从65%逐步提高至98%。在本文激励合约下,当任务发布者的激励奖励越高时,越能激励数据拥有者进行模型训练,最终获得的数据质量也越高,从而实现高效的联邦学习。
|
Download:
|
| 图 4 不同奖励金额下数据的精确度 Fig. 4 Accuracy of data under different reward amounts | |
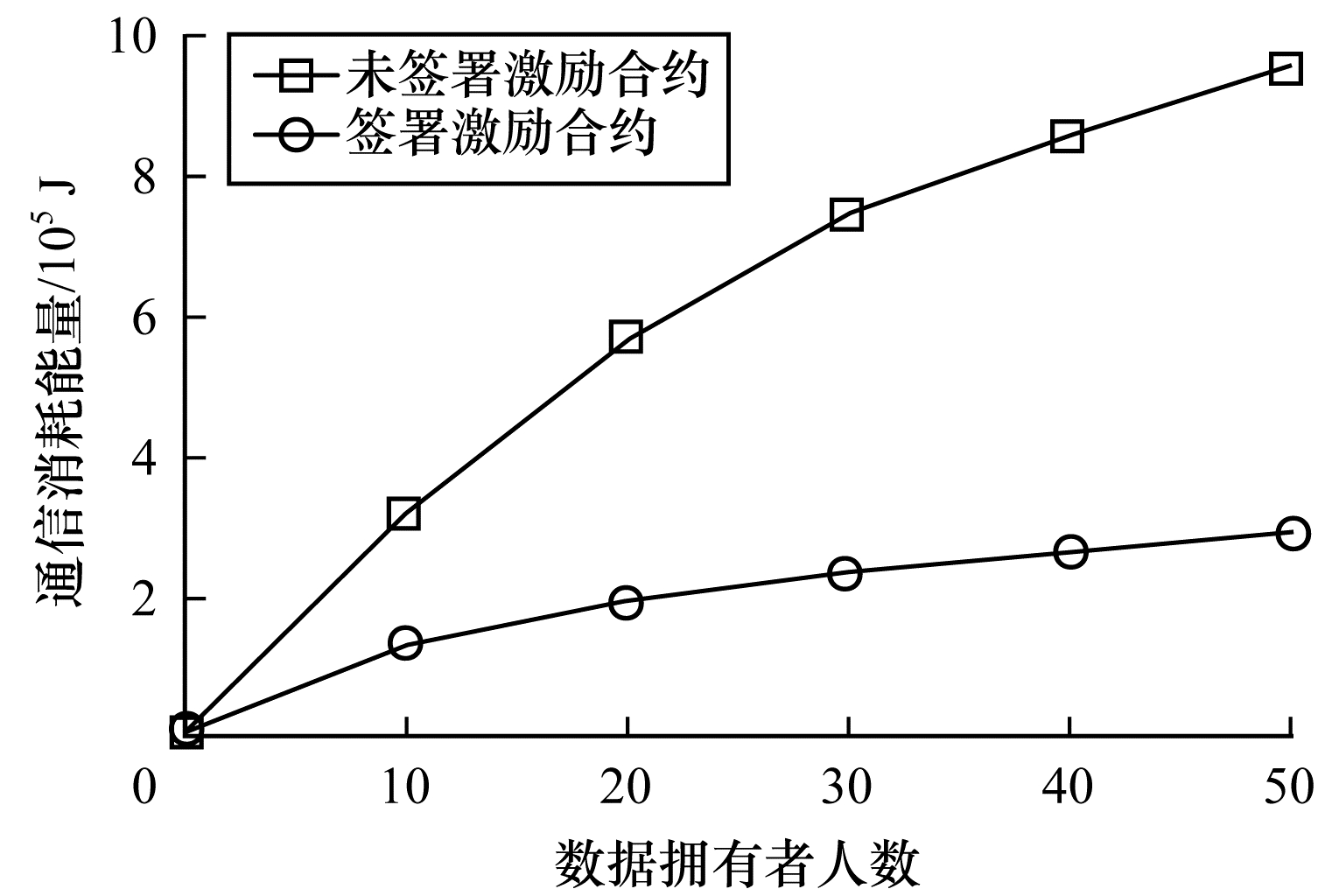
签署与未签署激励合约拥有者的通信消耗能量对比如图 5所示。当未签署与签署激励合约的数据拥有者从0~50逐渐增加时,其通信开销发生了很大的变化。从图 5可以看出:当参与者未签署激励合约时,其数据拥有者越多,通信开销越大;有激励合约的参与者通信开销几乎无变化,验证了本文联邦学习方案的高效性。
|
Download:
|
| 图 5 签署与未签署激励合约拥有者的通信消耗能量对比 Fig. 5 Energy consumption of communication comparison of owner with and without incentive contracts | |
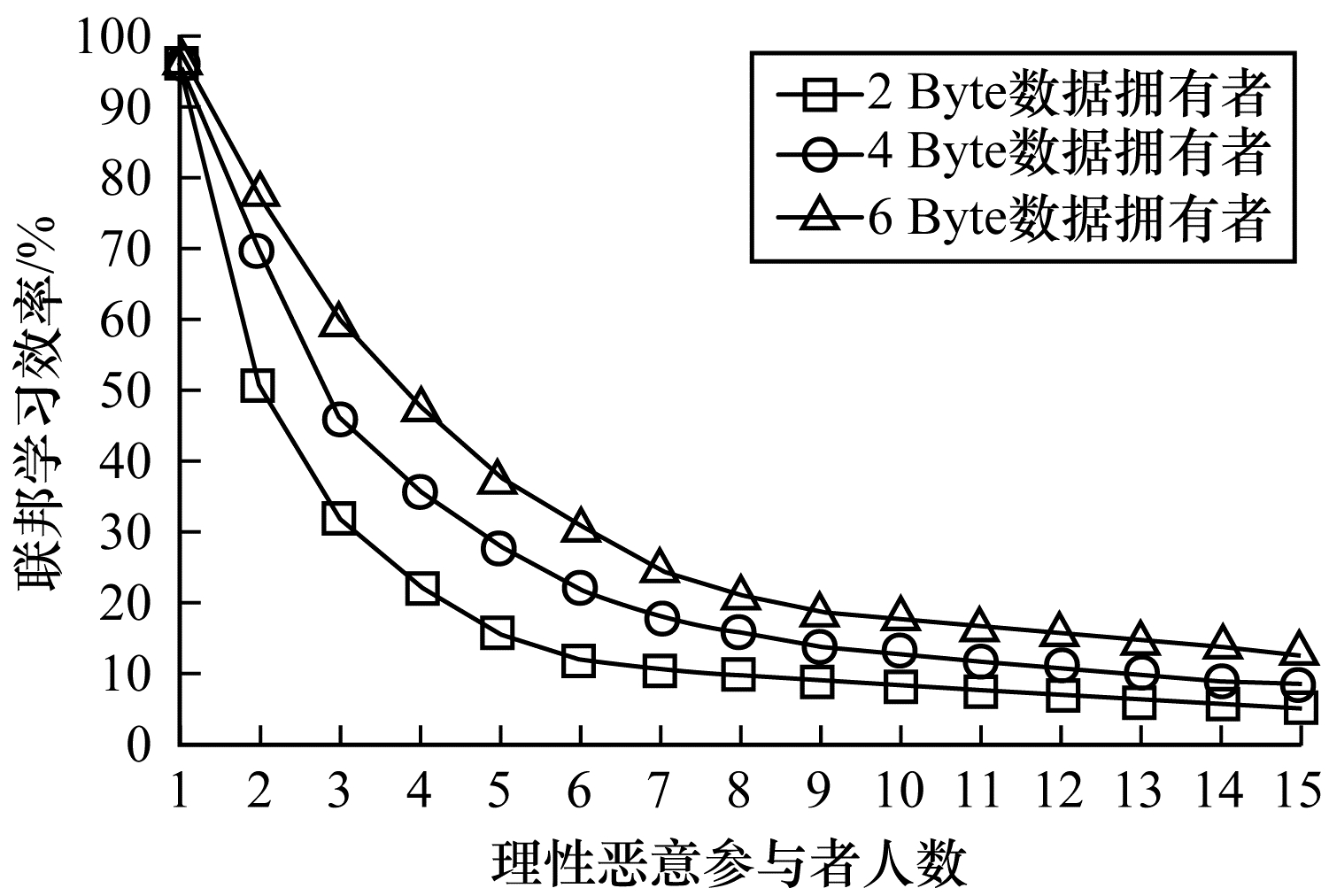
本文方案性能的影响因素是参与者的自利性行为。若参与者是自私恶意的,在方案执行过程中,由双方的激励合约可知,双方将根据效用函数对自私恶意的参与者进行惩罚,并且阻止方案继续执行。不同参与者行为联邦学习效率变化如图 6所示。当拥有不同数据类型的参与者若存在自私恶意的数据拥有者,方案的效率将降低。
|
Download:
|
| 图 6 不同参与者的联邦学习效率对比 Fig. 6 Efficiency of federated learning comparison among different participants | |
本文设计的方案中用户的奖励越大,其选择积极策略的可能性越大,获得的数据准确度也越高,用户的通信消耗量远远小于用户未签署激励合约的通信量。当拥有不同数据类型的参与者存在理性恶意的数据拥有者时,极大影响联邦学习的效率,从而影响双方效用收益。因此,本文设计的方案是有效的。
6 结束语本文提出基于博弈论优化的高效联邦学习方案,利用博弈论激励高质量的数据拥有者和任务发布者,同时结合Micali-Rabin随机向量表示技术和Pedersen承诺方案,实现高效联邦学习的隐私保护。仿真结果表明,该方案不仅使得全局参与者达到帕累托最优状态,而且为联邦学习的各参与者的利益和数据隐私提供了保证。后续将在多任务者同时发布模型训练任务的前提下,从不同的角度和应用场景中研究联邦学习,进一步提高学习效率。
| [1] |
YANG Q, LIU Y, CHEN T J, et al. Federated machine learning: concept and applications[EB/OL]. [2021-07-15]. https://arxiv.org/pdf/1902.04885.pdf.
|
| [2] |
PAPERNOT N, ABADI M, ERLINGSSON Ú, et al. Semi-supervised knowledge transfer for deep learning from private training data[EB/OL]. [2021-07-15]. https://arxiv.org/abs/1610.05755.
|
| [3] |
ZHU X D, LI H, YU Y. Blockchain-based privacy preserving deep learning[C]//Proceedings of International Conference on Information Security and Cryptology. Berlin, Germany: Springer, 2018: 1-10.
|
| [4] |
BARAI A K, BHADORIA R S, BAGWARI J, et al. A blockchain-based federated learning: concepts and applications[M]//DEKA G C. Multidisciplinary functions of blockchain technology in AI and IoT applications. Hershey, USA: IGI Global Press, 2021: 158-177.
|
| [5] |
YANG W, ZHANG Y, WEI Y, et al. Privacy is not free: energy-aware federated learning for mobile and edge intelligence[C]//Proceedings of International Conference on Wireless Communications and Signal Processing. Zhengzhou, China: [s. n. ], 2020: 1-10.
|
| [6] |
POSNER J, TSENG L, ALOQAILY M, et al. Federated learning in vehicular networks: opportunities and solutions[J]. IEEE Network, 2021, 35(2): 1-8. DOI:10.1109/MNET.2021.9387949 |
| [7] |
GEYER R C, KLEIN T, NABI M. Differentially private federated learning: a client level perspective[EB/OL]. [2021-07-15]. https://arxiv.org/abs/1712.07557.
|
| [8] |
YOSHIDA N, NISHIO T, MORIKURA M, et al. MAB-based client selection for federated learning with uncertain resources in mobile networks[EB/OL]. [2021-07-15]. https://arxiv.org/abs/2009.13879.
|
| [9] |
MCMAHAN H B, MOORE E, RAMAGE D, et al. Communication-efficient learning of deep networks from decentralized data[EB/OL]. [2021-07-15]. https://arxiv.org/pdf/1602.05629.pdf.
|
| [10] |
TRAN N H, BAO W, ZOMAYA A, et al. Federated learning over wireless networks: optimization model design and analysis[C]//Proceedings of IEEE Conference on Computer Communications. Washington D. C., USA: IEEE Press, 2019: 1-10.
|
| [11] |
FELIX S, SIMON W, KLAUS-ROBERT M, et al. Robust and communication-efficient federated learning from non-i. i. d. data[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(9): 3400-3413. |
| [12] |
MALEKIJOO A, FADAEIESLAM M J, MALEKIJOU H, et al. FEDZIP: a compression framework for communication-efficient federated learning[EB/OL]. [2021-07-15]. https://arxiv.org/abs/2102.01593.
|
| [13] |
SHAYAN M, FUNG C, YOON C, et al. Biscotti: a blockchain system for private and secure federated learning[J]. IEEE Transactions on Parallel and Distributed Systems, 2020, 99: 1-10. |
| [14] |
CHEN H, ASIF S A, PARK J, et al. Robust blockchained federated learning with model validation and proof-of-stake inspired consensus[EB/OL]. [2021-07-15]. https://arxiv.org/abs/2101.03300.
|
| [15] |
QU Y Y, POKHREL S R, GARG S, et al. A blockchained federated learning framework for cognitive computing in industry 4.0 networks[J]. IEEE Transactions on Industrial Informatics, 2020, 99: 1-10. |
| [16] |
PENG Z, XU J, CHU X, et al. VFChain: enabling verifiable and auditable federated learning via blockchain systems[J]. IEEE Transactions on Network Science and Engineering, 2021, 99: 1-10. |
| [17] |
AZAR P D, MICALI S. Rational proofs[C]//Proceedings of the 44th Annual ACM Symposium on Theory of Computing. New York, USA: ACM Press, 2012: 1017-1028.
|
| [18] |
李朋, 陶洋, 许湘扬, 等. 基于博弈论的无线传感器网络能耗均衡分簇协议[J]. 计算机工程, 2018, 44(12): 156-162. LI P, TAO Y, XU X Y, et al. Energy consumption balance clustering protocol in wireless sensor network based on game theory[J]. Computer Engineering, 2018, 44(12): 156-162. (in Chinese) |
| [19] |
CHEN J, MCCAULEY S, SINGH S. Rational proofs with multiple provers[C]//Proceedings of ACM Conference on Innovations in Theoretical Computer Science. New York, USA: ACM Press, 2016: 237-248.
|
| [20] |
田有亮, 马建峰, 彭长根, 等. 秘密共享体制的博弈论分析[J]. 电子学报, 2011, 39(12): 2790-2795. TIAN Y L, MA J F, PENG C G, et al. Game-theoretic analysis for the secret sharing scheme[J]. Acta Electronica Sinica, 2011, 39(12): 2790-2795. (in Chinese) |
| [21] |
李秋贤, 田有亮, 王缵. 基于全同态加密的理性委托计算协议[J]. 电子学报, 2019, 47(2): 216-220. LI Q X, TIAN Y L, W Z. Rational delegation computation protocol based on fully homomorphic encryption[J]. Acta Electronica Sinica, 2019, 47(2): 216-220. (in Chinese) |
| [22] |
GUO S, HUBACEK P, ROSEN A, et al. Rational arguments: single round delegation with sublinear verification[C]//Proceedings of the 5th Conference on Innovations in Theoretical Computer Science. New York, USA: ACM Press, 2014: 523-540.
|
| [23] |
KIM H, PARK J, BENNIS M, et al. On-device federated learning via blockchain and its latency analysis[EB/OL]. [2021-07-15]. https://arxiv.org/abs/1808.03949.
|
| [24] |
KANG J W, XIONG Z H, NIYATO D, et al. Incentive design for efficient federated learning in mobile networks: a contract theory approach[C]//Proceedings of IEEE VTS Asia Pacific Wireless Communications Symposium. Washington D. C., USA: IEEE Press, 2019: 1-10.
|
 2022, Vol. 48
2022, Vol. 48

 ,
,