2. 西安邮电大学 电子工程学院, 西安 710121;
3. 西安邮电大学 理学院, 西安 710121
2. School of Electronic Engineering, Xi'an University of Posts and Telecommunications, Xi'an 710121, China;
3. School of Science, Xi'an University of Posts and Telecommunications, Xi'an 710121, China
开放科学(资源服务)标志码(OSID):
图像分割是根据低层特征的相似性或相异性将图像分割成若干个连续的子区域,使同一区域内的特征相似,而不同区域内的特征相异。图像分割方法可大致分为基于边缘[1]、基于阈值[2]、基于聚类[3-4]、基于区域[5]、基于图论[6]的5类方法。其中聚类是一种无监督分类方法[7],在像素没有标签的情况下,利用类间差别尽可能大而类内差别尽可能小的原则将原像素划分成不同的类,分为硬聚类[8]和模糊聚类[9]。硬聚类强调每个像素数据只能被归为一类,模糊聚类通过隶属度来强调每个像素数据属于每一类的程度,而不是硬性地将数据归到某一类。聚类分析的核心是利用数学方法将目标样本集按某种准则自动归为若干个互不重叠的类,使同一类中的样本相似,不同类中的样本互不相同,这一思想与图像分割相似。模糊聚类应用于分割问题时,引入隶属度表示样本属于某个特定集合的确定程度,体现了描述的模糊性。
在众多的模糊聚类算法中,模糊C-均值(Fuzzy C-Means,FCM)聚类算法[10]是较为经典的无监督聚类算法,考虑了像素对各个聚类中心的隶属度,但并未考虑像素本身和邻域像素之间的关联性,对于含噪图像的聚类难以获得满意的分割结果。为了增强FCM算法的抗噪性,AHMED等[11]将局部空间限制项引入FCM目标函数,提出一种基于空间信息的FCM算法(FCM_S),由于该算法在每次迭代计算过程中都需要计算像素的邻域项,因此时效性较差。CHEN等[12]提出两种FCM_S的改进方法:FCM_S1和FCM_S2算法,这两种算法分别采用邻域像素的灰度均值和灰度中值来表示像素的局部空间信息,从而有效提高了算法的计算效率。KRINIDIS等[13]利用像素点的局部信息构造空间模糊因子,并引入FCM提出模糊局部信息C-均值(Fuzzy Local Information C-Means,FLICM)聚类算法,该算法相比于FCM_S无需人为设置算法中的参数,能自适应控制噪声的干扰和保留图像细节信息间的平衡。ZHANG等[14]引入包含非局部信息的像素相关度代替FLICM算法中的空间约束并改进模糊因子,提出非局部信息模糊C-均值聚类算法(Non-Local information Fuzzy C-Means,NLFCM),该算法有较好的抗噪性,但却抹去了图像的部分细节信息。
传统FCM算法利用欧式距离来计算像素到聚类中心的距离,原理是将像素空间中较为相近的像素聚在一起,仅适合聚类像素数目相差不悬殊的团状凸数据集,对于复杂的非凸数据集,聚类性能急剧下降。为此,很多学者将核函数[15]的思想引入FCM算法,提出核模糊C-均值(Kernal Fuzzy C-Means,KFCM)聚类算法[16],该算法将像素数据通过非线性函数映射至高维特征空间,使得原空间线性不可分的像素变得线性可分,以此来改善聚类性能。由于高斯核函数的控制参数较少且性能较稳定,因此相比其他核函数应用更广泛。GONG等[17]在FLICM算法的基础上进行改进,提出一种基于核度量的加权模糊局部信息C-均值(Kernel metric-based Weighted Fuzzy Local Information C-Means,KWFLICM)聚类算法。该算法利用空间差异性定义一个加权平衡模糊因子,包含了图像邻域像素的空间距离约束信息和空间灰度约束信息,并采用高斯核空间距离代替像素点间的欧式距离,提高了算法对噪声的鲁棒性。但由于引入过多的邻域信息,因此使得图像的部分细节信息被抹去。
BUADES等[18]提出非局部均值(Non-Local Means,NLM)图像去噪方法,采用图像块间的欧式距离确定像素点间的相似度权重,通过像素点间的加权平均实现均值滤波效果。引导滤波器[19]在一定程度上可以起到保边去噪的作用,且计算效率高,十分适合弱过滤工作[20],因此众多学者将引导滤波与模糊聚类算法相结合来提高模糊聚类算法的分割性能。引导滤波利用引导图像的信息对输入的图像进行滤波处理得到输出图像,相当于一个局部线性转换器使得输出和输入呈线性关系[21]。考虑到引导滤波保边平滑的特点,GUO等[22]提出图像引导模糊C-均值(Image Guided Fuzzy C-Means,IGFCM)聚类算法。在该算法中的引导滤波作为正则项加入模糊C-均值算法的目标函数,从而根据引导图像的信息对隶属度进行约束,但由于模型复杂难以计算,因此未得到很好的应用。为了简化IGFCM算法,GUO等[23-24]提出基于引导滤波的改进模糊C-均值(modified FCM with Guided Filtering,FCM+GF)方法,在该方法中将需要分割的图像作为引导图像,对模糊C-均值聚类算法得到的隶属度进行处理,但该方法对强噪声图像分割结果并不理想,且仅限于灰度图像分割。对于彩色图像,执行多通道的引导滤波是一项困难的工作,鉴于此问题,XU等[25]提出一种加权多通道引导滤波(Weighting Multi-channel Guided image Filtering,WMGF)算法来提高边缘保护,降低计算复杂度,基于该算法又提出一种新的彩色图像模糊C-均值聚类算法(FCMWMGF),为了进一步提高不同噪声的抗噪性和边缘保护性,将多元形态重建方法[26-27]引入改进的模糊C-均值聚类算法(MMR_FCMWMGF)来获得更高的分割精度,该算法对于彩色图像具有较好的分割效果。LIU等[28]提出一种鲁棒引导图像滤波(Robust Guided Image Filtering,RGIF)技术,将一个数据项和平滑项组成的优化框架融入引导滤波。SHEN等[29]考虑输入图与引导图结构的不一致性,提出一种相互结构联合滤波算法并得到了较好的结果。
上述方法对于引导滤波的利用都是通过像素对模糊聚类算法得到的隶属度进行引导,然而该方法仅适用于处理低噪声图像。为了提高基于引导滤波的模糊聚类算法的分割性能和抑噪能力,本文将像素引导隶属度和隶属度引导像素的交替引导滤波引入KWFLICM算法,提出一种新的基于交替引导滤波的鲁棒模糊聚类算法GFKWFLICMGF。
1 相关工作 1.1 引导滤波引导滤波是一种线性滤波器,基本思想是:在图像梯度比较大的地方实现保边,要求尽量不平滑,最好是输出与输入一样;在图像梯度较小的地方尽量平滑,输出与输入可以稍有不同。假设输入图为
| $ {X}_{j}^{\text{'}}={a}_{i}{I}_{j}+{b}_{i} \text{,} \forall j\in {w}_{i} $ | (1) |
其中:
| $ E({a}_{i}, {b}_{i})=\sum\limits _{j\in {w}_{i}}\left(\right({a}_{i}{I}_{j}+{b}_{i}-{X}_{j}{)}^{2}+\varepsilon {a}_{i}^{2}) $ | (2) |
其中:
| $ {a}_{i}=\left(\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{I}_{j}{X}_{j}-{\stackrel{-}{I}}_{i}{\stackrel{-}{X}}_{i}\right)/(\varepsilon +{s}_{i}^{2}) $ | (3) |
| $ {b}_{i}={\stackrel{-}{x}}_{i}-{a}_{i}{\stackrel{-}{I}}_{i} $ | (4) |
其中:
| $ {X}_{j}^{\text{'}}={\stackrel{-}{a}}_{i}{I}_{j}+{\stackrel{-}{b}}_{i} $ | (5) |
通过式(5)可以看出
当输入图像自身作为引导图时,
FLICM算法通过模糊因子
| $ {J}_{m}(\boldsymbol{U}, \boldsymbol{V})=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}{\mu }_{ik}^{m}\left[\right(1-K({x}_{i}, {v}_{k}))+{G}_{ik}^{\text{'}}] $ | (6) |
其中:
权重系数
| $ {G}_{ik}^{\text{'}}=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}{\mu }_{ik}^{m}\sum\limits _{\underset{j\in {w}_{i}}{j\ne i}}{w}_{ij}(1-{\mu }_{jk}{)}^{m}(1-K({x}_{j}, {v}_{k})) $ | (7) |
权重因子
| $ \begin{array}{l}{\mu }_{ik}=\\ \frac{1}{\sum\limits _{l=1}^{c}{\left[\frac{\left(\right(1-K({x}_{i}, {v}_{k}))\mathrm{ }+\sum\limits _{j\in {N}_{i}, j\ne i}{w}_{ij}(1-{\mu }_{jk}{)}^{m}(1-K({x}_{j}, {v}_{k}))}{\left(\right(1-K({x}_{i}, {v}_{l}))\mathrm{ }+\sum\limits _{j\in {N}_{i}, j\ne i}{w}_{ij}(1-{\mu }_{jl}{)}^{m}(1-K({x}_{j}, {v}_{l}))}\right]}^{1/(m-1)}}\end{array} $ | (8) |
| $ {v}_{k}=\sum\limits _{i=1}^{n}\left({\mu }_{ik}^{m}K\right({x}_{i}, {v}_{k}\left){x}_{i}\right)/\sum\limits _{i=1}^{n}\left({\mu }_{ik}^{m}K\right({x}_{i}, {v}_{k}\left)\right) $ | (9) |
像素引导隶属度滤波的目的是得到新的隶属度,并使用新的隶属度矩阵作为划分矩阵来对图像进行聚类,目标函数如下:
| $ E(\boldsymbol{U}, \boldsymbol{p}, \boldsymbol{q})=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}\sum\limits _{j\in {w}_{i}}\left[\right({p}_{ik}{I}_{j}+{q}_{ik}-{\mu }_{jk}{)}^{2}+\varepsilon {p}_{ik}^{2}] $ | (10) |
其中:
该目标函数分别对
| $ {q}_{ik}={\stackrel{-}{\mu }}_{ik}-{p}_{ik}{\stackrel{-}{I}}_{i} $ | (11) |
| $ {p}_{ik}=\frac{\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{\mu }_{jk}{I}_{j}-\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{\mu }_{jk}\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{I}_{j}}{\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{I}_{j}^{2}-\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{I}_{j}\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{I}_{j}+\varepsilon } $ | (12) |
其中:
根据方差公式
| $ {p}_{ik}=\left(\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{\mu }_{jk}{I}_{j}-{\stackrel{-}{\mu }}_{ik}{\stackrel{-}{I}}_{i}\right)/({s}_{i}^{2}+\varepsilon ) $ | (13) |
隶属度引导像素滤波的目的是得到新的像素值,将模糊聚类得到的隶属度传入利用隶属度引导像素滤波的代价函数,得到引导滤波的线性系数
| $ {E}_{1}(\boldsymbol{U}, {\boldsymbol{p}}_{1}, {\boldsymbol{q}}_{1})=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}\sum\limits _{j\in {w}_{i}}\left[\right({p}_{1i}{\mu }_{jk}+{q}_{1i}-{I}_{j}{)}^{2}+\varepsilon {p}_{1i}^{2}] $ | (14) |
其中:
该目标函数分别对
| $ {q}_{1i}={\stackrel{-}{I}}_{i}-{p}_{1i}{\stackrel{-}{\mu }}_{ik} $ | (15) |
| $ {p}_{1i}=\frac{\sum\limits _{k=1}^{c}\left(\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{I}_{j}\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{\mu }_{jk}\right)}{\sum\limits _{k=1}^{c}\left(\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{\mu }_{jk}^{2}-{\left(\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{\mu }_{jk}\right)}^{2}\right)+\varepsilon } $ | (16) |
令
| $ {p}_{1i}=\left(\frac{1}{\left|{n}_{w}\right|}\sum\limits _{j\in {w}_{i}}{\mu }_{jk}{I}_{j}-{\stackrel{-}{\mu }}_{ik}{\stackrel{-}{I}}_{i}\right)/({s}_{1i}^{2}+\varepsilon ) $ | (17) |
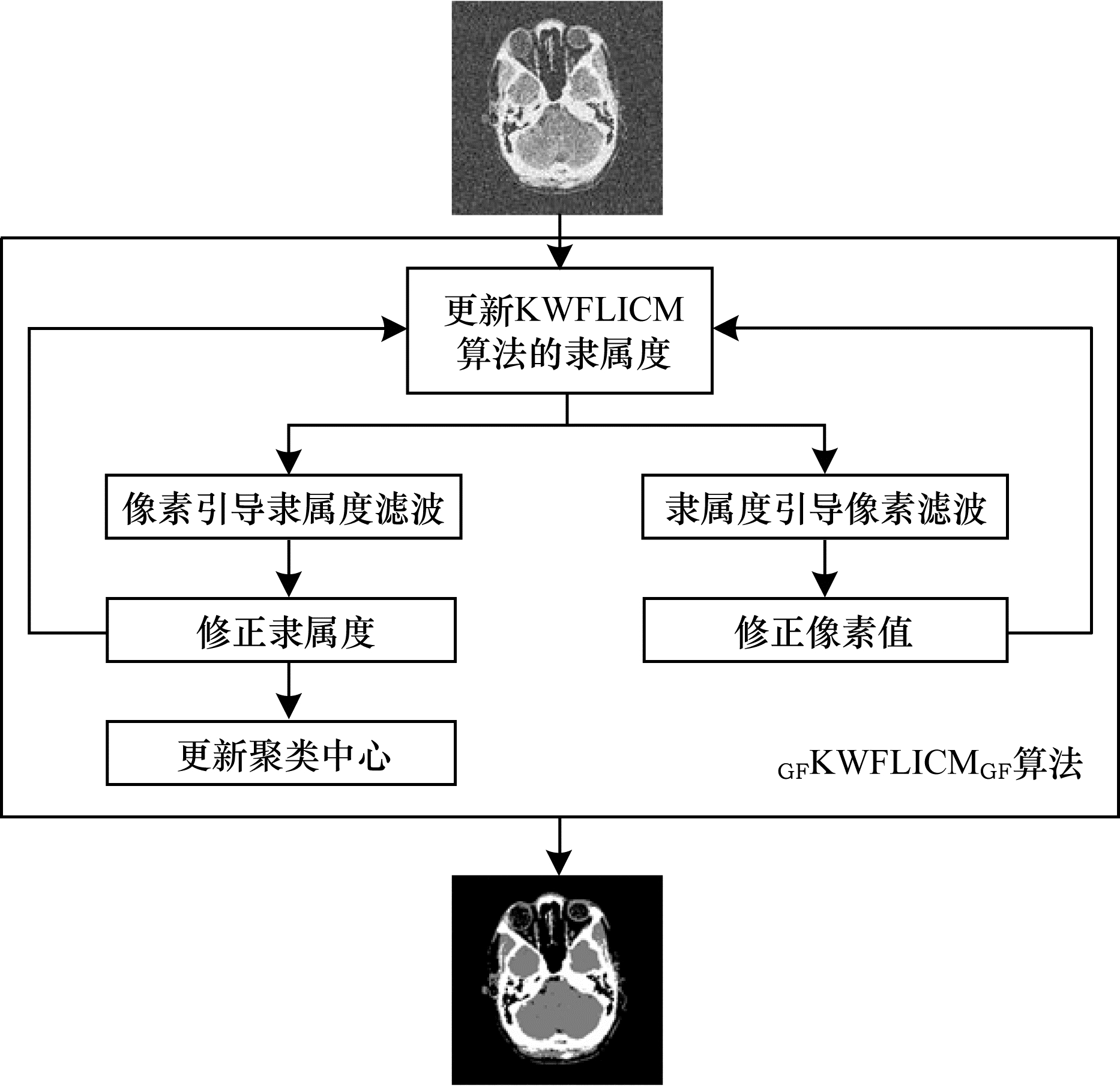
GFKWFLICMGF算法流程如图 1所示。原始加噪图像被当作引导图像,先利用KWFLICM算法对原始加噪图像进行聚类,将得到的隶属度分别传入像素引导隶属度滤波和隶属度引导像素滤波模块,分别得到新的隶属度和新的像素值,并通过新的隶属度对聚类中心进行更新,再将更新后的隶属度和像素值传入KWFLICM算法,循环上述过程,直到算法收敛。
|
Download:
|
| 图 1 GFKWFLICMGF算法流程 Fig. 1 Procedure of GFKWFLICMGF algorithm | |
GFKWFLICMGF算法的迭代过程即优化以下多目标函数的过程:
| $ \begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}{J}_{m}(\boldsymbol{U}, \boldsymbol{V})\mathrm{ }=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}{\mu }_{ik}^{m}\left[\right(1-K({x}_{i}, {v}_{k}))+{G}_{ik}^{\text{'}}]\\ E(\boldsymbol{U}, \boldsymbol{p}, \boldsymbol{q})\mathrm{ }=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}\sum\limits _{j\in {w}_{i}}\left[\right({p}_{ik}{I}_{j}+{q}_{ik}-{\mu }_{jk}{)}^{2}+\varepsilon {p}_{ik}^{2}]\\ L\left({\boldsymbol{\mu }}^{\text{'}}\right)\mathrm{ }=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}\sum\limits _{j\in {w}_{i}}({p}_{jk}{x}_{i}+{q}_{jk}-{\mu }_{ik}^{\text{'}}{)}^{2}\\ {E}_{1}(\boldsymbol{U}, {\boldsymbol{p}}_{1}, {\boldsymbol{q}}_{1})\mathrm{ }=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}\sum\limits _{j\in {w}_{i}}\left[\right({p}_{1i}{\mu }_{jk}+{q}_{1i}-{I}_{j}{)}^{2}+\varepsilon {p}_{1i}^{2}]\\ {L}_{1}\left({\boldsymbol{x}}^{\text{'}}\right)\mathrm{ }=\sum\limits _{i=1}^{n}\sum\limits _{k=1}^{c}\sum\limits _{j\in {w}_{i}}({p}_{1j}{\mu }_{ik}+{q}_{1j}-{x}_{i}^{\text{'}}{)}^{2}\end{array} $ |
s.t.
| $ \sum\limits _{k=1}^{c}{\mu }_{ik}=1 \text{,} i=\mathrm{1, 2}, \cdots , n $ |
| $ 0\le \sum\limits _{i=1}^{n}{\mu }_{ik}\le n \text{,} k=\mathrm{1, 2}, \cdots , c $ | (18) |
其中:
在此多目标模型中,
多目标函数的优化过程具体如下:
1)在KWFLICM算法中,邻域位置信息和灰度信息被引入模糊因子
2)KWFLICM算法得到的隶属度被传入像素引导隶属度滤波的目标函数
3)利用隶属度回归目标函数
| $ {\mu }_{ik}^{\text{'}}=\sum\limits _{j\in {w}_{i}}({p}_{jk}{x}_{i}+{q}_{jk})={\stackrel{-}{p}}_{ik}{x}_{i}+{\stackrel{-}{q}}_{ik} $ | (19) |
其中:
4)KWFLICM算法得到的隶属度被传入隶属度引导像素滤波的目标函数
5)像素值回归目标函数
| $ {x}_{i}^{\text{'}}=\sum\limits _{k=1}^{c}\sum\limits _{j\in {w}_{i}}({p}_{1j}{\mu }_{ik}+{q}_{1j})=\sum\limits _{k=1}^{c}{\stackrel{-}{p}}_{1i}{\mu }_{ik}+{\stackrel{-}{q}}_{1i} $ | (20) |
其中:
GFKWFLICMGF算法步骤具体如下:
1)输入原始噪声图
2)
3)根据初始化的隶属度和聚类中心,得到KWFLICM算法隶属度的更新公式
4)
5)将隶属度
6)通过新的隶属度,利用式(9)对聚类中心进行更新。
7)将新的像素值
8)当
本文算法的本质是通过引导滤波利用邻域像素值对KWFLICM算法的隶属度进行修正,同时利用像素隶属度对像素值进行引导滤波,引导滤波修正后的隶属度和像素值分别为
MRI图像的质量对临床医学的诊断有着重要意义,是由高斯噪声污染的实部图像和虚部图像经取模运算而得到的模图像,因此最终得到的图像是受莱斯噪声污染的[33]。MRI图像分布与信号有关,当图像的信噪比较大时莱斯分布趋向于高斯分布,当图像的信噪比较小时莱斯分布呈现瑞利分布,这使得去除莱斯噪声更加困难。因此,本文对受莱斯干扰的合成图、MRI图像及偏置图进行分割测试。
采用误分率(Misclassified Error,ME)、精确度(Accuracy,ACC)、峰值信噪比(Peak Signal to Noise Ratio,PSNR)、划分系数(Partition Coefficient,PC)、划分熵(Partition Entropy,PE)和Jaccard相似(Jaccard Similarity,JS)系数作为算法分割的评价指标。将像素引导隶属度滤波和隶属度引导像素滤波的交替引导滤波与KWFLICM算法相结合。为了验证本文算法的优越性,对基于交替引导滤波的核模糊聚类算法和传统核模糊聚类算法的分割结果进行比较。对合成图、MRI图像和偏置图分别添加不同强度的莱斯噪声进行测试。
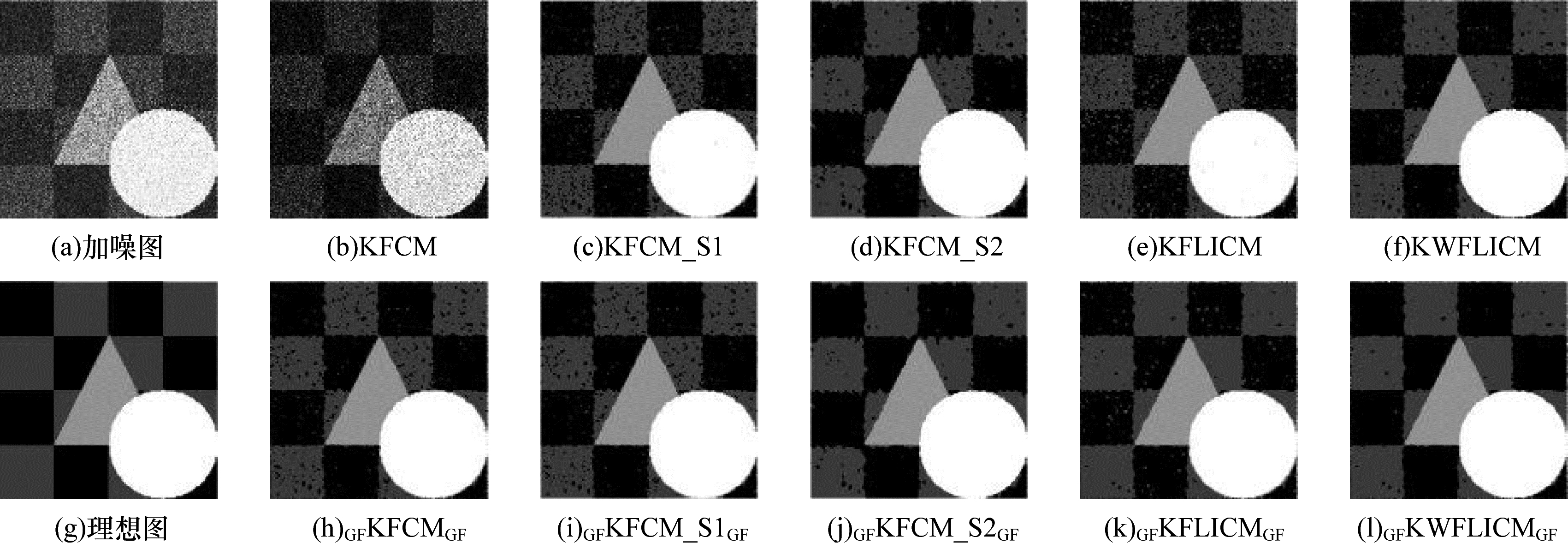
3.1 莱斯噪声干扰的合成图、MRI图、偏置图测试对合成图添加均方差为45的莱斯噪声,采用KFCM、KFCM_S1、KFCM_S2、KFLICM、KWFLICM算法及它们应用交替引导滤波进行改进的算法对图像进行分割,所得分割结果和评价指标分别如图 2及表 1所示,其中最优指标值用加粗字体标示。
|
Download:
|
| 图 2 莱斯噪声干扰的合成图及各算法分割结果 Fig. 2 Synthetic image interfered by Rician noise and segmentation results of various algorithms | |
|
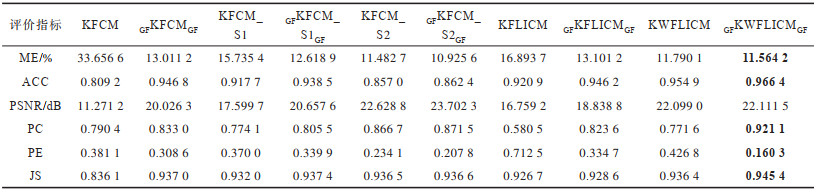
下载CSV 表 1 合成图的分割评价指标 Table 1 Segmentation evaluation indexes of synthetic image |
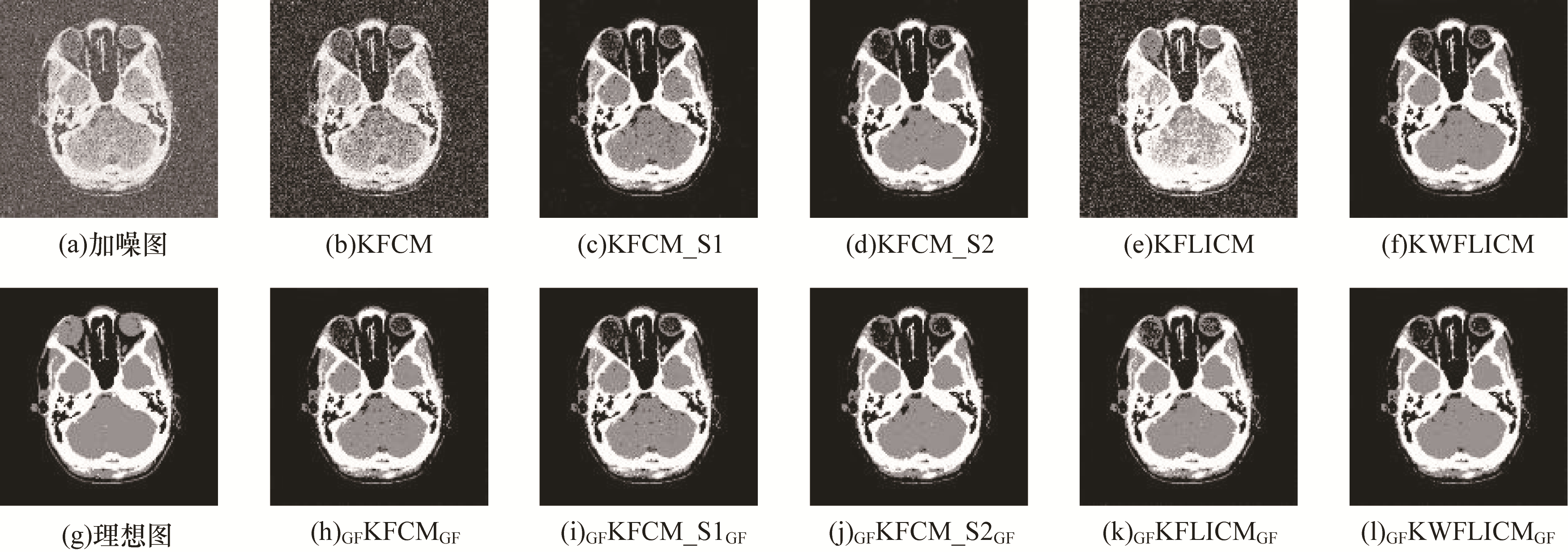
对2幅灰度MRI图像分别添加均方差为40和55的莱斯噪声,采用KFCM、KFCM_S1、KFCM_S2、KFLICM、KWFLICM算法及它们采用交替引导滤波进行改进的算法对图像进行分割,所得分割结果和评价指标分别如图 3、图 4及表 2所示,其中最优指标值用加粗字体标示。
|
Download:
|
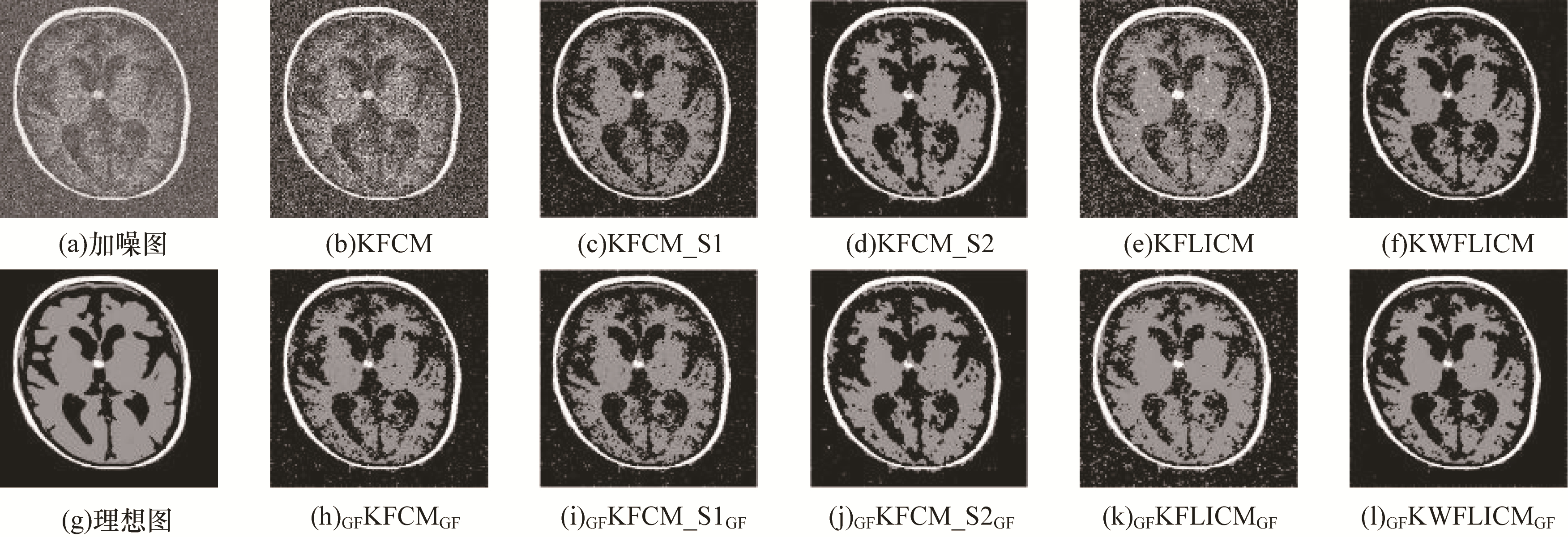
| 图 3 莱斯噪声干扰的MRI图 1及各算法分割结果 Fig. 3 MRI image 1 interfered by Rician noise and segmentation results of various algorithms | |
|
Download:
|
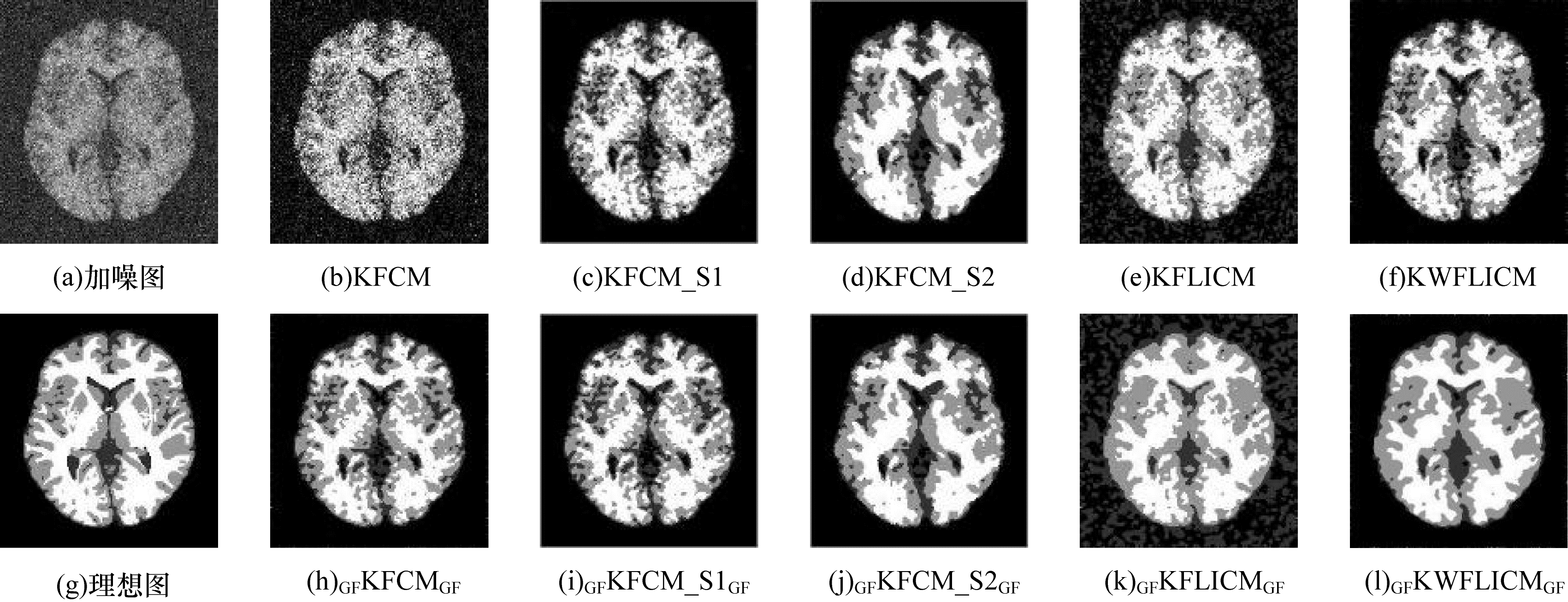
| 图 4 莱斯噪声干扰的MRI图 2及各算法分割结果 Fig. 4 MRI image 2 interfered by Rician noise and segmentation results of various algorithms | |
|
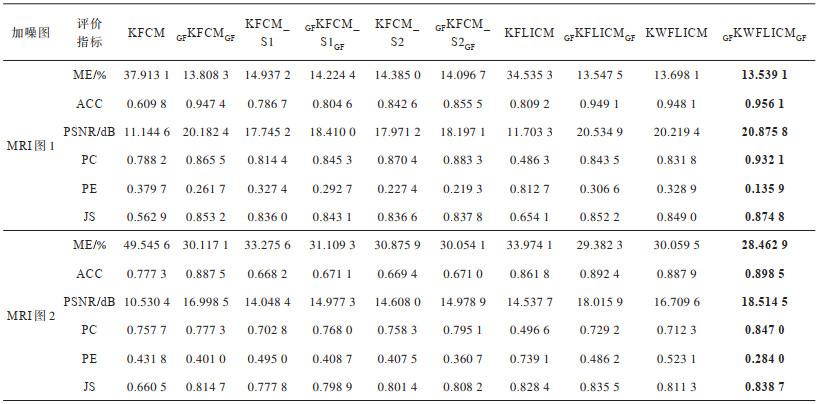
下载CSV 表 2 MRI图分割评价指标 Table 2 Segmentation evaluation indexes of MRI images |
对2幅灰度偏置图(灰度设置为20%和0%)分别添加均方差为40和40的莱斯噪声,采用KFCM、KFCM_S1、KFCM_S2、KFLICM、KWFLICM算法及它们采用交替引导滤波进行改进的算法对图像进行分割,所得分割结果和评价指标分别如图 5、图 6及表 3所示,其中最优指标值用加粗字体标示。
|
Download:
|
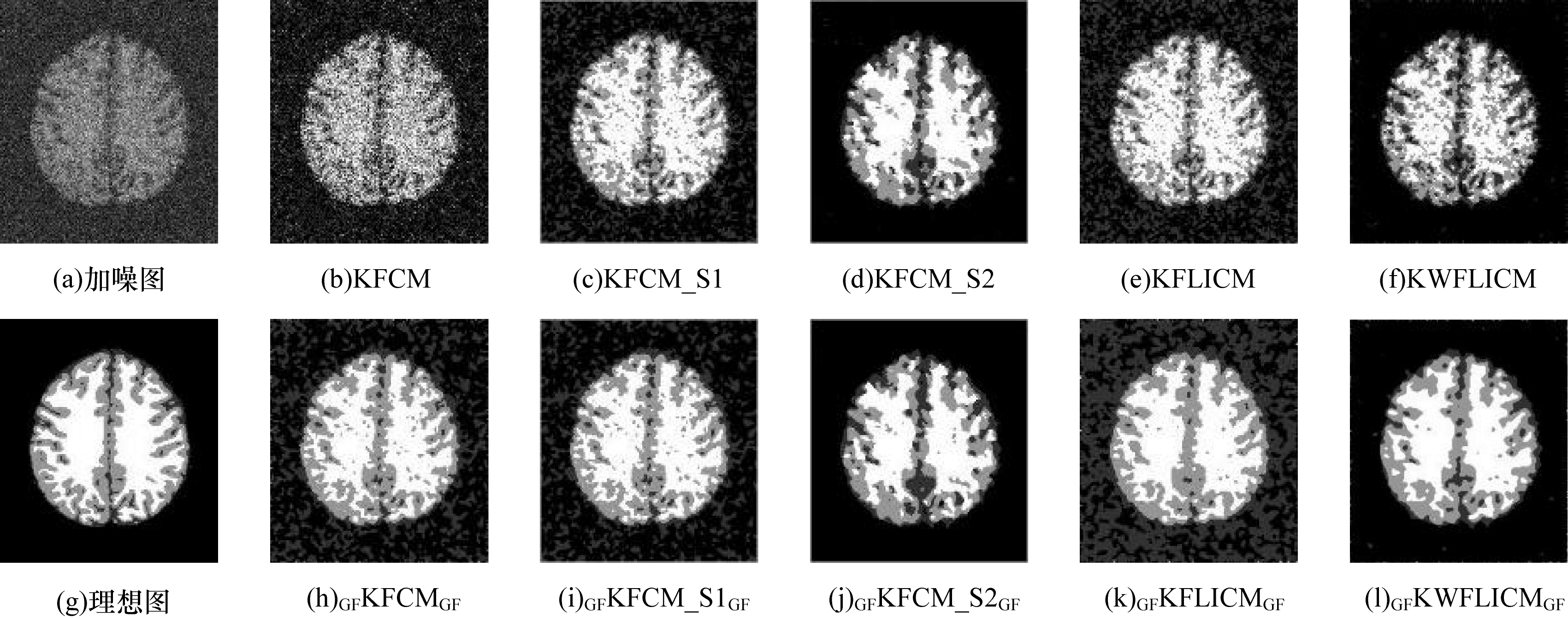
| 图 5 莱斯噪声干扰的偏置图 1及各算法分割结果 Fig. 5 Bias image 1 interfered by Rician noise and segmentation results of various algorithms | |
|
Download:
|
| 图 6 莱斯噪声干扰的偏置图 2及各算法分割结果 Fig. 6 Bias image 2 interfered by Rician noise and segmentation results of various algorithms | |
|
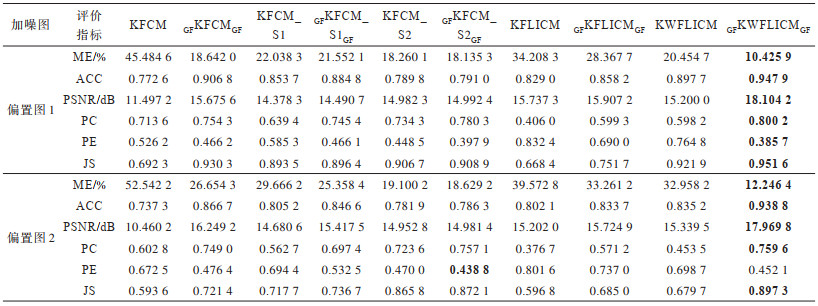
下载CSV 表 3 偏置图分割评价指标 Table 3 Segmentation evaluation indexes of bias images |
从图 2~图 6可以看出:对于受莱斯噪声干扰的图像,KFCM算法忽略了像素的空间信息,导致分割结果不理想,分割结果中含有大量噪声点;KFCM_S1、KFCM_S2、KFLICM、KWFLICM算法的分割结果中存在的噪声点较少,在一定程度上增强了算法的抗噪性、提高了算法的分割性能,其中KFCM_S2引入邻域中值信息,抑制了原图像中的大部分莱斯噪声,KFLICM算法虽然引入了具有空间邻域信息的局部模糊因子,但分割结果却不理想,KWFLICM算法在KFLICM算法的基础上改进了局部模糊因子,分割结果较好,但仍含有部分噪声,在引入交替引导滤波之后,相比于传统核模糊聚类算法,分割结果中的噪声点明显减少,算法评价指标也明显变好;将KWFLICM算法和交替引导滤波相结合的本文算法获得的图像几乎不含噪声且细节清晰,分割效果较好。
从表 1~表 3可以看出:本文算法在莱斯噪声干扰下的误分率、精确度、峰值信噪比、划分系数、划分熵、Jaccard相似系数等评价指标上表现更优,表明本文算法在莱斯噪声抑制方面具有一定的优势。
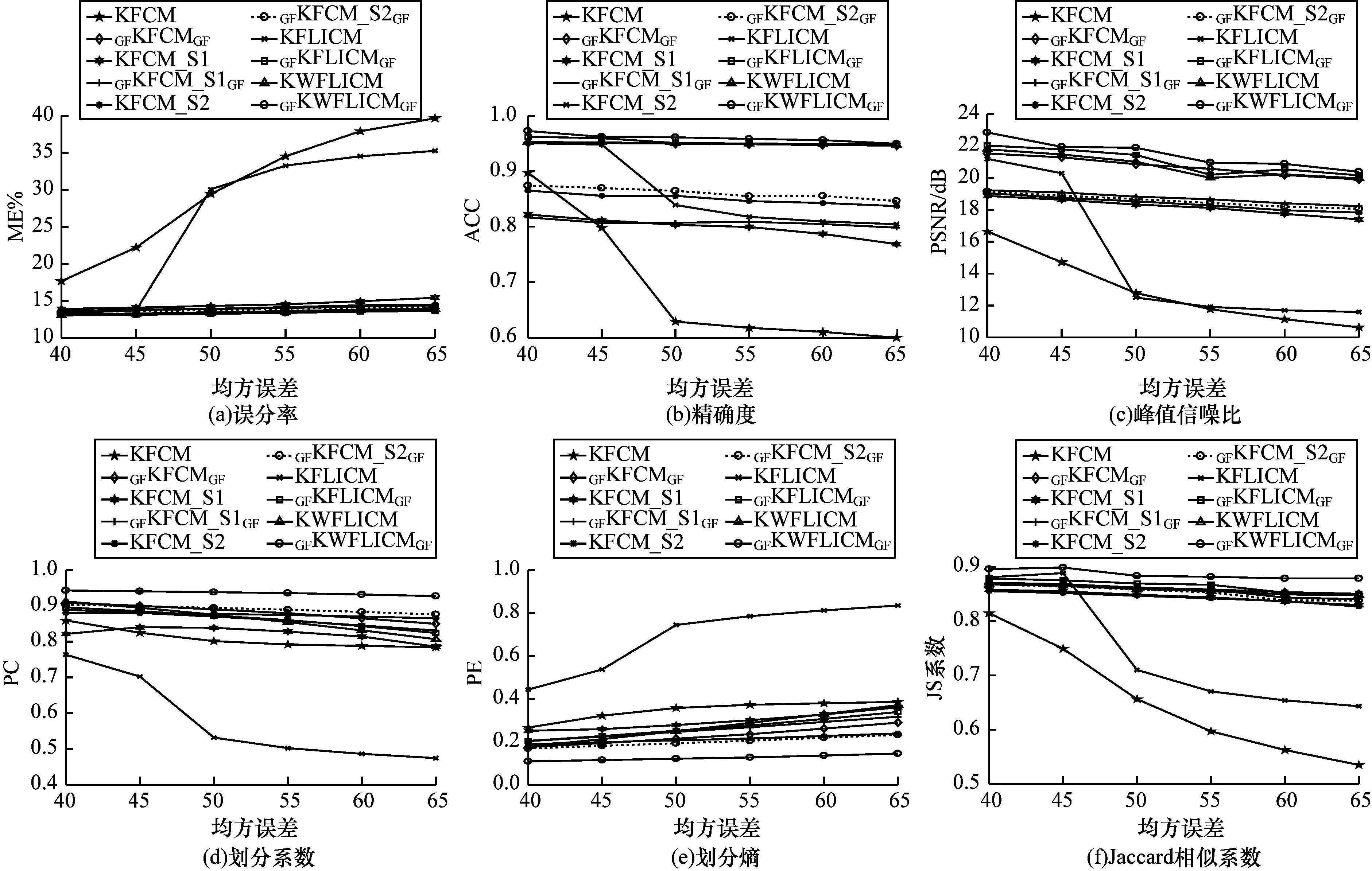
4 噪声干扰对算法性能的影响分析为了验证交替引导滤波的优越性,对MRI图 1分别添加不同强度的莱斯噪声,测试不同算法在莱斯噪声干扰下的误分率、精确度、峰值信噪比、划分系数、划分熵、Jaccard相似系数的曲线变化,如图 7所示。
|
Download:
|
| 图 7 不同算法随莱斯噪声变化的分割性能曲线 Fig. 7 Segmentation performance curves of different algorithms with Rician noise | |
从图 7可以看出,分割结果的误分率和划分熵会随着噪声强度的增加而增加,精确度、峰值信噪比、划分系数、Jaccard相似系数会随着噪声强度的增加而减小。在核空间内,基于交替引导滤波的模糊聚类算法的噪声变化曲线图均优于传统核模糊聚类算法的噪声变化曲线图。本文算法将引入空间位置信息与邻域灰度信息的KWFLICM算法与交替引导滤波相结合,随着噪声强度的增加,除个别评价指标外,其余各项评价指标均优于其他算法,且噪声变化曲线能保持相对稳定性,大幅提升了算法的性能,无论是从视觉效果还是定量评价指标来看,本文算法在抗莱斯噪声方面具有明显优势。
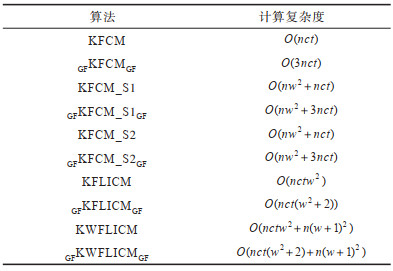
5 算法复杂度分析为比较上述算法的运行效率,对不同算法的计算复杂度进行分析。对
|
下载CSV 表 4 不同算法的计算复杂度比较 Table 4 Computational complexity comparison of different algorithms |
|
Download:
|
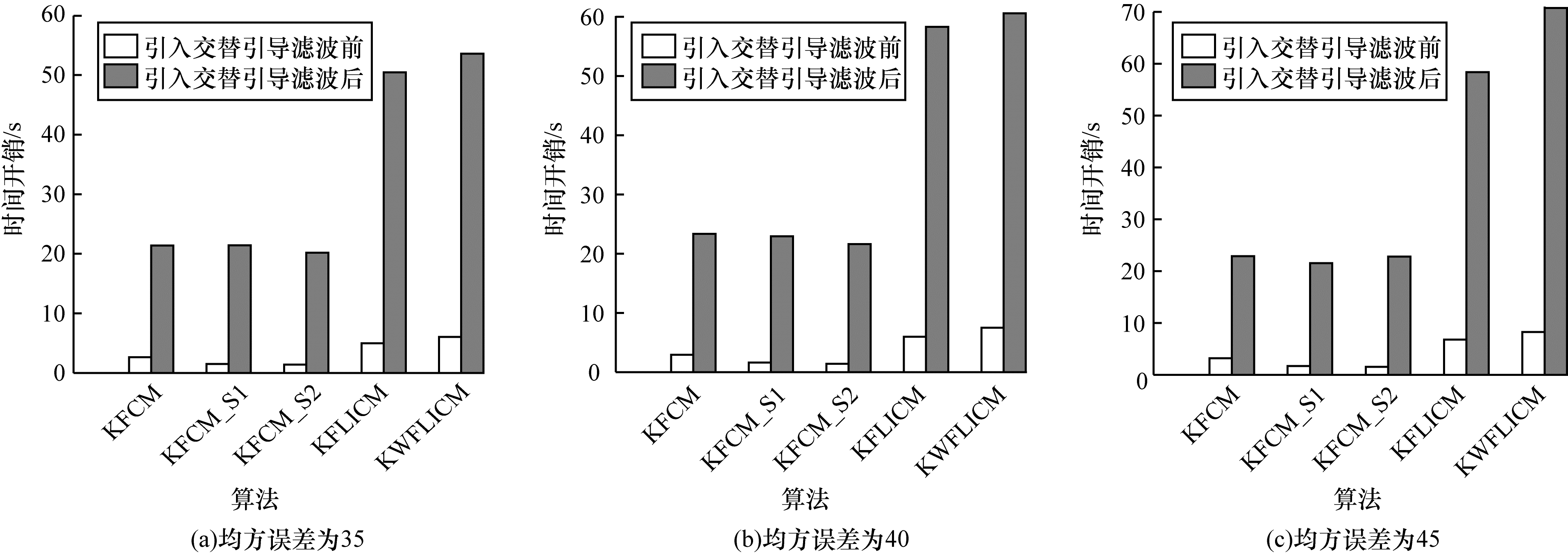
| 图 8 不同算法的时间开销比较 Fig. 8 Time cost comparison of different algorithms | |
为实现基于引导滤波的模糊聚类算法在图像分割中的应用并降低图像中噪声的敏感性,本文提出一种基于交替引导滤波的鲁棒模糊聚类算法。该算法将像素引导隶属度和隶属度引导像素的交替引导滤波与KWFLICM算法相结合,有效抑制了图像中的噪声,进一步提升了聚类性能。实验结果表明,本文算法对于莱斯噪声图像的分割效果明显优于传统核模糊聚类算法,证明了其可对噪声环境下的图像进行有效分割。后续将结合并行紧致差分进化方法、Spark平台和GPU系统进一步加快本文聚类算法的运行速度,以满足实时图像处理需求。
| [1] |
FAN X C, JU L L, WANG X Q, et al. A fuzzy edge-weighted centroidal Voronoi tessellation model for image segmentation[J]. Computers & Mathematics with Applications, 2016, 71(11): 2272-2284. |
| [2] |
张田, 田勇, 王子, 等. 基于清晰度评价的自适应阈值图像分割法[J]. 东北大学学报(自然科学版), 2020, 41(9): 1231-1238. ZHANG T, TIAN Y, WANG Z, et al. Adaptive threshold image segmentation based on definition evaluation[J]. Journal of Northeastern University(Natural Science), 2020, 41(9): 1231-1238. (in Chinese) |
| [3] |
ZHAO Q H, LI X L, LI Y, et al. A fuzzy clustering image segmentation algorithm based on hidden Markov random field models and Voronoi tessellation[J]. Pattern Recognition Letters, 2017, 85: 49-55. DOI:10.1016/j.patrec.2016.11.019 |
| [4] |
PRAHARA A, YANTO I T R, HERAWAN T. Histogram thresholding for automatic color segmentation based on k-means clustering[M]. Berlin, Germany: Springer, 2017.
|
| [5] |
刘莹, 李筠, 杨海马, 等. 结合区域生长与水平集算法的宫颈癌图像分割[J]. 电子测量与仪器学报, 2020, 34(9): 146-152. LIU Y, LI J, YANG H M, et al. Cervical cancer image segmentation based on region growth and level set algorithm[J]. Journal of Electronic Measurement and Instrumentation, 2020, 34(9): 146-152. (in Chinese) |
| [6] |
刘仲民. 基于图论的图像分割算法的研究[D]. 兰州: 兰州理工大学, 2018. LIU Z M. Research of image segmentation algorithm based on graph theory[D]. Lanzhou: Lanzhou University of Technology, 2018. (in Chinese) |
| [7] |
MEMON K H, LEE D H. Generalised kernel weighted fuzzy C-means clustering algorithm with local information[J]. Fuzzy Sets and Systems, 2018, 340: 91-108. DOI:10.1016/j.fss.2018.01.019 |
| [8] |
ESTEVES R M, HACKER T, RONG C M. Competitive K-means, a new accurate and distributed K-means algorithm for large datasets[C]//Proceedings of the 5th International Conference on Cloud Computing Technology and Science. Washington D.C., USA: IEEE Press, 2013: 17-24.
|
| [9] |
BLOCH I. Fuzzy sets for image processing and understanding[J]. Fuzzy Sets and Systems, 2015, 281: 280-291. DOI:10.1016/j.fss.2015.06.017 |
| [10] |
BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York, USA: Plenum Press, 1981.
|
| [11] |
AHMED M N, YAMANY S M, MOHAMED N, et al. A modified fuzzy C-means algorithm for bias field estimation and segmentation of MRI data[J]. IEEE Transactions on Medical Imaging, 2002, 21(3): 193-199. DOI:10.1109/42.996338 |
| [12] |
CHEN S C, ZHANG D Q. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2004, 34(4): 1907-1916. DOI:10.1109/TSMCB.2004.831165 |
| [13] |
KRINIDIS S, CHATZIS V. A robust fuzzy local information C-means clustering algorithm[J]. IEEE Transactions on Image Processing, 2010, 19(5): 1328-1337. DOI:10.1109/TIP.2010.2040763 |
| [14] |
ZHANG X F, SUN Y J, WANG G, et al. Improved fuzzy clustering algorithm with non-local information for image segmentation[J]. Multimedia Tools and Applications, 2017, 76(6): 7869-7895. DOI:10.1007/s11042-016-3399-x |
| [15] |
KANZAWA Y, ENDO Y, MIYAMOTO S. Fuzzy C-means clustering for data with tolerance using kernel functions[C]//Proceedings of IEEE International Conference on Fuzzy Systems. Washington D.C., USA: IEEE Press, 2006: 744-750.
|
| [16] |
WU Z D, XIE W X, YU J P. Fuzzy C-means clustering algorithm based on kernel method[C]//Proceedings of the 5th International Conference on Computational Intelligence and Multimedia Applications. Washington D.C., USA: IEEE Press, 2003: 49-54.
|
| [17] |
GONG M G, LIANG Y, SHI J, et al. Fuzzy C-means clustering with local information and kernel metric for image segmentation[J]. IEEE Transactions on Image Processing, 2013, 22(2): 573-584. DOI:10.1109/TIP.2012.2219547 |
| [18] |
BUADES A, COLL B, MOREL J M. A non-local algorithm for image denoising[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2005: 60-65.
|
| [19] |
HE K M, SUN J, TANG X O. Guided image filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(6): 1397-1409. DOI:10.1109/TPAMI.2012.213 |
| [20] |
OCHOTORENA C N, YAMASHITA Y. Anisotropic guided filtering[J]. IEEE Transactions on Image Processing, 2020, 29: 1397-1412. |
| [21] |
KARUMURI R, KUMARI S A. Weighted guided image filtering for image enhancement[C]//Proceedings of the 2nd International Conference on Communication and Electronics Systems. Washington D.C., USA: IEEE Press, 2017: 545-548.
|
| [22] |
GUO L, LONG C, WU Y W, et al. Image guided fuzzy C-means for image segmentation[C]//Proceedings of International Conference on Fuzzy Theory and Its Applications. Washington D.C., USA: IEEE Press, 2016: 1-6.
|
| [23] |
GUO L, CHEN L, CHEN C L P. Image guided fuzzy clustering for image segmentation[C]//Proceedings of IEEE International Conference on Systems, Man, and Cybernetics. Washington D.C., USA: IEEE Press, 2016: 4271-4276.
|
| [24] |
GUO L, CHEN L, CHEN C L P, et al. Integrating guided filter into fuzzy clustering for noisy image segmentation[J]. Digital Signal Processing, 2018, 83: 235-248. DOI:10.1016/j.dsp.2018.08.022 |
| [25] |
XU G M, ZHOU J, DONG J W, et al. Multivariate morphological reconstruction based fuzzy clustering with a weighting multi-channel guided image filter for color image segmentation[J]. International Journal of Machine Learning and Cybernetics, 2020, 11(12): 2793-2806. DOI:10.1007/s13042-020-01151-1 |
| [26] |
LEI T, JIA X H, ZHANG Y N, et al. Significantly fast and robust fuzzy C-means clustering algorithm based on morphological reconstruction and membership filtering[J]. IEEE Transactions on Fuzzy Systems, 2018, 26(5): 3027-3041. |
| [27] |
LEI T, ZHANG Y N, WANG Y, et al. A conditionally invariant mathematical morphological framework for color images[J]. Information Sciences, 2017, 387: 34-52. DOI:10.1016/j.ins.2017.01.003 |
| [28] |
LIU W, CHEN X G, SHEN C H, et al. Robust guided image filtering[EB/OL]. [2021-07-12]. https://arxiv.org/pdf/1703.09379.pdf.
|
| [29] |
SHEN X Y, ZHOU C, XU L, et al. Mutual-structure for joint filtering[C]//Proceedings of IEEE International Conference on Computer Vision. Washington D.C., USA: IEEE Press, 2015: 3406-3414.
|
| [30] |
CHUANG K S, TZENG H L, CHEN S, et al. Fuzzy C-means clustering with spatial information for image segmentation[J]. Computerized Medical Imaging and Graphics, 2006, 30(1): 9-15. |
| [31] |
ADHIKARI S K, SING J K, BASU D K, et al. Conditional spatial fuzzy C-means clustering algorithm for segmentation of MRI images[J]. Applied Soft Computing, 2015, 34: 758-769. |
| [32] |
加小红, 雷涛, 伍忠东, 等. 基于组合隶属度的快速模糊聚类算法[J]. 兰州交通大学学报, 2017, 36(1): 62-69. JIA X H, LEI T, WU Z D, et al. Fast fuzzy C-means clustering algorithm based on combined membership[J]. Journal of Lanzhou Jiaotong University, 2017, 36(1): 62-69. (in Chinese) |
| [33] |
易三莉. 基于扩散张量成像的扩散张量估算及相关技术研究[D]. 长沙: 中南大学, 2012. YI S L. Estimation of diffusion tensor and its relevant technical research based on DT-MRI[D]. Changsha: Central South University, 2012. (in Chinese) |
 2022, Vol. 48
2022, Vol. 48
