2. 智能计算及软件新技术天津市重点实验室, 天津 300384;
3. 计算机病毒防治技术国家工程实验室, 天津 300457
2. Tianjin Key Laboratory of Intelligence Computing and Novel Software Technology, Tianjin 300384, China;
3. National Engineering Laboratory for Computer Virus Prevention and Control Technology, Tianjin 300457, China
开放科学(资源服务)标志码(OSID):
比特币是一种基于P2P网络的虚拟加密数字货币[1],不依靠特定货币机构发行,根据特定算法并通过大量计算产生,使用整个P2P网络中众多节点构成的分布式账本确认并记录所有的交易行为,利用密码学设计确保货币流通各个环节的安全性。以太坊是一个开源的有智能合约功能的公共区块链平台,通过专用加密货币以太币提供去中心化的以太坊虚拟机来处理点对点合约。比特币和以太坊是区块链中最具代表性的两条公有链[2]。公有链交易以用户为基础,比特币交易发生在交易地址之间,以太坊采用账户间一对一的交易模式。
比特币相较于传统的中心化交易系统,所具有的匿名性特征能保护用户隐私不被泄露[3],但也正因为这一特性,使得比特币交易系统中产生了许多非法交易行为[4-6],例如混币服务[7-9]。混币服务是一种去中心化的隐私服务,可以使用户快速高效地与其他用户的资金进行混合,在现有账户和混币后的新账户间创建随机的映射关系并实现完全匿名[10-12]。该行为掩盖了资金来源并保护了发款人的隐私,不法分子可以通过这类资金转移方式来逃避政府监管,并可能危害公民及国家财产安全[13]。因此如何正确识别比特币交易中地址之间的关联关系,并由此推断出用户的真实身份信息已经成为比特币研究中的重要方向[14]。目前,已有一些学者对此进行了研究并取得了一定的研究成果。WU等[15]研究从比特币的公共交易历史派生的两个网络拓扑结构,并将这些结构与信息和技术相结合调查了比特币盗窃案。DUPONT等[16]演示如何收集关于比特币交易背后的真实世界的用户信息,并且通过检查用户的消费习惯来确定比特币用户的物理位置信息。PINNA等[17]通过一种基于图的方法来分析身份聚类和比特币交易中的货币流通特性,并深入了解了比特币匿名性的本质以及比特币如何在特定的用户和用户社区之间流动。ANDROULAKI等[18]对比特币的隐私问题进行评估,并提出基于多输入交易的启发式地址聚类方法。TASCA等[19]将比特币身份的最小单位(单个地址)聚合到一起,并将它们分成近似的业务实体,虽然这些实体在很大程度上可以保持匿名,但通过分析其中一些特定的交易模式,可将其中的许多实体归为特定的业务类别。
本文以公有链中的代表性应用比特币为例,提出一种基于交易网络的公有链用户识别方法。通过衡量交易地址间的相似程度将属于同一用户的交易地址进行聚合,找出属于同一用户的所有交易地址。设计一种比特币区块数据预处理方法,通过解析比特币区块数据中的脚本信息,将比特币原始交易数据处理为更加直观的格式。在实验中使用真实的比特币区块数据,通过可视化方式对用户识别结果进行分析,以验证本文方法的可行性及准确性。
1 相关工作本文通过分析比特币交易间的关联关系来实现比特币用户识别,与本文相关的工作主要有公有链地址聚类和社交网络分析[20-21]。由于比特币地址具有匿名的特征,比特币地址无法关联到用户的真实信息,这使得比特币溯源十分困难[22],因此许多研究人员对比特币地址进行了聚类分析,将属于同一实体的比特币地址聚合到一起。目前公有链地址聚类方法主要分为两类:一类是基于启发式的地址聚类;另一类是基于事务的地址聚类。ZHAO等[23]对比特币中的交易进行分析,将35 770 360个地址聚类为13 062 822个集合,并分析了聚类后的实体及其之间的联系。ZHANG等[24]从地址重用的角度重新考虑了基于一次性地址的启发式聚类方法,提出一种新的启发式地址聚类方法,通过排除那些被重用为不变地址的地址来确定一次性改变地址。CUI等[25]提出一种将IP信息与区块链交易记录相匹配的去匿名方法,并对真实的交易数据进行IP匹配实验。
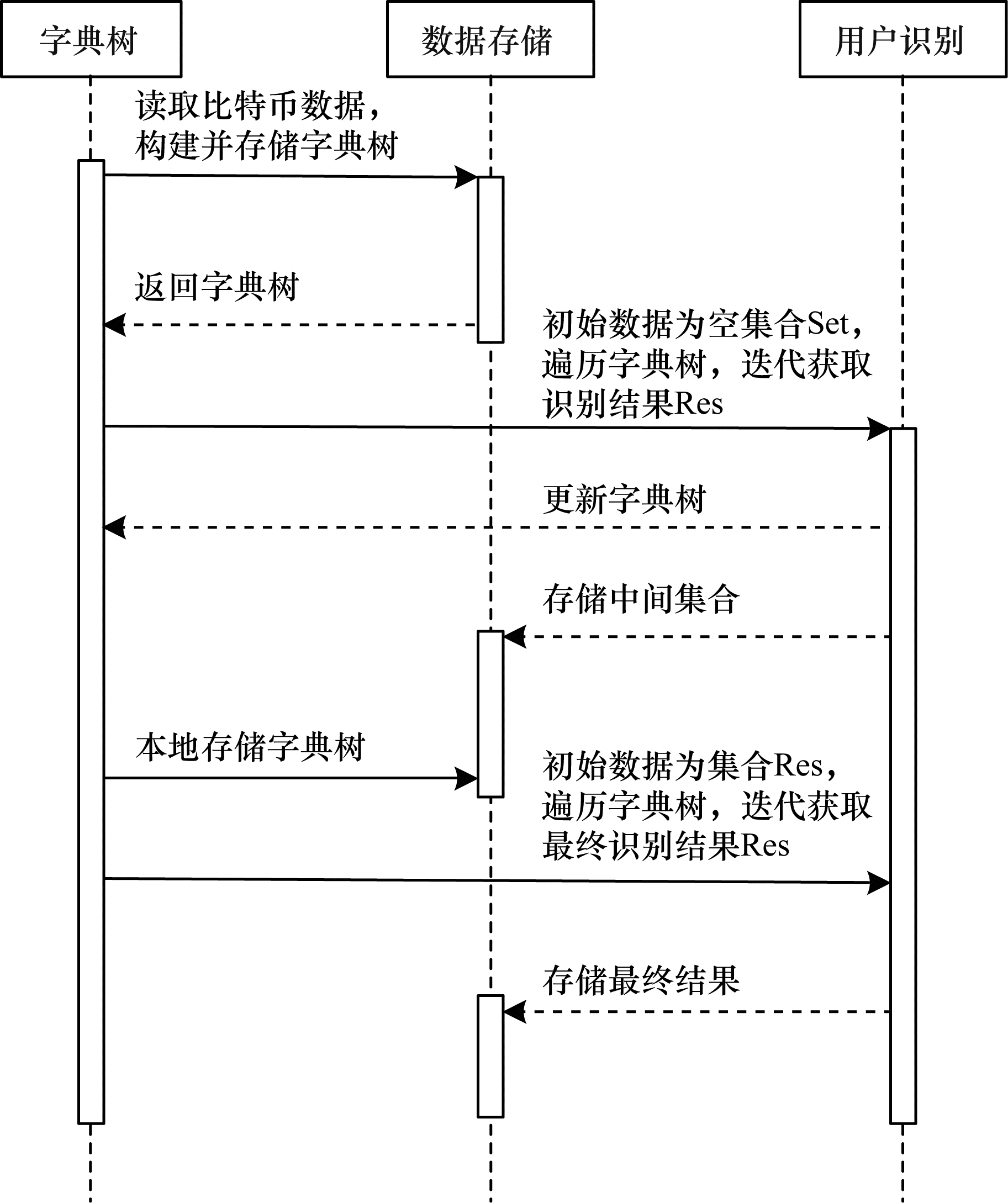
比特币交易网络本质上是一个错综复杂的社交网络[26],其中每一个比特币地址代表社交网络中的一个节点,比特币地址之间的交易代表地址之间的联系。依据社交网络分析方法,可以对比特币交易网络进行关联分析。RUFFING等[27]提出一种基于区块链的社交网络模型,该模型将用户的角色作为社交网络系统的中心。本文提出的用户识别方法在比特币地址不符合特定的地址聚类规则时,也能够通过交易网络中地址间的关联等信息对比特币用户进行有效识别。本文用户识别方法的时序图如图 1所示。
|
Download:
|
| 图 1 本文用户识别方法的时序图 Fig. 1 Sequence diagram of the proposed user identification method | |
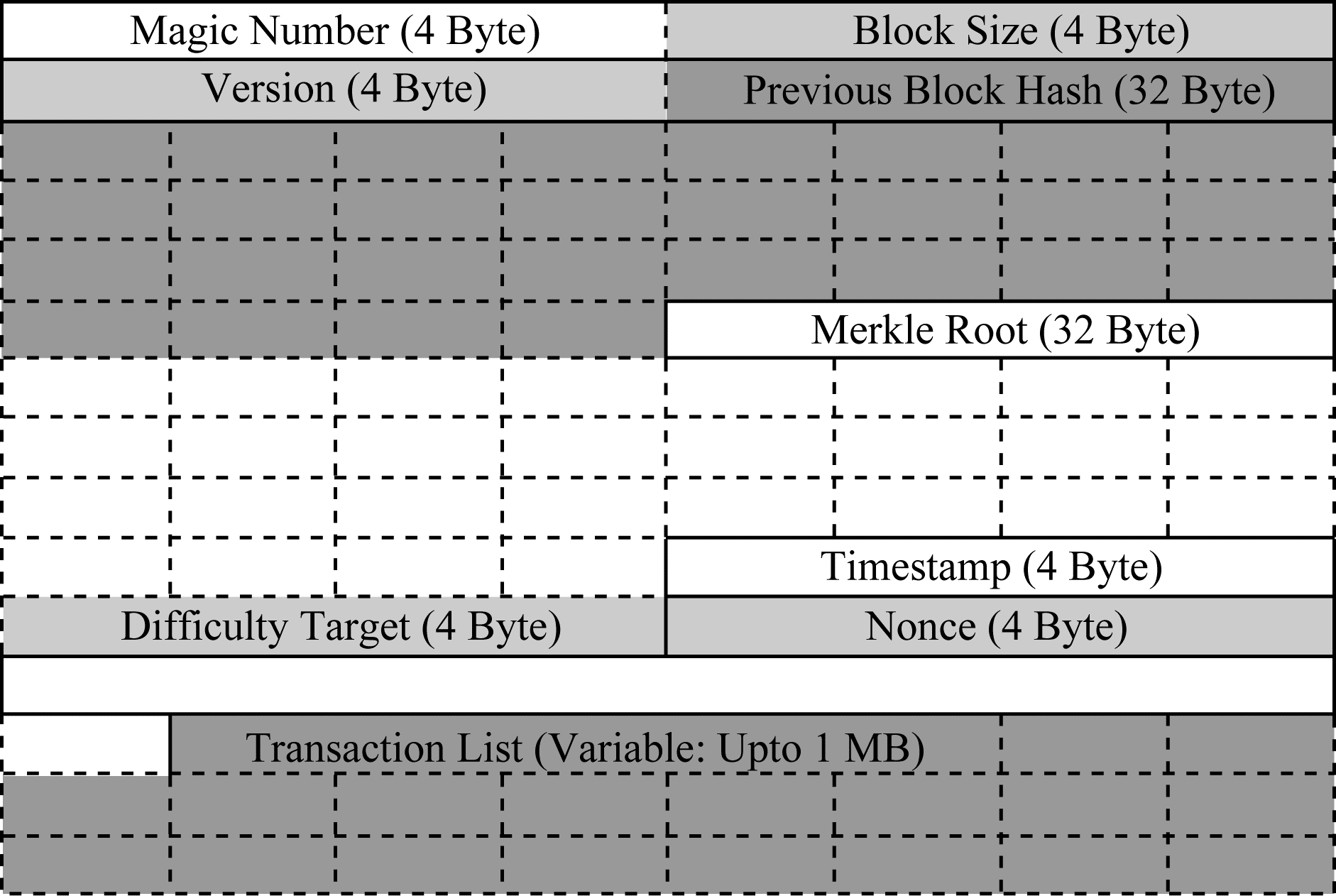
比特币实质上是一个分布式账本,该账本中的每一页对应比特币中的一个区块,比特币的区块数据中包含了比特币链上的核心信息,比特币从诞生到现在,每10分钟诞生1个区块。Dogcoin、Litecoin、DCash、ZCash等公有链中的大部分币种的底层代码均参考了比特币的底层代码[28],由比特币发展而来,因此这些币种多数与比特币具有相同的结构。区块数据结构如图 2所示。每一个数据区块记录了神奇数(Magic Number)、区块大小(Block Size)、区块头(Block Header)、交易计数(Transaction Counter)、交易详情(Transaction List)5个部分。区块头的哈希值是下一个新区块的哈希值的参考目标数,最后一项交易详情记录了该区块中所有的交易记录。区块头中记录了版本号(Version)、前一个区块的记录(Previous Block Hash)、Merkle树的根值(Merkle Root)、时间戳(Timestamp)、难度目标(Difficulty Target)和Nonce。比特币的原始数据保存方式是小端编码,也就是原始十六进制格式值需要字节逆转转化为大端数据,然后才能转化为正常的数值。大端编码是内存地址大的空间保存高位,书写出来就是左边的数据表示高位,与十进制表示法相同,更符合人们的阅读习惯。区块头数据后边紧跟的是交易信息,交易信息前面几个字节表示的是该区块包含的交易数量,coinbase交易也计入在内,其中采用可变长整型变量来表示交易数量类型。剩余的信息是普通交易信息,版本号、交易哈希值采用小端编码。输入计数器、输出计数器、解锁脚本大小和锁定交易大小均采用变长整型值。
|
Download:
|
| 图 2 区块数据结构 Fig. 2 Block data structure | |
ZHENG等[29]提出以下4种比特币地址聚类算法,结合这4种算法可以提高地址聚类效果:
1)多输入交易地址聚类算法。在一次比特币交易中,用户选择多个比特币地址作为输入地址,避免使用单一比特币地址在余额不足时产生多笔交易成本,实现了多输入交易。该交易中的所有输入地址都属于同一个实体。
2)coinbase交易地址聚类算法。比特币中每一个区块都对应一笔coinbase交易,该交易只有输出地址,没有输入地址。因此,coinbase交易中的所有输出地址都属于同一个实体。
3)找零地址聚类算法。该算法的核心是找出输出地址中的找零地址,通常来说找零地址只会在输出地址中出现一次,而不会同时出现在输入和输出地址中,输出地址也不能只包含找零地址。因此,一笔交易中的找零地址和输入地址属于同一个实体。
4)矿池地址聚类算法。如果某一笔交易中的输出地址数量超过100个,并且其中的一个地址属于一个矿池,那么这笔交易中的所有输出地址属于同一个实体。
3 比特币用户识别方法本文提出一种比特币用户识别方法,包含数据预处理、字典树构建、用户识别算法3个部分,目的是将比特币交易网络中具有强关联关系的地址映射为同一实体。
3.1 数据预处理通过配置区块链环境并搭建比特币客户端Bitcoin Core将比特币区块流数据同步到本地,同步到本地的比特币区块数据是二进制流数据,初步解析后的数据结构如下:
hash:"b96b516295b8e4f5452405db8213ca56cde630b…",
size:249,
virtual_size:168,
version:2,
lock_time:599983,
block_number:600000,
block_hash:"00000000000000000007316856900e7…",
block_timestamp:1571443461,
is_coinbase:false,
index:4,
inputs:[…],
outputs:[…],
input_count:1,
output_count:2,
input_value:0,
output_value:11695598,
fee:-11695598
比特币的交易实际上是不依赖地址的,主要依赖于脚本。在支付款项时,将支付的数额与接收者的“赎回脚本”绑定到一起。日后接收者可以用自己的“签名脚本”来确认使用权。每一笔交易的实现所依赖的只是脚本。两种常见脚本的格式具体如下:
1)支付到公钥地址模式(P2PKH):
OP_DUP OP_HASH160(0x14)[一个20字节的哈希值] OP_EQUALVERIFY OP_CHECKSIG
2)支付到脚本模式(P2SH),当使用多重签名时需要使用该模式:
OP_HASH160(0x14)[一个20字节的哈希值] OP_EQUAL
通过初步解析后的数据并不能直接看出某笔交易的输入输出地址,也不能看到交易的金额。因此,为了方便实验,针对比特币交易中的脚本格式设计了一种算法,用于解析比特币交易中的输入和输出地址以及交易涉及的金额等信息。
算法1 在交易脚本中获取交易地址
输入 比特币交易脚本
输出 比特币交易地址
1.Input script
2.for hash in script:
3.temp = SHA-256(hash)//取hash,计算其SHA-256哈希值
4.temp = SHA-256(temp)//取上一步结果,再计算其//SHA-256哈希值
5.take the first four Bytes of temp //取上一步结果的前4个//字节
6.check = hash + four Bytes //将这4个字节加在hash后//面作为校验
7.address = base58(check)//用base58表示法变换地址
8.Output address
3.2 字典树构建字典树又称单词查找树,是哈希树的变种。典型应用是用于统计、排序和保存大量字符串,经常被搜索引擎用于文本词频统计。大量的比特币地址会出现很多相同的前缀,并且在3.1节中将比特币交易数据处理成交易集合的形式,因此基于常规的字典树结构,本文提出了一种针对比特币交易数据的改进字典树结构,在字典树每个根节点之后追加一个集合,该集合用来存储与该分支表示的地址有直接交易的地址列表。
算法2 在Trie树中插入一个地址字符串
1.Insert(W):
2.P = ROOT
3.For i = 1,2,…,W.len:
4.If P.thru(W[i])== NULL://没有标识为W[i]的边
5.P.addChild(W[i],new Node())
6.P = P.thru(W[i])
7.P.markEndPoint()//标记P为终结点
8.P.addOutputList(outputList)
算法3 在Trie树中查找一个地址字符串
1.Search(S):
2.P = ROOT
3.For i = 1,2,…,S.len:
4.If P.thru(S[i])== NULL://没有标识为S[i]的边
5.Return False
6.P = P.thru(S[i])
7.Return True
3.3 用户识别算法目前,多数针对比特币地址聚类的研究是通过制定交易规则来实现地址聚类的,例如多输入交易规则、找零交易规则等。ANDROULAKI等[18]研究比特币交易中的输入地址,并设计基于多输入地址的比特币地址聚类方法,在不考虑特殊样例的情况下,基于该方法得到的聚类结果是完全正确的。MEIKLEJOHN等[30]基于找零交易规则提出一种找零地址聚类算法,该算法会将一笔交易中的输入地址和找零地址聚合为同一个实体。当部分交易中的地址符合特定的交易规则时,通过传统地址聚类算法可将这些地址聚合到一起。因此,对于符合特定交易规则的交易而言,使用这些算法能够得到很好的结果,甚至是完全正确的结果。但对于大部分的普通交易而言,这些算法往往不能取得正确的结果,因为这些交易通常没有规则可言。针对上述情况,本文通过分析比特币交易中输入与输出地址之间的关联关系,提出一种具有普适性的比特币用户识别算法。
用户识别算法的具体步骤如下:
步骤1 假设算法输入为起始节点starting_node,交易数据集合trans_network,该集合中的每一条数据代表一笔比特币交易t。设置队列Q和集合S,将起始节点starting_node分别加入到Q和S中,同时设置临时集合W和E。
步骤2 当队列Q不为空时,遍历Q中的节点,从交易数据集合trans_network中将与这些节点直接关联的节点加入到集合W中。接着遍历集合W中的节点,判断这些节点与集合S的Sim值,如果该节点的Sim值大于阈值,则将该节点分别加入集合S与集合E中,否则继续遍历。在遍历结束时,将集合E加入到队列Q中,同时将队头元素移出队列Q,并清空集合W和E。Sim值定义如下:
| $ \mathrm{S}\mathrm{i}\mathrm{m}(i, S)=\frac{{N}_{j}}{{K}_{i}}\sum\limits _{j}\left(\frac{{K}_{j}}{S}-\frac{1}{\sum {A}_{j}}\right) $ |
其中:
步骤3 重复步骤2,直到队列Q为空,此时结束循环,返回集合S。
算法4 用户识别
输入 starting_node,trans_network
输出 地址集合S
1.Queue Q = [starting_node]
2.W,E = [],[]
3.S = [starting_node]
4.while Q!= empty:
5.for vertex in Q:
6.for node in trans_network:
7.if node is related to vertex:
8.W.add(node)
9.for vertex in W:
10.if Sim(vertex,S) > threshold:
11.S.add(vertex)
12.E.add(vertex)
13.W.clear()
14.Q.push(E)
15.Q.pop()
16.E.clear()
17.return S
4 实验与结果分析选择比特币的真实交易数据作为实验数据,将其解析成改进的字典树结构,运行本文提出的用户识别算法对交易地址进行用户识别。通过可视化方式对算法执行过程进行分析并验证用户识别算法的有效性。
4.1 有效性验证在算法起始阶段,从比特币交易网络中任意选取一个节点作为起始节点,由于此时算法中的集合S为空,因此将与该节点直接关联的节点加入到网络中构成算法的初始网络。
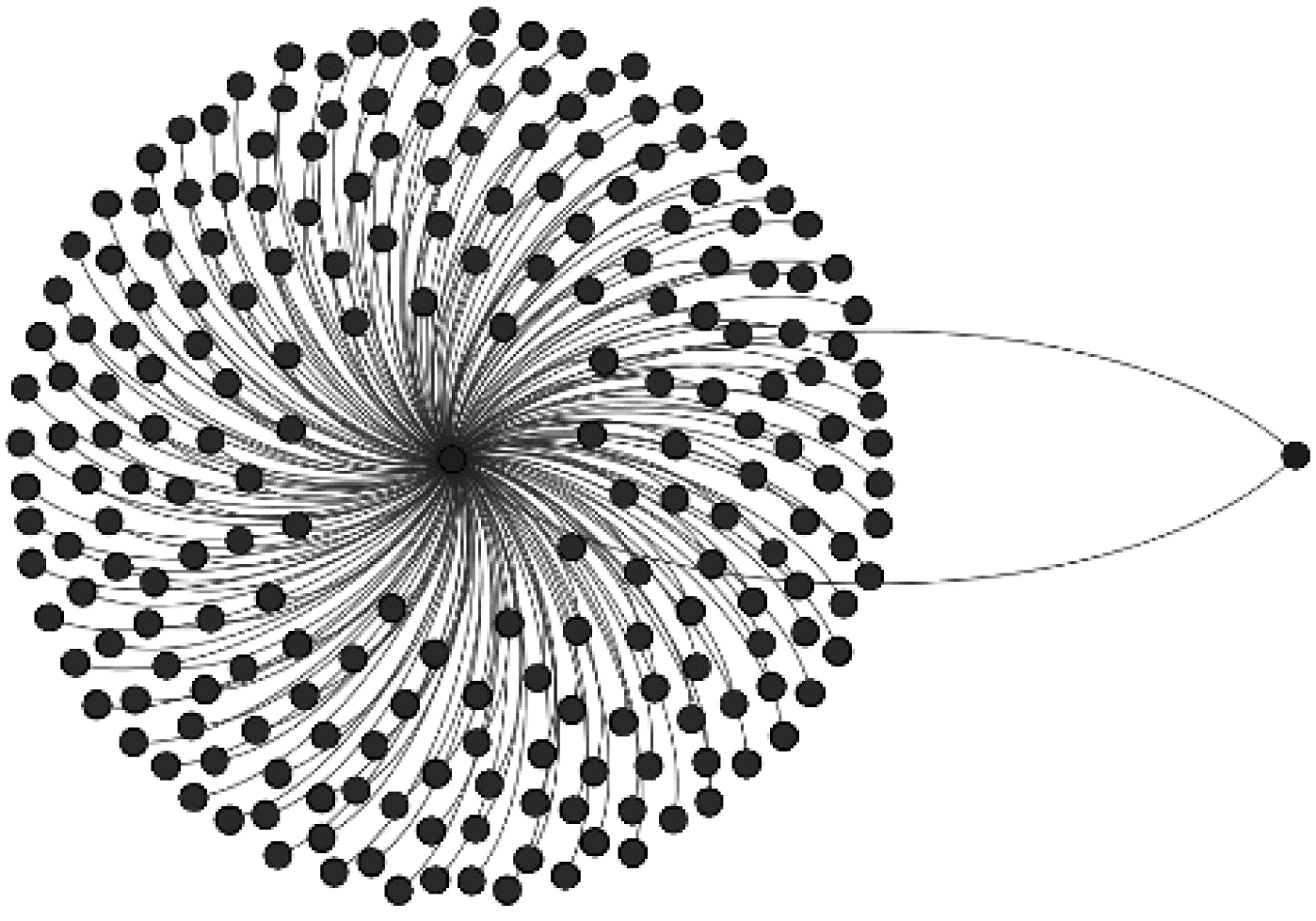
图 3为用户识别算法经一次迭代后形成的比特币交易网络。该网络中共有3类节点,其中:第1类节点出度为0、入度为1,它们只接收不发送交易;第2类节点的入度为2、出度为n,n代表第1类节点的数量,它们既发送又接收交易,同时是一个中心节点;第3类节点的入度为0、出度为2,它们只发送不接收交易。由图 3可以看出,该网络具有中心化的特性,中间的第2类节点给周围大量的第1类节点发送了交易,并且接收了来自第3类节点的交易。
|
Download:
|
| 图 3 用户识别算法经一次迭代后形成的比特币交易网络 Fig. 3 Bitcoin transaction network formed after one iteration of the user identification algorithm | |
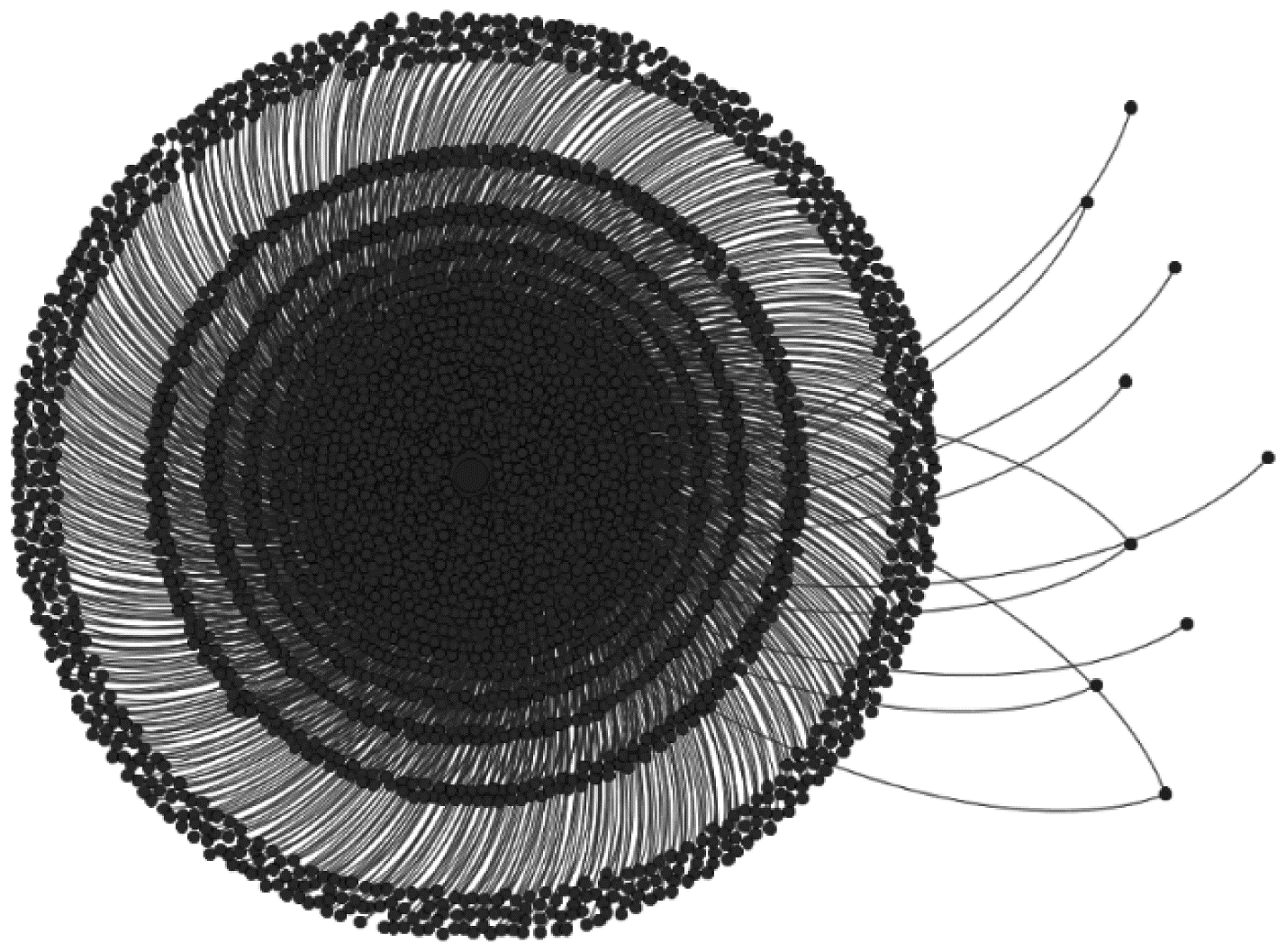
图 4为用户识别算法经多次迭代后形成的比特币交易网络。由图 4可以看出,相比于经一次迭代后形成的比特币交易网络,用户识别算法经多次迭代后有更多的节点被加入到网络中,但网络整体结构不变,仍具有中心化特性。所有节点根据出入度划分为3类节点,并且在网络中的角色也与图 3相同。
|
Download:
|
| 图 4 用户识别算法经多次迭代后形成的比特币交易网络 Fig. 4 Bitcoin transaction network formed after multiple iterations of the user identification algorithm | |
图 5为用户识别算法迭代稳定后形成的比特币交易网络,即用户识别算法迭代完成后得到的聚类结果,表示这些交易地址属于同一用户。由图 5可以看出,用户识别算法迭代稳定后形成的网络结构相比于图 3和图 4有了较大变化,网络中不只存在一个中心节点,而是有许多散布在网络边缘的“中心节点”,这些边缘的节点与中心的第1类节点群有着大量的连接,并且这些节点不同程度地复用了第1类节点,表明这些节点与第1类节点具有较强的关联性。

|
Download:
|
| 图 5 用户识别算法迭代稳定后形成的比特币交易网络 Fig. 5 Bitcoin transaction network formed after the user identification algorithm is iteratively stabilized | |
由于整个比特币交易网络数据过于庞大,因此实验部分选取比特币第140 000个至第160 000个区块间的20 000个区块作为实验数据构造交易网络,将本文提出的用户识别算法应用于该交易网络后,得到如图 6所示的比特币交易网络。

|
Download:
|
| 图 6 实验最终得到的比特币交易网络 Fig. 6 Bitcoin transaction network obtained by the experiment | |
本文提出的用户识别方法类似于关联搜索方法,借助队列进行存储,从出发点开始逐层向外查找,在查找过程中优先考虑距离出发点近的节点。无论是在邻接表还是邻接矩阵中存储,均需要借助辅助队列,且N个顶点均需入队,空间复杂度为O(N),其中N为图中的节点数。当算法开始迭代时,从一个顶点开始搜索,每个节点和每条边至少访问一次,时间复杂度为O(E),算法总时间复杂度为O(N+E),其中E为图中的边数。
地址聚类算法的评价标准通常为准确率,即算法得到的结果中正确的地址数量与总地址数量的比值,由于本文用户识别方法与传统地址聚类算法的目的相同,因此也采用准确率作为评价标准,并且使用Walletexplorer中的数据作为实验对照数据。比特币区块是连续的,如果随机选取区块链中的部分区块会导致之前区块中包含的地址间的关系无法被算法发现,为避免影响聚类结果,本文选取比特币的前160 000个区块进行实验。
图 7给出了本文用户识别方法与传统地址聚类算法的准确率对比结果。相较于传统地址聚类算法[26-27]基于规则匹配的识别方式,本文用户识别方法不受交易规则的限制,应用于特殊交易或是常规交易时均能取得稳定的结果。由图 7可以看出,随着实验涉及的区块数量的增加,传统地址聚类算法的准确率有明显的下降趋势,因为随着区块数量的增加,交易数量也不断增加,传统地址聚类算法在面对大量常规交易时,受到协议版本变化和混币服务的影响,聚类效果就会受到明显影响,从而降低准确率。本文用户识别方法不受交易规则的限制,随着区块数量的增加,准确率虽略有波动,但总体稳定在80%左右,并没有明显的下降趋势,应用于常规交易中也能取得稳定的结果。
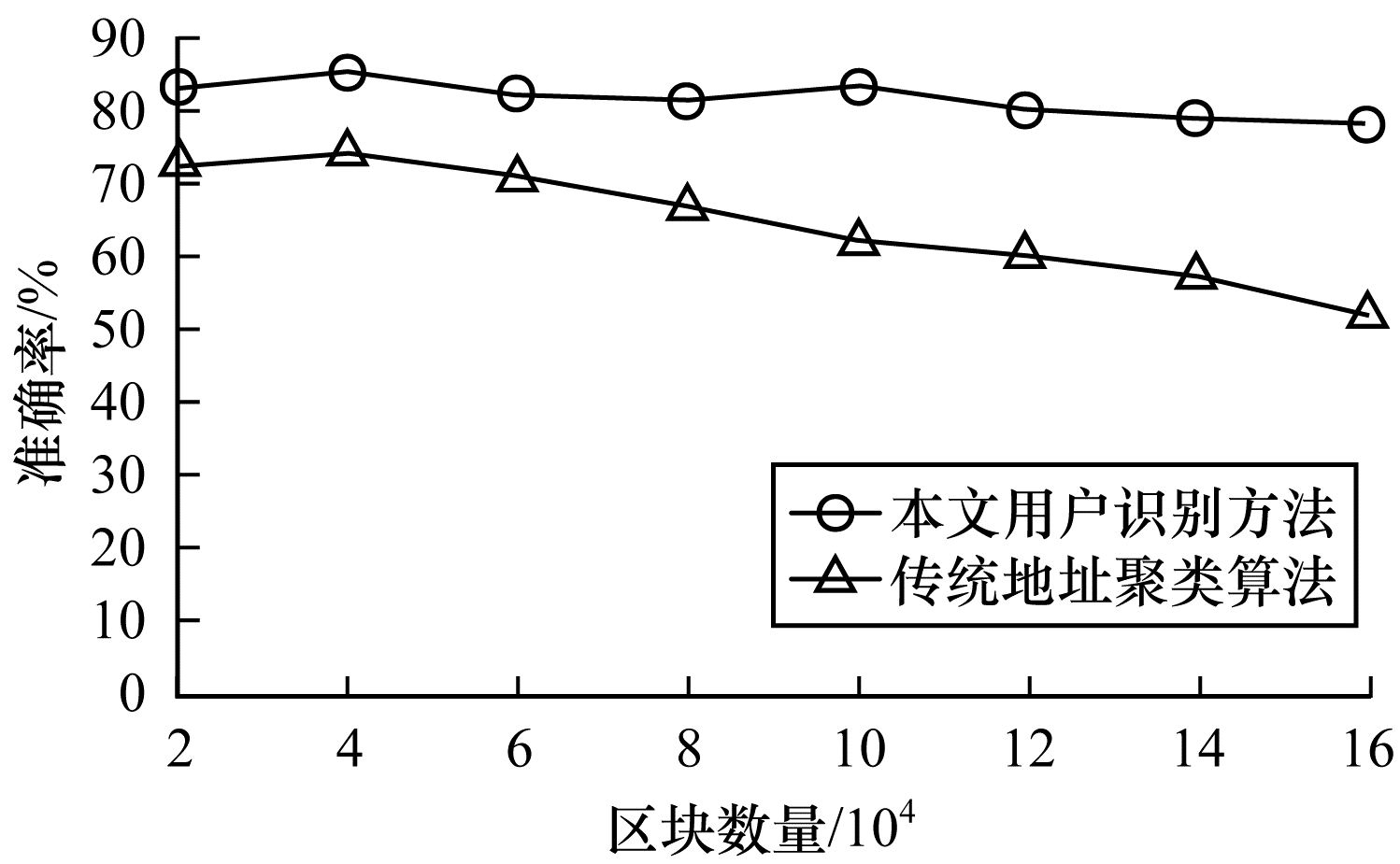
|
Download:
|
| 图 7 本文用户识别方法与传统地址聚类算法的准确率对比 Fig. 7 Comparison of the accuracy between the proposed user identification method and the traditional address clustering algorithm | |
本文在分析现有比特币用户识别方法的基础上,提出一种基于交易网络的用户识别方法,通过发现交易地址之间的关联关系,识别出属于同一用户的所有交易地址。由于公有链中大部分币种底层数据结构相同,因此本文方法不仅适用于比特币,而且对其他使用类似比特币交易模式的公有链也能取得同样的效果。实验结果表明,本文用户识别方法无论应用于常规交易还是特殊交易,均能获得相对稳定的用户识别准确率,且该结果不会受到协议版本变化和混币服务的影响而产生大幅波动。后续将继续优化用户识别方法中的核心算法,在尽量不增加算法复杂度的情况下提升用户识别准确率,同时还将在识别过程中加入用户地理位置等信息,以获得更好的识别效果。
| [1] |
Satoshi Nakamoto. Bitcoin: a peer-to-peer electronic cash system[EB/OL]. [2022-01-17]. https://bitcoin.org/en/bitcoin-paper.
|
| [2] |
邵奇峰, 金澈清, 张召, 等. 区块链技术: 架构及进展[J]. 计算机学报, 2018, 41(5): 969-988. SHAO Q F, JIN C Q, ZHANG Z, et al. Blockchain: architecture and research progress[J]. Chinese Journal of Computers, 2018, 41(5): 969-988. (in Chinese) |
| [3] |
付烁, 徐海霞, 李佩丽, 等. 数字货币的匿名性研究[J]. 计算机学报, 2019, 42(5): 1045-1062. FU S, XU H X, LI P L, et al. A survey on anonymity of digital currency[J]. Chinese Journal of Computers, 2019, 42(5): 1045-1062. (in Chinese) |
| [4] |
KHALILOV M C K, LEVI A. A survey on anonymity and privacy in Bitcoin-like digital cash systems[J]. IEEE Communications Surveys & Tutorials, 2018, 20(3): 2543-2585. |
| [5] |
CONTI M, KUMAR E S, LAL C, et al. A survey on security and privacy issues of Bitcoin[J]. IEEE Communications Surveys & Tutorials, 2018, 20(4): 3416-3452. |
| [6] |
沈蒙, 桑安琪, 祝烈煌, 等. 基于动机分析的区块链数字货币异常交易行为识别方法[J]. 计算机学报, 2021, 44(1): 193-208. SHEN M, SANG A Q, ZHU L H, et al. Abnormal transaction behavior recognition based on motivation analysis in blockchain digital currency[J]. Chinese Journal of Computers, 2021, 44(1): 193-208. (in Chinese) |
| [7] |
BIRYUKOV A, KHOVRATOVICH D, PUSTOGAROV I. Deanonymisation of clients in Bitcoin P2P network[C]//Proceedings of 2014 ACM SIGSAC Conference on Computer and Communications Security. New York, USA: ACM Press, 2014: 15-29.
|
| [8] |
ZIEGELDORF J H, MATZUTT R, HENZE M, et al. Secure and anonymous decentralized Bitcoin mixing[J]. Future Generation Computer Systems, 2018, 80: 448-466. DOI:10.1016/j.future.2016.05.018 |
| [9] |
PUTHAL D, MALIK N, MOHANTY S P, et al. Everything you wanted to know about the blockchain: its promise, components, processes, and problems[J]. IEEE Consumer Electronics Magazine, 2018, 7(4): 6-14. DOI:10.1109/MCE.2018.2816299 |
| [10] |
FEI T L, CHANG Y, WANG J Q, et al. Anonymous Bitcoin mixing scheme based on semi-trusted supervisor[C]//Proceedings of the 3rd International Conference on Electronics Technology. Washington D. C., USA: IEEE Press, 2020: 1-10.
|
| [11] |
HONG Y, KWON H, LEE J, et al. A practical de-mixing algorithm for Bitcoin mixing services[C]//Proceedings of the 2nd ACM Workshop on Blockchains, Cryptocurrencies, and Contracts. New York, USA: ACM Press, 2018: 15-20.
|
| [12] |
SEO J, PARK M, OH H, et al. Money laundering in the Bitcoin network: perspective of mixing services[C]//Proceedings of 2018 International Conference on Information and Communication Technology Convergence. Washington D. C., USA: IEEE Press, 2018: 1403-1405.
|
| [13] |
陈伟利, 郑子彬. 区块链数据分析: 现状、趋势与挑战[J]. 计算机研究与发展, 2018, 55(9): 1853-1870. CHEN W L, ZHENG Z B. Blockchain data analysis: a review of status, trends and challenges[J]. Journal of Computer Research and Development, 2018, 55(9): 1853-1870. (in Chinese) |
| [14] |
LEWENBERG Y, BACHRACH Y, SOMPOLINSKY Y, et al. Bitcoin mining pools: a cooperative game theoretic analysis[C]//Proceedings of 2015 International Conference on Autonomous Agents and Multiagent Systems. New York, USA: ACM Press, 2015: 919-927.
|
| [15] |
WU J J, LIU J L, CHEN W L, et al. Detecting mixing services via mining Bitcoin transaction network with hybrid motifs[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2022, 52(4): 2237-2249. DOI:10.1109/TSMC.2021.3049278 |
| [16] |
DUPONT J, SQUICCIARINI A C. Toward de-anonymizing Bitcoin by mapping users location[C]//Proceedings of the 5th ACM Conference on Data and Application Security and Privacy. New York, USA: ACM Press, 2015: 139-141.
|
| [17] |
PINNA A, TONELLI R, ORRÚ M, et al. A Petri nets model for blockchain analysis[J]. The Computer Journal, 2018, 61(9): 1374-1388. DOI:10.1093/comjnl/bxy001 |
| [18] |
ANDROULAKI E, KARAME G O, ROESCHLIN M, et al. Evaluating user privacy in Bitcoin[C]//Proceedings of International Conference on Financial Cryptography and Data Security. Berlin, Germany: Springer, 2013: 34-51.
|
| [19] |
TASCA P, HAYES A, LIU S. The evolution of the Bitcoin economy: extracting and analyzing the network of payment relationships[J]. The Journal of Risk Finance, 2018, 19(2): 94-126. DOI:10.1108/JRF-03-2017-0059 |
| [20] |
DORIT R, SHAMIR A. Quantitative analysis of the full Bitcoin transaction graph[C]//Proceedings of International Conference on Financial Cryptography and Data Security. Berlin, Germany: Springer, 2013: 6-24.
|
| [21] |
RUFFING T, MORENO-SANCHEZ P. ValueShuffle: mixing confidential transactions for comprehensive transaction privacy in Bitcoin[C]//Proceedings of International Conference on Financial Cryptography and Data Security. Berlin, Germany: Springer, 2017: 133-154.
|
| [22] |
LI Z T, KANG J W, YU R, et al. Consortium blockchain for secure energy trading in industrial Internet of Things[J]. IEEE Transactions on Industrial Informatics, 2017, 14(8): 3690-3700. |
| [23] |
ZHAO C, GUAN Y. A graph-based investigation of Bitcoin transaction[C]//Proceedings of IFIP International Conference on Digital Forensics. Berlin, Germany: Springer, 2015: 79-95.
|
| [24] |
ZHANG Y H, WANG J, LUO J. Heuristic-based address clustering in Bitcoin[J]. IEEE Access, 2020, 8: 210582-210591. DOI:10.1109/ACCESS.2020.3039570 |
| [25] |
CUI J M, WU H Y, FU L Y, et al. De-anonymizing Bitcoin networks: an IP matching method via heuristic approach: poster[C]//Proceedings of ACM Turing Celebration Conference. New York, USA: ACM Press, 2019: 1-2.
|
| [26] |
REMY C, RYM B, MATTHIEU L. Tracking Bitcoin users activity using community detection on a network of weak signals[C]//Proceedings of International Conference on Complex Networks and Their Applications. Berlin, Germany: Springer, 2017: 166-177.
|
| [27] |
RUFFING T, MORENO-SANCHEZ P, KATE A. CoinShuffle: practical decentralized coin mixing for Bitcoin[C]//Proceedings of European Symposium on Research in Computer Security. Berlin, Germany: Springer, 2014: 345-364.
|
| [28] |
Blockchain-etl/bitcoin-etl[EB/OL]. [2022-01-17]. https://github.com/blockchain-etl/bitcoin-etl.
|
| [29] |
ZHENG B K, ZHU L H, SHEN M, et al. Identifying the vulnerabilities of Bitcoin anonymous mechanism based on address clustering[J]. Science China Information Sciences, 2020, 63(3): 1-15. |
| [30] |
MEIKLEJOHN S, POMAROLE M, JORDAN G, et al. A fistful of Bitcoins: characterizing payments among men with no names[C]//Proceedings of 2013 Conference on Internet Measurement. Berlin, Germany: Springer, 2013: 127-140.
|
 2022, Vol. 48
2022, Vol. 48
