开放科学（资源服务）标志码（OSID）：

0 概述

聚类作为一种无监督的学习方法，广泛应用于机器学习^[1]、模式识别^[2]等技术，其通过将数据划分为多个有意义的簇从而达到分类的目的。例如，在人脸识别中，提取人脸特征后往往以特征点之间的距离为单位来衡量图像的相似度，通过聚类分析将数据分为多个簇，将相似度高的数据划分到同一簇中，从而挖掘数据之间的关系以得到正确的分类结果；在图像分割中，为了更好地区分目标与背景，可以依据图像的灰度、颜色、纹理等特征将其分割成几个区域，通过度量不同区域的灰度值将目标特征划分到同一区域，从而实现图像分割的目的。

常见的聚类方法包括K-means^[3]、层次聚类^[4]、谱聚类^[5]、子空间聚类^[6]等。K-means算法将数据点分配给最近的簇，更新每个簇的中心并重新分配所有数据点以达到聚类的效果，其性能简单且高效，但是对异常点较为敏感。谱聚类是基于图论而演化来的聚类方法，其对数据分布的适应性更强，可以识别非凸分布聚类，但是对输入的相似图十分敏感。子空间聚类是目前处理高维数据最流行的方法之一，常见的子空间聚类算法包括低秩表示（Low Rank Representation，LRR）算法^[7]、低秩子空间聚类（Low Rank Subspace Clustering，LRSC）^[8]、稀疏子空间聚类（Sparse Subspace Clustering，SSC）^[9]、核化稀疏子空间聚类（Kernel Sparse Subspace Clustering，KSSC）^[10]。其中，LRR寻找字典中最低秩的表示以更好地捕获数据结构，该方法在处理损坏数据时可以发挥关键作用；LRSC提出一个联合优化框架以求得闭合解，其能解决子空间聚类中噪声及误差的问题；SSC利用稀疏表示方法处理数据，当处理分布在多个子空间上的高维数据时，由于其自表示模型的鲁棒性而受到广泛应用；KSSC是SSC基于核技巧的拓展，使用核技巧可以得到高维空间中的稀疏表示，使得数据线性可分，从而获得更好的聚类结果。上述方法面对高维数据时取得了较好的聚类效果，但是，聚类精确性高度依赖于所学习到的相似图。因此，改变相似图学习方式能否提升聚类性能成为新的研究热点。

为了获得稳定且准确的聚类效果，NIE等^[11]提出一种自适应近邻聚类（Clustering with Adaptive Neighbors，CAN），其设计新的相似图学习方式，直接在数据空间中学习相似图，基于局部距离为每个数据自适应分配近邻，同时学习数据的相似性与聚类结构。此外，针对高维数据的处理问题，该文提出基于自适应近邻聚类的投影（Projected Clustering with Adaptive Neighbors，PCAN）方法，这种新的相似图学习方式取得了优异的效果并在实际场景中得到广泛应用。但是，该方法在学习相似图时未考虑不同特征的重要性。因此，文献[12]提出一种自动权重的自适应近邻聚类（Self-Weighted Clustering with Adaptive Neighbors，SWCAN），其对PCAN进行改进，通过对每个特征赋予相对应的权重以提升聚类性能。

上述方法均通过CAN独特的相似图学习方式获得了良好的聚类效果，然而，它们依然存在以下问题需要解决：在处理高维非线性数据时，最优核函数的选择依然存在困难；为数据分配近邻的方式考虑到了全局数据结构但未兼顾局部数据结构。

近年来，在无监督聚类任务中，随着深度学习技术的发展^[13]，自编码器的应用日益广泛。自编码器具有可压缩性，可以学习到原始数据中的重要特征，原始数据由编码层投影到潜在空间获得低维的潜在表示，再由解码层重构数据，通过最小化重构误差保留数据局部结构信息。JI等^[14]提出一种深度子空间聚类网络（Deep Subspace Clustering Network，DSC-Net），其在编码层与解码层之间加入自表示层，以模仿子空间聚类中的自表示。XIE等^[15]提出无监督深度嵌入聚类（Deep Embedded Clustering，DEC），其通过软分配方法学习数据类别，使用深度网络同时学习数据表示与聚类。LI等^[16]提出基于自编码器的自适应近邻聚类，其通过引入自编码器自适应地学习数据的非线性结构，同时更新潜在表示及相似图。文献[17]改进DSC-Net的自表达层，使之由参数化的全连接层变为一个无需参数的闭合解。上述算法利用自编码器的特性能够保留局部数据结构，但是它们认为所有特征的重要性都一致且未考虑数据的全局结构。基于以上分析，为了处理高维非线性数据同时提升聚类准确性及算法泛化能力，在聚类过程中必须兼顾全局与局部数据结构，并根据不同特征、不同重要性来对深度聚类方法进行设计与验证。

本文提出融合自动权重学习与结构化信息的深度子空间聚类（Deep Subspace Clustering Fused with Auto-Weight Learning and Structured Information，DSC-AWSI）算法。对自编码器进行预训练与微调，利用自编码器将原始数据投影到非线性潜在空间以学习数据的潜在表示，根据特征重要性的不同自适应地赋予各特征权重，从而学习相似图并完成聚类。

1 相关工作 1.1 自适应近邻聚类

假设数据矩阵$ \boldsymbol{X}=\{{x}_{1}, {x}_{2}, \cdots , {x}_{n}\}\in {\mathbb{R}}^{n\times d} $，其中，$ n $表示样本数量，$ d $表示维度。每列数据点$ {x}_{i} $的近邻可以被定义为$ k $-nearest个数据点，将欧氏距离作为距离度量单位。所有与$ {x}_{i} $相近的数据点都有一个对应的近邻概率$ {a}_{ij} $，若$ \left|\right|{x}_{i}-{x}_{j}|{|}_{2}^{2} $较小，则对应的$ {a}_{ij} $往往较大，其目标函数如下：

$ \begin{array}{l}{\mathrm{m}\mathrm{i}\mathrm{n}}\sum \limits_{j=1}^{n}\left|\right|{x}_{i}-{x}_{j}|{|}_{2}^{2}{a}_{ij}\\ {\mathrm{s}.\mathrm{t}.} \forall i, {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {\boldsymbol{a}}_{i}\le 1\end{array} $

(1)

其中：$ {\boldsymbol{a}}_{i}\in {\mathbb{R}}^{n\times 1} $是一个向量；$ {\bf{1}} $是所有元素均为1的向量。式（1）有平凡解，即当概率为1时其他数据点无法被分配为$ {x}_{i} $的近邻。为解决该问题，加入正则约束，如式（2）所示：

$ \begin{array}{l}{\mathrm{m}\mathrm{i}\mathrm{n}}\sum \limits_{i, j=1}^{n}\left|\right|{x}_{i}-{x}_{j}|{|}_{2}^{2}{a}_{ij}+\gamma {a}_{ij}^{2}\\ {\mathrm{s}.\mathrm{t}.} \forall i, {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {\boldsymbol{a}}_{i}\le 1，\mathrm{R}\mathrm{a}\mathrm{n}\mathrm{k}\left(\boldsymbol{L}\right)=n-c\end{array} $

(2)

其中：$ \gamma $为正则化参数；$ \sum \limits_{i, j}^{n}{a}_{ij}=1 $；$ \boldsymbol{L} $为拉普拉斯矩阵，$ \boldsymbol{L}={\boldsymbol{D}}_{\boldsymbol{A}}-\frac{{\boldsymbol{A}}^{\mathrm{T}}+\boldsymbol{A}}{2} $；$ \boldsymbol{A}=[{a}_{1}, {a}_{2}, \cdots , {a}_{n}]\in {\mathbb{R}}^{n\times n} $表示块对角的相似图；$ {\boldsymbol{D}}_{\boldsymbol{A}} $为相似图$ \boldsymbol{A} $的度矩阵（对角矩阵），对其添加低秩约束$ \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{k}\left(\boldsymbol{L}\right)=n-c $，$ n $为样本数量，$ c $为类别数量，为了以清晰的结构实现理想的近邻分配，连接分量必须是准确的$ c $值。对于每一个数据点$ {x}_{i} $，均可以通过式（2）为其分配近邻。为了实现理想的近邻分配使之成为自适应的分配过程，概率$ {a}_{ij}{|}_{i, j=1}^{n} $应该被施加约束，目的是无需使用K-means或其他离散方法也能使连接元素被划分为$ c $个类别。

1.2 自编码器

自编码器通过其编码器与解码器的特性，在无监督的场景下可以将原始数据非线性地投影到一个潜在空间，该过程是一种非线性降维。自编码器的作用是利用编码层将高维输入数据编码为低维数据，然后提取低维数据的显著特征^[18]，自编码器本质上可以作为特征提取器，再通过解码层解码将提取到的特征还原到初始维度，从而得到重构数据^[19]。假设神经网络具有$ m+1 $层结构，执行$ m $层非线性转化，对每个输入$ {x}_{i} $都有对应的潜在表示$ {h}_{i}^{\left(\frac{m}{2}\right)} $和重构输出$ {h}_{i}^{\left(m\right)} $，$ \boldsymbol{X}=\{{x}_{1}, {x}_{2}, \cdots , {x}_{n}\}\in {\mathbb{R}}^{n\times d} $为原始输入数据，$ {h}_{i}^{\left(0\right)}={x}_{i} $，则神经网络的计算过程为：

$ {h}_{i}^{\left(m\right)}=g({P}^{\left(m\right)}{h}_{i}^{\left(m\right)}+{b}^{\left(m\right)}) $

(3)

其中：$ g(·) $表示激活函数；$ {h}_{i}^{\left(\frac{m}{2}\right)}={z}_{i} $表示编码层潜在低维表示；$ {h}_{i}^{\left(m\right)}=\widehat{\boldsymbol{X}}\in {\mathbb{R}}^{n\times d} $表示自编码器重构的输出。

首先，将原始数据映射到潜在空间$ \boldsymbol{Z}=\{{z}_{1}, {z}_{2}, \cdots , {z}_{n}\}\in {\mathbb{R}}^{l\times n} $，其中，$ l < d $；然后，利用解码层将潜在空间的数据还原到初始维度，重构数据表示为$ \widehat{\boldsymbol{X}}=\{{\widehat{x}}_{1}, {\widehat{x}}_{2}, \cdots , {\widehat{x}}_{n}\}\in {\mathbb{R}}^{n\times d} $；最后，通过最小化重构损失$ \left|\right|\boldsymbol{X}-\widehat{\boldsymbol{X}}|{|}_{\mathrm{F}}^{2} $以保留局部数据结构。

2 模型与优化

现有很多聚类方法对大规模数据及噪声敏感，在处理高维数据时往往需要牺牲聚类质量来解决离群样本及大规模扩展问题^[20]。为此，一些优秀的特征选择方法被引入到聚类任务中^[21-22]，该类方法提取感兴趣的特征从而提升聚类效果。本文引入自编码器作为非线性数据处理方法，同时结合文献[12]中的自动权重学习思想，赋予噪声特征较低权重、有效特征较高权重，根据特征不同的重要性来为潜在空间中所学习到的特征赋予不同的权重。本文算法流程如图 1所示。

2.1 深度聚类模型

对于所有数据点$ \boldsymbol{X}=\{{x}_{1}, {x}_{2}, \cdots , {x}_{n}\}\in {\mathbb{R}}^{n\times d} $，通过自编码器的编码层将数据转换到潜在空间，得到良好的特征表示$ \boldsymbol{Z}=\{{z}_{1}, {z}_{2}, \cdots , {\mathrm{z}}_{n}\}\in {\mathbb{R}}^{l\times n} $。解码层重构数据，表示为$ \widehat{\boldsymbol{X}}=\{{\widehat{x}}_{1}, {\widehat{x}}_{2}, \cdots , {\widehat{x}}_{n}\}\in {\mathbb{R}}^{n\times d} $，则损失函数$ { \ell }_{1} $可以表示为：

$ { \ell }_{1}=\frac{1}{2}\left|\right|\boldsymbol{X}-\widehat{\boldsymbol{X}}|{|}_{\mathrm{F}}^{2} $

(4)

算法的深度神经网络中激活函数使用$ g(·) $，$ g\left(x\right)= $ $ \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(x\right)=\frac{{\mathrm{e}}^{x}-{\mathrm{e}}^{-x}}{{\mathrm{e}}^{x}+{\mathrm{e}}^{-x}} $，网络包含2层非线性转换层，即$ {g}_{1}({P}^{\left(1\right)}{x}_{i}+{b}_{1}^{\left(1\right)}) $与$ {g}_{2}({P}^{\left(2\right)}\times {g}_{1}({P}^{\left(1\right)}{x}_{i}+{b}_{1}^{\left(1\right)})+{b}_{2}^{\left(2\right)}) $，通过对神经网络施加约束来不断地优化网络参数，从而最小化重构误差。假设神经网络具有$ M+1 $层结构，执行$ M $层非线性转化，网络采用反向传播算法，需要对神经网络中涉及的参数（权重$ P $与偏执$ b $）施加约束。在正则化项中加入$ { \ell }_{1} $损失函数，如下：

$ { \ell }_{1}=\underset{{P}^{{}^{\left(m\right)}}, {b}^{\left(m\right)}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\frac{1}{2}\left|\right|\boldsymbol{X}-\widehat{\boldsymbol{X}}|{|}_{\mathrm{F}}^{2}+\frac{\delta }{2}\sum \limits_{m=1}^{M}\left(\right|\left|{P}^{\left(m\right)}\right|{|}_{\mathrm{F}}^{2}+\left|\right|{b}^{\left(m\right)}\left|{|}_{\mathrm{F}}^{2}\right) $

(5)

其中：第一项通过最小化输入与输出之间的重构误差来保留局部数据结构，相比常见的核方法，该自编码器具有更好的显式转换效果及更高的可伸缩性；第二项是正则化项，通过限制神经网络中权重与偏执的大小来避免模型过拟合。

通过编码层转换后，学习到的特征表示为$ \boldsymbol{Z}=\{{z}_{1}, {z}_{2}, \cdots , {z}_{n}\}\in {\mathbb{R}}^{l\times n} $，原始数据得到了更好的低维表征。但是，不同特征的重要性不同，在实际应用中往往没有足够的先验知识来判断各个特征的重要性。为了使模型更具鲁棒性，需要针对有效特征、噪声特征设置不同的权重，即对潜在空间的数据矩阵$ \boldsymbol{Z} $赋予不同的权重，且这种自动学习权重的方式不会改变数据的结构信息。因此，本文受文献[11-12]方法的启示，将式（2）改写为：

$ \begin{array}{c}{ \ell }_{2}=\underset{\boldsymbol{A}, \boldsymbol{W}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\sum \limits_{i=1}^{n}\sum \limits_{j=1}^{n}\left(\right||\boldsymbol{W}{z}_{i}-\boldsymbol{W}{z}_{j}|{|}_{2}^{2}{a}_{ij}+\gamma {a}_{ij}^{2})+\\ 2\mu \mathrm{T}\mathrm{r}\left({\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{F}\right)\\ {\mathrm{s}.\mathrm{t}.} \forall i, {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {a}_{ij}\le 1, \boldsymbol{F}\in {\mathbb{R}}^{n\times c}, {\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{F}={I}_{c}\end{array} $

(6)

其中：$ c $为类别数量：$ \boldsymbol{W} $表示权重矩阵，其为一个对角矩阵，每个$ {w}_{i} $值对应一个$ {z}_{i} $特征，不同的特征自适应地学习权重；$ \boldsymbol{W}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left({w}_{k}\right), 0\le {w}_{k}\le 1, k=\mathrm{1, 2}, \cdots , d $。目标函数的第一项是学习自动权重与自适应近邻的过程，根据$ \boldsymbol{W} $赋予特征$ \boldsymbol{Z} $不同的权重，再进行自适应近邻过程，学习相似图并实现聚类；第二项是低秩约束项，拉普拉斯矩阵$ \boldsymbol{L} $是半正定的^[23]，为了对$ \boldsymbol{L} $施加低秩约束，令$ {\sigma }_{i}\left(\boldsymbol{L}\right) $表示$ \boldsymbol{L} $的第i个最小特征值，$ {\sigma }_{i}\left(\boldsymbol{L}\right)\ge 0 $，根据Ky Fan’s定理^[24]中的$ \sum\limits _{i=1}^{c}{\sigma }_{i}\left(\boldsymbol{L}\right)=\underset{\boldsymbol{F}\in {\mathbb{R}}^{n\times c}, {\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{F}={I}_{c}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}Tr\left({\boldsymbol{F}}^{T}\boldsymbol{L}\boldsymbol{F}\right) $进行推导得出，其作用等同于式（2）中的$ \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{k}\left(\boldsymbol{L}\right)=n-c $。

综上，本文算法的损失函数$ { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}}={ \ell }_{1}+\lambda { \ell }_{2} $，具体计算如下：

$ \begin{array}{l}{ \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}}=\underset{{P}^{{}^{\left(m\right)}}, {b}^{\left(m\right)}, \boldsymbol{A}, \boldsymbol{W}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\frac{1}{2}\left|\right|\boldsymbol{X}-\widehat{\boldsymbol{X}}|{|}_{\mathrm{F}}^{2}+\frac{\delta }{2}\sum \limits_{m=1}^{M}\left(\right|\left|{P}^{m}\right|{|}_{\mathrm{F}}^{2}+\left|\right|{b}^{m}\left|{|}_{\mathrm{F}}^{2}\right)+\\ \lambda \left[\sum \limits_{i=1}^{n}\sum \limits_{j=1}^{n}\left(\right||\boldsymbol{W}{z}_{i}-\boldsymbol{W}{z}_{j}|{|}_{2}^{2}{a}_{ij}+\gamma {a}_{ij}^{2})+2\mu \mathrm{T}\mathrm{r}({\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{F})\right]\\ {\mathrm{s}.\mathrm{t}.} \forall i, {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {a}_{ij}\le 1, \boldsymbol{F}\in {\mathbb{R}}^{n\times c}, {\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{F}={I}_{c}\end{array} $

(7)

其中：$ \delta、\lambda $是非负权衡的参数。式（7）右侧第一项为最小化自编码器输入与输出的重构误差；第二项为正则化项，限制神经网络中的权重和偏置；第三项为聚类损失，在学习相似图$ \boldsymbol{A} $的同时根据特征重要性赋予不同的权重$ {w}_{i} $，$ \boldsymbol{A} $必须为块对角结构，$ \boldsymbol{F} $的最优解是由拉普拉斯矩阵$ \boldsymbol{L} $的$ c $个特征向量对应的最小的$ c $个特征值而构成的。通过本文模型将原始数据投影到低维潜在空间，学习到的特征表示能够兼顾全局与局部的数据结构，同时为不同的特征赋予相对应的权重，从而指导后续聚类工作。

2.2 算法优化 2.2.1 $ P, b $更新子问题

为了更清晰地表示神经网络的反向计算过程，假设神经网络具有$ M+1 $层结构，执行$ M $层非线性转化，令$ {h}_{i}^{\left(0\right)}={x}_{i}, {h}_{i}^{\left(m\right)}={\widehat{x}}_{i}, {h}_{i}^{\left(\frac{m}{2}\right)}={z}_{i}, {r}_{i}={P}^{\left(m\right)}{h}_{i}^{(m-1)}+{b}^{\left(m\right)} $，固定$ { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}} $中的其他变量，除去无关项，对$ P\mathrm{、}b $更新如下：

$ \frac{\partial { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}}}{\partial {P}^{\left(m\right)}}=({{\mathit{\Delta}} }^{\left(m\right)}+\lambda {{\mathit{\Theta}} }^{\left(m\right)})({h}_{i}^{m-1}{)}^{\mathrm{T}}+\delta {P}^{\left(m\right)} $

(8)

$ \frac{\partial { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}}}{\partial {b}^{\left(m\right)}}={{\mathit{\Delta}} }^{\left(m\right)}+ \lambda {{\mathit{\Theta}} }^{\left(m\right)}+\delta {b}^{\left(m\right)} $

(9)

$ {{\mathit{\Delta}} }^{\left(m\right)}\mathrm{、}{{\mathit{\Theta}} }^{\left(m\right)} $分别为：

$ {{\mathit{\Delta}} }^{\left(m\right)}=\left\{\begin{array}{l}-({x}_{i}-{h}_{i}^{\left(M\right)})\odot {g}^{\text{'}}\left({r}_{i}^{\left(M\right)}\right), m=M\\ ({P}^{(m+1)}{)}^{\mathrm{T}}{{\mathit{\Delta}} }^{(m+1)}\odot {g}^{\text{'}}({r}_{i}^{\left(m\right)}) , \mathrm{其}\mathrm{他}\end{array}\right. $

(10)

$ {{\mathit{\Theta}} }^{\left(m\right)=}\left\{\begin{array}{l}({P}^{(m+1)}{)}^{\mathrm{T}}{{\mathit{\Theta}} }^{(m+1)}\odot {g}^{\text{'}}({r}_{i}^{\left(m\right)}), m=\mathrm{1, 2}, \cdots , \frac{M-2}{2}\\ \sum\limits _{j=1}^{n}{a}_{ij}\left(\boldsymbol{W}{h}_{i}^{\left(\frac{M}{2}\right)}-\boldsymbol{W}{h}_{j}^{\left(\frac{M}{2}\right)}\right)\odot {g}^{\text{'}}\left({r}_{i}^{\left(\frac{M}{2}\right)}\right), m=\frac{M}{2}\\ 0, m=\frac{M+2}{2}, \cdots , M\end{array}\right. $

(11)

其中：$ {g}^{\text{'}}(·) $为激活函数$ g(·) $的导数，$ {g}^{\text{'}}\left(x\right)=\mathrm{t}\mathrm{a}\mathrm{n}{\mathrm{h}}^{\text{'}}\left(x\right)=1-\mathrm{t}\mathrm{a}\mathrm{n}{\mathrm{h}}^{2}\left(x\right) $；$ \odot $表示逐元素相乘。

在执行算法前先对所设计的神经网络进行预训练与微调，从而得到初始化的$ {P}^{\left(m\right)}\mathrm{、}{b}^{\left(m\right)} $。根据式（8）、式（9），利用随机梯度下降（Stochastic Gradient Descent，SGD）法迭代更新如下：

$ \left\{\begin{array}{l}{P}^{\left(m\right)}={P}^{{}^{\left(m\right)}}-\eta \frac{\partial { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}}}{\partial {P}^{\left(m\right)}}\\ {b}^{\left(m\right)}={b}^{\left(m\right)}-\eta \frac{\partial { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}}}{\partial {b}^{\left(m\right)}}\end{array}\right. $

(12)

其中：$ \eta $表示学习率。

2.2.2 $ \boldsymbol{W} $更新子问题

固定$ { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}} $中的其他变量，除去无关项，对$ \boldsymbol{W} $更新如下：

$ \begin{array}{l}\underset{\boldsymbol{W}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\sum \limits_{i=1}^{n}\sum \limits_{j=1}^{n}\left|\right|\boldsymbol{W}{z}_{i}-\boldsymbol{W}{z}_{j}|{|}_{2}^{2}{a}_{ij}\\ {\mathrm{s}.\mathrm{t}.} {\boldsymbol{W}}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {w}_{k}\le 1, k=\mathrm{1, 2}, \cdots , d, \boldsymbol{W}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(w\right)\end{array} $

(13)

定理1   假设$ \boldsymbol{L} $为相似图$ \boldsymbol{A} $的拉普拉斯矩阵，矩阵$ \boldsymbol{Q}\in {\mathbb{R}}^{n\times c} $的第$ i $行表示为$ {\boldsymbol{q}}_{i}^{\mathrm{T}}\in {\mathbb{R}}^{1\times c} $，则有：

$ 2\mathrm{T}\mathrm{r}\left({\boldsymbol{Q}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{Q}\right)=\sum \limits_{i, j=1}^{n}\left|\right|{\boldsymbol{q}}_{i}-{\boldsymbol{q}}_{j}|{|}_{2}^{2}{a}_{ij} $

(14)

根据定理1^[12]，假设$ {\boldsymbol{q}}_{i}=\boldsymbol{W}{z}_{i}\in {\mathbb{R}}^{d\times 1} $，即$ \boldsymbol{Q}=\boldsymbol{W}\boldsymbol{Z} $，则有：

$ \begin{array}{l}\underset{\boldsymbol{W}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\mathrm{T}\mathrm{r}\left(\boldsymbol{W}{\boldsymbol{Z}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{Z}\boldsymbol{W}\right)\\ {\mathrm{s}.\mathrm{t}.} {\boldsymbol{W}}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {w}_{k}\le 1, k=\mathrm{1, 2}, \cdots , d, \boldsymbol{W}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(w\right)\end{array} $

(15)

令$ \boldsymbol{M}={\boldsymbol{Z}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{Z}\in {\mathbb{R}}^{d\times d} $，矩阵$ \boldsymbol{M} $的第$ i $个对角元素为$ {m}_{i}^{\mathrm{*}} $，则式（13）可以转化为：

$ \begin{array}{l}\underset{\boldsymbol{W}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\mathrm{T}\mathrm{r}\left(\boldsymbol{W}\boldsymbol{M}\boldsymbol{W}\right)=\underset{{w}_{i}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\sum \limits_{i=1}^{d}{w}_{i}^{2}{m}_{i}^{\mathrm{*}}\\ {\mathrm{s}.\mathrm{t}.} {\boldsymbol{W}}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {w}_{k}\le 1, k=\mathrm{1, 2}, \cdots , d, \boldsymbol{W}=\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}\left(w\right)\end{array} $

(16)

使用拉格朗日乘子法解决式（16），先考虑约束$ 0\le {w}_{k}\le 1 $。约束$ {\boldsymbol{W}}^{\mathrm{T}}{\bf{1}}=1 $，$ 0\le {w}_{k}\le 1 $可以转换为$ {w}_{k}\ge 0 $，因为$ {m}_{i}^{\mathrm{*}}={\boldsymbol{z}}_{i}^{\mathrm{T}}\boldsymbol{L}{\boldsymbol{z}}_{i} $，$ {\boldsymbol{z}}_{i} $表示$ \boldsymbol{Z} $的第$ i $列，根据定理1，$ {m}_{i}^{\mathrm{*}} $可以转换为：

$ {\boldsymbol{z}}_{i}^{\mathrm{T}}\boldsymbol{L}{\boldsymbol{z}}_{i}=\frac{1}{2}\sum \limits_{j=1}^{n}\sum \limits_{k=1}^{n}\left|\right|{\boldsymbol{z}}_{i, j}-{\boldsymbol{z}}_{i, k}|{|}_{2}^{2}{a}_{jk} $

(17)

因为$ \boldsymbol{A} $为非负矩阵，则$ {a}_{jk}\ge 0 $，可推导出$ {m}_{i}^{\mathrm{*}}={\boldsymbol{z}}_{i}^{\mathrm{T}}\boldsymbol{L}{\boldsymbol{z}}_{i}\ge 0 $。

再考虑约束$ {\boldsymbol{W}}^{\mathrm{T}}{\bf{1}}=1 $，式（17）的拉格朗日函数可以写为：

$ \boldsymbol{L}(\boldsymbol{W}, v)={w}_{i}^{2}{m}_{i}^{\mathrm{*}}+v\left(\sum \limits_{i=1}^{d}{w}_{i}-1\right) $

(18)

对拉格朗日函数求导并令其等于0，有：

$ \frac{\partial \boldsymbol{L}(\boldsymbol{W}, v)}{\partial {w}_{i}}=2{w}_{i}{m}_{i}+v=0\Rightarrow {w}_{i}=-\frac{v}{2{m}_{i}} $

(19)

将约束$ {\boldsymbol{W}}^{\mathrm{T}}{\bf{1}}=1 $代入式（19）中，则有：

$ v=-2\frac{1}{\sum \limits_{i=1}^{d}\frac{1}{{m}_{i}^{\mathrm{*}}}} $

(20)

结合式（19）与式（20），对于$ {w}_{i} $的更新如下：

$ {w}_{i}={\left({m}_{i}^{*}\sum \limits_{i=1}^{d}\frac{1}{{m}_{i}^{\mathrm{*}}}\right)}^{-1} $

(21)

2.2.3 $ \boldsymbol{A} $更新子问题

固定$ { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}} $中的其他变量，除去无关项，假设$ {\boldsymbol{f}}_{i}^{\mathrm{T}}\in {\mathbb{R}}^{1\times c} $表示矩阵$ \boldsymbol{F}\in {\mathbb{R}}^{n\times c} $的第$ i $行，根据定理1，对$ \boldsymbol{A} $更新如下：

$ \begin{array}{l}\underset{\boldsymbol{A}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\sum \limits_{i=1}^{n}\sum \limits_{j=1}^{n}\left(\right||\boldsymbol{W}{\boldsymbol{z}}_{i}-\boldsymbol{W}{\boldsymbol{z}}_{j}|{|}_{2}^{2}{a}_{ij}+\gamma {a}_{ij}^{2})+\\ \mu \sum \limits_{i=1}^{n}\sum \limits_{j=1}^{n}\left|\right|{\boldsymbol{f}}_{i}-{\boldsymbol{f}}_{j}|{|}_{2}^{2}{a}_{ij}\\ {\mathrm{s}.\mathrm{t}.} \forall i, {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {a}_{ij}\le 1\end{array} $

(22)

由于式（22）在每个$ i $之间是独立的，因此可以对其进行简化以独立解决每个$ i $的$ \boldsymbol{A} $更新问题，如下：

$ \begin{array}{l}\underset{{a}_{i}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\sum \limits_{j=1}^{n}\left(\right||\boldsymbol{W}{\boldsymbol{z}}_{i}-\boldsymbol{W}{\boldsymbol{z}}_{j}|{|}_{2}^{2}{a}_{ij}+\gamma {a}_{ij}^{2})+\mu \sum \limits_{j=1}^{n}\left|\right|{\boldsymbol{f}}_{i}-{\boldsymbol{f}}_{j}|{|}_{2}^{2}{a}_{ij}\\ {\mathrm{s}.\mathrm{t}.} {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {a}_{ij}\le 1\end{array} $

(23)

为了更清晰地阐述算法过程，令$ {d}_{ij}^{\boldsymbol{z}}=\left|\right|{\boldsymbol{z}}_{i}-{\boldsymbol{z}}_{j}|{|}_{2}^{2}, $ $ {d}_{ij}^{\boldsymbol{f}}=\left|\right|{\boldsymbol{f}}_{i}-{\boldsymbol{f}}_{j}|{|}_{2}^{2} $，$ {d}_{ij}={d}_{ij}^{\boldsymbol{z}}+\mu {d}_{ij}^{\boldsymbol{f}} $，$ {\boldsymbol{d}}_{i}\in {\mathbb{R}}^{n\times 1} $表示$ {d}_{ij} $的第$ j $个向量，则式（23）可以改写为：

$ \begin{array}{l}\underset{{\boldsymbol{a}}_{i}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\sum \limits_{j=1}^{n}(\gamma {a}_{ij}^{2}+{d}_{ij}{a}_{ij})\Rightarrow \underset{{\boldsymbol{a}}_{i}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}{‖{\boldsymbol{a}}_{i}+\frac{1}{2\gamma }{\boldsymbol{d}}_{i}‖}_{2}^{2}\\ {\mathrm{s}.\mathrm{t}.} {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=\mathrm{1, 0}\le {a}_{ij}\le 1\end{array} $

(24)

对式（24）使用交替迭代的方法进行更新，其拉格朗日函数如下：

$ \boldsymbol{L}(a, \alpha , \beta )=\frac{1}{2}‖{\boldsymbol{a}}_{i}+\frac{1}{2\gamma }{\boldsymbol{d}}_{i}‖-\alpha ({\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}-1)-{\beta }_{i}^{\mathrm{T}}{\boldsymbol{a}}_{i} $

(25)

其中：$ \alpha、\beta \ge 0 $均为拉格朗日乘子。根据KKT条件^[25]，可推导出：

$ {a}_{ij}={\left(-\frac{{d}_{ij}^{\boldsymbol{z}}}{2{\gamma }_{i}}+\alpha \right)}_{+} $

(26)

其中：$ {(·)}_{+} $表示$ \mathrm{m}\mathrm{a}\mathrm{x}(·, 0) $。若$ {\boldsymbol{a}}_{i} $仅有$ k $个非零元素，可推出$ {a}_{ik} > 0, {a}_{i, k+1}=0 $。根据文献[11]可知，参数$ {\gamma }_{i} $的取值可以控制数据点的$ k $个近邻数量。在拥有$ k $近邻数据下，学习一个稀疏的相似图$ \boldsymbol{A} $有助于减少后续的计算成本。为了不失一般性，假设$ \forall i, {d}_{i1}^{\boldsymbol{z}}\le {d}_{i2}^{\boldsymbol{z}}\le \cdots \le {d}_{in}^{\boldsymbol{z}} $，$ {\boldsymbol{a}}_{i} $有$ k $个近邻，则有：

$ \left\{\begin{array}{l}{a}_{ik} > 0\Rightarrow -\frac{{d}_{ij}^{\boldsymbol{z}}}{2{\gamma }_{i}}+\alpha > 0\\ {a}_{i, k+1}\le 0\Rightarrow -\frac{{d}_{ij}^{\boldsymbol{z}}}{2{\gamma }_{i}}+\alpha \le 0\end{array}\right. $

(27)

根据式（26）及约束$ {\boldsymbol{a}}_{i}^{\mathrm{T}}{\bf{1}}=1 $，可得：

$ \alpha = \frac{1}{k} + \frac{1}{{2k{\gamma _i}}}\sum\limits_{j = 1}^k {d_{ij}^{\boldsymbol{z}}} $

(28)

将式（27）与式（28）相结合，可得：

$ \frac{k}{2}{d}_{ik}^{\boldsymbol{z}}-\frac{1}{2}\sum \limits_{j=1}^{k}{d}_{ij}^{\boldsymbol{z}} < {\gamma }_{i}\le \frac{k}{2}{d}_{i, k+1}^{\boldsymbol{z}}-\frac{1}{2}\sum \limits_{j=1}^{k}d_{ij}^{\boldsymbol{z}} $

(29)

为了获得具有$ k $个非零值的$ {\boldsymbol{a}}_{i} $的优化解，令：

$ {\gamma }_{i}=\frac{k}{2}{d}_{i, k+1}^{\boldsymbol{z}}-\frac{1}{2}\sum \limits_{j=1}^{k}d_{ij}^{\boldsymbol{z}} $

(30)

考虑到$ \gamma =[{\gamma }_{1}, {\gamma }_{2}, \cdots , {\gamma }_{n}] $，此处假设$ {\gamma }_{i}=\gamma $，对$ \gamma $的求解则可转化为对每个$ {\gamma }_{i} $相加求均值，如下：

$ \gamma =\frac{1}{n}\left(\frac{k}{2}{d}_{i, k+1}^{\boldsymbol{z}}-\frac{1}{2}\sum \limits_{j=1}^{k}{d}_{ij}^{\boldsymbol{z}}\right) $

(31)

根据式（26）与式（31）可推导出$ {\boldsymbol{a}}_{i} $中第$ j $个元素的闭合解为：

$ {a}_{ij}={\left(\frac{{d}_{i, k+1}-{d}_{ij}}{k{d}_{i, k+1}-\sum \limits_{j=1}^{k}{d}_{ij}}\right)}_{+} $

(32)

特别地，当$ j < k+1 $时，$ {a}_{ij} > 0 $；当$ j\ge k+1 $时，$ {a}_{ij}=0 $。

2.2.4 $ \boldsymbol{F} $更新子问题

固定$ { \ell }_{\mathrm{s}\mathrm{u}\mathrm{m}} $中的其他变量，除去无关项，$ \boldsymbol{F} $更新子问题如下：

$ \begin{array}{l}\underset{\boldsymbol{F}}{{\mathrm{m}\mathrm{i}\mathrm{n}}}\;\mathrm{T}\mathrm{r}\left({\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{L}\boldsymbol{F}\right)\\ {\mathrm{s}.\mathrm{t}.} \boldsymbol{F}\in {\mathbb{R}}^{n\times c}, {\boldsymbol{F}}^{\mathrm{T}}\boldsymbol{F}={I}_{c}\end{array} $

(33)

根据Ky Fan’s定理^[24]，最优解$ \boldsymbol{F} $由拉普拉斯矩阵$ \boldsymbol{L} $的$ c $个特征向量所对应的$ c $个最小的特征值构建。由于算法需要设计准确的$ c $值，因此最优解$ \boldsymbol{F} $可以直接用于聚类任务，无需K-means或者其他离散方法。

基于上述分析，本文DSC-AWSI算法描述具体如算法1所示。

算法1 DSC-AWSI算法

输入  原始数据$ \boldsymbol{X} $，参数$ c $，$ k $，$ \delta $，$ \lambda $，$ \gamma $，模型层数$ M $

输出 特征权重$ \boldsymbol{W} $，聚类结果$ Y $，神经网络参数$ \{{P}^{\left(m\right)}, {b}^{\left(m\right)}{\}}_{m=1}^{M} $

初始化 神经网络$ \{{P}^{\left(m\right)}, {b}^{\left(m\right)}{\}}_{m=1}^{M} $，特征权重$ \boldsymbol{W} $，相似图$ \boldsymbol{A} $

For m=1，2，…，M

根据正向传播计算得到$ \{{\mathrm{h}}_{\mathrm{i}}^{\left(\mathrm{m}\right)}{\}}_{\mathrm{m}=1}^{\mathrm{M}} $

While not converge do

1.For i=1，2，…，n

2.获得初始化表示$ {\mathrm{h}}_{\mathrm{i}}^{\left(0\right)}={\mathrm{x}}_{\mathrm{i}} $

3.经过编码层训练计算潜在表示$ {\mathrm{h}}_{\mathrm{i}}^{\left(\frac{\mathrm{M}}{2}\right)}={\mathrm{z}}_{\mathrm{i}} $

4.将得到的潜在表示$ {\mathrm{z}}_{\mathrm{i}} $输入到目标函数式（7）中

5.通过式（34）更新拉普拉斯矩阵$ \mathrm{F} $

6.通过式（22）更新权重$ \mathrm{W} $

7.通过式（33）更新相似图$ \mathrm{A} $

8.For m=1，2，…，M

9.通过式（8）、式（9）、式（12）更新$ \{{\mathrm{P}}^{\left(\mathrm{m}\right)}, {\mathrm{b}}^{\left(\mathrm{m}\right)}{\}}_{\mathrm{m}=1}^{\mathrm{M}} $

10.End

11.通过式（3）计算$ \{{\mathrm{h}}_{\mathrm{i}}^{\left(\mathrm{m}\right)}{\}}_{\mathrm{m}=1}^{\mathrm{M}} $

12.End

13.由相似图$ \mathrm{A} $学习聚类结果$ \mathrm{Y} $

14.返回聚类结果$ \mathrm{Y} $和神经网络参数$ \{{\mathrm{P}}^{\left(\mathrm{m}\right)}, {\mathrm{b}}^{\left(\mathrm{m}\right)}{\}}_{\mathrm{m}=1}^{\mathrm{M}} $

2.3 复杂度分析

本文所提模型设定的隐藏层数$ M=2 $，模型包含神经网络反向传播训练及聚类过程，聚类优化过程分为3个子问题，$ \boldsymbol{A} $更新子问题的复杂度为$ O(n{d}^{2}+{n}^{2}d) $，$ \boldsymbol{F} $更新子问题的复杂度为$ O\left({n}^{3}\right) $，$ \boldsymbol{W} $更新子问题的复杂度为$ O\left({n}^{2}d\right) $，聚类过程的总复杂度为$ O({n}^{3}+nd\mathrm{m}\mathrm{a}\mathrm{x}(n, d\left)\right) $。假设自编码器中隐藏层的维度最大值为$ D $，则算法的总复杂度为$ O({n}^{3}+nd\mathrm{m}\mathrm{a}\mathrm{x}(n, d)+n{D}^{2}) $。

3 实验结果与分析 3.1 实验设置

为了验证本文算法的有效性，使用较为常见的几种聚类算法在多种数据集上进行实验测试，并选取10次实验的平均值作为结果。实验环境为AMD Ryzen 2600X处理器、16 GB RAM、显卡配置GeForce GTX 1660ti，在Windows 10系统上进行实验。

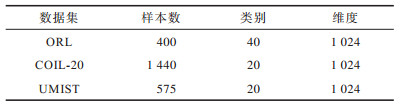
在ORL、COIL-20、UMIST这3个数据集上进行实验测试：

1）ORL数据集中包含40个人在不同的光照、时间和表情下的400幅面部图像。

2）COIL-20数据集包含20个物体在不同旋转角度下的图像，每个物体有72幅图像。

3）UMIST数据集包含20个人的575幅图像，每个人具有不同角度、不同姿态的多幅图像。

上述数据集中的图像都为32×32像素，数据集具体描述如表 1所示。

在实验过程中，自编码器的隐藏层数$ M=2 $，隐藏层维度设置为400维-200维-400维（以下简写为400-200-400），类别数目$ c $根据数据集设置不同值，近邻数目$ k $在（2，50）区间内取值，从而观察不同$ k $值下算法的聚类性能（由于$ k $为近邻数目，值为0或1均不合理）。设置$ \gamma =-1 $，$ \mu $为拉普拉斯矩阵约束参数，为了加速收敛过程，令$ \mu =\gamma $，在每次迭代中，若相似图$ \boldsymbol{A} $的连通分量远小于$ c $，则增大$ \mu $，反之则减小$ \mu $。学习率$ \eta $设置为$ \eta ={2}^{-12} $，$ \delta $设置为固定值$ {10}^{-3} $，根据不同数据集，参数$ \lambda $从$ \left\{5\times {10}^{-4}, {10}^{-3}, 5\times {10}^{-3}, {10}^{-2}, 5\times {10}^{-2}, {10}^{-1}\right\} $中选出最优值。此外，当网络的均方误差损失最小值小于$ {10}^{-3} $或迭代次数达到400时，则默认算法收敛。

3.2 结果分析

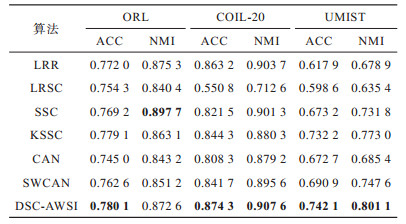
将本文算法与6种常见的聚类算法在上述数据集上进行实验，对比算法包括LRR^[7]、LRSC^[8]、SSC^[9]、KSSC^[10]、CAN^[11]、SWCAN^[12]。上述6种算法均由原作者提供的代码进行实验，为确保公平性，算法具体参数根据原论文设置为最优，在最优参数下进行结果对比。使用常见的聚类指标ACC（Accuracy）、NMI（Normal Mutual Information）来衡量算法的聚类性能，实验结果如表 2所示，最优结果加粗表示。

从表 2可以看出，相比子空间聚类算法及自适应近邻聚类算法，本文算法在公开数据集上可以得出更好的聚类效果：在COIL-20数据集上本文算法的ACC相比CAN、SWCAN算法提高了6.6和3.23个百分点；在ORL数据集上本文算法的ACC相比CAN、SWCAN算法提高了3.51和1.75个百分点；在UMIST数据集上本文算法的ACC、NMI值相比CAN、SWCAN平均提高了6.94和5.12个百分点，这说明引入自编码器可以在特征选择时更好地保持局部数据结构，验证了深度网络处理高维非线性数据的有效性，同时也体现出自动权重学习通过赋予特征权重的方式能够解决噪声数据问题，使得邻接矩阵能够取得更好的学习效果。但是，本文算法的NMI值与SWCAN算法相差较小，原因可能是两者的子空间相似图学习方式相同。在ORL数据集上，本文算法的NMI值低于SSC算法，原因可能是本文算法没有使用数据自表示以及对相似图的分割没有使用谱聚类，这说明了数据自表示方法有利于加强相同簇内数据点之间的联系。

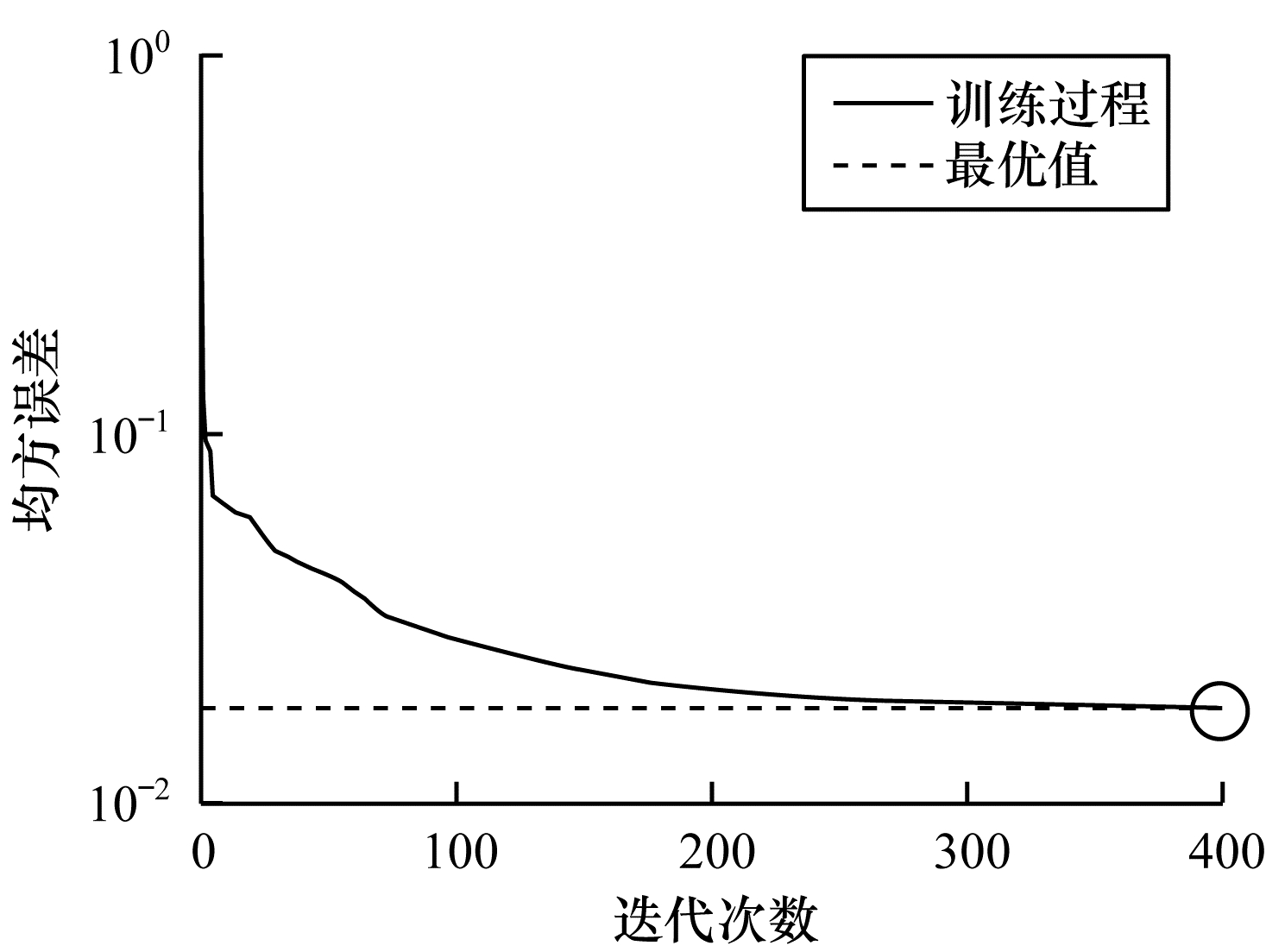
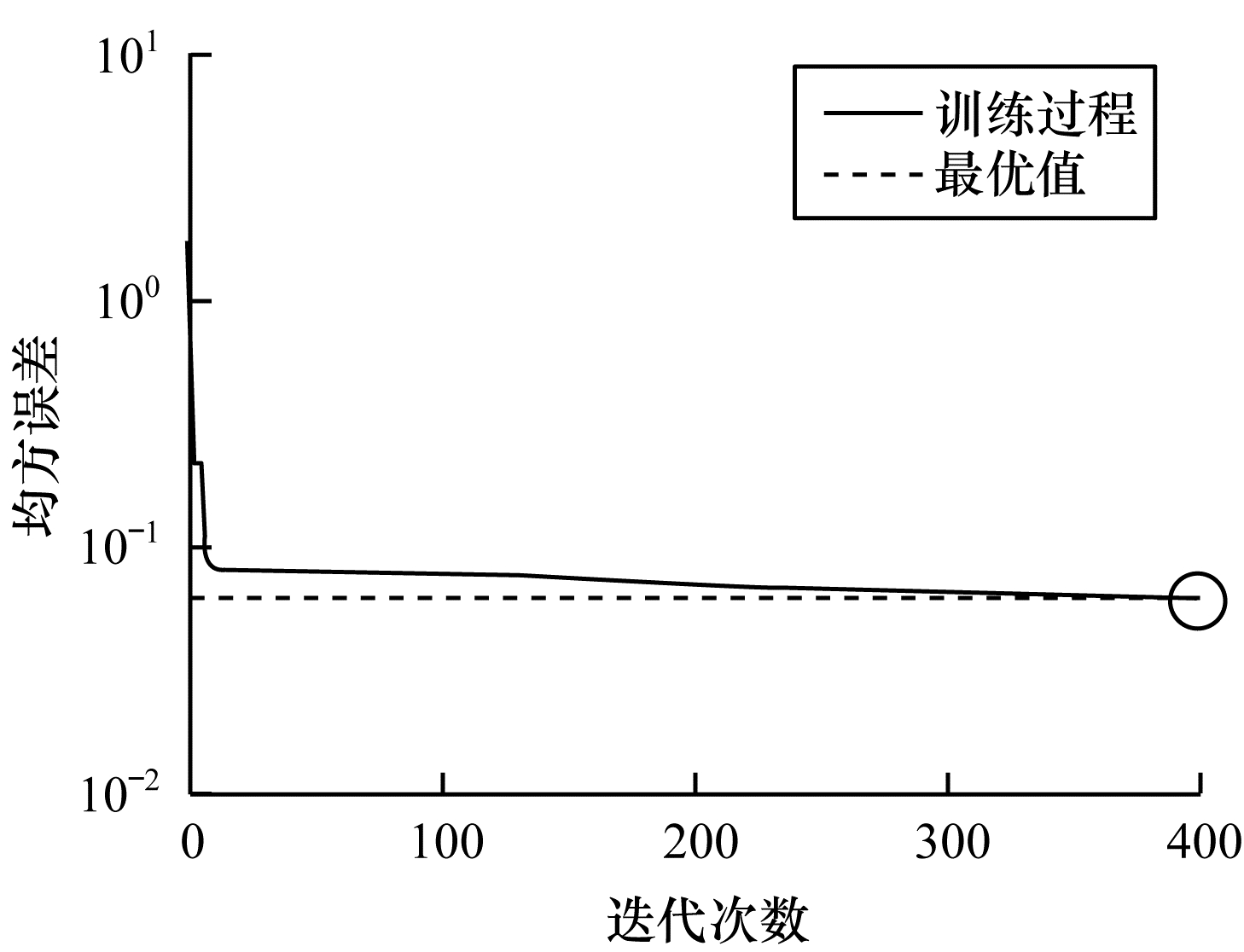
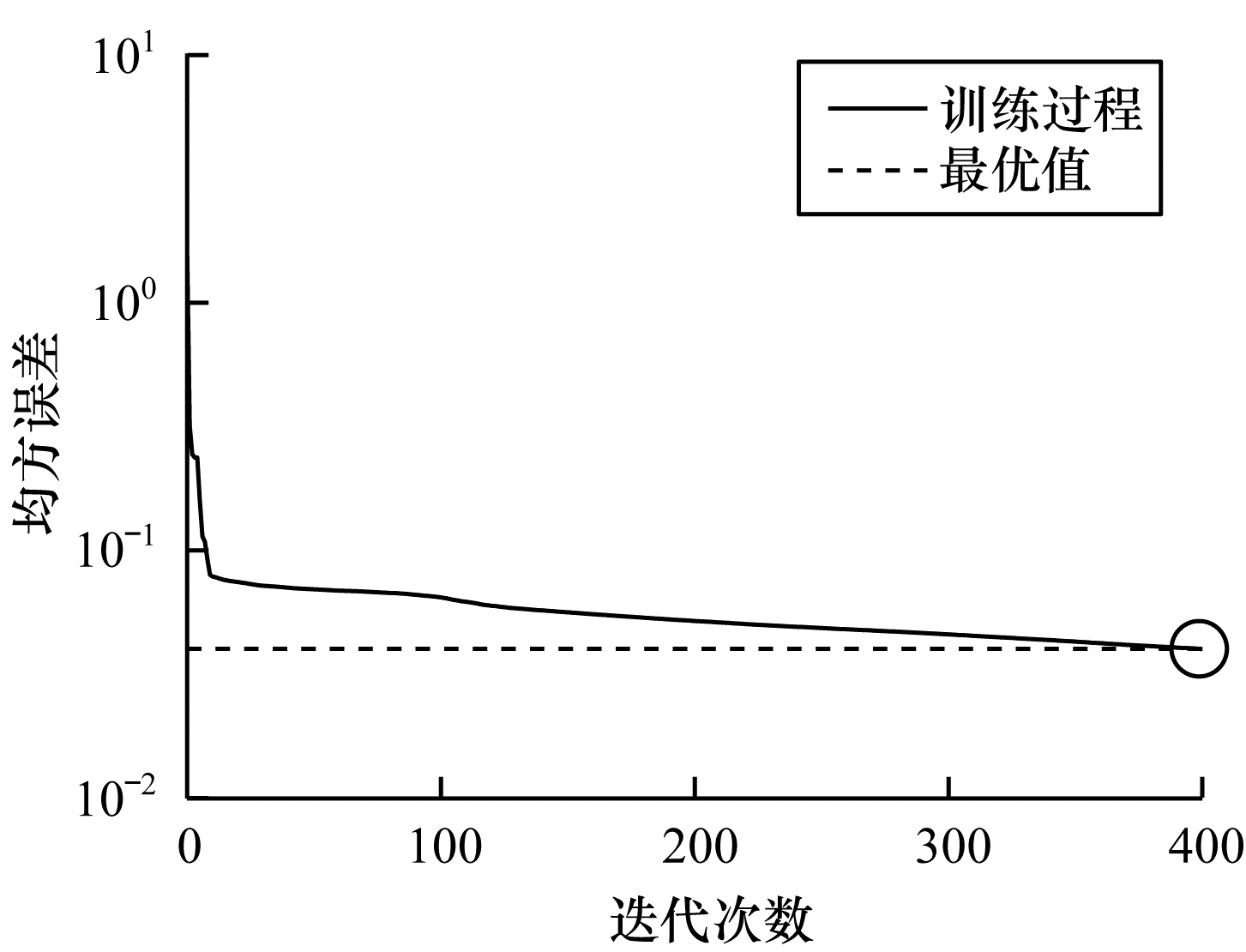
图 2~图 4分别表示在不同数据集上根据迭代次数增加的神经网络训练的重构损失变化。从中可以看出，在迭代400次以后，COIL-20数据集上的均方误差最低达到0.017 88，ORL数据集上的均方误差最低达到0.060 34，UMIST数据集上的均方误差最低达到0.039 986，即随着迭代次数的增加，通过深度网络训练的重构误差逐渐减小，表明在影响（误差）较小的情况下能够通过深度网络保留数据局部结构。

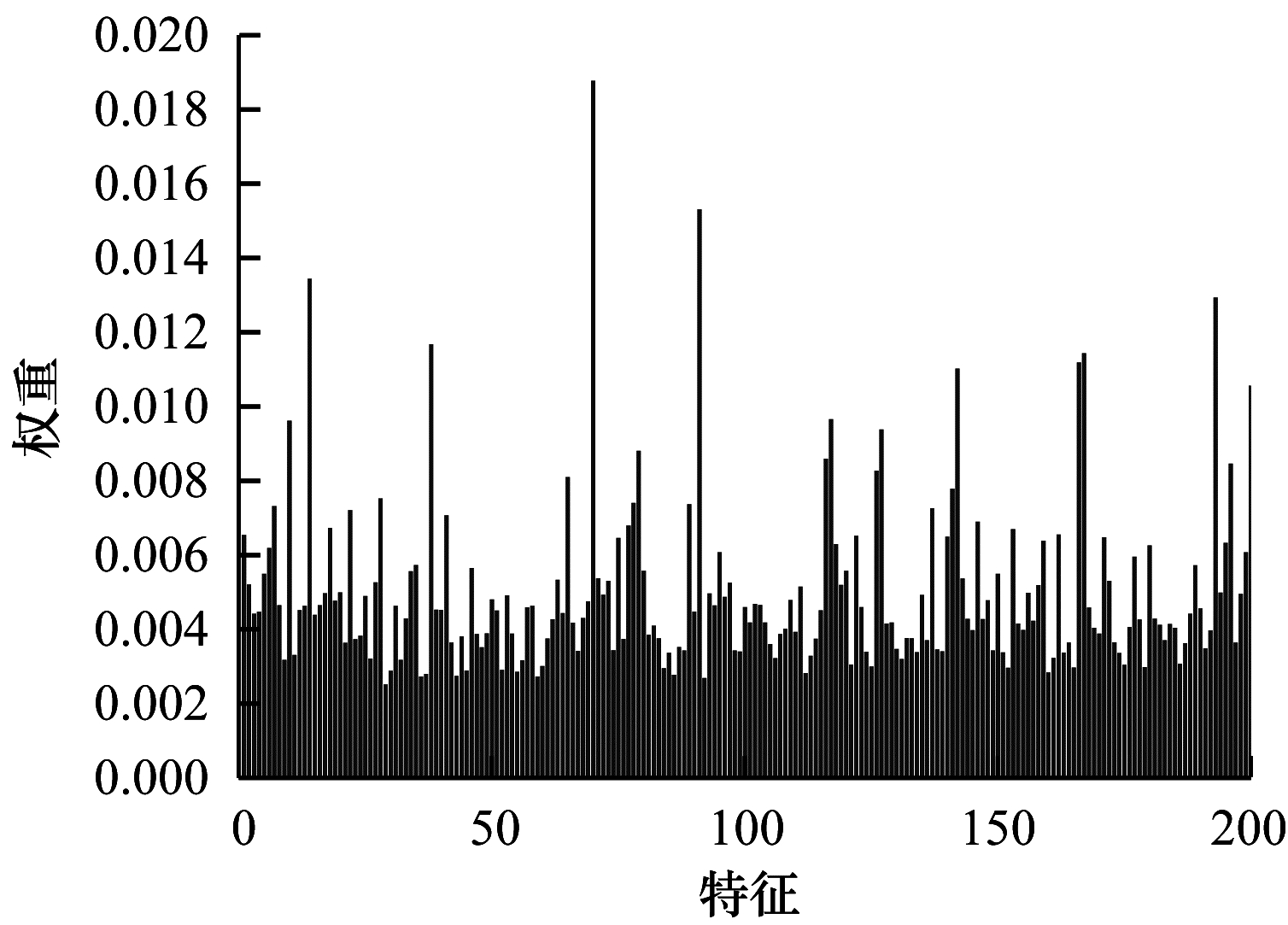
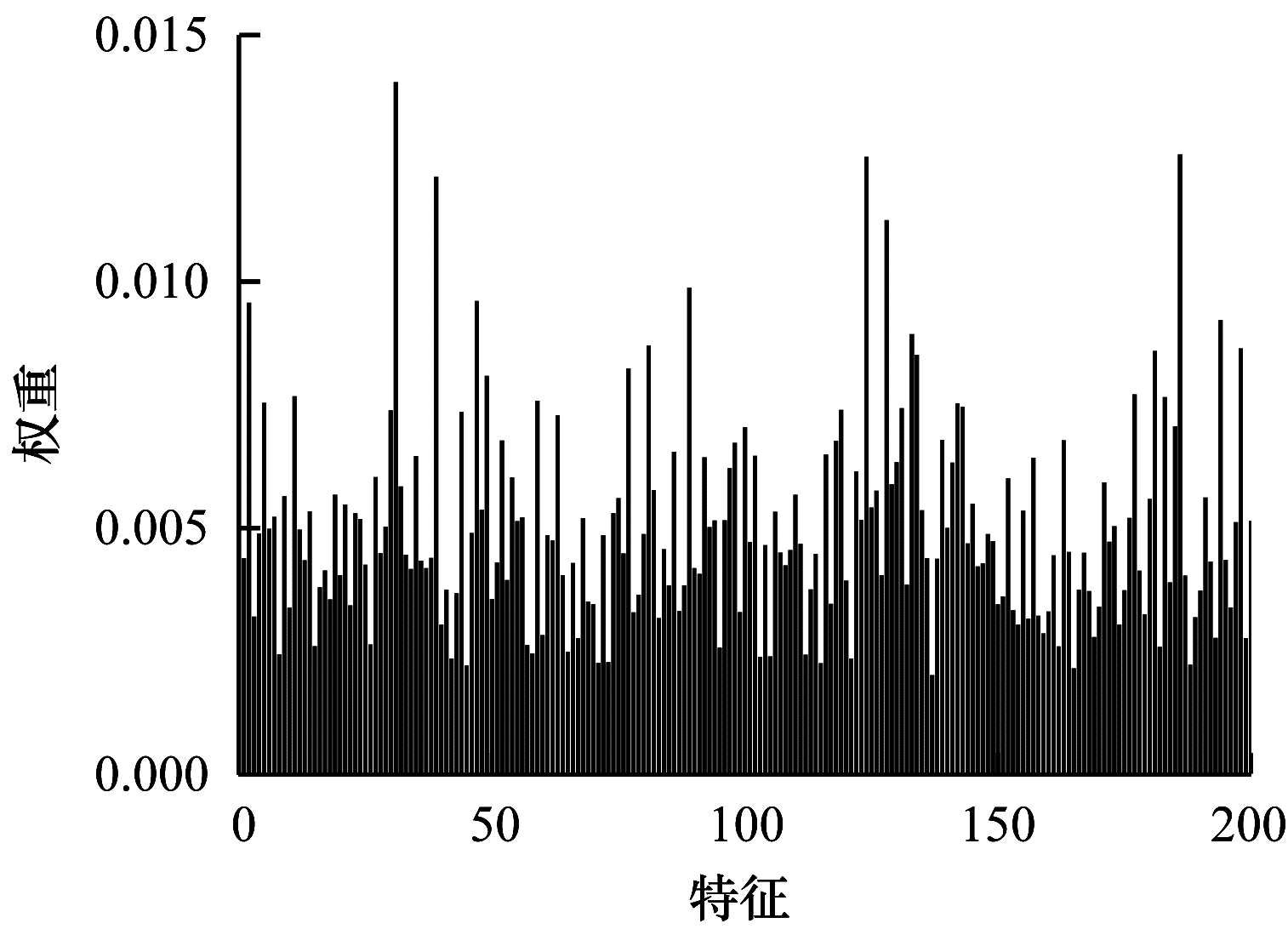
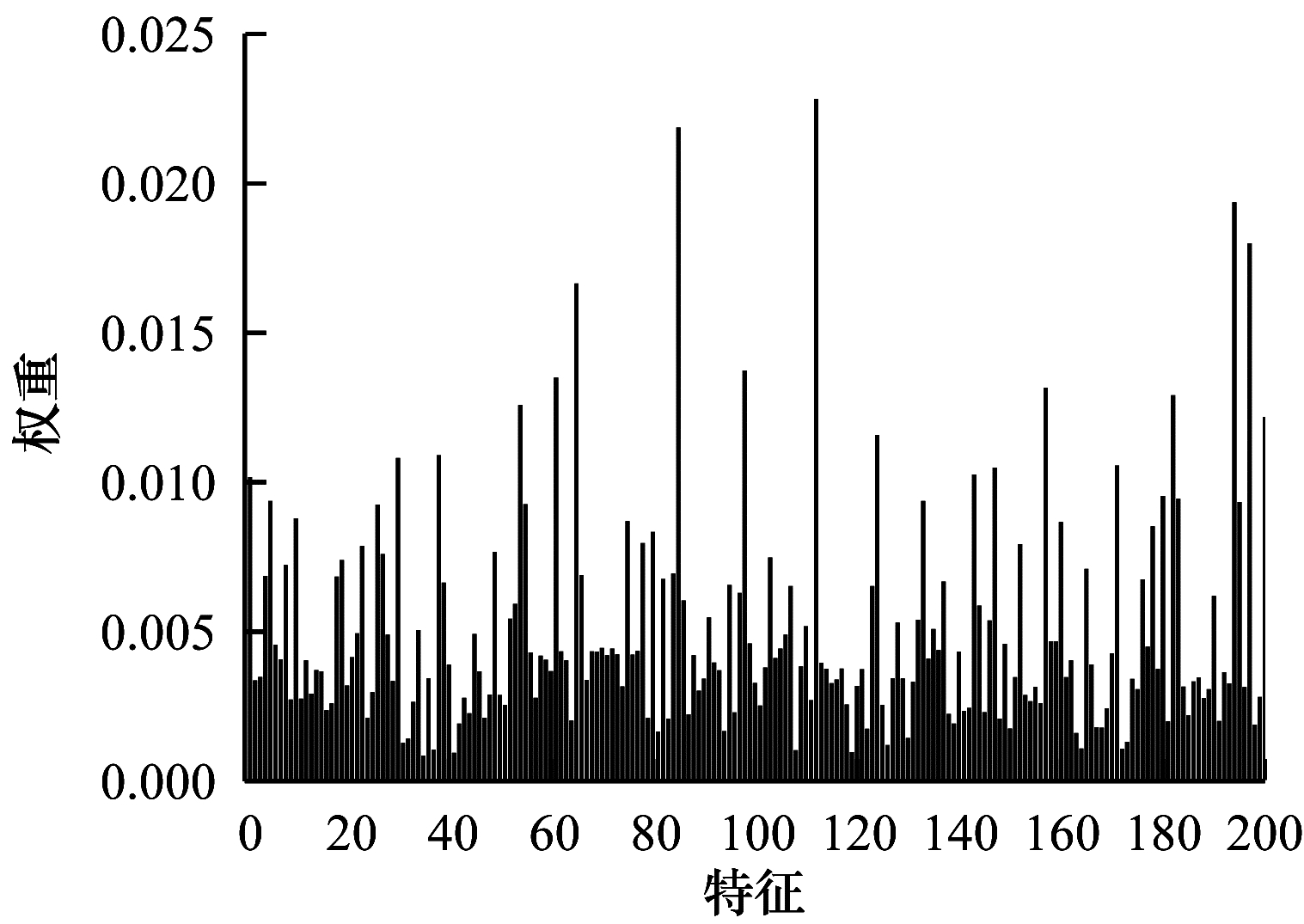
由于特征权值有部分是稀疏的，因此在某些维度上判别性较低。图 5~图 7给出不同数据集下学习到的各个特征的不同权重，图中横坐标为200维特征，纵坐标为权重。根据学习到的特征权重值可以区分有效特征、噪声特征、无用特征，因此，自动学习权重的方式可以学习判别性低的特征，从而有效指导后续的聚类工作。

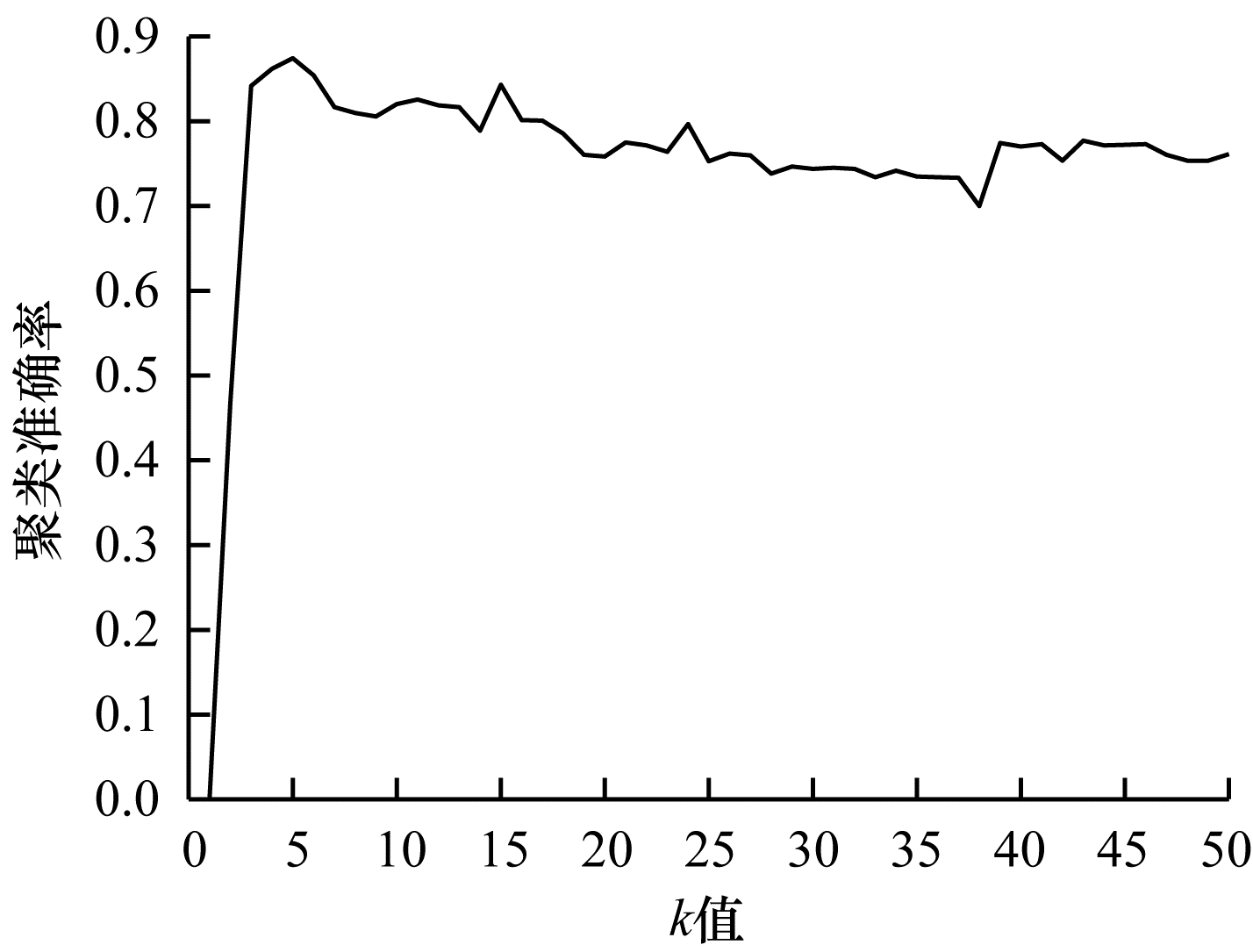
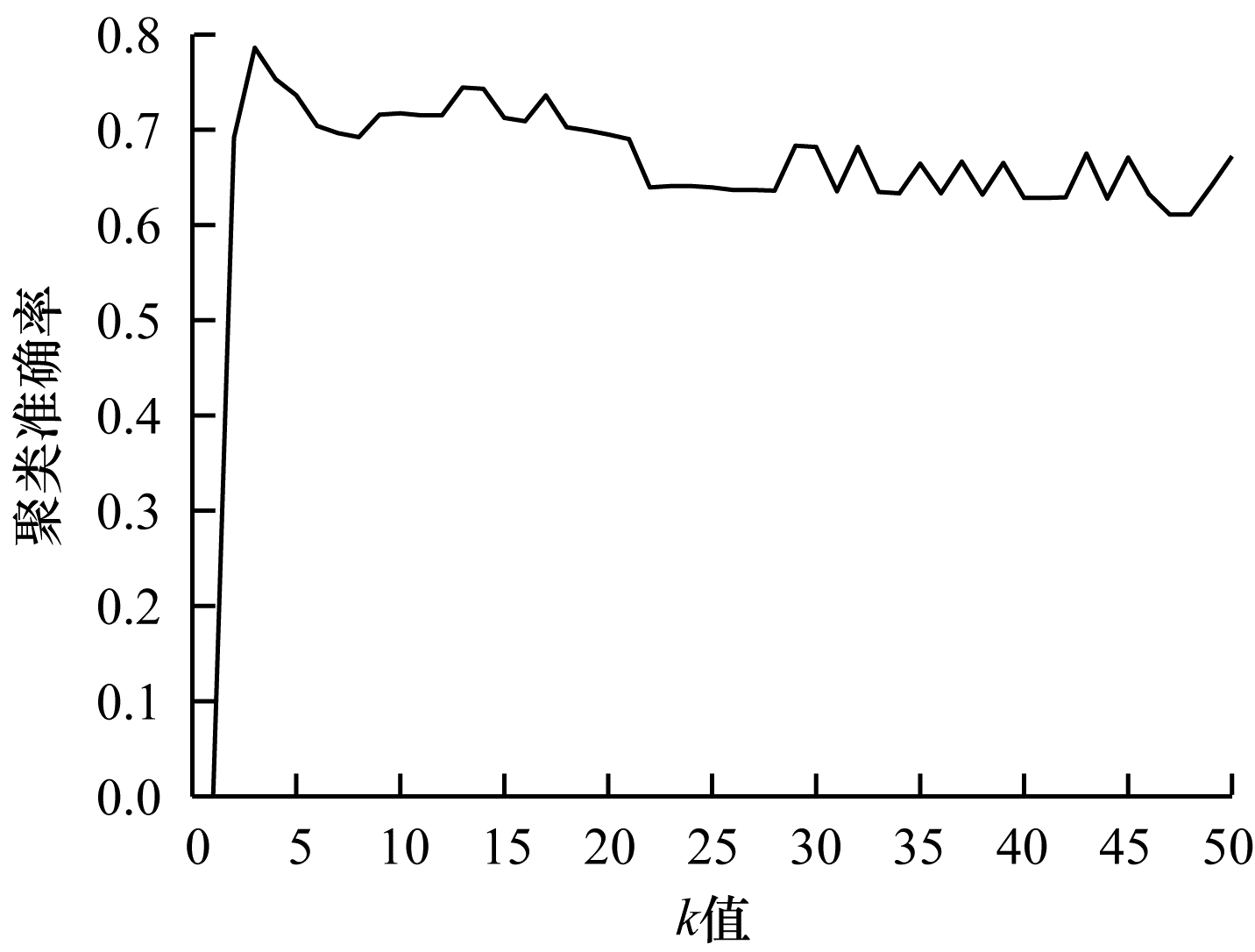
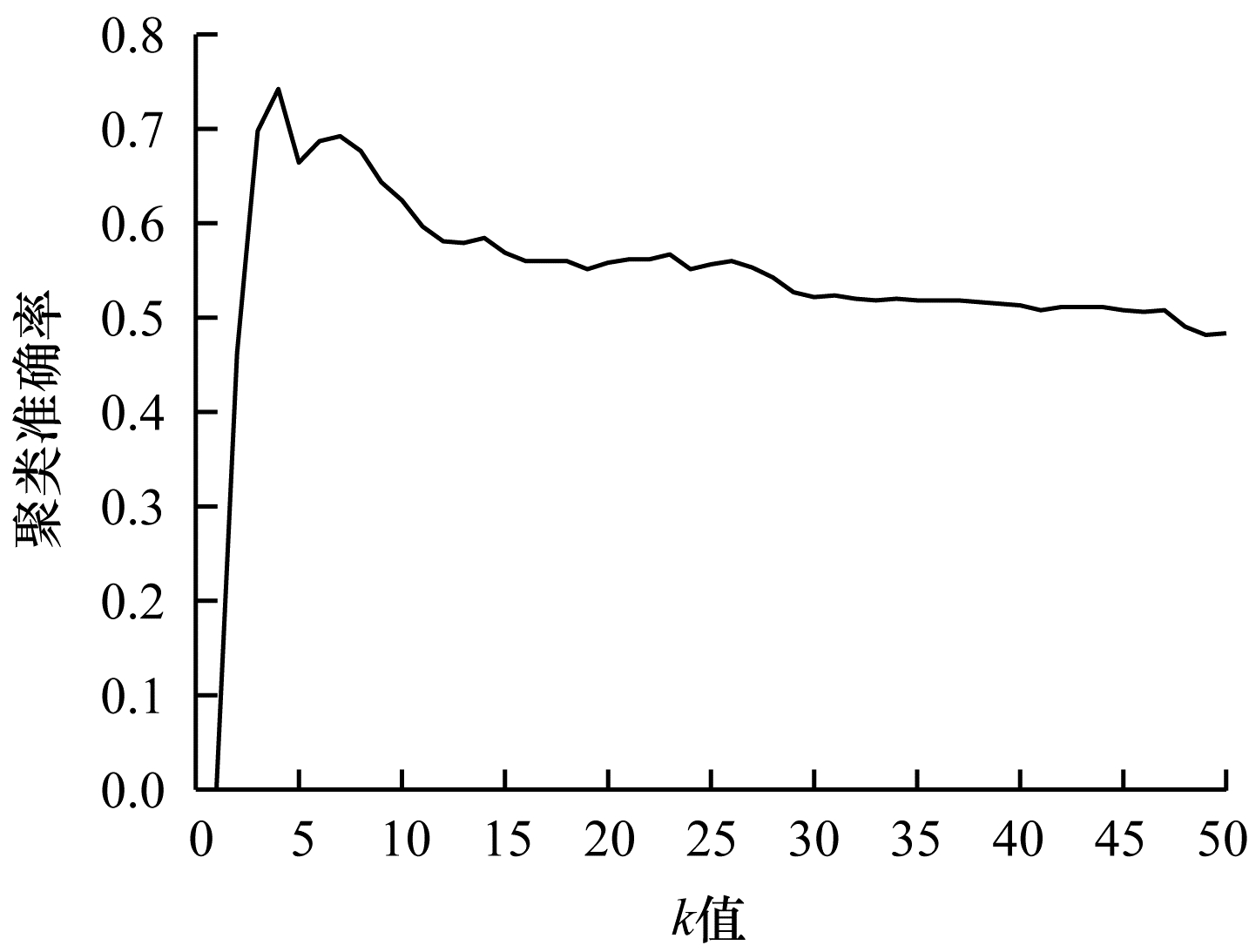
本文相似图学习方法与CAN、SWCAN算法相同，近邻数$ k $值在很大程度上影响了聚类准确率，为了测试$ k $值变化对算法性能的影响，将$ k $的取值区间设置为（2，50）以显示不同的聚类结果。通过图 8~图 10可以看出，在COIL-20数据集上，当$ k=5 $时聚类准确率达到最优，在ORL数据集上，当$ k=3 $时聚类准确率达到最优，在UMIST数据集上，当$ k=4 $时聚类准确率达到最优。从中可知，$ k $值对于聚类效果较为敏感，通过对$ k $值进行调整能够提升算法性能。

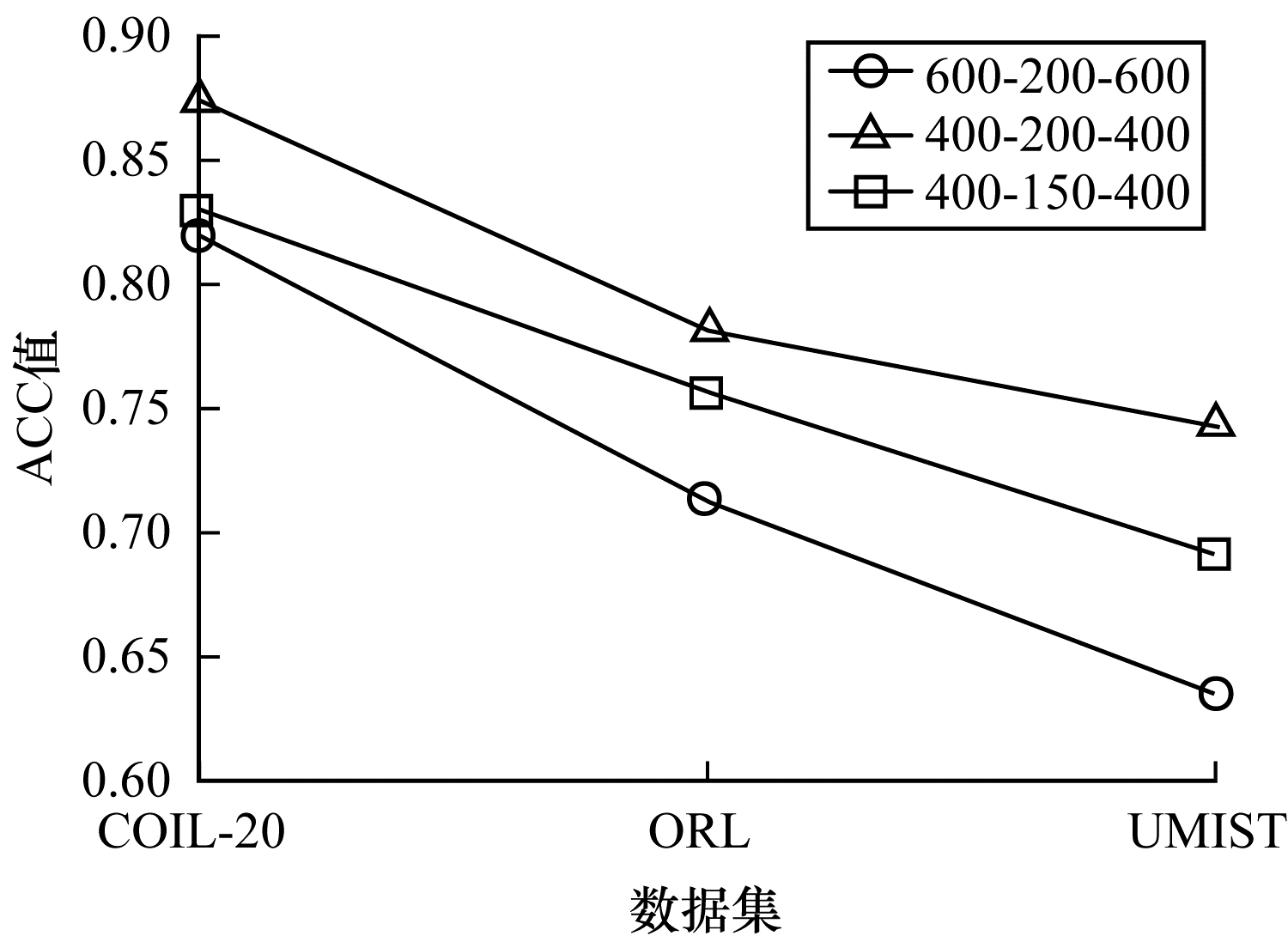
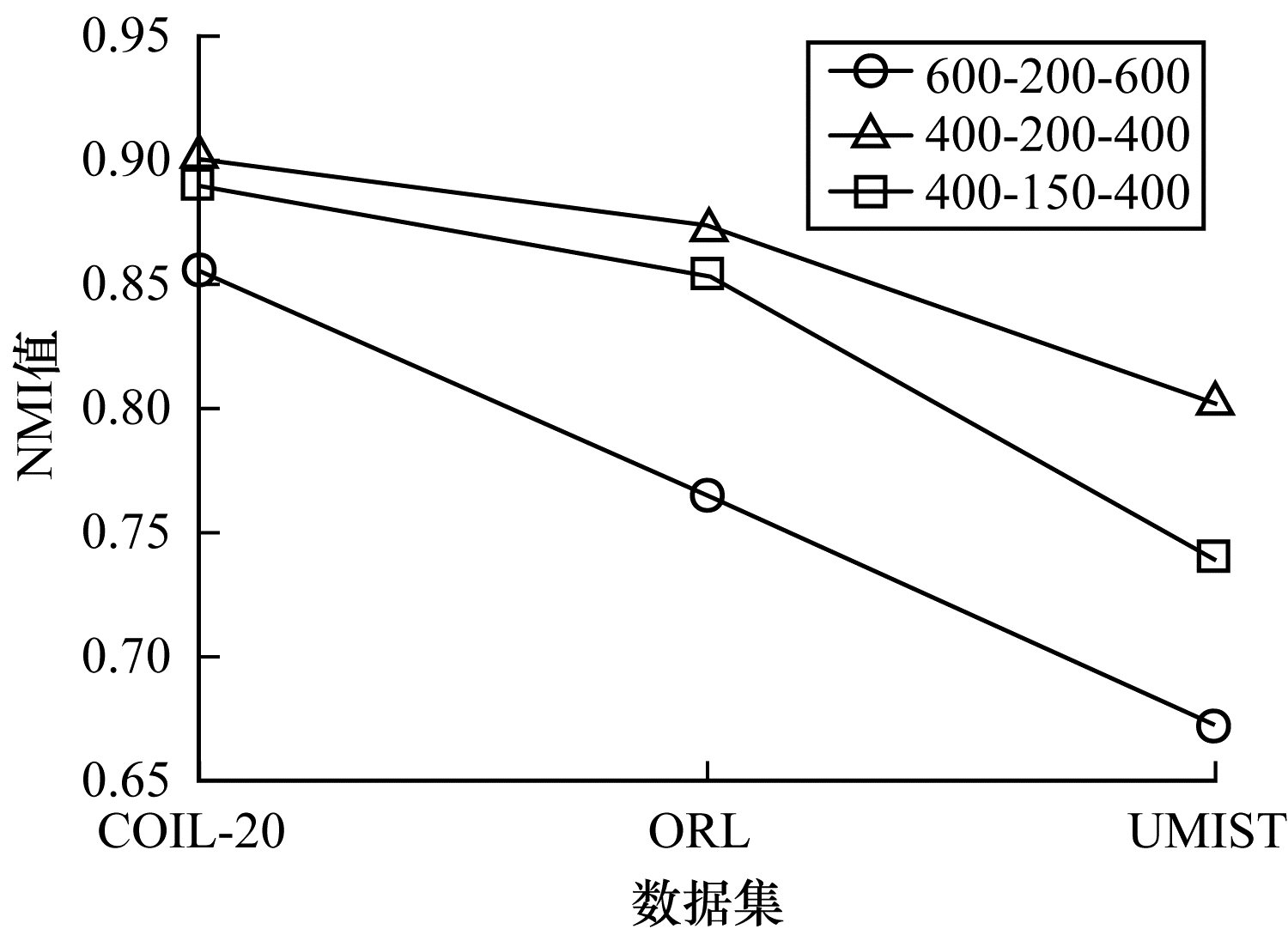
为了研究深度网络中隐藏层的大小对算法性能的影响，分别使用600-200-600、400-200-400、400-150-400这3种不同维度的隐藏层进行实验，结果如图 11、图 12所示。从中可以看出，当隐藏层的维度设置为400-150-400时，算法的ACC与NMI值均低于400-200-400，但均高于600-200-600；当隐藏层的维度设置为600-200-600时，3个数据集下算法的ACC与NMI值均低于其他2种情况。因此，深度网络的隐藏层维度设置为400-200-400时最优。

4 结束语

近年来，子空间聚类由于其计算效率高、易处理等特性而得到广泛研究与应用，然而，子空间学习方式在对高维非线性数据进行聚类时难以很好地捕获局部数据结构。因此，本文提出一种融合自动权重学习的深度聚类算法，通过端到端的学习方式，引入自编码器将特征投影到潜在空间并进行降维，从而实现子空间聚类。该算法能够兼顾全局数据结构与局部数据结构，并通过自适应学习特征权重的方式赋予潜在空间特征不同的权重，其中，赋予有效特征更高的权重，赋予噪声特征更低的权重，以此获得更好的聚类效果。在公开数据集上进行对比实验，结果表明，该算法的聚类效果优于LRR、LRSC、SSC等算法。下一步将在深度网络设计中加入生成对抗网络，以更精确地判别所学习到的特征，提升算法的聚类性能。