开放科学（资源服务）标志码（OSID）：

0 概述

深度神经网络的发展使图像分类、目标检测等计算机视觉任务得到了巨大的性能提升。随着计算机视觉处理任务日趋复杂，研究人员所设计的神经网络规模也逐步增大。神经网络的规模能够代表其学习能力，模型的参数量越多，模型容量越大，学习能力也越强。然而，针对不同的任务进行网络设计时很难确定神经网络的宽度和深度，通常研究者设计一个过参数化网络来保证学习能力，同时保证模型训练阶段能够收敛到一个比较好的局部最优点^[1-2]。但复杂的网络模型需要高额的存储空间和计算资源，在边缘设备的实际应用中，设备的计算性能和存储资源很难满足过参数化网络的性能需求。针对上述问题，可对模型进行压缩，以有效减少计算空间和时间消耗，提高模型的运行效率。神经网络的压缩方法主要有低秩分解、剪枝、量化、知识蒸馏、紧凑的网络设计等，其中剪枝方法简单有效，是目前的研究热点。

模型剪枝应设计可保证模型精度不损失的有效压缩模型，关键问题在于如何评价神经元的重要性和怎样移除神经元。剪枝算法可分为非结构化剪枝和结构化剪枝两种方式。非结构化剪枝是一种细粒度的剪枝方式，其直接针对模型中的参数进行剪枝，通常会根据权值、梯度等不同的方面衡量参数的重要性，不重要的参数会被剪除。非结构化剪枝能够有效地压缩模型，但是得到的稀疏权重矩阵需要特殊的硬件设备支持。结构化剪枝是对模型中的滤波器、通道等结构进行剪枝，通过在损失函数中加入卷积核中权值L1、L2正则项的方法评价卷积核的重要性^[3]。结构化剪枝方式对于网络每一层都需要设定超参数，并且在进行剪枝时网络需要迭代多次才能收敛。除了在损失函数中对卷积核权重加入正则化的方式评价卷积核的重要性之外，也有研究利用Batch Normalization中的γ参数来评价特征图的重要性^[4]，通过卷积核与上层特征图卷积得到本层特征图，通过γ参数评价特征图间接实现对卷积核的评价。结构化剪枝算法实现简单且不需要硬件设备支持，但是评价滤波器重要性时也同样从卷积核、通道等结构出发，无法对单个神经元的重要性进行评价。

模型的梯度信息与损失函数直接相关，利用梯度信息能够剔除影响模型收敛的冗余参数，在保证压缩参数量和计算量的同时提高模型性能。直接利用训练好的模型梯度信息相比加入惩罚因子、利用Batch Normalization中的γ参数等学习化的方法更简单有效。为了最大限度剔除神经网络中的冗余参数，本文采用权重梯度的绝对值对卷积核中的神经元进行量化，设置不同阈值，利用网格搜索的方式获取剪枝前后剩余参数量差值，通过计算参数量差值曲线的曲率最大值，确定参数量不发生明显变化时网络层的剪枝权重阈值。本文算法只需要对网络进行一次剪枝即能重新训练恢复模型精度，而无需经历多次剪枝-重训练的重复循环过程。

1 相关工作

利用模型参数的绝对值大小评估神经元重要性是模型剪枝操作中用来剔除不重要神经元最直接的评价方式。文献[5]提出以模型中权重的大小表征其重要程度，并将模型中权值低于某个阈值的权重参数置为0，然后通过重新训练的方式恢复模型精度。这种将某个权重直接归零的方式属于非结构化剪枝方法，此类方法能够有效地压缩模型，但是需要特殊的硬件设备支持。文献[3]计算一个卷积核内所有权值绝对值之和来表征每层中该卷积核的重要性，根据权重绝对值之和对卷积核进行排序，剔除权重绝对值之和最小的卷积核。在CIFAR10数据集上，该方法可使VGG-16的推理成本相比剪枝前降低34%，ResNet-110最高可降低38%，其通过在损失函数中加入L1、L2正则项的方法评价卷积核的重要程度，对于每一层都需要设定超参数，并且进行剪枝时网络需要迭代多次才能收敛。也有研究^[6]以group Lasso的方式获取稀疏化权重，将滤波器的权重分成多个组，通过对每个组的权重值进行L1正则化获取稀疏权重，实现对模型的压缩。

除了采用权值的方式之外，也有研究^[7-9]结合梯度值与模型权重进行剪枝。文献[7]将模型剪枝视作优化问题，通过泰勒展开式评价卷积核参数全部为0时对损失函数的影响，最终得到参数值与其梯度值的乘积来评价神经元的重要性。但该方法每完成一个卷积核的剪枝过程就需要重新训练一次网络恢复模型精度。文献[8]提出在深度模型训练之前多次采样部分训练数据，利用损失函数关于权重连接的梯度决定不同权重连接的重要性。该方法只需要一次剪枝操作即可实现权重重要性评价，避免了剪枝-微调的迭代过程。文献[9]通过计算数据的反向传播梯度得到损失变化的估计值，使用权重对应的梯度值量化所有权重元素的重要性，并将权重按梯度绝对值升序排序，去除不重要的权重。上述3种方法都属于结构化剪枝方式，通常会对滤波器、通道等结构进行重要性评估，然后去除不重要的滤波器和通道。

除了基于度量标准的方法判断神经元的重要性之外，还有采用参数的熵值^[10-11]、最小化特征输出重建误差^[12-13]等方法。这些方法以神经网络的卷积核或通道为最小单位进行量化，通过度量剪枝前后信息传递的完整性对模型进行剪枝，但都与结构化剪枝的方法类似，在剪枝过程中需要对网络进行多次训练，耗费了大量时间。非结构化剪枝方法虽然在剪枝过程中无需多次训练并且对神经网络的单个神经元进行了细粒度评价，能够取得很好的压缩效果，但是压缩后的模型需要专用硬件和算法库的支持，不具备通用性。

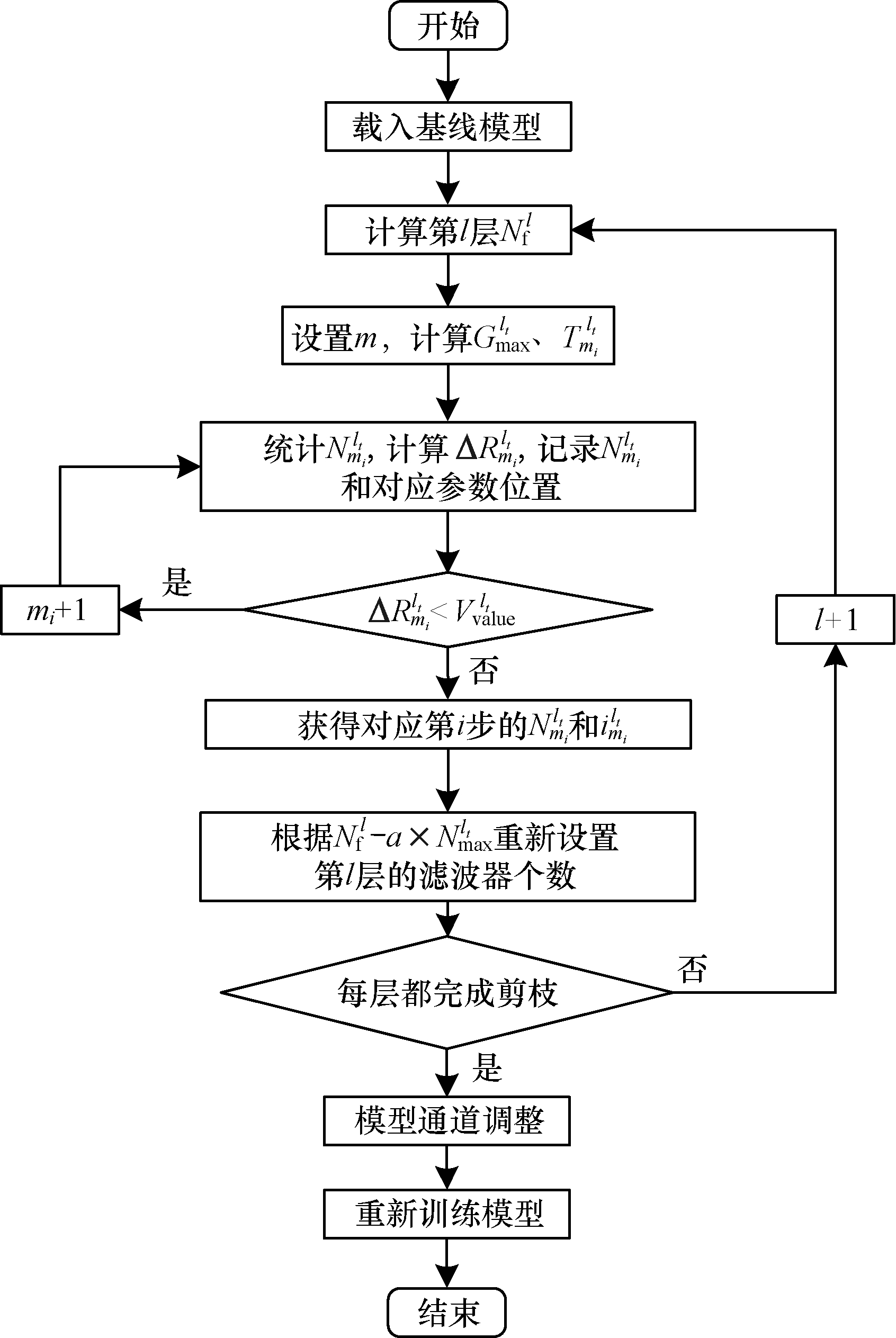
2 卷积核自适应阈值剪枝算法

本文算法根据反向传播的梯度绝对值来衡量神经元的重要性，利用多次搜索到的参数阈值自适应确定不同网络层的剪枝阈值，通过剪枝阈值调整卷积核个数，从而对模型进行压缩。在此过程中，网络执行一次数据迭代即可完成模型压缩，对压缩模型进行重新训练即可恢复模型精度。

2.1 基于梯度衡量准则的剪枝算法

本文算法采用梯度绝对值作为评判滤波器中权重重要性的依据，统计模型中梯度绝对值的最大值$ {G}_{{\mathrm{M}}_{\mathrm{l}}} $，在（0，$ {G}_{{\mathrm{M}}_{\mathrm{l}}} $）范围内设置间隔值，利用梯度间隔值以网格搜索的方式获取2次剪枝后剩余参数量的差值，根据剩余参数量的差值求取曲率，据此确定滤波器的剪枝阈值。在算法自适应获取到剪枝阈值后，将滤波器中小于梯度阈值的权重设置为0，统计每个滤波器中非零权重的数量，将小于$ a\times {N}_{\mathrm{m}\mathrm{a}\mathrm{x}} $的滤波器剪去（$ 0 < a < 1 $），保留剩下的滤波器个数，最后通过修改卷积核进而决定下一层产生的通道数。本文算法流程如图 1所示，具体步骤如下：

步骤1  载入利用图像和标注实例训练完成的基线模型，选择需要剪枝的网络层。

步骤2  统计基线模型第$ l $层滤波器中所有卷积核个数$ {N}_{\mathrm{f}}^{l} $，其中，$ l $表示当前网络层数，$ l=\mathrm{1, 2}, \cdots $。

步骤3  计算第$ l $层、第$ t $个卷积核中的参数$ {P}^{{l}_{t}} $、所有梯度值$ {G}^{{l}_{t}} $及所有参数量$ {N}_{\mathrm{p}}^{{l}_{t}} $。

步骤4  计算$ {G}^{{l}_{t}} $绝对值的最大值$ {G}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}} $，设置搜索步数m，计算每步搜索对应的阈值$ {T}_{{m}_{i}}^{{l}_{t}}={G}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}}\times \frac{{m}_{i}}{m} $，其中，$ {m}_{i}=\mathrm{1, 2}, \cdots , m $。

步骤5  根据阈值$ {T}_{{m}_{i}}^{{l}_{t}} $统计梯度矩阵中小于阈值$ {T}_{{m}_{i}}^{{l}_{t}} $的参数个数$ {N}_{{m}_{i}}^{{l}_{t}} $，计算第$ {m}_{i} $步的剩余参数量$ {R}_{{m}_{i}}^{{l}_{t}}={N}_{p}^{{l}_{t}}-{N}_{{m}_{i}}^{{l}_{t}} $，根据每步搜索剩余参数量计算两次搜索间隔的剩余参数差$ \mathrm{\Delta }{R}_{{m}_{i}}^{{l}_{t}} < {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $。

步骤6  重复步骤3~步骤5，得到不同阈值$ {T}_{{m}_{i}}^{{l}_{t}} $下第$ l $层、第$ t $个卷积核的所有$ \mathrm{\Delta }{R}_{{m}_{i}}^{{l}_{t}} $，当$ \mathrm{\Delta }{R}_{{m}_{i}}^{{l}_{t}} $小于设定的阈值$ {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $时停止搜索。通过阈值$ {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $确定停止搜索的步数$ {m}_{i} $，根据$ {T}_{{m}_{i}}^{{l}_{t}}={G}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}}\times \frac{{m}_{i}}{m} $计算$ {m}_{i} $下对应的梯度绝对值$ {T}_{{m}_{i}}^{{l}_{t}} $，记录梯度绝对值小于$ {T}_{{m}_{i}}^{{l}_{t}} $的参数位置$ {i}_{{m}_{i}}^{{l}_{t}} $。

步骤7  重复步骤2~步骤6，根据步骤6获得第$ l $层网络所有卷积核的$ {N}_{{m}_{i}}^{{l}_{t}} $值，将卷积核中梯度绝对值小于$ {T}_{{m}_{i}}^{{l}_{t}} $的$ {i}_{{m}_{i}}^{{l}_{t}} $的对应参数值置为0，统计滤波器中所有卷积核非0的参数数量$ {N}_{\mathrm{n}\mathrm{z}}^{{l}_{t}} $。

步骤8  计算第$ l $层所有卷积核$ {N}_{\mathrm{n}\mathrm{z}}^{{l}_{t}} $的最大值$ {N}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}} $，对滤波器中数量小于$ a\times {N}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}} $的卷积核进行裁剪，利用$ {N}_{\mathrm{f}}^{l}-a\times {N}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}} $得到的结果，重新设置第$ l $层卷积核的个数。

步骤9  重复步骤2~步骤8完成所有层的卷积核个数计算。

步骤10  获取待剪枝的所有层卷积核个数后，对网络模型进行卷积核个数调整。

步骤11  进行重新训练。

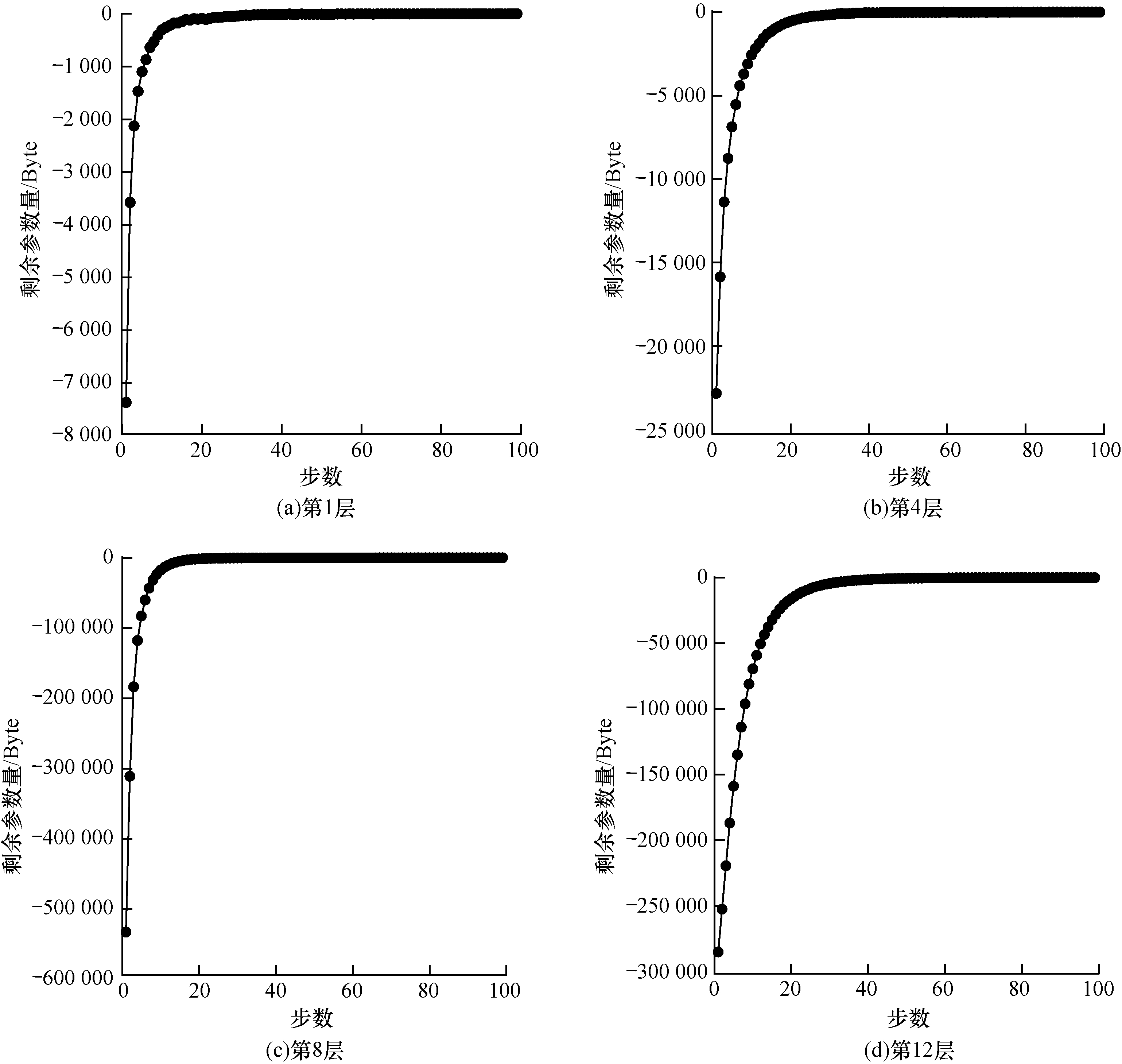
2.2 卷积层自适应剪枝阈值方法与通道调整

本文算法中的自适应阈值是在每层网络中设置不同的剪枝参数量，通过网格搜索的方式查找神经网络中不同网络层的卷积核所对应的剪枝阈值，根据每次搜索后的剩余参数量确定不同卷积层中卷积核内置零的冗余参数。对于剪枝算法流程中的阈值$ {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $，先通过求取剩余参数量的曲率半径，再根据最大曲率半径对应的剩余参数量得到不同卷积层对应的剪枝阈值。现有神经网络设计多呈金字塔型，网络层数越深，网络的卷积核个数越多，参数量越大。针对不同网络层的参数量，计算每个网络层中权重参数对应的梯度绝对值的最大值，根据设置的搜索步数上限和最大绝对值梯度确定该网络层的多个搜索阈值，通常搜索步数上限设置为100。利用梯度绝对值衡量权值重要性，在设置不同梯度阈值时，剩余参数量的变化如图 2所示。

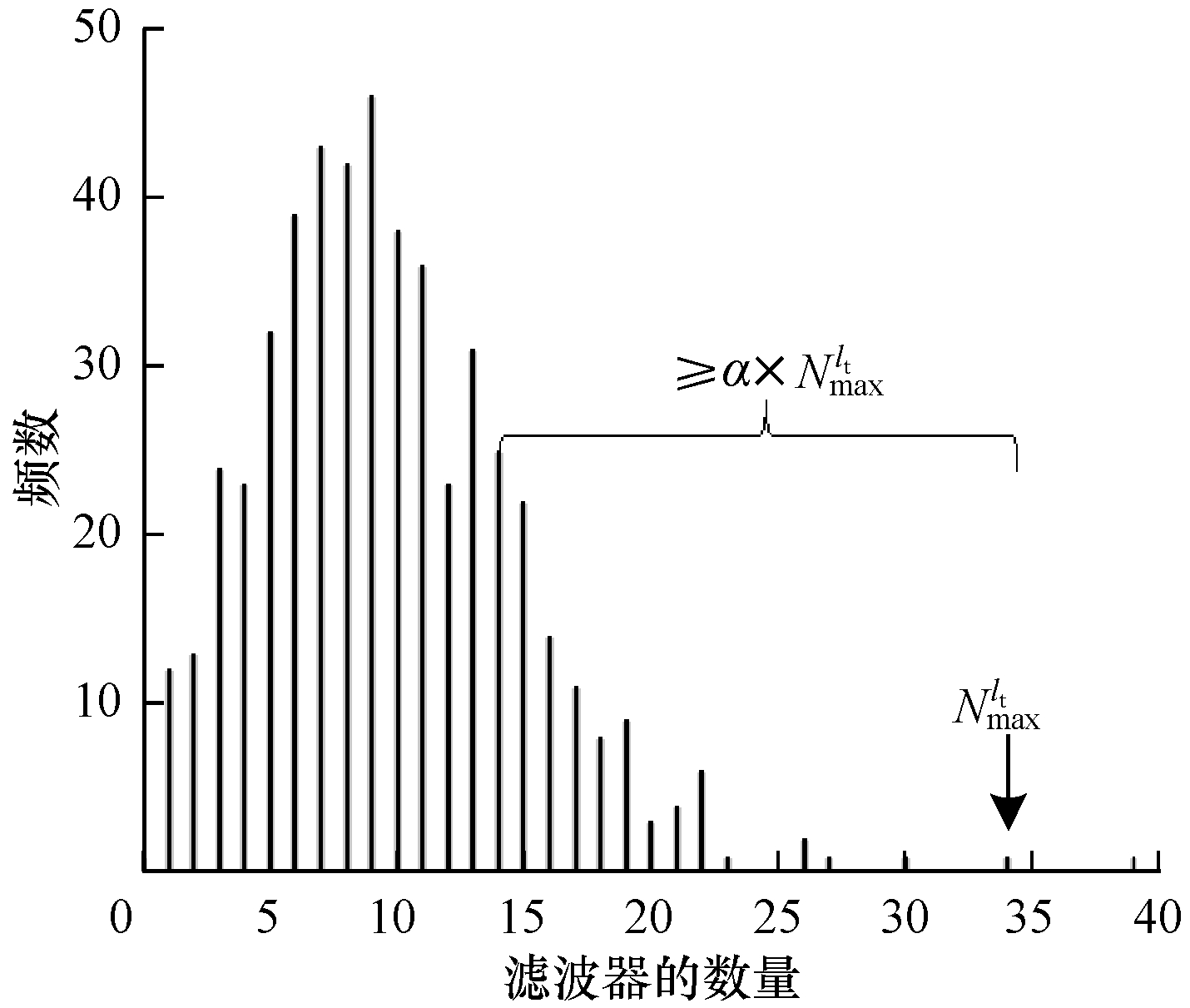
由图 2可以看出，当网格搜索达到20~50步时，剩余参数量会明显减少，表明大量不重要参数需要被减除，通常达到50步以后剩余参数量趋于稳定。根据不同的梯度阈值能够获取所有网格搜索阈值下的剩余参数量，对所有离散点进行数据平滑后，通过求取剩余参数量的最大曲率半径，对不同滤波器自适应地获取梯度阈值$ {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $。如图 2所示，不同网络层的阈值$ {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $基本上在两次间隔搜索的参数差值即将不发生变化之前确定。根据阈值$ {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $确定不同滤波器所用的剪枝步数$ {m}_{i} $，最终由$ {T}_{{m}_{i}}^{{l}_{t}}={G}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}}\times \frac{{m}_{i}}{m} $可得每个卷积核中剪枝的参数梯度阈值，将卷积核中梯度值小于$ {T}_{{m}_{i}}^{{l}_{t}} $的参数值置零，再统计所有滤波器中卷积核的非零个数，对数量小于$ a\times {N}_{\mathrm{m}\mathrm{a}\mathrm{x}}^{{l}_{t}} $的卷积核进行裁剪，具体如图 3所示。整个剪枝过程通过自适应搜索得到的梯度阈值$ {v}_{\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{u}\mathrm{e}}^{{l}_{t}} $确定置零的参数在每个卷积核中的占比，超参数$ a $控制每层的剪枝比例。根据不同剪枝比例，一般设置$ a $为0.1、0.2、0.3、0.4、0.5，$ a $的值越大，剪枝比例越大。

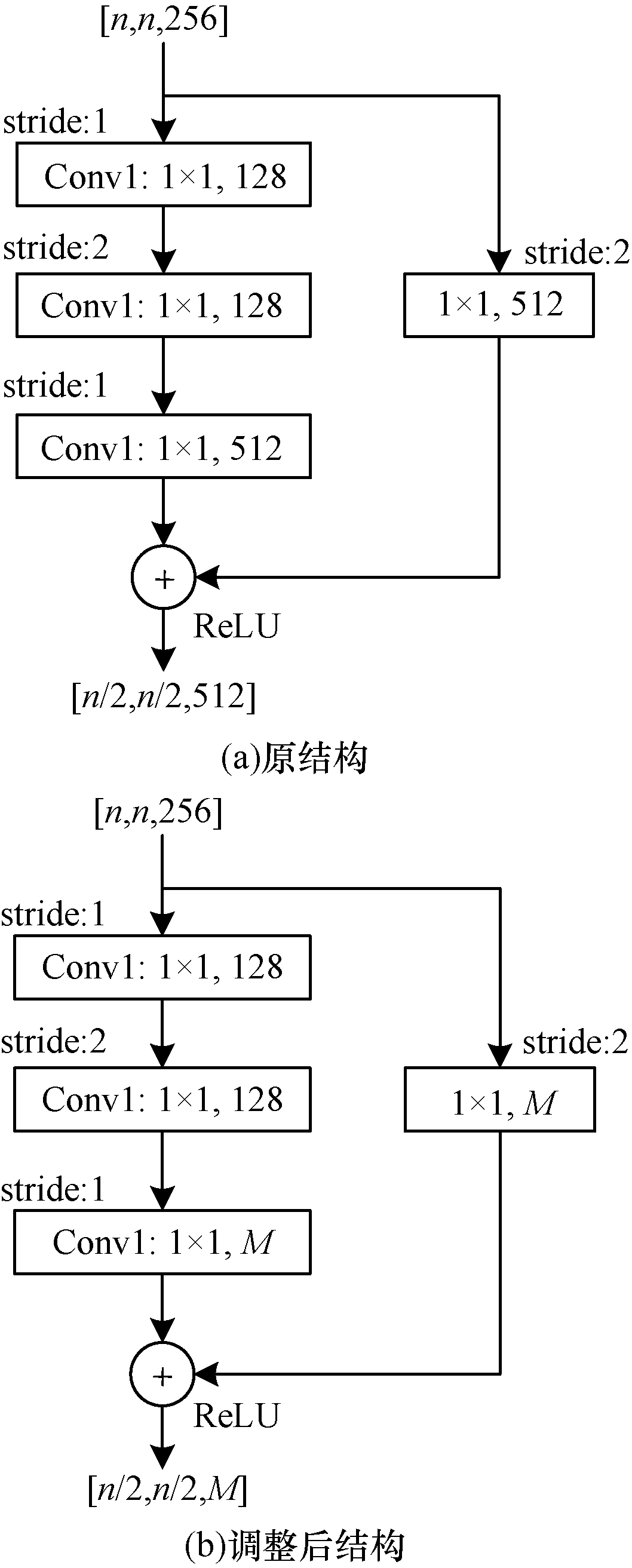
对残差网络完成剪枝后，会存在通道不匹配的问题。ResNet50的残差结构如图 4（a）所示，其中：残差分支包含3层卷积核用来改变滤波器核的尺寸和个数；捷径分支上有一个1×1的卷积层。如果对Conv1和Conv2进行剪枝只会影响到后一层的输入，如果对Conv3进行剪枝会影响主分支和捷径分支最后的相加操作。针对剪枝过程中残差结构内部残差分支和捷径分支通道变化的情况，采取改变捷径分支滤波器个数和残差分支最后一层滤波器个数的方式进行通道匹配，如图 4（b）所示。如果对Conv3进行剪枝，则要将残差分支最后一层滤波器的个数和捷径通道的滤波器个数设置为剪枝结果给出的M。

3 实验结果与分析

针对本文提出的结构化剪枝算法，分别在VGGNet^[14]、ResNet^[15]等分类模型和SSD^[16]、Yolov4^[17]、MaskRCNN^[18]等目标检测模型上进行模型压缩，所有的实验均基于PyTorch框架。

3.1 实验数据集

对于分类模型，在深度学习领域常用的图片数据集Cifar10上进行剪枝实验。Cifar10数据集包含10个不同类别，每个类别有6 000张彩色图片，每张图片大小为32×32像素。Cifar10的训练集有50 000张图片，测试集有10 000张图片。

对于目标检测模型，分别在公开的EgoHands数据集和安全头盔佩戴数据集SHWD上进行剪枝实验。EgoHands数据集有4 800张彩色图片，其中包含超过15 000多只手的图片，每张图片大小为720×1 280像素，3 874张图片用于训练，431张图片用于验证，479张图片用于测试。SHWD数据集有7 581张彩色图片，其中包含9 044个佩戴安全头盔对象和111 514个未佩戴安全帽对象，图像尺寸大小不一致，5 457张图片用于训练，607张图片用于验证，1 517张图片用于测试。

3.2 剪枝算法对比与性能评价指标

将本文提出的剪枝算法与PF^[3]、SFP^[19]、Rethinking^[20]等算法进行性能对比，评价指标为分类准确率（目标检测中用mAP衡量）、模型参数量和浮点运算数（Floating Point Operations，FLOPs）。其中：分类准确率表示分类模型的分类正确率；模型参数量表示神经网络模型在计算机中内存的占用量，决定模型文件的大小；FLOPs表示神经网络模型的计算量，用于衡量模型的复杂度。

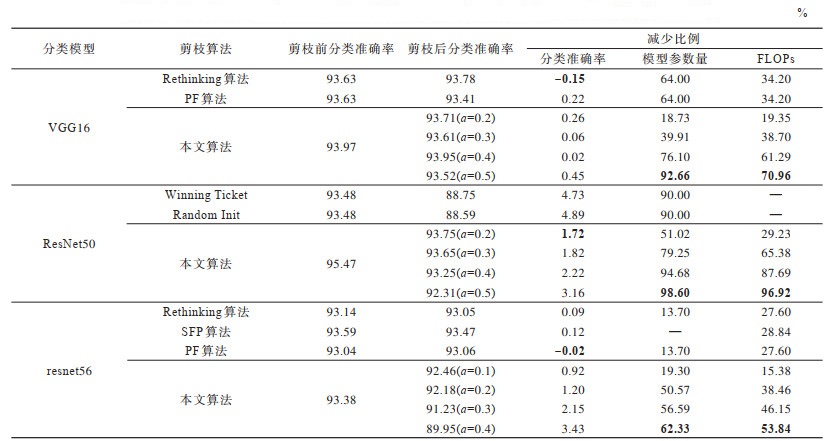
3.3 结果分析 3.3.1 分类模型剪枝实验

对分类模型VGG16、ResNet50和resnet56采用如下超参数设置训练：Epoch设置为200，初始学习率设置为0.1。优化方法采用随机梯度下降法，其中，momentum设置为0.9，weight_decay设置为0.000 5。学习率衰减策略采用余弦退火学习方法。表 1为利用不同算法对这两种分类模型剪枝后的实验结果对比，表中粗体表示最优结果，“—”表示文献中缺少对应数据，对比算法的实验结果直接使用文献[3, 19-21]中的数据。

由表 1可知，当设置不同超参数$ a $时，本文算法较其他算法使VGG16、ResNet50参数量减少了92%以上，计算量分别减少了70.96%和96.92%，网络参数量和计算量的压缩比例远高于其他算法。在VGG16的剪枝实验中，设置$ a $=0.5时剪枝效率最高，剪枝后模型精度相比原模型并没有明显下降，设置$ a $=0.4时精度损失最小。在ResNet50的剪枝实验中，网络的参数量和计算量最高分别压缩了98.60%和96.92%，压缩后的模型参数量仅为327.06 Kb，对比Winning Ticket和Random Init算法，本文算法在保证模型精度的同时能够大幅减少模型的参数量和计算量。在resnet56的剪枝实验中，原始模型参数量和计算量分别为853.02 Kb和0.13 GMac，远小于其他两种模型，对resnet56模型完成50%以上的参数量剪枝后模型更小，恢复精度训练更加困难。在权衡模型容量和精度损失后，resnet56设置超参数$ a $=0.2时达到最优剪枝效果，最终剪枝后模型分类准确率能达到92.18%。

3.3.2 目标检测模型剪枝实验

目前，目标检测模型剪枝实验相对较少，并且所用数据集和算法并不统一。本文使用EgoHands和SHWD这两个公开数据集对本文提出的剪枝算法进行测试，选择经典的目标检测模型进行剪枝实验，直接采用文献[22-26]中的数据进行对比，分别对比Faster RCNN^[22]、SSD^[23]、Yolo系列^[24-26]等目标检测模型采用不同剪枝算法的剪枝效果。训练模型的硬件设备设置为处理器Xeon Silver 4216、GPU显卡RTX 3070 8 GB；操作系统为Ubuntu18.0.4，python环境为3.6.10。在不同数据集上的训练超参数如表 2所示，其中，学习率衰减策略中的等间隔调整学习率gamma设置为0.91，剪枝前模型训练step_size设置为1，迭代次数设置为200，剪枝后的网络模型相对较小，恢复精度需要迭代更多的次数，通常将模型训练step_size设置为3，迭代次数设置为300。CSPdarknet53的网络设计相对轻量化，在达到同样参数压缩比例的情况下影响了模型的特征提取能力。CSPdarknet53模型压缩后恢复精度训练容易出现梯度爆炸的情况，损失函数会出现NaN的问题。为了防止CSPdarknet53出现梯度爆炸，加速网络收敛，先冻结全部的骨干网络迭代10次，再解冻训练全部参数恢复模型精度。

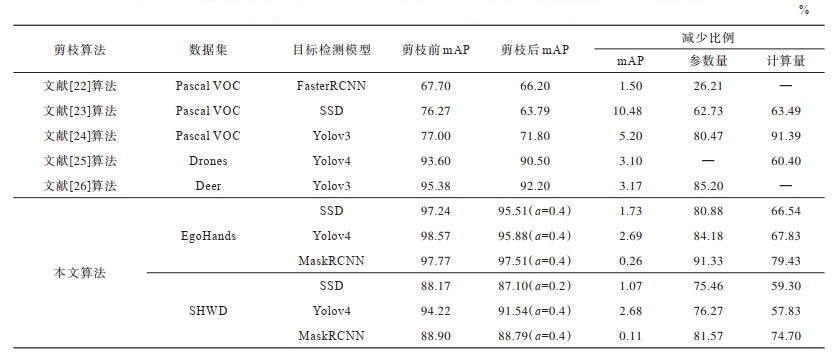
利用本文算法和文献[22-26]算法对3种模型剪枝前后的实验结果对比如表 3所示，其中，“—”表示文献中缺少对应数据。表中给出了不同剪枝算法实验所用数据集，在不同剪枝算法对比上主要分析模型压缩比率和精度损失情况。由表 3可以看出：利用文献[22]算法对骨干网络为ResNet50的FasterRCNN模型压缩后精度下降1.6%，但是模型参数量只压缩了26.21%；利用文献[23]算法对骨干网络为VGG16的SSD检测模型进行压缩，模型参数量压缩超过60%，但模型精度下降10.48%；文献[24]算法采用权值、激活值、梯度3种方式衡量神经元的重要性，最终Yolov3模型参数量压缩80.38%，精度下降5.2%。文献[22-24]实验数据都采用Pascal VOC数据集，该数据集中目标相对明显但是需要检测的物体种类较多，对模型过度压缩会影响模型精度。Drones和Deer数据集中目标种类相比Pascal VOC类别要少，但是目标像素占比相对较小，并且目标数量较多。利用文献[25-26]算法分别对Yolov4和Yolov3进行模型压缩，虽然能够达到较高的模型压缩比率，但是精度损失相对较大。

模型压缩多针对特定数据集进行压缩，以方便模型在边缘设备上部署。本实验采用EgoHands和SHWD两种数据集对3种算法进行测试。EgoHands数据集相对比较简单，3种原始检测模型精度相对比较高。实验结果表明，采用本文算法剪枝前后模型的参数量减少都超过80%，计算量减少都超过65%。SHWD数据集相比EgoHands较为复杂，相比EgoHands数据集上的实验，模型精度相对较低。为了保证剪枝以后模型精度不受太大影响，对模型压缩比例进行限制，在表 3中给出在两种数据集实验中权衡剪枝比率和模型精度最优的超参数$ a $。

3种模型的骨干网络不同，SSD采用VGG16作为骨干网络，VGG16整体结构比较简单，采用堆叠规整的卷积块结构进行特征提取，提取特征的能力有限。对SSD过度压缩容易影响模型精度，SSD在两个数据集上的压缩比率都超过了75%，在3种模型中SSD压缩比率最小。ResNet50采用残差模块解决训练退化问题，增强了深度网络的特征提取能力。从表 3的实验结果也可以发现，MaskRCNN的参数量压缩比例在SHWD数据集上达到81.57%，在EgoHands数据集上达到91.33%，而MaskRCNN的精度损失也最小，这充分证明了ResNet50相比其他两种骨干网络特征提取能力更强。CSPdarknet53同样采用了残差结构，但是相比其他两种骨干网络更轻量化，对应的模型容量也更小，在达到其他两种模型相当的压缩比例情况下会影响模型的精度。对比本文算法与其他算法的实验结果可以发现，在模型达到同样压缩比例的前提下，本文算法精度损失更小。

4 结束语

为了细粒度地评价卷积核中每个神经元的重要性，本文提出采用权重的梯度绝对值来衡量卷积核中每个权重的影响，采用网格搜索的方式获取剪枝前后剩余参数量差值，通过计算剩余参数量差值的曲率大小获取不同网络层的剪枝权重阈值，利用超参数$ a $控制最终的剪枝比例。在Cifar10数据集上对3种模型的超参数$ a $设置进行实验分析，在2种数据集上对常用的目标检测模型进行剪枝实验。实验结果表明，与Rethinking、PF等剪枝算法相比，本文算法能够在高压缩比例的情况下保证模型的精度，在常用目标检测模型上能够在保证模型精度的同时有效减少模型的参数量和计算量。后续将对知识蒸馏进行研究，通过多种网络压缩方法相融合的方式进一步提高压缩比例，同时使算法能够学习原网络的知识，保证压缩后的模型精度。