深度神经网络虽然已经在很多领域都取得了较好的效果, 但是其结构搜索仍然是一个具有挑战性的任务[1-2]。神经网络结构搜索通常是指在给定的一个数据集或问题情况下, 程序通过一定的算法自动探索出针对给定数据集或给定问题的最佳网络结构[3-4]。虽然目前有许多神经网络结构搜索算法被提出, 实现了卷积神经网络或循环神经网络结构的自动化设计过程, 但是搜索算法在探索过程中, 不可避免地需要对当前探索的网络结构性能进行评价, 而目前尚没有在不经过训练的前提下能够准确得到网络准确率的方法。因此, 搜索算法在搜索过程中需要不断地对待评估网络结构进行训练和评估, 这将非常耗时。一个网络的充分训练可能需要几小时、几天甚至更长的时间, 而网络结构搜索算法通常又需要探索成百上千甚至上万的结构, 如此庞大的计算量使得结构搜索的资源消耗和时间成本巨大。
为了降低网络结构搜索的时间成本, 很多自主式网络结构搜索算法都采取了一定的加速策略, 其中一种方法就是并行, 但是并行方式对设备资源要求较高, 并不适合多数应用场景, 原因是成百上千块的GPU资源基本只有大公司才能部署。另一个方法就是在搜索过程中只对网络训练有限的步数, 这也是多数搜索算法所使用的加速方式, 但是该方式存在一个问题, 例如, 有2个网络A和B, 当只训练少量步数(比如20步)时, A的验证集准确率比B高, 但是, 这不能说明充分训练(比如600步)后A的准确率也比B高, 因为少量步数的训练和充分训练2种情况下的网络结构和性能分布情况不一致, 即使在少量训练情况下网络结构取到了全局最优, 也不能保证该结构和充分训练后的全局最优结构相同或相似。
为了解决分布差异的问题, 一个可行的方法就是选取多个解。部分搜索算法在搜索结束后会选出一个或多个候选网络结构, 分别做一次完整的训练(比如600步), 再从中选出最佳网络结构, 也即选取当前最好的M个解(Top M-Best), 然后对最好的M个解充分训练后选取最优的解作为最后结果。但是, Top M-Best的方式存在一个问题, 在少量训练步数的分布(few-step distribution)上, Top M-Best集中于最优解附近, 然而这几个解在充分训练的分布(full-step distribution)上可能表现并不好; 相反, 当按照一定距离获取差异性更大的解时, 多样性解可能包含真正意义上的最优解。因此, 在少量训练步数分布上的最好的M个解, 可能会比较集中在最优解附近, 彼此非常相似, 以致在充分训练后可能并非都很好。Top M-Best解会分布在一个狭窄的空间范围内, 这不利于探索充分训练后的真正最优解。一个更好的方式就是选出的解不仅具有尽可能好的性能, 同时彼此的差异性应该更大, 这也即本文讨论的多样性解(Diverse M-Best)问题。
为了在少量训练步数的情况下提升搜索算法的性能, 本文提出一种多样性解的概念。和通常使用的最优性解(Top M-Best)相比, 多样性解一方面希望解具有高质量, 也即准确率或其他评价指标高, 另一方面希望选取的候选解彼此有一定的差异, 避免相似性解带来的局限性。为了寻找Diverse M-Best解, 需要解决2个问题, 一是如何来评价2个网络结构之间的距离, 二是如何来寻找多样性解。
目前, 针对网络结构之间的距离还没有较好的度量方式, 但是可以将网络结构和图(Graph)进行联系。在一个神经网络结构中, 可以将每一个操作看成图中的一个节点, 将不同层或不同操作之间的连接看成图中的边。由于网络结构可以看作一种图, 而网络对准能够寻找2个网络中的相似区域。因此, 可以通过网络对准技术来评估网络结构之间的距离。本文借鉴网络对准的方式, 从图的角度出发, 提出基于图的网络结构距离度量方法, 同时给出一种寻找多样性解的方式, 从而解决在网络搜索中由于训练步数不一致而引起的结果偏差问题。
1 相关工作 1.1 结构搜索目前, 网络结构搜索引起了研究人员的广泛关注, 尤其是自动化机器学习(Auto Machine Learning, AutoML)概念的产生, 使得网络结构搜索成为热点研究问题之一。在神经网络的结构搜索中, 主要有基于强化学习和基于进化学习的2个类方法。
基于强化学习的网络结构搜索主要利用RNN来序列化产生网络结构所需的参数。ZOPH[1]首次利用RNN网络作为一个控制器, 迭代式地产生一组结构编码, 从结构编码中解析对应的结构连接。RNN的训练是一种基于强化学习的方式, 其目标是最大化输出结构在验证集上的准确率。BAKER等人[5]提出基于强化学习中Q-Leammg的MetaQNN, 其将网络结构搜索模拟成马尔科夫决策过程, 基于已有结构探索下一阶段最优的组合情况。但是, 基于强化学习的方法的计算资源消耗巨大, 因此, 一些学者对其进行了适当的改进。文献[6]采用参数共享的方式减少计算量, 文献[7]利用网络参数转移和复用的方式, 加速一个新网络结构的训练过程。
基于进化学习的方法主要是将神经网络的结构进行编码, 转换成一个类似基因的序列, 然后通过随机的变异和重组操作不断产生新的网络结构编码。针对新产生的网络结构编码所对应的结构进行训练评估, 选取当前最好的若干个网络编码, 并以这批网络为基础, 重复上述步骤以产生一批新的网络, 如此不断迭代直至探索终止。文献[8]利用许多简单的构建模块以及常用的初始条件设定一个进化过程, 从简单的网络结构开始不断尝试更新和迭代, 最后找出和手动设计性能相当的网络结构。
近年来, 研究人员提出一些基于梯度的网络结构搜索方法。基于强化学习和基于进化学习的方法通常将结构的优化当作离散优化问题进行解决[9], 而基于梯度的方法则是将结构优化问题当作连续优化问题, 该类方法中具有代表性的就是DARTS[10]。DARTS搜索的空间是若干有序节点组合而成的结构单元, 其最核心的步骤是利用Softmax函数来选择连接, 优化后再选取Softmax输出概率最大的连接方式。文献[11]将网络结构嵌入到一个连续隐空间中, 使得空间中每一个点都对应一个网络结构, 而在连续空间中通过准确率预测函数的优化寻找准确率最高的点, 进而反向寻找出对应的网络结构。
1.2 网络对准网络对准主要是对于2个图网络中相似区域的匹配或校对。考虑2个图A=(VA, EA), B=(VB, EB), 其中, VA、VB分别是2个图的点集, EA、EB分别是2个图的边集, 即所有匹配的连接情况, 2个图的匹配就是寻找EL的一个子集M, 使得子集中每个边都不共享节点, 也即任一边(i, i′)∈M与任一边(j, j′)∈M包含的点可以形成一个四边形。网络对准在很多计算机问题中都得到广泛应用, 比如最大公共子图问题或二次匹配问题。网络对准通常就是如下的优化问题[12]:
| $ \mathop {\min }\limits_\mathit{\boldsymbol{P}} {\left\| {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{P}}^{\rm{T}}}} \right\|_{\rm{F}}} $ |
其中, A和B分别是2个待匹配网络的邻接矩阵, P是一个变换矩阵。网络对准也即寻找一个变换, 使得变换后2个矩阵尽可能一样, 通过这样的方式去寻找网络中的匹配区域。
一种典型的网络对准方法是IsoRank[13], 该方法充分利用所有点对的Kronecker积, 其目的是最大化输入网络结构的最大结构交叉匹配, 同时, IsoRank充分考虑了全局关系。IsoRank方法的主要思想来自蛋白质结构网络, 如果某一网络中某一个结构单元的邻域和另一个网络结构中某一结构单元的邻域非常匹配, 则这2个蛋白质结构就应该非常匹配。后续一些网络对IsoRank进行了拓展和补充。文献[14]将IsoRank拓展为多网络结构形式, 文献[15]利用解耦和分解方法, 将IsoRank拓展成适合更大规模数据的形式, 文献[16]则利用序列相似和矩阵迹分解来合并和寻找网络结构的对齐情况, 文献[17]针对稀疏网络结构对IsoRank进行了改进, 其将网络对准转换成一个整数二次型优化问题, 通过最大后验分配寻找次优解。文献[18]利用迭代投影梯度下降法来解决网络对准问题。文献[19]利用权重矩阵的最大化解决网络对准问题。文献[20]利用先验的可能连接情况, 对局部进行校准。文献[21]研究属性网络的对准问题, 并给出一种优化方式解决该问题, 此外, 其提出了一系列有效的对准方案, 同时考虑时间复杂度, 对对准方案做出了近似使得其可以在线性复杂度的情况下解决对准问题。文献[22]引进xNetMF方法来获取网络的节点相似情况, 并采取矩阵分解和slap-gram的方式优化网络, 从低秩矩阵的角度对相似矩阵进行分解, 使得其在大规模数据上也保持较高的速度。
2 网络结构距离度量多样性解不但具有较高的质量, 同时避免了相似性解带来的局限性。要解决多样性结构问题, 首先需要度量网络结构之间的距离。具体的度量方法不仅需要考虑网络结构中数据的流动情况, 也要注意节点操作特征以准确描述节点的相似性。用图G1(ν1, ε1)和G2(ν2, ε2)分别表示结构φ1和φ2, 其中, 节点集合ν1和ν2分别代表 2个网络结构中的操作集合, 边集合ε1和ε2分别代表 2个网络结构各个操作之间的连接情况, 也即数据在网络结构中的流动情况。本文同时考虑网络的数据流情况和操作情况, 提出一种度量网络结构之间距离的方法。
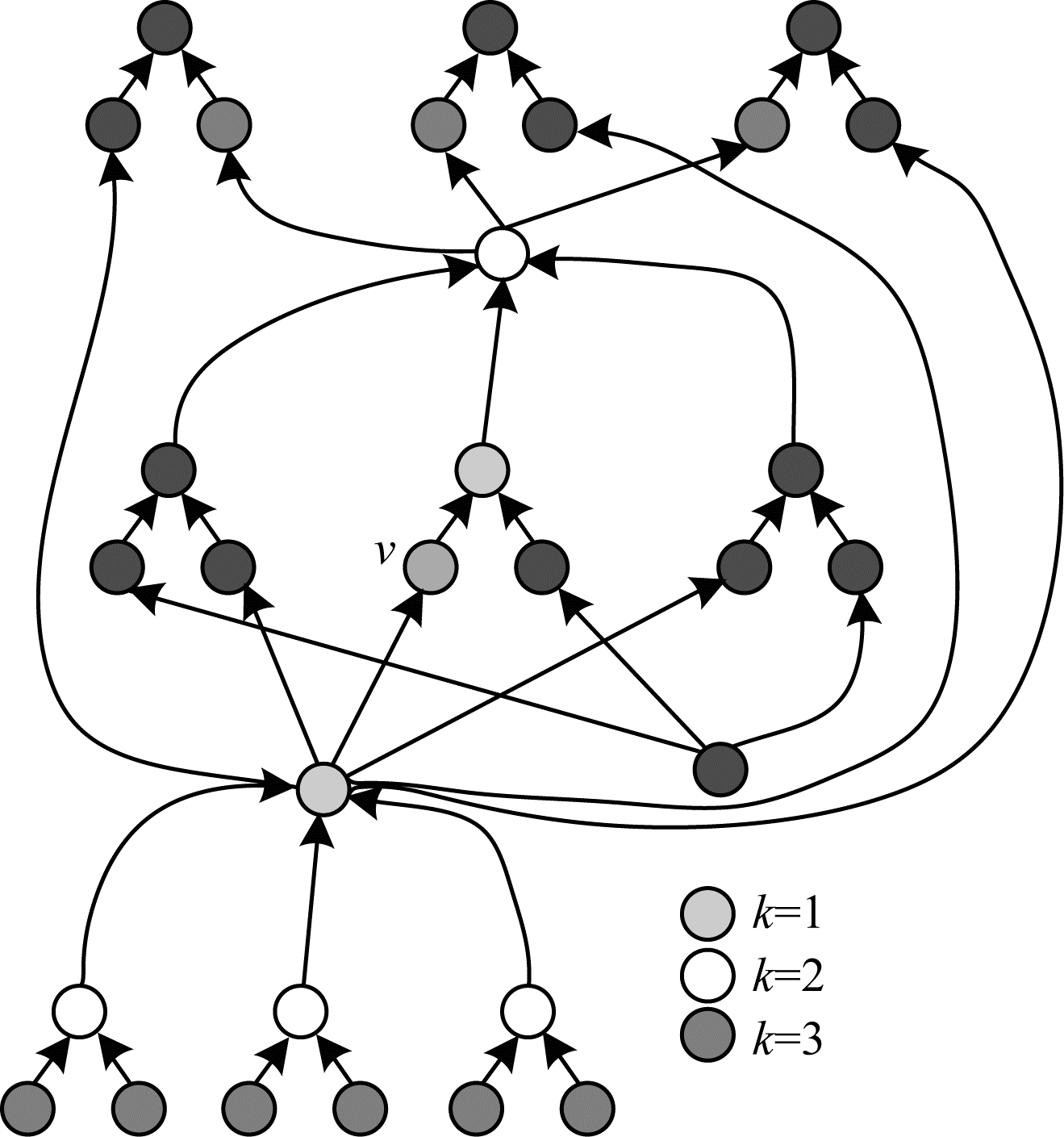
2.1 数据流特征数据流特征是对网络连接方式的概括和总结。在网络对准中, 有一个基本的假设就是相似的节点具有相似的度。由于网络中数据的流动是有向的, 因此在网络结构所对应的图中, 本文同时考虑出度和入度, 度的特征在一定程度上反映了网络的连接方式。将图中任意2个节点之间最短路径所包含的边的条数记为2个节点之间的距离。对于集合V中的一个节点ν, 记Nvk-表示图G中位于节点ν上游且距离ν为k的节点集合, 同理, Nvk+表示图G中位于节点ν下游且距离ν为k的节点集合。为了提取节点的数据流特征, 本文考虑距离该节点为k的邻域Nvk, 其中, Nvk=Nvk-∪Nvk+。
本文将入度信息和出度信息分别存储在向量dvk-和dvk+中, 其中, dvk-的第i个元素表示距离节点ν为k步的节点中入度为i的节点个数, 同理, dvk+的第i个元素表示距离节点ν为k步的节点中出度为i的节点个数。考虑区域性特征, 本文提取步数为K以内的不同等级的特征, 定义每个节点的特征如下:
| $ \begin{array}{l} \mathit{\boldsymbol{d}}_v^ - = \sum\limits_{k = 1}^K {{\gamma ^{k - 1}}} \mathit{\boldsymbol{d}}_v^{k - }\\ \mathit{\boldsymbol{d}}_v^ + = \sum\limits_{k = 1}^K {{\gamma ^{k - 1}}} \mathit{\boldsymbol{d}}_v^{k + } \end{array} $ |
其中, γ∈(0, 1)是一个衰减因子, 其控制不同邻域的影响程度。γ取值的影响因素包括其他节点与节点ν的距离、邻域内不同出入度的节点与节点ν的相似程度等。衰减因子的取值应根据节点的出入度信息、节点间距以及整体网络结构进行综合设置[20, 22]。
2.2 操作特征提取如图 1所示, 在一个网络结构图中, 不同节点通常进行不同的操作, 包括卷积操作、池化操作或拼接操作等。即使2个节点代表同样的操作类型, 其具体的操作也可能不一样。例如, 节点A和节点B都表示卷积操作, 但是节点A使用3×3大小的卷积核, 而节点B使用5×5大小的卷积核, 即节点A和节点B具体操作不同。操作的类型、通道数、尺寸、步长以及补齐等参数对相似性度量及距离度量都会造成影响。因此, 充分考虑操作本身的特征并提取上述参数能够提高距离度量的准确性。对于节点集合V中的某个节点ν, fν表示该节点的属性特征, fν的第i个元素表示第i个属性情况。需要注意的是, 每一个节点的属性特征向量维度是一致的, 如果某个节点不具有某一属性, 则对其设置一个默认的值, 比如0。
|
Download:
|
| 图 1 数据流特征邻域示意图 Fig. 1 Schematic diagram of data stream feature neighborhood | |
前文分别从网络的连接情况和节点本身的操作情况对网络结构进行了特征提取, 本节将进一步阐述节点之间的相似性度量, 为后续结构距离度量做准备。给定2个节点ν1和ν2, 综合考虑网络的连接情况和操作特征, 本文定义如下的节点相似性表达式:
| $ \begin{array}{*{20}{l}} {s\left( {{\nu _1},{\nu _2}} \right) = \exp \left( { - {\gamma _{{\rm{in }}}} \cdot {d_{{\rm{in }}}} - {\gamma _{{\rm{out }}}} \cdot {d_{{\rm{out }}}} - {\gamma _f} \cdot {d_f}} \right)}\\ {{d_{{\rm{in }}}} = \left\| {\mathit{\boldsymbol{d}}_{{v_1}}^ - - \mathit{\boldsymbol{d}}_{{v_2}}^ - } \right\|_2^2}\\ {{d_{{\rm{out }}}} = \left\| {\mathit{\boldsymbol{d}}_{{v_1}}^ + - \mathit{\boldsymbol{d}}_{{v_2}}^ + } \right\|_2^2}\\ {{d_f} = \frac{1}{{\left| {{\mathit{\boldsymbol{A}}_0}} \right|}}\sum\limits_{i \in {A_0}} 1 \left( {\mathit{\boldsymbol{f}}_{{\nu _1}}^i \ne \mathit{\boldsymbol{f}}_{{\nu _2}}^i} \right) + \frac{{\mathit{\boldsymbol{f}}_{{v_1}}^{\overline {{A_0}} } \cdot \mathit{\boldsymbol{f}}_{{v_2}}^{\overline {{A_0}} }}}{{\left\| {\mathit{\boldsymbol{f}}_{{v_1}}^{\overline {{A_0}} }} \right\| \cdot \left\| {\mathit{\boldsymbol{f}}_{{v_2}}^{\overline {{A_0}} }} \right\|}}} \end{array} $ |
其中, γin、γout和γf是常数因子, 控制数据流特征和操作特征在距离度量中的重要程度, A0是属性特征中非数值类型特征的索引集合,

|
Download:
|
| 图 2 df度量示意图 Fig. 2 Measurement diagram of df | |
为了获取2个网络结构如G1(ν1, ε1)和G2(ν2, ε2)之间的距离, 可以利用节点之间的相似性矩阵S。利用矩阵分解的方式, 将隐层节点投影到一个隐空间中再匹配和寻找相似节点, 优化问题如下:
| $ \mathop {\min }\limits_{F,Z} \left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{Z}}^ \bot }} \right\|_{\rm{F}}^2 $ |
其中, F是隐空间特征, Z是一组编码权重。
考虑到每个网络结构中可能有很多节点, 同时在搜索中可能需要计算成百上千个网络之间的距离, 如果每次的距离计算都进行一次矩阵分解优化, 算法的复杂度将很高, 在实验室条件下其时间成本也无法接受。文献[23]使用SVD分解的方式来近似对相似矩阵进行分解, 时间成本可以缩短一个数量级, 近似方法的准确度超过98%。因此, 本文采用SVD分解的方法, 对于一个非负对称的矩阵, 利用随机选取若干列的方式来对其进行近似。比如, 从矩阵M中按均匀分布的方式随机选取c列, 同时选取对应的c行, 彼此相交处得到一个方阵W, 对方阵W求伪逆得到逆矩阵W+, 则有M=CW+CT, CW+CT可以被认为是原矩阵M的一个近似。
参考文献[23]的方法, 本文也对相似矩阵进行近似。与随机选取不同, 本文在每一个结构中固定选取有限的p个节点作为该结构的代表性节点, 依据SVD分解的经典理论, 参考文献[23]并结合实验探索过程, 此处p取经验值p=lb|V|。本文认为关键性节点是节点度较大的节点, 即通过出入度信息来判断关键性节点, 类似交通系统中的枢纽, 其是一个网络结构中的关键性节点。本文按网络结构中节点度的排序情况对每个网络结构选取p个关键性节点。记Γ1和Γ2分别为结构图G1(ν1, ε1)和G2(ν2, ε2)的关键性节点集合, Γ=Γ1∪Γ2为待计算距离的2个网络结构的关键性节点总和, SΓ表示节点集合Γ中所有节点之间的相似性矩阵, 其中:
| $ {\mathit{\boldsymbol{S}}_\Gamma }(i,j) = s\left( {{v_i},{v_j}} \right),\forall i,j \in [0,|\Gamma |],{v_i} \in \Gamma ,{v_j} \in \Gamma $ |
相似性矩阵S∈Rn×n(n=|V1+V2|)可以被近似为:
| $ \mathit{\boldsymbol{S}} \approx \mathit{\boldsymbol{CS}}_\Gamma ^† {\mathit{\boldsymbol{C}}^ \bot } $ |
其中, SΓ$† $是SΓ的逆矩阵, C∈Rn×p表示网络结构和关键性节点之间的相似性矩阵。对SΓ$† $做SVD分解, 则有:
| $ \mathit{\boldsymbol{S}} \approx \mathit{\boldsymbol{CS}}_\Gamma ^† {\mathit{\boldsymbol{C}}^ \bot } = \left( {\mathit{\boldsymbol{CU}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{\frac{1}{2}}}} \right) \cdot {\left( {\mathit{\boldsymbol{CV}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{\frac{1}{2}}}} \right)^ \bot } $ |
令$F = \mathit{\boldsymbol{CU}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{\frac{1}{2}}}$, 其可以简单地看做是最小化‖S-FZ⊥‖F2的一组解。因此, 对于网络结构图G1和G2中的节点, 分别提取隐空间特征, 如下:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{F}}_1} = {\mathit{\boldsymbol{S}}_1}\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{\frac{1}{2}}},{\mathit{\boldsymbol{S}}_1} \in {\mathit{\boldsymbol{R}}^{{{\left| {{V_1}} \right|}^{ \times p}}}}}\\ {{\mathit{\boldsymbol{F}}_2} = {\mathit{\boldsymbol{S}}_2}\mathit{\boldsymbol{U}}{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{\frac{1}{2}}},{\mathit{\boldsymbol{S}}_2} \in {\mathit{\boldsymbol{R}}^{{{\left| {{V_2}} \right|}^{ \times p}}}}} \end{array} $ |
其中, S1表示G1中节点和关键性节点集合Γ中节点的相似性矩阵, S2表示G2中节点和关键性节点集合Γ中节点的相似性矩阵。在隐层空间中, 本文定义2个结构G1和G2之间的距离如下:
| $ \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}\left( {{G_1},{G_2}} \right) = \frac{1}{{\left| {{V_1}} \right|}}\sum\limits_{i = 1}^{\left| {{V_1}} \right|} {\mathop {\min }\limits_j \;} {D_{ij}} + \frac{1}{{\left| {{V_2}} \right|}}\sum\limits_{j = 1}^{\left| {{V_2}} \right|} {\mathop {\min }\limits_i } \;{D_{ij}} $ |
其中, Dij=‖F1(i)-F2(j)‖, D∈R|V1|×|V2|。
上述距离在物理上表示2个结构中的所有节点到对方结构最近距离的平均值。
本文提出的结构距离计算算法伪代码如下:
算法1 结构距离计算算法
Require:
网络结构图G1(ν1, ε1)和G2(ν2, ε2)
领域等级K
Ensure:
1.V=V1∪V2
2.for vin V do
3.计算数据流连接特征dv-、dv+
4.提取节点特征fv;
5.end for
6.选取关键性节点集合Γ=Γ1∪Γ2;
7.计算Γ对应的相似性矩阵SΓ;
8.[U, Σ, V]=SVD(SΓ$† $);
9.计算相似性矩阵S1和S2;
10.$\mathrm{F}_{1}=\mathrm{S}_{1} \mathrm{U} \Sigma^{\frac{1}{2}}, \mathrm{~F}_{2}=\mathrm{S}_{2} \mathrm{U} \Sigma^{\frac{1}{2}}$
11. ${\rm{ dist }} = \frac{1}{{\left| {{{\rm{V}}_1}} \right|}}\sum\limits_{i = 1}^{\left| {{{\rm{v}}_1}} \right|} {\mathop {\min }\limits_{\rm{j}} } \; {{\rm{D}}_{{\rm{ij}}}} + \frac{1}{{\left| {{{\rm{V}}_2}} \right|}}\sum\limits_{{\rm{j}} = 1}^{\left| {{{\rm{v}}_2}} \right|} {\mathop {\min }\limits_{\rm{i}} \; } {{\rm{D}}_{{\rm{ij}}}}$;
12.return dist
3 多样性解本节主要介绍Diverse M-Best解的选取方法, M-Best问题在本文主要指选取最有潜力的M个结构。
给定一个标量δ, 定义δ-结构如下:
定义1 (δ-结构) 将结构ϕ距离为δ的邻域记为Nδ(ϕ), Nδ(ϕ)即以ϕ为中心、δ为半径的球体, 其在数学形式上表示为{s|Δ[(s, ϕ)≤δ]}。如果一个结构比其邻域Nδ(ϕ)中的其他结构的评价指标都高, 则该结构就是一个δ-结构。
记ρ(ϕ):Ψ→R表示网络结构的评价函数, 其中, ϕ表示结构, Ψ表示结构空间。通常情况下采取的网络结构评价指标就是结构在验证集上的准确率, 优化的直接目的是寻找评价指标最高的网络结构, 将其记为MAP(Maximum A Performance)。
3.1 通常形式考虑到本文的目的是选取多样性且高质量的解, 因此, 采用迭代的方式来解决多样性解的选取问题。假定已经选取了{ϕ1, ϕ2, …, ϕt}共t个解, 则第t+1个解被认为是剩余解中评价指标最高且距离已有解有一定距离的解, 上述寻找方式可以用如下的迭代优化形式表示:
| $ \begin{array}{*{20}{l}} {\mathop {\max }\limits_{{\phi _{t + 1}} \in \Psi } }&{\rho \left( {{\phi _{t + 1}}} \right)}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}}&{{\phi _{t + 1}} \in \overline {{{\cal N}_\delta }} \left( {{\phi _i}} \right),\forall i \in \{ 1,2, \cdots ,t\} } \end{array} $ |
其中, $\overline{\mathcal{N}_{\delta}}\left(\phi_{i}\right)$是集合Nδ(ϕi)的补集。从上式可以看出, 当前寻找的解距离已有解至少有δ的距离。Top M-Best可以看成是Diverse M-Best的一个特例, 当Δ(·, ·)是0-1相似(例如Δ(G1, G2)=1(G1==G2))且δ=0时, Diverse M-Best即为Top M-Best, 迭代优化所寻找的下一个多样性解即为最优解。
3.2 松弛形式通常形式适用于结构和评价指标已知的情况。但有时并不能准确地获取结构和评价指标数值间的关系, 此时需要用到一些近似。为了消除近似带来的误差, 本文将通常形式转变成松弛形式, 如下:
| $ \begin{array}{*{20}{l}} {\mathop {\max }\limits_{{\phi _{t + 1}} \in \psi } \rho \left( {{\phi _{t + 1}}} \right)}\\ {{\rm{ s}}{\rm{. t}}{\rm{. }}{\phi _{t + 1}}{ \notin _p}{{\cal N}_\delta }\left( {{\phi _i}} \right),\forall i \in \{ 1,2, \cdots ,t\} } \end{array} $ |
其中, ∉p表示ϕt+1以概率p不属于邻域
本文探究网络搜索在少量步数情况下的网络性能分布和在充分训练后的网络性能分布之间的关系, 阐述多样性的重要性, 利用Diverse M-Best的方式在分类任务CIFAR10和ImageNet上进行相关的搜索实验, 以呈现多样性搜索的效果, 在此基础上, 对多样性解中的超参数设置进行评估和探讨。
4.1 实验设置本文的多数实验是在计算机视觉领域广泛使用的CIFAR-10数据集上进行, 只有分类实验同时在CIFAR-10和大数据集ImageNet上进行。CIFAR-10包括60 000张尺寸为32×32的图片, 包含10个类别物体, 共50 000张训练集和10 000张测试集。在结构搜索的实验中, 本文提前从训练集中随机选取5 000张图片作为验证集, 用剩余的45 000张图片作为训练集, 所有的图片都经过标准的预处理和增广, 比如减去均值、除以标准差、将图片补成40×40尺寸然后随机截取32×32大小, 最后随机水平翻转图片。
本次实验中的参数设置参考文献[22], 在CIFAR-10上的最大训练步数为600步, 充分训练时在2/3的位置使用辅助头, 辅助头函数的损失权重为0.4, 路径Dropout的概率为0.4, 梯度以5为模长进行截取, 训练过程采用0.025的初始学习率, 学习率按照余弦函数衰减。
4.2 分布探索在神经网络结构搜索中, 研究人员对模型通常只训练有限的步数, 通过有限步数来评估模型, 然后利用验证集上的预测效果选出最好的一个或M个模型再完成充分训练。上述操作的假设条件是在少量步数训练情况下模型的准确率分布和充分训练后的模型准确率分布具有较强的相关性。本次实验共进行5次, 从PNAS空间中随机选取100个模型结构, 然后展示充分训练和少量步数训练下模型准确率分布的关系。
图 3(a)所示为随机选取的100个网络结构在少量步数训练(20步)与充分训练(600步)情况下的准确率相关性, 其中, 每个点表示一个网络结构, 横坐标表示该网络结构在少量训练步数下验证集准确率的排序情况, 纵坐标表示该网络结构经过充分训练后在验证集上准确率的排序情况。图中点的平均线性相关系数为34.7%, 因此, 难以确定在少量训练步数下验证集准确率最高的网络结构在经过充分训练后准确率也是最高。图 3(b)所示为不同的少量训练步数情况下样本排序情况和充分训练后样本排序情况之间的相关性, 从中可以看出, 随着训练步数的增加, 相关性提高, 但即使训练步数达到100步, 相关性也只有0.5左右, 而通常情况下研究人员采取的训练步数都远低于100步。

|
Download:
|
| 图 3 训练步数对实验结果的影响 Fig. 3 The effect of training steps on the experimental results | |
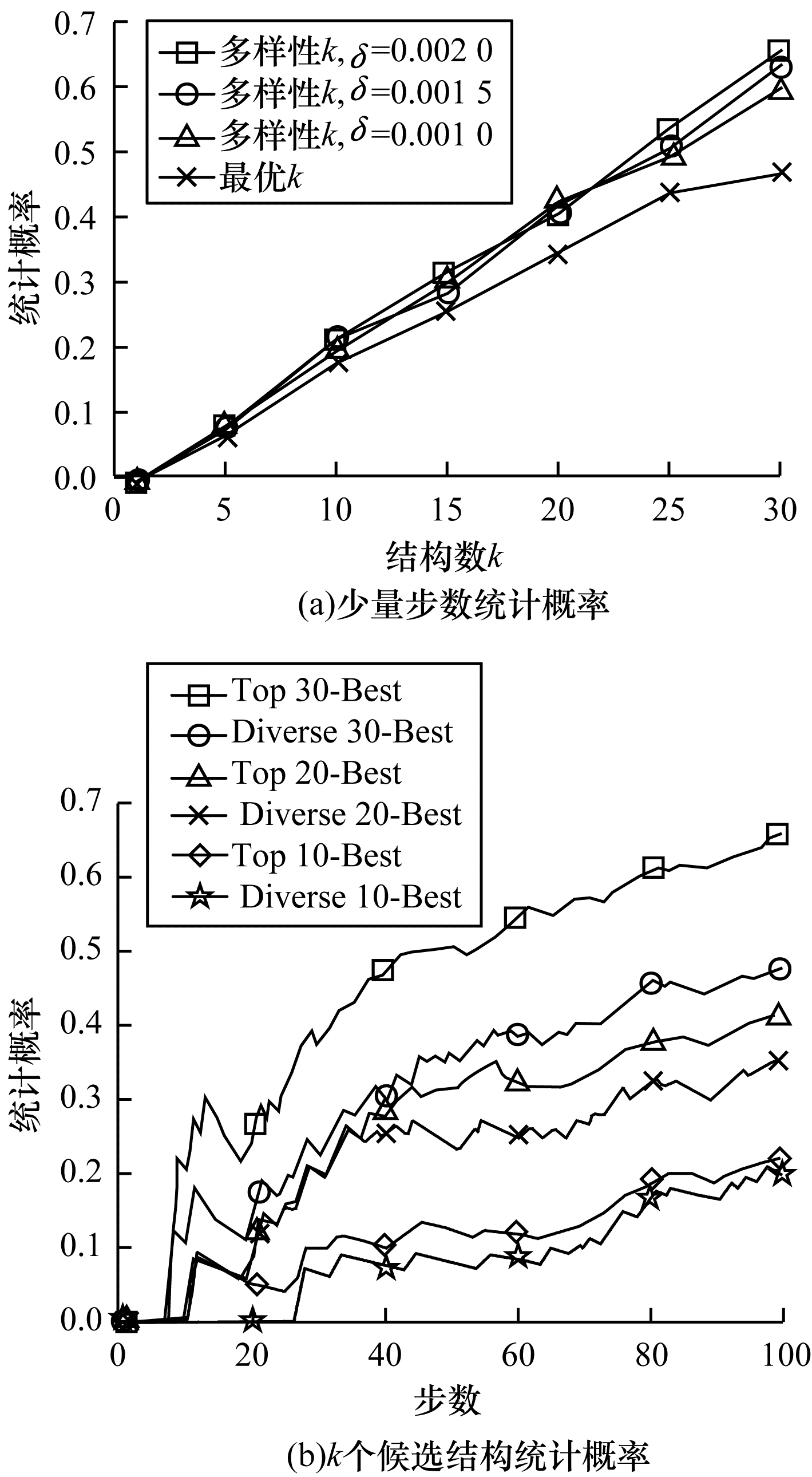
仅通过少量步数(不超过100步)训练时选出真正充分训练后最优结构的统计概率如图 4(a)所示, 从中可以看出, 多样性挑选的方式能够提高选中真正最优网络结构的概率, 多样性的提升值在一定程度上随着挑选个数k的改变而呈上升趋势。在训练不超过某步数的情况下, 从少量训练步数的结构中挑选k个候选结构, 挑中真正充分训练后最优结构的统计概率如图 4(b)所示, 从中可以看出, 在这种情况下, 多样性在一定程度上对选中真正最优结构也起到了概率意义上的提升作用。
|
Download:
|
| 图 4 最优结构统计概率 Fig. 4 Statistical probability of optimal structure | |
多样性除了在已知少量训练步数时提高选中真正最优结构的概率, 也有助于搜索算法获取更优的网络结构。本次实验选取PNAS[4]作为对比算法, 按照PNAS的设置, Divs-PNAS同样采取5个LSTM预测器综合的方法, 结构搜索过程中每一个卷积神经网络只训练20步, 算法搜索的最大模块数量为5个。考虑到计算资源的有限性, 每次取Top 64-Best(Diverse 64-Best), 而非PNAS中取256-Best。由于性能分布采取预测器的方式, 为了避免预测器带来的结果差异, 此处多样性使用放松形式, 放松的概率p固定取0.5。下文结果为重复3次实验的平均结果。
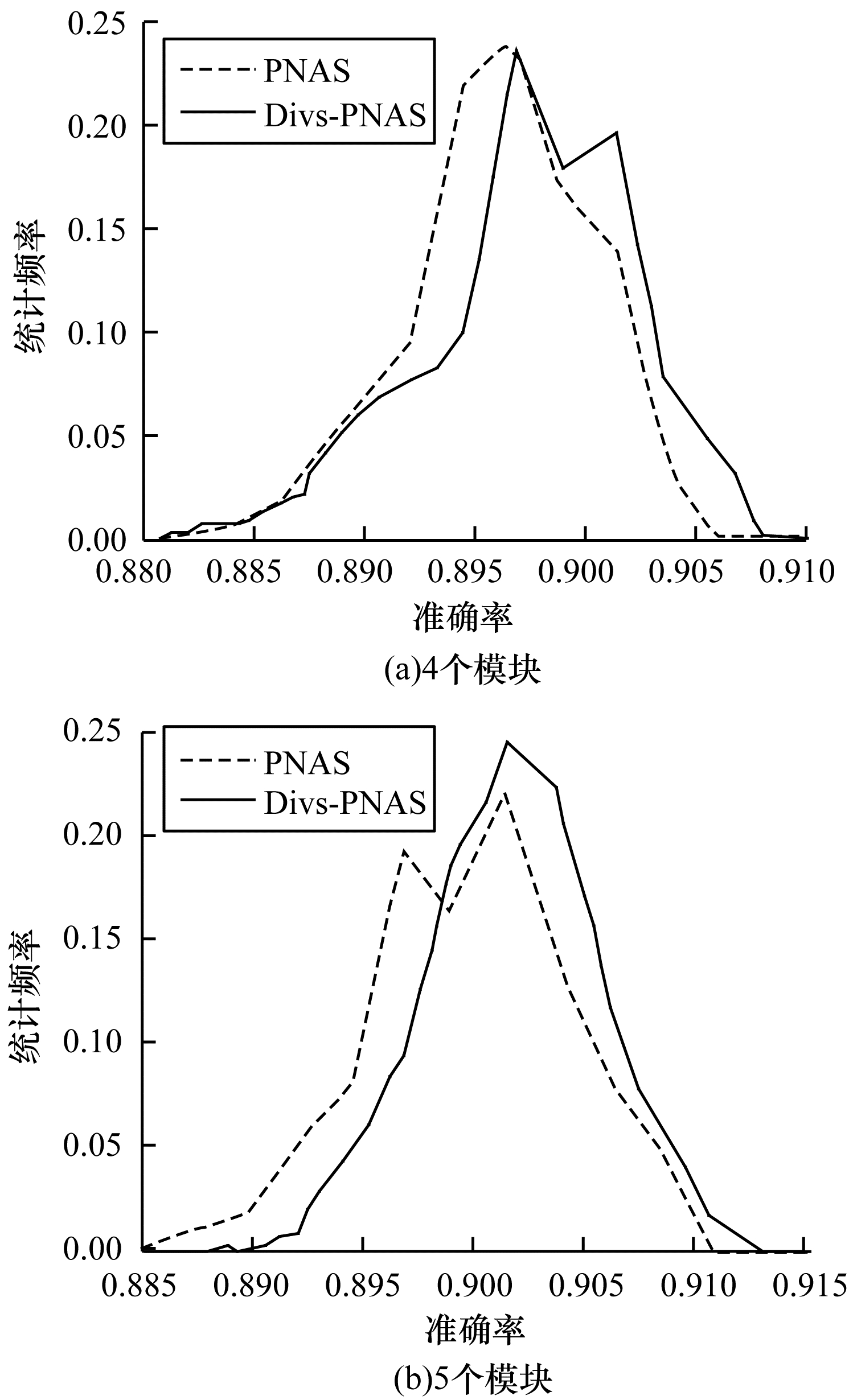
Divs-PNAS和PNAS在4个模块规模的结构单元空间上选出的结构在验证集上的性能统计频率, 以及在5个模块规模的结构单元空间上选出的结构在验证集上的性能统计频率情况如图 5所示。从图 5可以看出, 和PNAS相比, Divs-PNAS能够寻找到更多在验证集上性能更好的模型, 且随着模块数的增加, 该优势变得更加明显。对于这2种方法选取的结构做一个分布均值的T假设检验, 原假设为PNAS挑选出的结构在验证集上的平均性能比Divs-PNAS高。假设检验结果如表 1所示, 从表 1可以看出, 假设检验的p值非常小, 即应该拒绝原假设。通过假设检验可以说明, Divs-PNAS挑选出的结果的平均性能比PNAS更高。
|
Download:
|
| 图 5 Divs-PNAS和PNAS在不同模块数下的性能统计频率 Fig. 5 Performance statistics frequency of Divs-PNAS and PNAS under different number of blocks | |

|
下载CSV 表 1 假设检验的p值 Table 1 p value of hypothesis test |
将Divs-PNAS和PNAS所选出的最终模型结构单元进行对比。使用K=256的Divs-PNAS搜索, 即PNAS中设置256-Best方式。为简单起见, 对搜索出的单元通道数以及堆叠层数不做优化, 而是直接采取PNAS的值进行对比实验。
在CIFAR-10上搜索的不同模块数结构单元实验结果如表 2所示。从表 2可以看出, 在相同的模块数下, 和Top的方式相比, Diverse能够提升搜索性能, 平均错误率下降了9个百分点。
|
下载CSV 表 2 CIFAR-10数据集上的实验结果 Table 2 Experimental results on CIFAR-10 dataset |
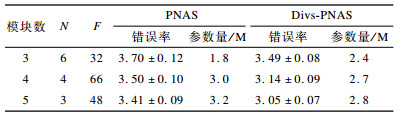
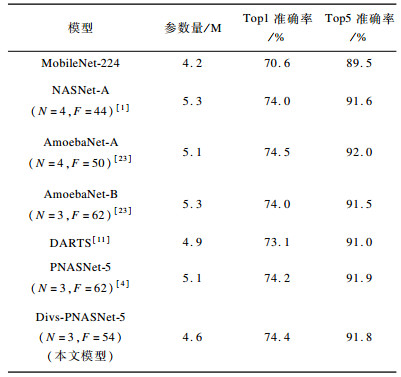
在CIFAR-10上利用Divs-PNAS搜索的最好的5个模块结构为Divs-PNASNet-5, 将该结构单元直接应用到大规模数据集ImageNet分类任务上。按照Mobile Setting的设置, 将输入设置为224×224大小, 实验结果如表 3所示。从表 3可以看出, 和PNASNet-5相比, Divs-PNASNet-5的Top1准确率有轻微提升, Divs-PNASNet-5为74.4%, 而PNASNet-5为74.2%, 但是Top5准确率却下降0.1%。可能有2个原因:一是数据集本身的迁移所致, CIFAR-10上表现更好的模块在ImageNet上不一定就更好; 二是为了便于比较, 对于网络结构参数N和F直接采用的是PNAS的设置参数, 而没有与PNAS一样对N和F做优化挑选。总体而言, Divs-PNASNet-5和PNASNet-5性能相近, 但其参数量更少。
|
下载CSV 表 3 Top1与Top5实验结果 Table 3 Experimental results of Top1 and Top5 |
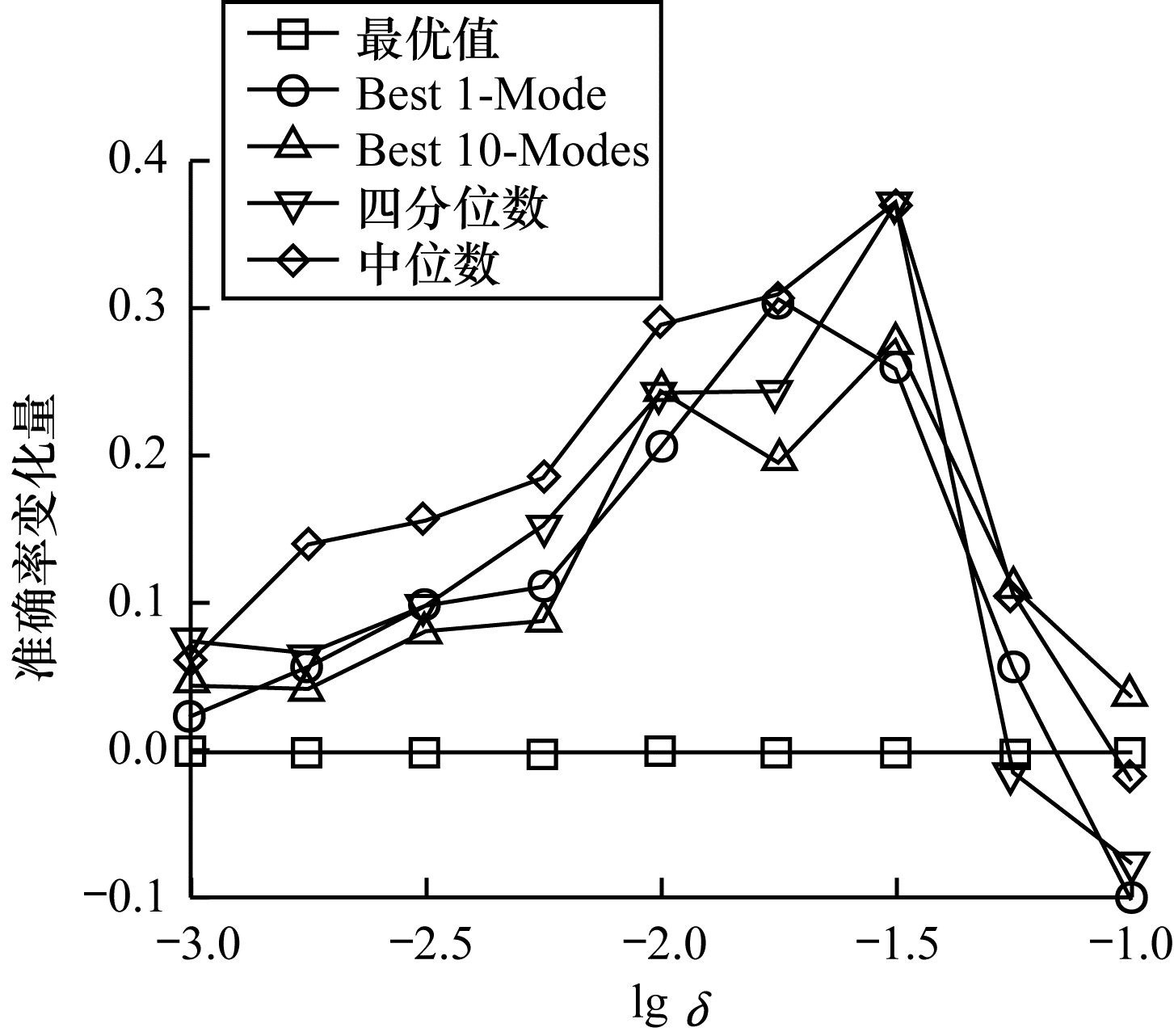
多样性搜索中的一个重要参数就是表征多样性范围的δ值。按照4.3节的设置, 在CIFAR-10上分别运行不同δ值的Divs-PNAS。进行3次实验, δ对准确率变化量的平均影响效果如图 6所示。
|
Download:
|
| 图 6 δ值对搜索结果的影响 Fig. 6 The effect of δ value on search results | |
从图 6可以看出, 随着δ的增加, 不同的统计量都有不同程度的提升。在开始时, 随着δ的增加, 多样性搜索的效果呈现上升的趋势, 但是δ增加到一定程度后, 多样性搜索的效果会出现下降的趋势。主要原因在于, 当δ较小时, δ的增加可以扩大有效的可选取的网络结构范围, 但是, 随着δ的继续增加, 多样性M-Best会选取到更多表现较弱的模型结构, 从而导致整体分布的统计情况下降。在实际中, 合适的δ值应该通过实验来获取。
相对于PNAS等传统方法, 考虑多样性的搜索策略的性能提高主要有2个方面的原因:一是基于图的结构度量方法保证了训练集结构的合理性, 有助于减少训练步数和训练时间, 提高搜索效率; 二是考虑多样性后候选解差异性提高, 避免了相似解带来的局限性, 使候选解中包含了真正意义上的最优解, 提高了解的质量。
5 结束语本文探索少量步数训练和充分训练2种情况下的网络结构性能关系, 在此基础上, 提出一种基于图的网络结构距离度量方法, 同时引入多样性搜索的概念。实验结果表明, 多样性搜索有助于寻找到更优的网络结构。下一步的工作分为2个方向, 一是研究如何动态调整多样性的距离阈值参数δ, 使得多样性搜索更加有效, 二是探索效率更高的节点特征提取方式, 从而提高距离计算的效率以及搜索性能。
| [1] |
ZOPH B, VASUDEVAN V, SHLENS J, et al.Learning transferable architectures for scalable image recognition[EB/OL].[2020-05-20].https://openaccess.thecvf.com/content_cvpr_2018/papers/Zoph_Learning_Transferable_Architectures_CVPR_2018_paper.pdf.
|
| [2] |
PHAM H, GUAN M, ZOPH B, et al.Efficient neural architecture search via parameter sharing[EB/OL].[2020-05-20].https://arxiv.org/abs/1802.03268.
|
| [3] |
CAI Han, CHEN Tianyao, ZHANG Wennan, et al.Efficient architecture search by network transformation[C]//Proceed-ings of the 32nd Conference on Artificial Intelligence.Washington D.C., USA: IEEE Press, 2018: 151-163.
|
| [4] |
LIU C, ZOPH B, SHLENS J, et al.Progressive neural architecture search[EB/OL].[2020-05-20].https://arxiv.org/pdf/1712.00559.pdf.
|
| [5] |
BAKER B, GUPTA O, NAIK N, et al.Designing neural network architectures using reinforcement learning[EB/OL].[2020-05-20].https://arxiv.org/abs/1611.02167.
|
| [6] |
ZHONG Zhao, YAN Junjie, WU Wei, et al.Practical block-wise neural network architecture generation[EB/OL].[2020-05-20].https://arxiv.org/abs/1708.05552.
|
| [7] |
LIU Yong, YAO Xin. A population-based learning algorithm which learns both architectures and weights of neural networks[J]. Chinese Journal of Advanced Software Research, 1996, 3(1): 54-65. |
| [8] |
PIERGIOVANNI A, ANGELOVA A, TOSHEV A, et al.Evolving space-time neural architectures for videos[C]//Proceedings of 2019 IEEE/CVF International Conference on Computer Vision.Washington D.C., USA: IEEE Press, 2019: 16-28.
|
| [9] |
DENG Ningyi, SHEN Zhiqiang, GUO Yuefei. Significance detection based on category prior and deep neural network features[J]. Computer Engineering, 2017, 43(6): 225-229. (in Chinese) 邓凝旖, 沈志强, 郭跃飞. 基于类别先验与深度神经网络特征的显著性检测[J]. 计算机工程, 2017, 43(6): 225-229. |
| [10] |
VAHDAT A, MALLYA A, LIU M Y, et al.UNAS: differentiable architecture search meets reinforcement learning[EB/OL].[2020-05-20].https://arxiv.org/abs/1912.07651.
|
| [11] |
KANDASAMY K, NEISWANGER W, SCHNEIDER J, et al.Neural architecture search with Bayesian optimisa-tion and optimal transport[EB/OL].[2020-05-20].https://arxiv.org/abs/1802.07191.
|
| [12] |
VOGELSTEIN J T, CONROY J M, LYZINSKI V, et al. Fast approximate quadratic programming for graph matching[J]. PLoS One, 2015, 10(4): 1-17. |
| [13] |
SINGH R, XU J, BERGER B. Global alignment of multiple protein interaction networks with application to functional orthology detection[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(35): 12763-12768. DOI:10.1073/pnas.0806627105 |
| [14] |
LIAO C S, LU K, BAYM M, et al. IsoRankN:spectral methods for global alignment of multiple protein networks[J]. Bioinformatics, 2009, 25(12): 1253-1258. |
| [15] |
KOLLIAS G, MOHAMMADI S, GRAMA A. Network Similarity Decomposition(NSD):a fast and scalable approach to network alignment[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(12): 2232-2243. DOI:10.1109/TKDE.2011.174 |
| [16] |
GLIGORIJEVI V, MALOD-DOGNIN N, PRŽULJ N. Fuse:multiple network alignment via data fusion[J]. Bioinformatics, 2016, 32(8): 1195-1203. DOI:10.1093/bioinformatics/btv731 |
| [17] |
BAYATI M, GERRITSEN M, GLEICH D F, et al.Algorithms for large, sparse network alignment problems[C]//Proceedings of 2009 IEEE International Conference on Data Mining.Washington D.C., USA: IEEE Press, 2009: 705-710.
|
| [18] |
KOUTRA D, TONG H H, LUBENSKY D.BIG-ALIGN: fast bipartite graph alignment[C]//Proceedings of 2013 IEEE International Conference on Data Mining.Washington D.C., USA: IEEE Press, 2013: 389-398.
|
| [19] |
BAYATI M, SHAH D, SHARMA M. Maximum weight matching via max-product belief propagation[J]. IEEE Transactions on Information Theory, 2005, 54(3): 1763-1767. |
| [20] |
MALMI E, CHAWLA S, GIONIS A. Lagrangian relaxations for multiple network alignment[J]. Data Mining and Knowledge Discovery, 2017, 31(5): 1331-1358. DOI:10.1007/s10618-017-0505-2 |
| [21] |
ZHANG Si, TONG Hanghang.Final: fast attributed network alignment[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2016: 1224-1237.
|
| [22] |
HEIMANN M, SHEN H M, SAFAVI T, et al.REGAL: representation learning-based graph alignment[EB/OL].[2020-05-20].https://arxiv.org/abs/1802.06257.
|
| [23] |
DRINEAS P, MAHONEY M W.Approximating a gram matrix for improved kernel-based learning[M].Berlin, Germany: Springer, 2005.
|
 2020, Vol. 46
2020, Vol. 46
