随着互联网技术的飞速发展, 很多互联网网站(如阿里巴巴、PaperWeekly等)都面临严重的信息过载问题, 这增加了用户获得有价值信息的难度。优秀的推荐算法能够帮助用户在海量商品中找到自己感兴趣的商品, 对于新进入系统的商品也能实现精准推荐, 因此, 对于推荐算法的研究具有重要意义。
现有的推荐算法可分为基于内容的推荐[1]、协同过滤[2]以及结合这两者的混合算法[3]。基于内容的推荐算法对商品提取特征, 将与已购买商品特征相似的商品推荐给用户。文献[4]使用向量空间模型表示商品特征, 并利用K近邻得到基于内容的支持度, 缓解了冷启动问题, 但特征提取算法仍有改进空间, 而且单独使用基于内容的推荐算法效果较差。在协同过滤算法中, 目前应用最广泛的方法是矩阵分解, 即使用奇异值分解(Singular Value Decomposition, SVD)模型对评分矩阵的缺失值进行填充。SVD++模型[5]引入用户和商品的偏置项并融合了隐反馈信息, timeSVD++模型[6]在此基础上引入时间效应, 这类隐因子模型在国际竞赛中取得了优异成绩并被封装成SVDFeature工具包[7]。概率矩阵分解(Probabilistic Matrix Factorization, PMF)模型[8]引入特征向量的先验分布, 用最大后验概率求解参数。贝叶斯概率矩阵分解模型[9]将PMF中先验分布的超参数视为变量, 对其做马尔科夫链蒙特卡洛(Markov Chain Monte Carlo, MCMC)采样, 避免了调参时复杂的网格搜索。局部低秩矩阵近似模型[10]则将完整矩阵近似成多个可分解的局部低秩矩阵之和。上述矩阵分解模型效果较好, 但都无法解决冷启动问题。混合推荐算法结合了上述两类算法的优势, 是目前的研究趋势。基于栈式降噪自编码器的混合推荐算法[11]使用栈式降噪自编码器抽取用户特征并用于协同过滤。协同主题回归模型(Collaborative Topic Model, CTR)[12]利用潜在狄利克雷分布(Latent Dirichlet Allocation, LDA)[13]算法抽取商品特征并用于协同过滤, 但LDA在文本以外的领域特征提取能力较弱。
上述推荐算法都默认评分矩阵中的缺失值表示用户对该商品不感兴趣, 没有考虑可能是由于地理位置等因素造成该商品未能曝光给用户, 在这种无法区分负样本和未曝光样本的推荐场景下, 直接对完整的矩阵进行操作往往效果不佳。为此, 单类协同过滤算法[14]通过负采样得到负样本, 权重矩阵分解算法[15]对观测值和缺失值采用不同的损失权重, 但这两种算法对曝光因素的处理都不够细致。曝光矩阵分解模型ExpoMF[16]将曝光变量看作隐变量, 使用EM算法对曝光隐变量、曝光先验、用户特征向量和商品特征向量做参数估计, 但破坏了先验和似然的共轭关系, 推断结果较差, 而且无法解决冷启动问题。
另一方面, 深度学习在自然语言处理和计算机视觉等领域应用广泛, 理论上神经网络可拟合任意的连续函数, 表征能力远超线性模型。文献[17]通过引入噪声增加了栈式自编码器的鲁棒性。文献[18]对观测变量和隐变量使用二部图建模, 利用吉布斯采样推断隐变量的后验分布。文献[19]将受限玻尔兹曼机堆叠, 使用逐层贪婪预训练, 得到了更好的特征提取效果。文献[20]将变分推断与深度学习结合提出的变分自编码器(Variational Auto-Encoder, VAE), 具有更好的可解释性, 而且在图像等领域的特征提取任务上表现优异, 也可用于推荐算法。
受此启发, 本文提出基于变分自编码器(Variational Auto-Encoder, VAE)的推荐算法VAHR, 使用MCMC采样保证先验和似然的共轭关系, 设计变分自编码器VAEe对用户曝光向量进行重构, 并通过推断得到的用户特征矩阵、曝光矩阵和评分矩阵训练变分自编码器VAEi, 用于提取新商品的协同隐特征向量进行协同过滤, 从而完成新商品的推荐。
1 相关工作VAHR算法最核心的部分是对曝光隐变量等参数的推断以及变分自编码器的使用, 因此, 本节介绍近似推断和引入了曝光隐变量的ExpoMF模型。
1.1 近似推断贝叶斯推断中的近似推断指对模型参数或隐变量的后验分布做近似的推断, 根据推断结果的确定性可分为随机推断和确定推断, 具体如下:
1) 随机推断中最常见的方法为MCMC采样。该方法先构造一条以真实后验分布为平稳分布和极限分布的马尔科夫链, 随机选取一个参数初始值(即相当于随机选取一个初始分布), 不断按照该马氏链做状态转移, 迭代一定次数后则认为当前采样近似服从真实后验分布。MCMC采样对初始值不敏感, 推断效果较好, 因此, VAHR算法使用MCMC采样中的吉布斯采样做参数推断。
2) 确定推断中最常见的方法为变分推断。通常隐变量后验分布形式复杂, 因此, 本文采用类似变分法的方法寻找一个简单的变分分布作为近似, 通过最大化证据下界(Evidence Lower Bound, ELBO)得到该变分分布。文献[20]提出的变分自编码器使用摊余推断最大化ELBO, 将变分分布看作高斯分布, 由编码器学习均值和协方差矩阵, 再由解码器对输入进行重构。目标函数如式(1)所示:
| $ \begin{array}{*{20}{l}} {L(\phi ,\theta ) = {E_{Z \backsim {Q_\phi }(Z|X)}}[{{\log }_a}{P_\theta }(\mathit{\boldsymbol{X}}|\mathit{\boldsymbol{Z}})] - }\\ { {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{KL}} ({Q_\phi }\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(\mathit{\boldsymbol{Z}}))} \end{array} $ | (1) |
其中, ϕ和θ表示编码器和解码器的网络参数, X表示输入样本, Z表示隐变量, Qϕ(Z|X)表示变分分布。
VAE利用蒙特卡洛方法近似对数似然的期望, 使用重参数化技巧确保梯度顺利传播到编码器的参数。本文提出的VAHR算法使用VAE重构用户的曝光向量和抽取商品的协同隐特征。
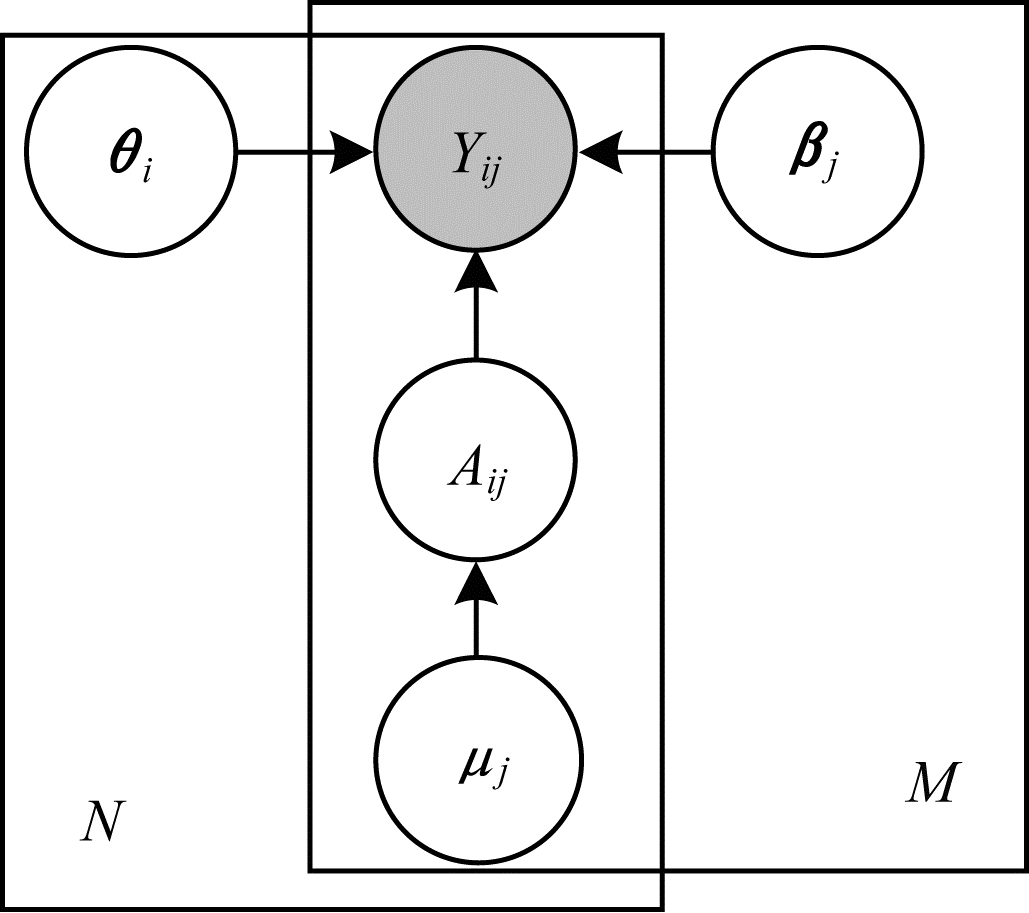
1.2 ExpoMF模型文献[16]提出的ExpoMF模型, 是一种引入曝光隐变量的生成模型。以i表示用户(i=1, 2, …, N), j表示商品(j=1, 2, …, M), 二元的点击变量Yij表示用户i是否点击过商品j, 二元的曝光变量Aij表示商品j是否曝光给用户i, θi和βj表示用户i和商品j的K维特征向量, 对商品j使用统一的曝光先验μj, Yij的生成过程如式(2)所示:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\theta }}_i} \backsim N({\bf{0}},\lambda _\theta ^{ - 1}{I_K})}\\ {{\mathit{\boldsymbol{\beta }}_j} \backsim N({\bf{0}},\lambda _\beta ^{ - 1}{I_K})}\\ {{A_{ij}} \backsim {\rm{Bernoulli}} ({\mu _j})}\\ {\left\{ {\begin{array}{*{20}{l}} {{Y_{ij}} \backsim N(\mathit{\boldsymbol{\theta }}_i^{\rm{T}}{\mathit{\boldsymbol{\beta }}_j},\lambda _y^{ - 1}),{A_{ij}} = 1}\\ {{Y_{ij}} = 0,{A_{ij}} = 0} \end{array}} \right.} \end{array} $ | (2) |
其中, λθ、λβ和λy为超参数, IK为K维单位矩阵。ExpoMF的概率图模型如图 1所示。
|
Download:
|
| 图 1 ExpoMF的概率图模型 Fig. 1 Probability graph model of ExpoMF | |
ExpoMF使用EM算法在有隐变量A的情况下做θ、β和μ的参数估计, 其中θ、β和μ表示相应参数对应的矩阵或向量。
在E步计算Aij的期望
| $ \begin{array}{l} {{\tilde P}_{ij}} = E({A_{ij}}|{\mathit{\boldsymbol{\theta }}_i},{\mathit{\boldsymbol{\beta }}_j},{\mu _j},{Y_{ij}} = 0) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mu _j} \cdot N(0|\mathit{\boldsymbol{\theta }}_i^{\rm{T}}{\mathit{\boldsymbol{\beta }}_j},\lambda _y^{ - 1})}}{{{\mu _j} \cdot N(0|\mathit{\boldsymbol{\theta }}_i^{\rm{T}}{\mathit{\boldsymbol{\beta }}_j},\lambda _y^{ - 1}) + (1 - {\mu _j})}} \end{array} $ | (3) |
在M步计算μ、θ和β的后验。求解θi时, 虽然θi的先验分布为高斯分布, 但由于
在EM算法迭代较多次数后认为模型参数已经收敛, 得到最终参数。在预测阶段, 根据ExpoMF的生成过程, 预测结果的期望如式(4)所示:
| $ {\hat Y_{ij}} = {\mu _j} \cdot \mathit{\boldsymbol{\theta }}_i^{\rm{T}}{\mathit{\boldsymbol{\beta }}_j} $ | (4) |
本文VAHR算法使用吉布斯采样, 将前一次迭代结果作为先验, 推断效果更好, 而且ExpoMF无法解决新商品的冷启动问题, 对曝光信息的使用也存在缺陷, VAHR对此也加以改进。
2 VAHR算法VAHR算法结构分为3层, 即推断层、VAE层和预测层。该算法在推断层推断曝光矩阵、曝光先验向量、用户特征矩阵和商品特征矩阵4组参数, 在VAE层训练2个VAE, 分别用于重构用户曝光向量和抽取商品协同隐特征, 在预测层做用户对旧商品和新商品点击情况的预测。其中:商品的协同隐特征向量指可以用于协同过滤的特征向量; 商品的隐特征向量指用特征提取模型(如VAE)提取出的特征向量, 不能很好地用于协同过滤; 商品的特征向量指经特征工程得到的商品辅助信息, 作为VAE的输入。在不会产生歧义时, 为叙述简便, 本文不对其进行严格区分。
2.1 推断层VAHR算法使用吉布斯采样做A、μ、θ和β的推断。根据吉布斯采样的收敛性, 可以随机初始化上述4组参数, 但为了加快收敛速度, 4组参数的初始化方式见3.4.1节。首先对A进行采样, Yij=1时Aij一定为1, Yij=0时Aij的完整条件概率见式(3), 可从式(5)的伯努利分布中采样出Aij。
| $ {A_{ij}} \backsim {\rm{ Bernoulli }}(\widetilde {{P_{ij}}}) $ | (5) |
θi和βj完整条件概率的计算方式类似, 下面以θi举例说明。根据D分离方法, θi和θ
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\theta }}_i} \backsim P({\mathit{\boldsymbol{\theta }}_i}|\mathit{\boldsymbol{\beta }},\mathit{\boldsymbol{A}},\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{\mu }},{\mathit{\boldsymbol{\theta }}_{\neg i}}) = P({\mathit{\boldsymbol{\theta }}_i}|\mathit{\boldsymbol{\beta }},{\mathit{\boldsymbol{A}}_i},{\mathit{\boldsymbol{Y}}_i},\mathit{\boldsymbol{\mu }}) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P({\mathit{\boldsymbol{\theta }}_i}|\mathit{\boldsymbol{\beta }},{\mathit{\boldsymbol{A}}_i},{\mathit{\boldsymbol{Y}}_i})} \end{array} $ | (6) |
由于此时β、A和Y为已知值, 因此式(6)正比于式(7)左边的联合概率:
| $ \begin{array}{*{20}{l}} {P({\mathit{\boldsymbol{\theta }}_i},\mathit{\boldsymbol{\beta }},{\mathit{\boldsymbol{A}}_i},{\mathit{\boldsymbol{Y}}_i}) = P({\mathit{\boldsymbol{\theta }}_i})P({\mathit{\boldsymbol{Y}}_i}|{\mathit{\boldsymbol{\theta }}_i},\mathit{\boldsymbol{\beta }},{\mathit{\boldsymbol{A}}_i})P(\mathit{\boldsymbol{\beta }})P({\mathit{\boldsymbol{A}}_i}) \propto }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P({\mathit{\boldsymbol{\theta }}_i})P({\mathit{\boldsymbol{Y}}_i}|{\mathit{\boldsymbol{\theta }}_i},\mathit{\boldsymbol{\beta }},{\mathit{\boldsymbol{A}}_i})} \end{array} $ | (7) |
当Aij=0时, P(Yij|θi, βj, Aij)=1;当Aij=1时, P(Yij|θi, βj, Aij)为高斯分布, 而且初始的P(θi)为高斯分布。根据高斯相乘引理和数学归纳法可知, 可实现以前一次迭代得到的高斯分布作为先验来进行本次迭代, 得到更精准的推断, 如式(8)所示:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + {\lambda _y}\sum\limits_{j = 1}^M {{A_{ij}}} ({\mathit{\boldsymbol{\beta }}_j}\mathit{\boldsymbol{\beta }}_j^{\rm{T}})}\\ {{\mathit{\boldsymbol{\mu }}^*} = {{[{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}]}^{ - 1}}[\mathit{\boldsymbol{ \boldsymbol{\varLambda} \mu }} + {\mathit{\boldsymbol{\lambda }}_y}\sum\limits_{j = 1}^M {({A_{ij}}{Y_{ij}})} {\mathit{\boldsymbol{\beta }}_j}]}\\ {{\mathit{\boldsymbol{\theta }}_i} \backsim N({\mathit{\boldsymbol{\theta }}_i}|{\mathit{\boldsymbol{\mu }}^*},{{[{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}]}^{ - 1}})} \end{array} $ | (8) |
其中, μ和Λ为前一次迭代得到的高斯分布的均值向量和协方差矩阵的逆矩阵, μ*和Λ*为本次迭代得到的高斯分布的均值向量和协方差矩阵的逆矩阵。
对于μj, 根据D分离方法, 在给定Aj的条件下, μj与其他所有参数独立, μj仅与Aj有关(如式(9)所示), 指定μj服从Beta分布, 设先验为Beta(α1, α2), 根据Beta分布与二项分布的共轭关系可以直接得到μj的后验分布(如式(10)所示), 由此可将前一次迭代得到的Beta分布作为先验来进行本次迭代。
| $ {{\mu _j} \backsim P({\mu _j}|\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\beta }},\mathit{\boldsymbol{A}},\mathit{\boldsymbol{Y}},{\mu _{\neg j}}) = P({\mu _j}|{\mathit{\boldsymbol{A}}_j})} $ | (9) |
| $ {{\mu _j} \backsim {\rm{Beta}} \left( {{\alpha _1} + \sum\limits_{i = 1}^N {{A_{ij}}} ,{\alpha _2} + N - \sum\limits_{i = 1}^N {{A_{ij}}} } \right)} $ | (10) |
使用数学计算库(如numpy)实现μ的采样需要较大计算量, 而在现实的推荐场景中, 用户数N往往非常巨大, 根据Beta分布的特性, 其概率密度函数几乎完全集中于尖锐的一点, 该尖点概率密度极大, 其余点的概率密度接近为0, 并且形状参数越大此特性越明显。为了简化运算, 可以选择不从式(10)分布中采样, 而是指定μj为式(10)Beta分布的众数, 因为使用采样方式得到的样本一定会落在众数附近极狭小的区间内, 2种方法对后面其他3组参数的采样几乎没有差别。众数计算公式如式(11)所示:
| $ {\mu _j} = \frac{{{\alpha _1} + \sum\limits_{i = 1}^N {{\mathit{\boldsymbol{A}}_{ij}}} - 1}}{{{\alpha _2} + {\alpha _2} + N - 2}} $ | (11) |
按照以上顺序迭代采样A、θ、β和μ, 在迭代较多次数后, 认为4组参数收敛到真实的后验分布。吉布斯采样效果较好, 缺点是计算量过大, 其中矩阵求逆的时间复杂度高达O(K3), 对4组参数采样一次的时间复杂度为O(MN(K2+K+1)+(M+N)(K3+K2))。但笔者发现在采样过程中, 曝光矩阵的各元素之间、用户与用户的特征向量之间、商品与商品的特征向量之间和商品与商品的曝光先验之间是各自相互独立的, 因此, 本文对4组参数进行组内并行、组间串行的吉布斯采样。采样A、β和μ时, 对商品集分组, 每组商品放到不同CPU内核上并行; 采样θ时, 对用户集分组, 每组用户放到不同CPU内核上并行。一般来说并行的效率提升倍数与设定的内核数近似呈正比, 但不宜过大, 否则会导致内核间的数据交换耗费过多时间, 每个内核上的利用率不足, 反而降低效率。选择恰当的内核数和分组尺寸需要反复尝试, 具体参数设定见本文实验部分。
2.2 VAE层 2.2.1 用户曝光信息重构ExpoMF在预测时直接使用推断得到的曝光先验μj, 但μj仅反映商品j的热度, 不能具体到某用户, 而ExpoMF中的
| $ {\log _a}{P_\theta }({\mathit{\boldsymbol{\tilde P}}_i}|{\mathit{\boldsymbol{z}}_i}) = - \sum\limits_{j = 1}^M {\frac{{{\lambda _{\rm{e}}}}}{2}} {({\tilde P_{ij}} - {f_\theta }{({\mathit{\boldsymbol{z}}_i})_j})^2} $ | (12) |
其中, fθ为VAEe解码器的函数形式, zi为用户i曝光向量的隐特征, fθ(zi)为VAEe的重构结果, λe为VAEe解码器高斯分布的协方差矩阵系数的倒数。由于Aij为离散值0和1, 因此在解码器部分使用逻辑似然, 此时对数似然等效于交叉熵损失, 如式(13)所示。此外, 对于离散的二元特征也可以选择多项式似然。
| $ \begin{array}{*{20}{l}} {{{\log }_a}{P_\theta }({A_i}|{\mathit{\boldsymbol{z}}_i}) = - \sum\limits_{j = 1}^M {{A_{ij}}} \ln {f_\theta }{{({\mathit{\boldsymbol{z}}_i})}_j} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 - {A_{ij}})\ln (1 - {f_\theta }{{({\mathit{\boldsymbol{z}}_i})}_j})} \end{array} $ | (13) |
为解决新商品的冷启动问题, 使用用户特征矩阵θ、曝光矩阵A和点击矩阵Y训练一个提取商品协同隐特征的VAE, 称之为VAEi。同样地, 对于连续的特征使用高斯似然, 对于离散的二元特征使用逻辑似然。将协同过滤的损失、VAEi的损失以及网络参数正则化项三者综合, 得到完整目标函数, 如式(14)所示, 然后使用梯度上升优化VAEi的网络参数。
| $ \begin{array}{*{20}{l}} {L = {E_{Z \backsim Q(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})}}\left[ { - \frac{{{\lambda _y}}}{2}\sum\limits_{i,j} {{A_{ij}}} {{({Y_{ij}} - \mathit{\boldsymbol{\theta }}_i^{\rm{T}}{z_j})}^2}} \right] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {E_{Z \backsim Q(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})}}\ln P(\mathit{\boldsymbol{X}}|\mathit{\boldsymbol{Z}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{KL}}(Q\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(\mathit{\boldsymbol{Z}})) - \frac{{{\lambda _{\rm{W}}}}}{2}\left\| \mathit{\boldsymbol{W}} \right\|_{\rm{F}}^2} \end{array} $ | (14) |
在式(14)中, X为商品的特征矩阵(辅助信息), Z为商品对应的协同隐特征矩阵, W为VAEi的网络参数矩阵, λW和λy为超参数, 先验分布P(Z)一般选择标准高斯分布。由于VAEi提取出的特征向量服从高斯分布, 因此对协同过滤损失使用期望形式表示。可以把式(14)的第2项和第3项之和视为VAEi的目标函数ELBO1, 也可以把第2项视为样本重构误差的期望, 把第3项看做分布正则化项。具体地, 当第2项很大即重构误差很小时, Q(Z|X)很复杂, 可以对商品进行精准的重构, 但此时它与P(Z)的KL散度也很大, ELBO1不会因为重构误差小而变得很大, 当第2项很小时同理。因此, 第3项KL散度对最大化ELBO1起到了正则作用, 既不会得到过于简单但重构性能过差的VAEi, 又不会得到过于复杂的VAEi, 而是在两者之间进行权衡。
以上为式(14)损失函数角度(损失函数之和)的解释, 此外, 笔者还发现了其概率角度解释。在VAE层, Y、X和θ为已知值, 本文构造P(Y, X, θ)的证据下界ELBO2, 如式(15)所示:
| $ \begin{array}{l} {\rm{ELB}}{{\rm{O}}_2} = {\log _a}P(\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\rm{KL}}(Q\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }})) = }\\ {{E_{Z \backsim Q(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})}}{{\log }_a}P(\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}|\mathit{\boldsymbol{Z}}) - }\\ {{\rm{KL}}(Q\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(\mathit{\boldsymbol{Z}}))} \end{array} \end{array} $ | (15) |
笔者希望寻找一个变分分布Q(Z|X), 使其尽量接近真实后验分布P(Z|Y, X, θ), 因此, 通过最大化ELBO2来达到这一目的, 巧合的是, 最大化带有网络参数正则化项的ELBO2与最大化式(14)是完全等价的, 如式(16)所示:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{E_{Z \backsim Q(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})}}{{\log }_a}P(\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{X}},\mathit{\boldsymbol{\theta }}|\mathit{\boldsymbol{Z}}) - }\\ {{\rm{KL}}(Q\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(\mathit{\boldsymbol{Z}})) = } \end{array}\\ \begin{array}{*{20}{l}} {{E_{Z \backsim Q(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})}}{{\log }_a}[P(\mathit{\boldsymbol{\theta }})P(\mathit{\boldsymbol{Y}}|\mathit{\boldsymbol{Z}},\mathit{\boldsymbol{\theta }})P(\mathit{\boldsymbol{X}}|\mathit{\boldsymbol{Z}})] - }\\ {{\rm{KL}}(Q\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(\mathit{\boldsymbol{Z}})) = } \end{array}\\ \begin{array}{*{20}{l}} {{E_{Z \backsim Q(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})}}[{{\log }_a}P(\mathit{\boldsymbol{Y}}|\mathit{\boldsymbol{Z}},\mathit{\boldsymbol{\theta }}) + {{\log }_a}P(\mathit{\boldsymbol{X}}|\mathit{\boldsymbol{Z}})] - }\\ {{\rm{KL}}(Q\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(Z)) + {\rm const}} \end{array} \end{array} $ | (16) |
协同主题回归(CTR)模型[12]、协同变分自编码器(CVAE)[21]和协同深度学习模型(CDL)[22]都将特征提取算法与协同过滤结合, 使用了类似形式的损失函数, 但它们都只有损失函数角度的解释, 而没有概率角度解释。其中, CVAE使用VAE学习商品的隐特征矩阵Z, 加上弥补项ε得到协同隐特征矩阵V, 用U和V做协同过滤, 训练时对协同过滤参数(U和V)与VAE的网络参数使用块坐标上升交替优化, 损失函数如式(17)所示:
| $ \begin{array}{*{20}{l}} {L = {E_{Z \backsim Q(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})}}{{\log }_a}P(\mathit{\boldsymbol{Y}},\mathit{\boldsymbol{X}},\mathit{\boldsymbol{U}},\mathit{\boldsymbol{V}}|\mathit{\boldsymbol{Z}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{KL}}(Q\left. {(\mathit{\boldsymbol{Z}}|\mathit{\boldsymbol{X}})} \right\|P(\mathit{\boldsymbol{Z}}))} \end{array} $ | (17) |
由于P(Y, X, θ|Z)包含了未知参数U和V, 因此无法解释成似然, 式(17)不可看作ELBO, 破坏了概率角度的可解释性, 只能从损失函数的角度进行解释。此外, 以上4种模型均没有考虑曝光度的问题, 只是对缺失值的损失采用较低权重, 对观测值的损失采用较高权重, 因此, 对旧商品的推荐(in-matrix)效果较差。而对于新商品的推荐(out-of-matrix), 由于新商品弥补项为0, 上述模型仅用LDA、VAE或SDAE学习出了商品的隐特征而不是协同隐特征, 无法有效地用于协同过滤, 因此, 推荐效果不如利用VAE直接学习协同隐特征的VAHR算法。
为保证目标函数可计算, 与VAE相同, 本文使用蒙特卡洛方法对Q(Z|X)采样L个Z来得到损失函数前两项期望的近似; 为保证梯度的顺利传播, 使用重参数化技术模拟对Z的采样; 为防止KL坍塌, 使用KL退火[23]在KL散度前添加系数并在训练初期使其为0, 在训练前中期让其逐渐增加至1以保证VAE的学习效果; 为了加快VAE的收敛速度, 先用特征矩阵(辅助信息)X对VAE单独进行预训练, 然后与协同过滤部分整合进行微调。
2.3 预测层得到用户特征矩阵θ∈
在预测用户i对旧商品j的点击情况时, 使用VAEe对Ai重构得到Ei, 预测结果如式(18)所示:
| $ {\hat Y_{ij}} = {E_{ij}} \cdot \mathit{\boldsymbol{\theta }}_i^{\rm{T}}{\mathit{\boldsymbol{\beta }}_j} $ | (18) |
但式(18)不是在所有推荐场景都表现良好, 考虑以下两个例子:在餐厅的推荐场景下, 曝光因素体现为地理位置, 由于上海的用户很难去北京的餐厅, 因此预测时应考虑曝光变量的制约, 如式(18)所示; 在电影网站的推荐场景下, 曝光因素可以理解为英语地区的用户收到英语电影推荐较多, 由于是网上观影, 因此预测时不应受曝光变量的制约, 如式(19)所示。在不同的推荐场景下应该选择相应的in-matrix预测公式。
| $ {\hat Y_{ij}} = \mathit{\boldsymbol{\theta }}_i^{\rm{T}}{\mathit{\boldsymbol{\beta }}_j} $ | (19) |
在预测用户i对新商品j的点击情况时, 先用VAEi提取新商品的协同隐特征, 由于无法通过推断得知新商品的曝光情况, 因此预测结果如式(20)所示:
| $ {\tilde Y_{ij}} = \mathit{\boldsymbol{\theta }}_i^{\rm{T}}{\mu _\phi }({\mathit{\boldsymbol{x}}_j}) $ | (20) |
其中, xj表示新商品j的特征向量(辅助信息), μϕ表示VAEi编码器的均值网络, μϕ(xj)表示该网络的输出。
2.4 算法描述VAHR算法的具体步骤如下:
输入 点击矩阵Y∈
输出 in-matrix的预测矩阵
步骤1 初始化4组变量θ∈
步骤2 采样A。若Yij=1, 则Aij=1;若Yij=0, 则根据式(5)并行采样Aij。
步骤3 采样θ。对于每个用户i=1, 2, …, N, 根据式(8)并行采样θi。
步骤4 采样β。对于每个商品j=1, 2, …, M, 类似式(8)并行采样βj。
步骤5 采样μ。对于每个商品j=1, 2, …, M, 根据式(11)更新μj。
步骤6 在迭代次数达到预设值时执行步骤7, 否则返回执行步骤2~步骤5。
步骤7 使用A训练VAEe并得到重构结果E∈
步骤8 将X送入VAEi, 取VAEi均值网络的输出, 得到新商品协同隐特征矩阵μφ(X)∈
步骤9 根据式(18)或式(19)得到in-matrix预测矩阵
VAHR算法引入曝光隐变量并使用精准的参数先验, 通过步骤1~步骤6推断出更准确的参数, 这些参数是在各种场景下能取得高推荐质量的基础。在不应受曝光制约的in-matrix场景下, 直接用内积作为预测结果, 虽然预测结果中没有体现曝光信息, 但前面推断层得到的准确参数使得在该场景下可以得到更好的推荐效果。在应受曝光制约的in-matrix场景下, 将曝光预测值与内积相乘得到预测结果, 由于曝光预测值是用VAEe对用户曝光向量重构得到的, 而不是直接使用推断得出的结果, 因此推荐效果更好。在out-of-matrix场景下, 将曝光信息与VAE结合训练出VAEi, 用以提取新商品的协同特征, 可以很好地解决冷启动问题。
3 实验结果与分析本文使用2个真实世界数据集citeulike-a和citeulike-t进行实验, 并将VAHR算法与多个经典算法进行对比, 以证明其有效性。
3.1 实验数据本文实验选用的数据集为推荐系统领域常用的公开数据集citeulike-a和citeulike-t, 包含英文论文网站CiteULike中的一些用户索引与用户看过的文章索引, citeulike-a包含5 551名用户与16 980篇文章, 共204 986个用户-文章点对, 其中看过的总文章数少于10的用户已经被剔除, 经计算该数据集的稀疏度为99.78%, 即该数据集构成的用户-文章点击矩阵中99.78%的元素为0, 其余元素为1。citeulike-t比第1个数据集更大且稀疏程度更高, 其包含7 947名用户与25 975篇文章, 共134 860个用户-文章点对, 其中看过的总文章数少于3篇的用户已经被剔除, 稀疏度为99.93%。2个数据集均通过独立采样得到。
数据集中的每篇文章都包含标题与摘要, 为得到变分自编码器的输入商品特征同时保证实验的公平性与客观性, 本文对数据采用与基准算法相同的处理方式。首先将标题和摘要连接到一起, 然后将没有实际意义的停用词去除, 使用TF-IDF对所有词进行计算, 根据TF-IDF值得到词汇表。citeulike-a的词汇表尺寸为8 000, citeulike-t的词汇表尺寸为20 000, 对每篇文章都用一个词袋直方图向量表示, 向量的维度即词汇表尺寸, 分别进行向量堆叠得到2个数据集对应的矩阵, 然后对这两个矩阵进行归一化, 即对于每个词, 将它出现最多的文章中该词所对应的维度归一化为1, 而对于其余文章, 该维度都要除以其最大出现次数。
3.2 评估指标本文使用召回率衡量推荐效果。召回率等于测试集中真正例的数量除以正例的数量, 即某用户喜欢的商品中被推荐系统命中的商品比例。一般用recall@M表示推荐列表尺寸为M时的召回率, 如式(21)所示:
| $ {\rm{recall@}}{\kern 1pt} M = \frac{{{\rm{ hit}}{{\rm{s}}_M}}}{{{\rm{ testse}}{{\rm{t}}_{\rm{u}}}}} $ | (21) |
其中, hitsM表示推荐M个商品时系统命中的数量, testsetu表示用户u标注过的商品数量, 同时也是系统命中的理论最大值。因为测试集中有些用户的文章数为0, 所以最终的召回率结果取测试集中所有文章数不为0用户召回率的平均值。
3.3 对比算法在in-matrix和out-of-matrix的实验中, 本文选择以下算法进行对比:
1) CTR算法[12]:将协同过滤与特征提取模型结合的推荐算法, 凭借LDA的优越性能, 文本推荐效果较好。
2) CDL算法[22]:将CTR算法中的LDA改进成栈式降噪自编码器(SDAE)。
3) CVAE算法[21]:将协同过滤与变分自编码器结合的模型。
4) ExpoMF算法[16]:引入曝光隐变量的生成模型, 使用EM算法估计模型参数。
5) ACF算法[24]:使用自编码器做特征提取再做协同过滤, 本文在冷启动的实验中以此作为对比算法。
6) LDA算法[13]:使用LDA提取商品特征, 再用K近邻算法完成推荐, 属于基于内容的推荐算法。
7) VAHR算法:考虑曝光隐变量, 使用VAE处理曝光信息并解决了商品的冷启动问题。
3.4 实验设定与结果分析在做in-matrix推荐时对CTR、CDL、CVAE、ExpoMF与VAHR进行比较, 在做out-of-matrix推荐时考虑到本文实验选择的数据集是文本, 因此, 选择对LDA、CTR、ACF与VAHR做纵向比较, 最后选择VAHR的不同超参数做横向比较。
3.4.1 参数设定虽然吉布斯采样理论上一定会收敛, 但为加快收敛速度, 采用以下参数初始化方式。曝光矩阵A的初始状态对收敛速度至关重要, 但由于在VAHR中A是第一个被采样的参数, 因此将其所有元素置0。对于θ和β, 考虑到citeulike-a和citeulike-t数据集的观测值是二元的, 用户和商品的隐特征向量一定在零向量附近, 因此此处使用均值为零向量、协方差矩阵分别为σθ2I和σβ2I的高斯分布对它们初始化, 其中, σθ和σβ设为0.1。对于曝光先验矩阵μ, 指定其服从Beta分布并使用点击矩阵Y初始化, 如式(22)所示, 即认为若某文章j被标注的次数越多, 该文章热度越高, 所对应的μj越大。
| $ {\mu _j} \backsim {\rm{Beta}} \left( {\sum\limits_{i = 1}^N {{Y_{ij}}} ,N - \sum\limits_{i = 1}^N {{Y_{ij}}} } \right) $ | (22) |
超参数设定如下:VAEe编码器的输入层节点数为商品数M, 第1层隐藏层节点数为500, 输出层节点数为200, VAEi编码器的输入层节点数为8 000, 第1层隐藏层节点数为200, 输出层节点数为特征向量维度K, 2个VAE的解码器和编码器结构均对称, 高斯重构分布的协方差矩阵均为σ2I, 其中, σ=0.1, 在2个VAE的全部6个神经网络中使用批量归一化和随机失活, 随机失活的比例为0.1, 学习率为0.01, 正则化系数λw=0.001, λy=0.1, 在训练集上的迭代次数均为500次。文献[21]指出, 当随机梯度下降的批尺寸B足够大时, VAE中的采样数L可设为1, 本文将B设为128。VAHR的超参数相比CVAE和CDL要少一些, 因为VAHR将隐变量推断出来再做协同过滤, 而不是对观测值和缺失值直接使用不同的权重(如CVAE令观测值的权重a=1, 令缺失值的权重b=0.01), 由于它们含有商品隐特征向量的弥补项, 因此还要设定λV来对弥补项正则化。使用机器学习库scikit-learn中的joblib模块实现吉布斯采样的并行, 商品集的分组尺寸为2 000, 用户集的分组尺寸为500, joblib中的并行内核数n_jobs为8。对于KL退火, 让KL散度前的系数从0开始线性增长, 如果增长速度较快则系数为1后的迭代次数相应较少, 网络收敛速度更快, 因此, 本文选择让其在第100次训练集迭代时达到1, 通过KL退火解决KL坍塌问题[24]。
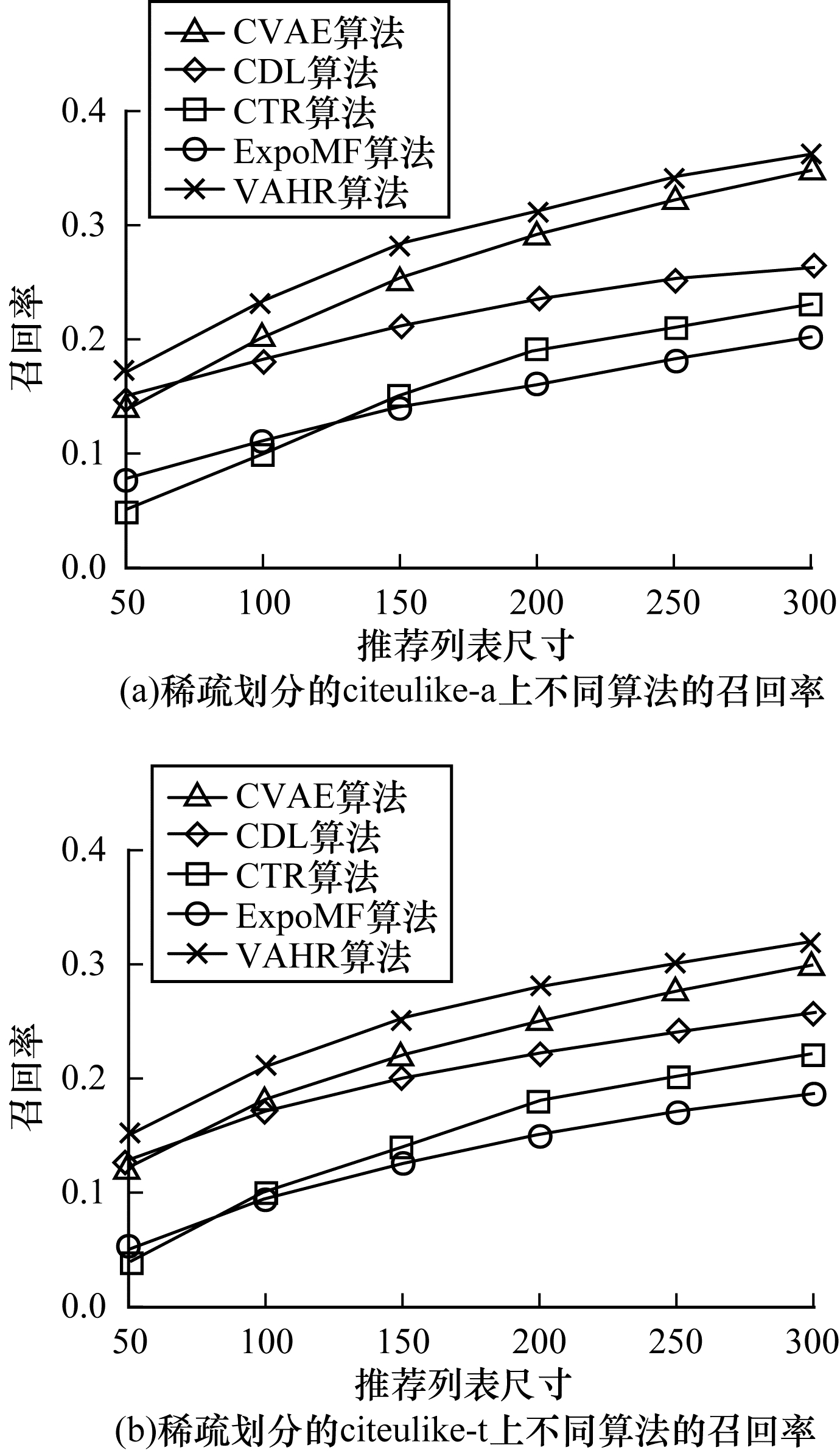
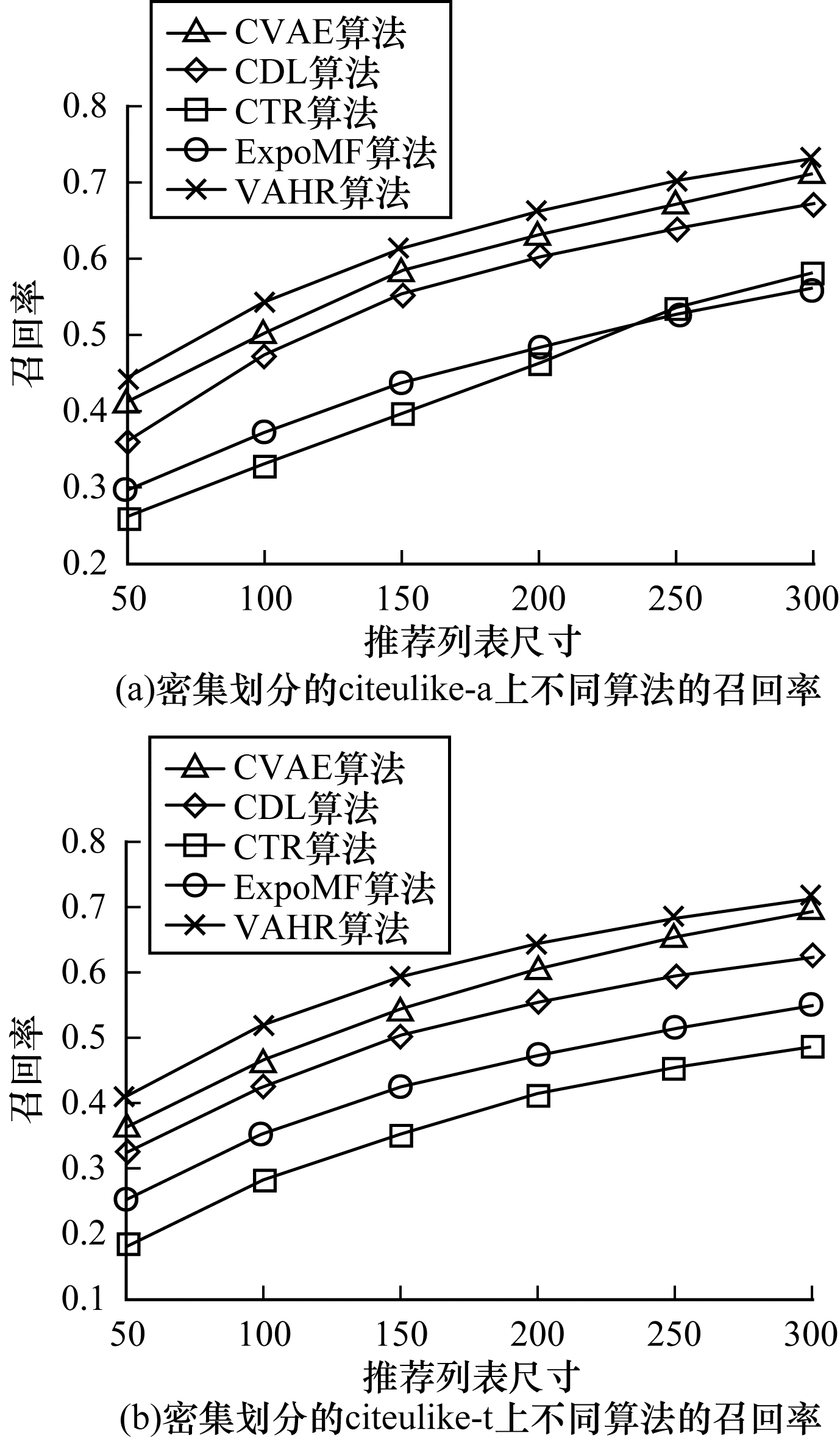
3.4.2 in-matrix推荐在in-matrix推荐中, 划分训练集和测试集时将citeulike-a和citeulike-t分成稀疏和密集2种情况:稀疏情况下对每个用户随机选出1篇已标注的文章放入训练集, 将该用户的剩余文章放入测试集; 密集情况下对每个用户随机选出10篇文章放入训练集, 将剩余文章放入测试集, 共得到4组训练集和测试集。特征向量的维度K=50, 推荐列表尺寸分别取50、100、150、200、250和300, 取第100次吉布斯采样的迭代结果, 稀疏划分情况下的实验结果如图 2所示, 密集划分情况下的实验结果如图 3所示。
|
Download:
|
| 图 2 稀疏划分情况下不同算法的召回率对比 Fig. 2 Comparison of recall rates of different algorithms under sparse partition condition | |
|
Download:
|
| 图 3 密集划分情况下不同算法的召回率对比 Fig. 3 Comparison of recall rates of different algorithms under dense partition condition | |
对比图 2、图 3可以看出, CVAE和CDL在4组测试集上都明显优于其他2个基准算法, 在密集划分的citeulike-a测试集上, CVAE相比于ExpoMF和CTR召回率提升约14.5%和16.1%, CDL相比于ExpoMF和CTR召回率提升约10.9%和13.1%, 说明CVAE和CDL凭借VAE和SDAE强大的特征提取能力取得了优秀的推荐性能, LDA提取文本特征的能力强, 但仍不如深层非线性模型, ExpoMF虽然用EM算法对曝光隐变量进行了更细致的处理, 但由于特征向量的先验选择较差, 并且没有对曝光信息重构, 因此效果仅与CTR相当。同时可以看出, CVAE的效果优于CDL, 在密集划分的citeulike-a上, CVAE相比CDL的召回率提升约3.5%, 说明VAE的抽取特征能力强于SDAE, 这也是VAHR选择VAE而不是SDAE的原因。VAHR的效果优于CVAE和CDL, 相对于两者的召回率提升约3.8%和6.2%, 说明VAHR通过更精确的推断和对曝光信息重构, 能够更好地解决单类推荐问题。对比不同的数据集可见, 在数据集稀疏度高或规模小时, 所有模型效果均较差, 随着训练样本的增多, 所有模型召回率均有明显提升, 从稀疏划分的citeulike-a到密集划分的citeulike-t, 数据集尺寸增大约10倍, VAHR召回率提升约30.1%, 推测是由于推荐算法的训练数据量相比于参数数目来说少很多, 小数据集更易过拟合, 在测试集上表现较差。
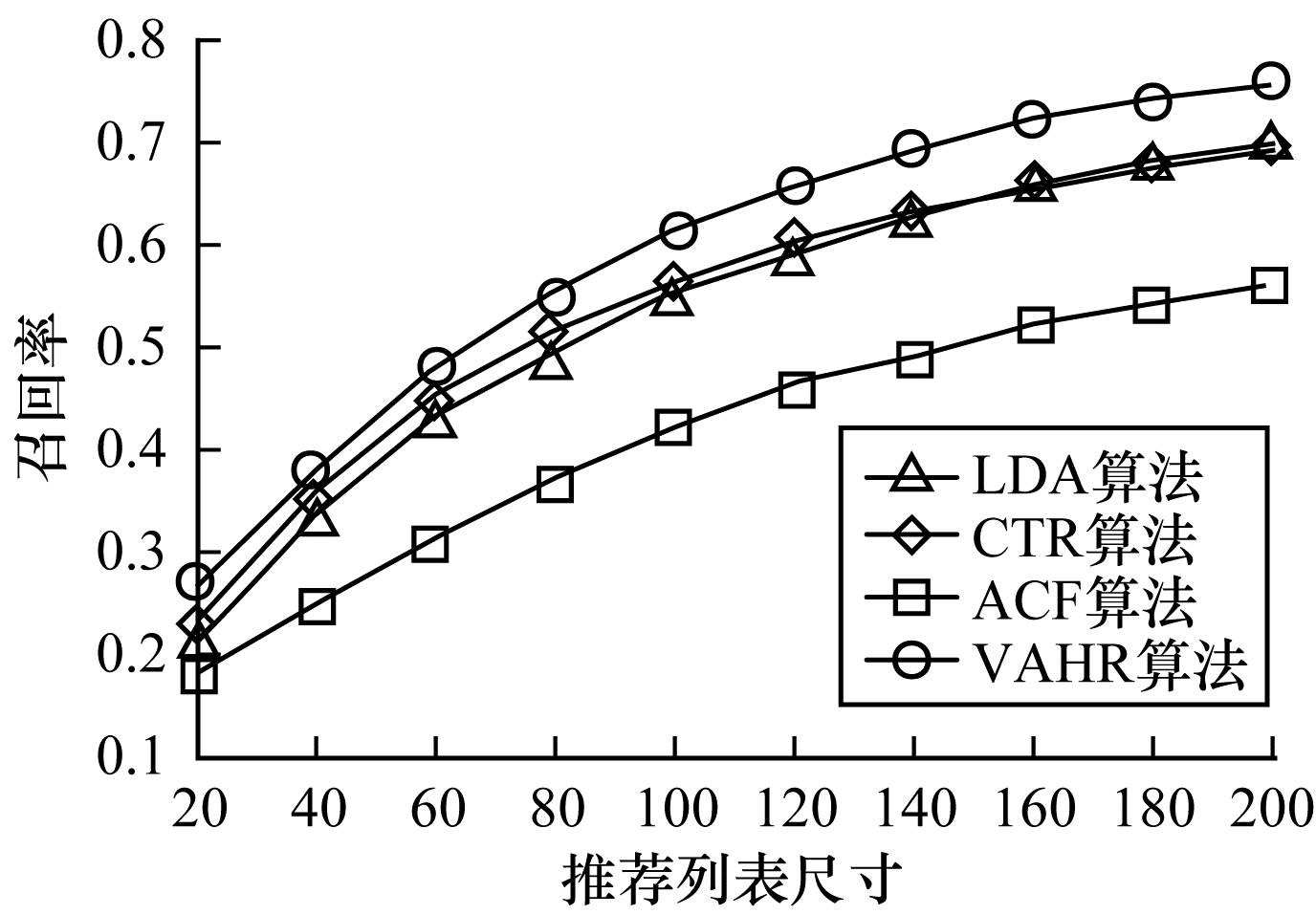
3.4.3 out-of-matrix推荐out-of-matrix推荐考虑当有一批新文章进入系统时, 应该向用户推荐新文章中的哪些文章, 即新商品的冷启动问题。这里只选择citeulike-a进行实验, 取3 396篇文章作为测试集, 其余13 584篇文章对应的用户-文章点对作为训练集。特征向量维度K=100, 推荐列表的尺寸为20, 40, …, 200, 实验结果如图 4所示。
|
Download:
|
| 图 4 K=100时citeulike-a上不同算法的召回率对比 Fig. 4 Comparison of recall rates of different algorithms on citeulike-a when K=100 | |
由图 4可见, LDA和CTR性能非常接近, 说明这两个算法受制于LDA的特征提取能力。VAHR的召回率相比CTR、LDA和ACF提升了约6.3%、6.5%和21.5%。说明VAE的特征提取能力强于SDAE和LDA, VAHR引入曝光隐变量并且让VAE直接学习商品协同隐特征, 取得了更好的新商品推荐效果。
使用以上数据集对VAHR算法选择不同的K做横向对比, K分别取25、50、75和100, 实验结果如图 5所示。
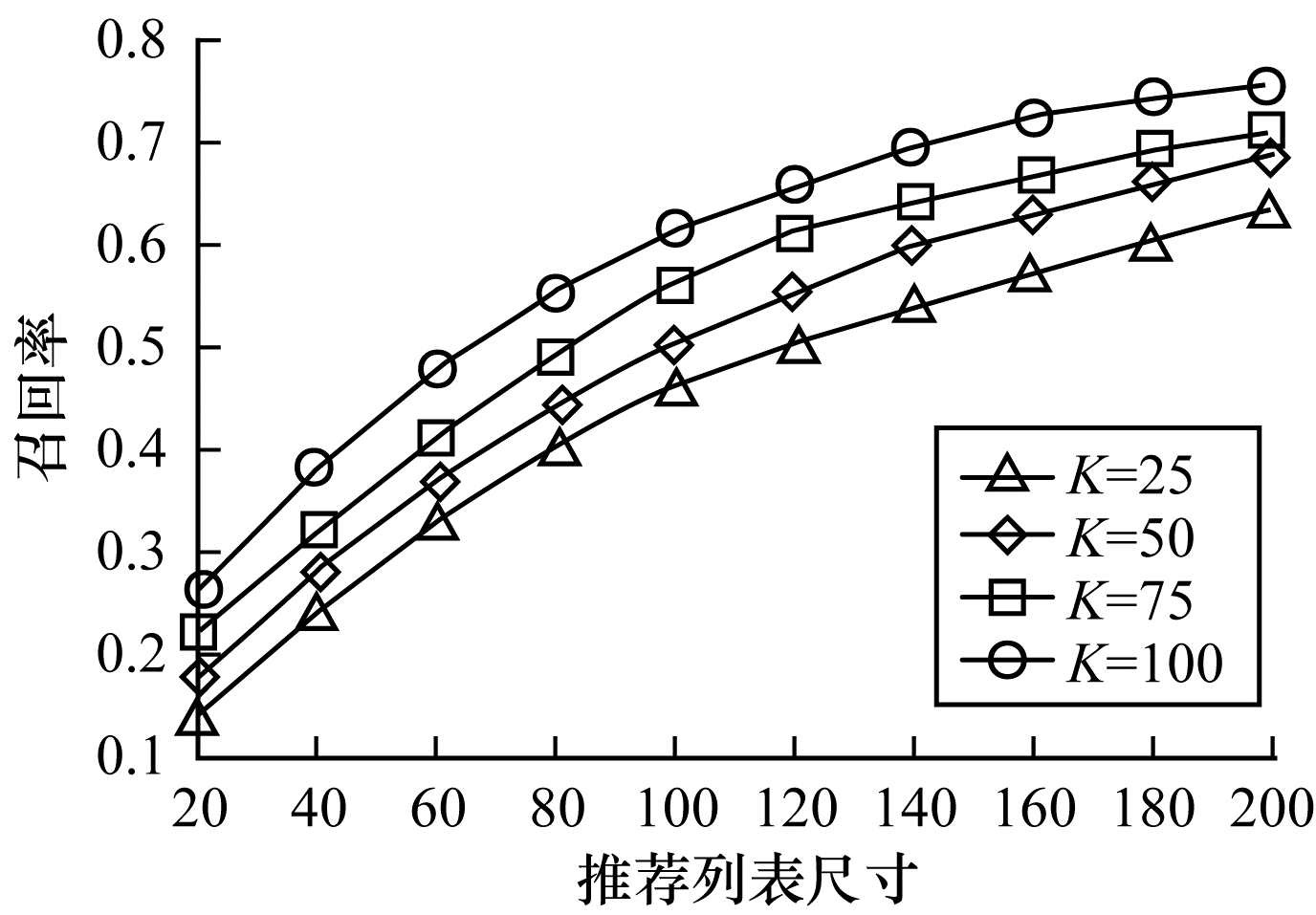
|
Download:
|
| 图 5 不同特征向量维度时citeulike-a上VAHR算法的召回率 Fig. 5 Recall rates of VAHR algorithm on citeulike-a in different feature vector dimensions | |
由图 5可见, 本文算法在K=100时相比K为25、50和75时最多取得了约14.5%、11.4%和5.5%的召回率提升。原因如下:在VAHR的前两层中都包含矩阵分解, 特征向量维度对矩阵分解的效果影响明显; 第2层的VAEi提取商品协同隐特征, 较大的K使提取出的向量表征能力更强。然而使用较大的K值会增加吉布斯采样和VAEi的训练时长, 尤其是吉布斯采样的训练时长一般以小时或天为量级, K=75与K=50的召回率相差仅3.6%, 吉布斯采样时长却相差数十小时, 因此, 在不同的推荐场景下, 应根据需求选择合适的特征维度。
4 结束语本文提出VAHR算法, 使用MCMC采样做精准参数推断, 利用变分自编码器强大的特征提取能力重构曝光信息和提取商品特征, 并在传统协同过滤算法的框架下加以改进, 以解决单类推荐问题与冷启动问题。基于citeulike-a和citeulike-t数据集的仿真实验结果表明, VAHR算法对于旧商品和新商品都能取得较好的推荐效果。下一步将在文本的预处理过程中使用LSTM或RNN等自然语言处理中经典的时序模型, 同时对吉布斯采样的并行运算加以优化, 缩短算法在大数据集中的运算时长。由于VAHR未考虑用户喜好可能会随时间推移而变化的特点, 因此还将引入时间效应, 进一步提高推荐质量。
| [1] |
YANG Bo, ZHAO Pengfei. Review of the art of recommenda-tion algorithms[J]. Journal of Shanxi University(Natural Science Edition), 2011, 34(3): 6-19. (in Chinese) 杨博, 赵鹏飞. 推荐算法综述[J]. 山西大学学报(自然科学版), 2011, 34(3): 6-19. |
| [2] |
LENG Yajun, LU Qing, LIANG Changyong. Survey of recommendation based on collaborative filtering[J]. Pattern Recognition and Artificial Intelligence, 2014, 27(8): 720-734. (in Chinese) 冷亚军, 陆青, 梁昌勇. 协同过滤推荐技术综述[J]. 模式识别与人工智能, 2014, 27(8): 720-734. |
| [3] |
SUN Yanrui, CHEN Yue. Hybrid recommendation algorithm based on Timed-HITS and collaborative filtering[J]. Journal of Northeastern University(Natural Science), 2019, 40(4): 14-19, 24. (in Chinese) 孙艳蕊, 陈月. 基于Timed-HITS与协同过滤的混合推荐算法[J]. 东北大学学报(自然科学版), 2019, 40(4): 14-19, 24. |
| [4] |
LEI Kai, LIU Shubo, LI Dan, et al. Content-based POI recommendation in real-time traffic constraint[J]. Computer Engineering, 2017, 43(10): 147-152. (in Chinese) 雷凯, 刘树波, 李丹, 等. 实时路况制约下基于内容的兴趣点推荐[J]. 计算机工程, 2017, 43(10): 147-152. |
| [5] |
KOREN Y.Factorization meets the neighborhood: a multifaceted collaborative filtering model[C]//Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2008: 426-434.
|
| [6] |
KOREN Y. Collaborative filtering with temporal dynamics[J]. Communications of the ACM, 2010, 53(4): 89-97. DOI:10.1145/1721654.1721677 |
| [7] |
CHEN Tianqi, ZHENG Zhao, LU Qiuxia, et al.Feature-based matrix factorization[EB/OL].[2019-09-11].https://arxiv.org/pdf/1109.2271.pdf.
|
| [8] |
SALAKHUTDINOV R, MNIH A.Probabilistic matrix factorization[C]//Proceedings of International Conference on Neural Information Processing Systems.New York, USA: ACM Press, 2007: 1257-1264.
|
| [9] |
SALAKHUTDINOV R, MNIH A.Bayesian probabilistic matrix factorization using Markov chain Monte Carlo[C]//Proceedings of International Conference on Machine Learning.New York, USA: ACM Press, 2008: 880-887.
|
| [10] |
LEBANON G.Local low-rank matrix approximation[C]//Proceedings of the 30th International Conference on Machine Learning.Atlanta, USA: JMLR, 2013: 82-90.
|
| [11] |
LI Mengmeng, XIA Yang, LI Xinru, et al. Dynamic hybrid recommendation algorithm based on stacked denoising autoencoder[J]. Computer Engineering, 2019, 45(8): 184-189. (in Chinese) 李梦梦, 夏阳, 李心茹, 等. 基于栈式降噪自动编码器的动态混合推荐算法[J]. 计算机工程, 2019, 45(8): 184-189. |
| [12] |
WANG C, BLEI D M.Collaborative topic modeling for recommending scientific articles[C]//Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2011: 448-456.
|
| [13] |
BLEI D, NG A, JORDAN M. Latent Dirichlet allocation[J]. Journal of Machine Learning Research, 2003, 3: 993-1022. |
| [14] |
PAN Rong, ZHOU Yunhong, CAO Bin, et al.One-class collaborative filtering[C]//Proceedings of the 8th IEEE International Conference on Data Mining.Washington D.C., USA: IEEE Press, 2008: 502-511.
|
| [15] |
HU Y, KOREN Y, VOLINSKY C.Collaborative filtering for implicit feedback datasets[C]//Proceedings of the 8th IEEE International Conference on Data Mining.Washington D.C., USA: IEEE Press, 2008: 263-272.
|
| [16] |
LIANG D, CHARLIN L, MCINERNEY J, et al.Modeling user exposure in recommendation[C]//Proceedings of the 25th International Conference on World Wide Web.[S.l.]: International World Wide Web Conferences Steering Committee, 2016: 951-961.
|
| [17] |
VINCENT P, LAROCHELLE H, LAJOIE I, et al. Stacked denoising autoencoders:learning useful representations in a deep network with a local denoising criterion[J]. Journal of Machine Learning Research, 2010, 11: 3371-3408. |
| [18] |
HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 |
| [19] |
HINTON G E. Deep belief networks[J]. Scholarpedia, 2009, 4(5): 5947. DOI:10.4249/scholarpedia.5947 |
| [20] |
KINGMA D P, WELLING M.Auto-encoding variational Bayes[EB/OL].[2019-09-11].https://arxiv.org/pdf/1312.6114.pdf.
|
| [21] |
LI X, SHE J.Collaborative variational autoencoder for recommender systems[C]//Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2017: 305-314.
|
| [22] |
WANG H, WANG N, YEUNG D Y.Collaborative deep learning for recommender systems[C]//Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2015: 1235-1244.
|
| [23] |
BOWMAN R, VILNIS L, VINYALS O, et al.Generating sentences from a continuous space[EB/OL].[2019-09-11].https://arxiv.org/pdf/1511.06349.pdf.
|
| [24] |
STRUB F, GAUDEL R, MARY J.Hybrid recommender system based on autoencoders[C]//Proceedings of the 1st Workshop on Deep Learning for Recommender Systems.New York, USA: ACM Press, 2016: 11-16.
|
 2020, Vol. 46
2020, Vol. 46
