高斯矢量多路输入信道是多个发送者分别独立地将包括时间、频率和空间的三维矢量信息传输给一个接收者, 且信道传输概率分布为高斯分布的信道, 适用于蜂窝通信的上行链路、局域网的介质接入及水声传感器网络的多址接入[1]。传统消息认证方案通常在网络层或更高层上执行, 依赖于散列函数, 使得窃听方伪造或修改的消息无法复制正确的散列标记[2]。然而, 此类消息认证方案会产生较大的计算开销, 难以适应终端资源受限的情况, 同时认证机制的安全性来自认证算法的计算复杂度。随着计算机性能的不断提升, 传统消息认证方案可能会面临新的安全威胁, 而基于物理层的消息认证方案可以快速拒绝非法消息, 降低更高层认证协议的负担, 并对阻止拒绝服务攻击特别有效[3-5]。高斯矢量多路输入信道下的消息认证方案是一种基于物理层的认证技术。本文在消息认证前先对信道状态信息进行估计, 在宽频带和多径环境中利用精确的信道估计验证物理层消息源并保护消息完整性, 而无需预先共享密钥, 从而有效降低更高层认证协议的负担[6], 并且通过使用最小均方误差(Minimum Mean Square Error, MMSE)法对高斯矢量多路输入信道进行信道估计以减少信息量损耗。
1 相关研究文献[7]提出基于物理层的消息认证方案, 将认证信息与数据并发发送, 无需额外的带宽或传输功率, 并给出了时变信道误码率的改进方法。文献[8]提出一种增强的物理层认证方案, 通过Neyman-Pearson假设检验和最小二乘自适应信道估计对突发事件中的后续帧进行认证。文献[9]基于物理层安全提出解码转发、放大转发和协同干扰3种协同方案来分配发射功率, 使发射功率约束下的可达保密率实现最大化。文献[10]针对有敌手的多路输入信道, 提出一种基于遗传算法的联合信道方案, 并使用Wyner窃听编码对信息进行保密。文献[11]研究强保密条件下多址窃听信道上的安全通信问题, 通过信道输出统计逼近方法建立强安全性的多用户信道。文献[12]提出一种基于可靠度混合重传协议的物理层安全通信技术, 与传统HARQ协议相比进一步提升了物理层通信安全。文献[13]对带有机密信息的离散无记忆多路输入信道模型进行推导, 得到不确定容量区域和保密容量区域。文献[14]推导出多路输入衰退信道下的中断容量区域, 获得每个衰落状态下的最优译码顺序和功率分配。文献[15]研究点到点的多天线安全通信方法, 使用信号与干扰加噪声比(Signal to Interference plus Noise Ratio, SINR)作为性能度量, 提出不完美信道状态下的安全通信方案。文献[16]基于高斯矢量广播信道将最优预编码结构与广义决策反馈均衡器相对应, 在发送端对高斯信道采用预编码策略获得总容量。
以上工作主要研究点到点的物理层消息认证方案, 提出多路输入信道上的安全联合信道编码和基于该信道的消息认证算法, 并计算高斯矢量广播信道的总容量及推导不同条件下多路输入信道的保密容量区域, 而高斯矢量多路输入信道下的消息认证以及该信道下的保密容量区域定界仍有待进一步研究。
2 消息认证方案 2.1 基本定义定义1 如果一个高斯矢量信道上有k(k≥2)个发送节点将消息相互独立地传输给一个接收节点, 则称其为高斯矢量多路输入信道[17]。
设高斯矢量多路输入信道模型为:
| $ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{w}}_1} $ | (1) |
其中, y为n维输出矢量, x1、x2为m维输入矢量, G1、G2为n×m维信道增益矩阵, w1~CN(0n×1, Kw1)为n维噪声矢量, Kw1为噪声矢量信号w1的协方差矩阵。
假设在如式(1)所示的信道模型中存在一个敌手Eve, 则关于Eve的窃听信道模型为:
| $ \mathit{\boldsymbol{z}} = {\mathit{\boldsymbol{G}}_3}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{G}}_4}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{w}}_2} $ | (2) |
其中, G3、G4为n×m维信道增益矩阵, w2~CN(0n×1, Kw2)为n维噪声矢量, Kw2为噪声矢量信号w2的协方差矩阵。
假设每个发送节点都可以访问多个平坦衰落信道, 并在复高斯矢量g中收集每个信道的衰落系数,同时对有M根发射天线和N根接收天线的平坦衰落信道矩阵G, 用矢量g表示为:
| $ \mathit{\boldsymbol{g}} = {[{[\mathit{\boldsymbol{G}}]_{0,0}},{[\mathit{\boldsymbol{G}}]_{1,1}}, \cdots ,{[\mathit{\boldsymbol{G}}]_{N - 1,M - 1}}]^{\rm{T}}} $ | (3) |
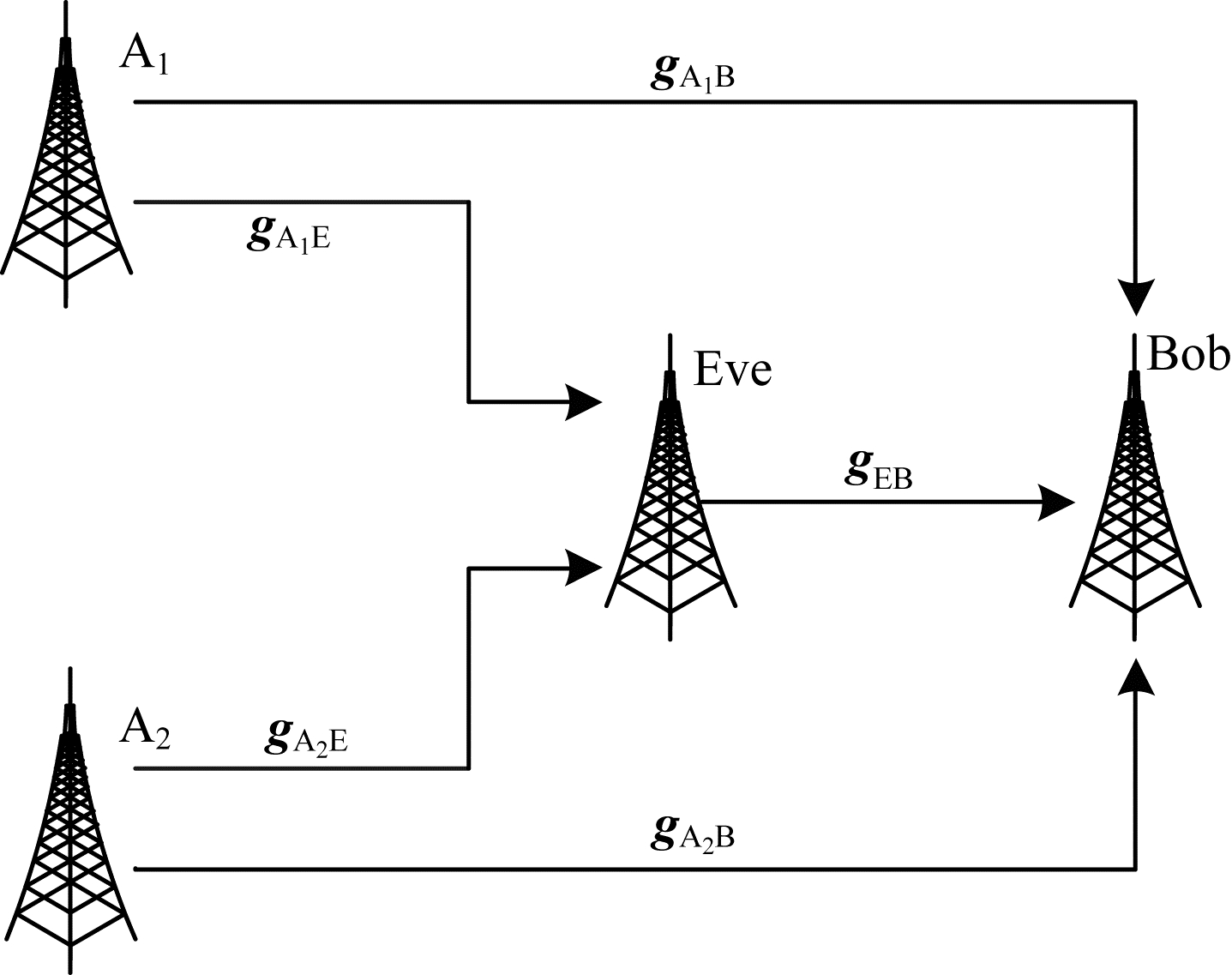
如图 1所示, A1、A2与Bob间的信道估计可以用α维的矢量分别表示为:
|
Download:
|
| 图 1 高斯矢量多路输入窃听信道模型 Fig. 1 Eavesdropping channel model of Gaussian vector multiple-input | |
| $ {{\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}} \backsim {\rm{CN}}({{\bf{0}}_{\alpha \times 1}},{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}})} $ | (4) |
| $ {{\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}} \backsim {\rm{CN}}({{\bf{0}}_{\alpha \times 1}},{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}})} $ | (5) |
同样地, A1、A2与Eve间的信道用β维的矢量分别表示为:
| $ {{\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} \backsim {\rm{CN}}({{\bf{0}}_{\beta \times 1}},{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}})} $ | (6) |
| $ {{\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}} \backsim {\rm{CN}}({{\bf{0}}_{\beta \times 1}},{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}})} $ | (7) |
Eve与Bob间的信道用γ维的矢量表示为:
| $ {\mathit{\boldsymbol{g}}_{{\rm{EB}}}} \backsim {\rm{CN}}({{\bf{0}}_{\gamma \times 1}},{\mathit{\boldsymbol{R}}_{{\rm{EB}}}}) $ | (8) |
通过对高斯矢量多路输入信道进行最小均方误差估计, 可以得到由A1、A2、Bob和Eve中任意两方构成的信道X、Y对应的协方差矩阵如式(9)所示, 例如E[gA1BgA1E]=RA1B, A1E。
| $ \mathit{\boldsymbol{E}}[{\mathit{\boldsymbol{g}}_X}{\mathit{\boldsymbol{g}}_Y}] = {\mathit{\boldsymbol{R}}_{X,Y}} $ | (9) |
定义2 信道容量C是在输入x和输出y的消息传输系统下, 概率分布函数满足∑p(y|x)=1时选择不同的概率分布p(y|x)求得I(x; y)最大值, 即[18]:
| $ C = \mathop {{\rm{max}}}\limits_{p(\mathit{\boldsymbol{x}})} \mathit{\boldsymbol{I}}(\mathit{\boldsymbol{x}};\mathit{\boldsymbol{y}}) $ | (10) |
本文提出一个高斯矢量多路输入信道下的消息认证方案, 具体分为3个阶段:
1) A1、A2分别发送给Bob一个训练序列, 假设其能被完美验证, 最初的传输可以使Bob获得关于A1、A2的参考估计信道
| $ {{{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}} = {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}{{\rm{e}}^{{\rm{j}}{\varPhi _1}}} + {\mathit{\boldsymbol{w}}_1}} $ | (11) |
| $ {{{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}} = {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}{{\rm{e}}^{{\rm{j}}{\varPhi _2}}} + {\mathit{\boldsymbol{w}}_2}} $ | (12) |
其中, w1~CN(0α×1, σ12Iα), w2~CN(0α×1, σ22Iα)。
2) A1、A2将(M1, K1)、(M2, K2)编码为x1、x2, 在t时刻将相互独立的信道输入x1、x2传输给Bob, 此时A1、A2与Bob的信道矢量分别为:
| $ {{{\mathit{\boldsymbol{\hat g}}}_1}(t) = {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}(t){{\rm{e}}^{{\rm{j}}{\varPhi _1}}} + {\mathit{\boldsymbol{w}}_3}(t)} $ | (13) |
| $ {{{\mathit{\boldsymbol{\hat g}}}_2}(t) = {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}(t){{\rm{e}}^{{\rm{j}}{\varPhi _2}}} + {\mathit{\boldsymbol{w}}_4}(t)} $ | (14) |
其中, w3(t)~CN(0α×1, σ32Iα), w4(t)~CN(0α×1, σ42Iα)。
3) Bob接收数据包y进行解码并对其来源进行认证, 该阶段可能重复多次, 通过比较当前消息执行的信道估计值
| $ \sum\limits_{t = 1}^a {\left[ {\mathit{\boldsymbol{x}}_1^{\rm{T}}(m,t){\mathit{\boldsymbol{x}}_1}(m,t) + \mathit{\boldsymbol{x}}_2^{\rm{T}}(m,t){\mathit{\boldsymbol{x}}_2}(m,t)} \right]} \le aP $ | (15) |
在第2个阶段, Eve可以估计信道并向Bob发送伪造的消息进行攻击。假设Eve已知以下信息:1)调制方案; 2)Bob采用的信道估计技术; 3)所有信道统计量, 尤其是相关矩阵; 4)gA1B、gA2B和gEB的可靠估计。
Eve处理信号的目的是修改Bob执行的信道估计。令h表示Eve预处理信道gEB后得到的等效信道, 如果在t时刻Bob接收到Eve伪造A1或A2的身份发送的消息, 则有:
| $ {{{\mathit{\boldsymbol{\hat g}}}_1}(t) = {\mathit{\boldsymbol{h}}_1}(t) + {\mathit{\boldsymbol{w}}_3}(t)} $ | (16) |
| $ {{{\mathit{\boldsymbol{\hat g}}}_2}(t) = {\mathit{\boldsymbol{h}}_2}(t) + {\mathit{\boldsymbol{w}}_4}(t)} $ | (17) |
一个安全的消息认证方案需要满足以下条件:
1) Bob经过认证拒绝接收从A1或A2发送来消息的概率为PR≤e-εi, 其中, ε>0, i是窃听信道(gA1EgA2E)的使用次数。
2) Bob经过认证接收从EVE发送来消息的概率PA, 其对于i可以忽略不计。
为验证消息的安全性, Bob使用假设检验[19]方式验证消息来源, 其中, H0表示消息来自A1和A2, H1表示消息不来自A1或A2。
本文将检验统计量设为:
| $ J = \mathop {\min }\limits_{{\varPhi _1},{\varPhi _2}} \frac{1}{{{\sigma ^2}}}\left( {\sum\limits_{n = 0}^{\alpha - 1} | {\mathit{\boldsymbol{h}}_1} - {{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}{{\rm{e}}^{{\rm{j}}{\varPhi _1}}}{|^2} + \sum\limits_{n = 0}^{\alpha - 1} | {\mathit{\boldsymbol{h}}_2} - {{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}{{\rm{e}}^{{\rm{j}}{\varPhi _2}}}{|^2}} \right) $ | (18) |
令Φ1、Φ2最小化可以减小PR的发生概率, 因此Φ1、Φ2可以取到的最小值分别为:
| $ {\varPhi _1^* = {\rm{arg}}\left( {\sum\limits_{n = 0}^{\alpha - 1} {{\mathit{\boldsymbol{h}}_1}} \mathit{\boldsymbol{\hat g}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}^*} \right)} $ | (19) |
| $ {\varPhi _2^* = {\rm{arg}}\left( {\sum\limits_{n = 0}^{\alpha - 1} {{\mathit{\boldsymbol{h}}_2}} \mathit{\boldsymbol{\hat g}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}^*} \right)} $ | (20) |
当消息来自A1、A2时, J是自由度χ为2α的中心卡方随机变量:
| $ J = \frac{1}{{{\sigma ^2}}}\left( {\sum\limits_{n = 0}^{\alpha - 1} {n_1^2} + \sum\limits_{n = 0}^{\alpha - 1} {n_2^2} } \right) \backsim \chi _{2\alpha ,0}^2 $ | (21) |
当消息来自Eve时, J是自由度χ为2α的非中心卡方随机变量:
| $ J = \frac{1}{{{\sigma ^2}}}\left( {\sum\limits_{n = 0}^{\alpha - 1} {{{(\varDelta \mathit{\boldsymbol{g}}_1^* + {n_1})}^2}} + \sum\limits_{n = 0}^{\alpha - 1} {{{(\varDelta \mathit{\boldsymbol{g}}_2^* + {n_2})}^2}} } \right) \backsim \chi _{2\alpha ,\mu }^2 $ | (22) |
其中, Δg1*、Δg2*分别为(h1-
| $ \mu = \frac{1}{{{\sigma ^2}}}\left( {\sum\limits_{n = 0}^{\alpha - 1} | {\mathit{\boldsymbol{h}}_1} - {{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}{{\rm{e}}^{{\rm{j}}\varPhi _1^*}}{|^2} + \sum\limits_{n = 0}^{\alpha - 1} | {\mathit{\boldsymbol{h}}_2} - {{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}{{\rm{e}}^{{\rm{j}}\varPhi _2^*}}{|^2}} \right) $ | (23) |
在拒绝域H0条件下, 令J < k, k是临界值, 那么可得:
| $ {{P_{\rm{R}}} = {P_{{H_0}}}(J > k) = 1 - {F_{\chi _{2\alpha ,0}^2}}(k)} $ | (24) |
| $ {{P_{\rm{A}}} = {P_{{H_0}}}(J \le k) = {F_{\chi _{2\alpha ,\mu }^2}}(k)} $ | (25) |
其中, FX是关于X的概率密度函数, 进一步可得:
| $ {P_{\rm{A}}} = {F_{\chi _{2\alpha ,{\mu _L}}^2}}(F_{\chi _{2\alpha ,0}^2}^{ - 1}(1 - {P_{\rm{R}}})) $ | (26) |
本节制定敌手对本文消息认证方案的最优攻击策略。假设Eve观察到Bob与A1、A2进行消息传输的信道估计分别为:
| $ {{{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} = {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} + {\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}} $ | (27) |
| $ {{{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}} = {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}} + {\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}}} $ | (28) |
其中, wA1E~CN(0β×1, σA1E2Iβ), wA2E~CN(0β×1, σA2E2Iβ)。
另外, 假设Eve关于Bob的信道估计为:
| $ {\mathit{\boldsymbol{\hat g}}_{{\rm{EB}}}} = {\mathit{\boldsymbol{g}}_{{\rm{EB}}}} + {\mathit{\boldsymbol{w}}_{{\rm{EB}}}} $ | (29) |
其中, wBE~CN(0γ×1, σEB2Iγ)。
通过讨论h的推导过程得出Eve的最优攻击策略, 即Eve对认证方案攻击成功概率的最大值, 并对敌手攻击成功的概率确定可达的保密边界。
3.1 敌手攻击策略设S是α复数域的子集, 并且Bob在信道估计
| $ \begin{array}{l} \mathit{\boldsymbol{\bar h}} = \mathop {{\rm{ argmax }}}\limits_{{a_1},{a_2} \in {\mathbb{C}^\alpha }} [P({{\mathit{\boldsymbol{\hat g}}}_1} \in \mathit{\boldsymbol{S}}|{\mathit{\boldsymbol{h}}_1} = {\mathit{\boldsymbol{a}}_1}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} P({{\mathit{\boldsymbol{\hat g}}}_2} \in \mathit{\boldsymbol{S}}|{\mathit{\boldsymbol{h}}_2} = {\mathit{\boldsymbol{a}}_2})] \end{array} $ | (30) |
因为Eve对gA1B、gA2B未知, 所以可以根据Eve可用的估计观测值
| $ {\mathit{\boldsymbol{R}}_1} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{A_1}B}} + \sigma _1^2{\mathit{\boldsymbol{I}}_\alpha }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}^*}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}} + \sigma _2^2{I_\alpha }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}^*}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} + \sigma _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}^2{I_\beta }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{E}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{E}}}^*}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}} + \sigma _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}^2{I_\beta }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,EB}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B,EB}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,EB}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,EB}}}^*}&{{\mathit{\boldsymbol{R}}_{{\rm{EB}}}} + \sigma _{{\rm{EB}}}^2{\mathit{\boldsymbol{I}}_\gamma }} \end{array}} \right) $ | (31) |
定义矢量Δ=[a1T, a2T,
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\bar h}} = \mathop {{\rm{ argmax }}}\limits_{{a_1},{a_2} \in {\mathbb{C} ^\alpha }} [P(\varDelta |{{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}},{{\mathit{\boldsymbol{\hat g}}}_{{\rm{EB}}}}) + P(\varDelta |{{\mathit{\boldsymbol{\hat g}}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}},{{\mathit{\boldsymbol{\hat g}}}_{{\rm{EB}}}})] = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{ argmax }}}\limits_{{a_1},{a_2} \in {\mathbb{C}^\alpha }} {\varDelta ^*}{\mathit{\boldsymbol{R}}^{ - 1}}\varDelta } \end{array} $ | (32) |
再令S=R1-1且用Sij表示S中第i行、第j列的元素, 则
| $ \mathit{\boldsymbol{\bar h}} = - {\mathit{\boldsymbol{S}}_{11}}({\mathit{\boldsymbol{S}}_{13}}{\mathit{\boldsymbol{\hat g}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} + {\mathit{\boldsymbol{S}}_{15}}{\mathit{\boldsymbol{\hat g}}_{{\rm{EB}}}}) - {\mathit{\boldsymbol{S}}_{22}}({\mathit{\boldsymbol{S}}_{24}}{\mathit{\boldsymbol{\hat g}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} + {\mathit{\boldsymbol{S}}_{25}}{\mathit{\boldsymbol{\hat g}}_{{\rm{EB}}}}) $ | (33) |
在PR取最优解的情况下分析概率PA, 令α=β=γ=N, 那么得到:
| $ {\mathit{\boldsymbol{R}}^\prime } = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + \sigma _1^2{\mathit{\boldsymbol{I}}_\alpha }}&{\bf{0}}&{{\rho _{{\rm{EB}}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}&{\bf{0}}&{{\rho _{{{\rm{A}}_1}{\rm{E}}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}\\ {\bf{0}}&{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + \sigma _2^2{\mathit{\boldsymbol{I}}_\alpha }}&{\bf{0}}&{{\rho _{{\rm{EB}}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}&{{\rho _{{{\rm{A}}_2}{\rm{E}}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}\\ {{\rho _{{\rm{EB}}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}}&{\bf{0}}&{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + \sigma _{{{\rm{A}}_1}{\rm{E}}}^2{\mathit{\boldsymbol{I}}_\beta }}&{\bf{0}}&{{\rho _{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}\\ {\bf{0}}&{{\rho _{{\rm{EB}}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}}&{\bf{0}}&{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + \sigma _{{{\rm{A}}_2}{\rm{E}}}^2{\mathit{\boldsymbol{I}}_\beta }}&{{\rho _{{{\rm{A}}_2}{\rm{B}}}}\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}\\ {{\rho _{{{\rm{A}}_1}{\rm{E}}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}}&{{\rho _{{{\rm{A}}_2}{\rm{E}}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}}&{{\rho _{{{\rm{A}}_1}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}}&{{\rho _{{{\rm{A}}_2}{\rm{B}}}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^*}}&{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} + \sigma _{{\rm{EB}}}^2{\mathit{\boldsymbol{I}}_\gamma }} \end{array}} \right) $ | (34) |
其中, Λ=diag{λ0, λ1, …, λN-1}, ρXY为与Z相连节点X、Y的空间相关系数。
此时, 对于第n个接收节点有:
| $ {\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}(n) = 1 + \frac{{\sigma _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}^2}}{{{\lambda _n}}} $ | (35) |
| $ {{\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}}(n) = 1 + \frac{{\sigma _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}^2}}{{{\lambda _n}}}} $ | (36) |
| $ {{\mathit{\boldsymbol{w}}_{{\rm{EB}}}}(n) = 1 + \frac{{\sigma _{{\rm{EB}}}^2}}{{{\lambda _n}}}} $ | (37) |
进一步代入式(30)可以得出:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\bar h}}(n) = {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}\left( {\frac{{{\rho _{{\rm{EB}}}} + {w_{{\rm{EB}}}}(n) - {\rho _{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}{\rho _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}}}{{{w_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}(n){w_{{\rm{EB}}}}(n) - \rho _{{{\rm{A}}_{\rm{1}}}{\rm{B}}}^2}}} \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{g}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}}\left( {\frac{{{\rho _{{\rm{EB}}}} + {\mathit{\boldsymbol{w}}_{{\rm{EB}}}}(n) - {\rho _{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}{\rho _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}}}}{{{\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}}(n){\mathit{\boldsymbol{w}}_{{\rm{EB}}}}(n) - \rho _{{{\rm{A}}_{\rm{2}}}{\rm{B}}}^2}}} \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{g}}_{{\rm{EB}}}}\left( {\frac{{{\rho _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} + {\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}(n) - {\rho _{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}{\rho _{{\rm{EB}}}}}}{{{\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}(n){\mathit{\boldsymbol{w}}_{{\rm{EB}}}}(n) - \rho _{{{\rm{A}}_{\rm{1}}}{\rm{B}}}^2 + }} + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\frac{{{\rho _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}} + {\mathit{\boldsymbol{w}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}}(n) - {\rho _{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}{\rho _{{\rm{EB}}}}}}{{{w_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}}(n){\mathit{\boldsymbol{w}}_{{\rm{EB}}}}(n) - \rho _{{{\rm{A}}_{\rm{2}}}{\rm{B}}}^2}}} \right)} \end{array} $ | (38) |
一个可达区域的边界函数对可以表示为:
| $ d({P_{\rm{R}}},{P_{\rm{A}}}) = {P_R}{\rm{lb}}\frac{{{P_{\rm{R}}}}}{{1 - {P_{\rm{A}}}}} + (1 - {P_{\rm{R}}}){\rm{lb}}\frac{{1 - {P_{\rm{R}}}}}{{{P_{\rm{A}}}}} $ | (39) |
| $ d({\bar P_{\rm{R}}},{\bar P_{\rm{A}}}) \le D $ | (40) |
其中, D是Bob的观测分布在任何一个假设条件下的散度。当PR→0时, 得到:
| $ {\bar P_{\rm{A}}} \ge {{\rm{e}}^{ - D}} $ | (41) |
根据消息认证方案的第2个阶段, 可以对应R1生成一个新的矩阵R2:
| $ {\mathit{\boldsymbol{R}}_2} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}} + \sigma _3^2{I_\alpha }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}^*}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}} + \sigma _4^2{\mathit{\boldsymbol{I}}_\alpha }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{1}}}{\rm{B}}}^*}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E}}}} + \sigma _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}^2{I_\beta }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{E}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,}}{{\rm{A}}_{\rm{2}}}{\rm{E}}}^*}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E}}}} + \sigma _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}^2{I_\beta }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,EB}}}}}\\ {\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,EB}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B,EB}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{E,EB}}}^*}&{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{E,EB}}}^*}&{{\mathit{\boldsymbol{R}}_{{\rm{EB}}}} + \sigma _{{\rm{EB}}}^2{\mathit{\boldsymbol{I}}_\gamma }} \end{array}} \right) $ | (42) |
根据式(31)、式(42)得到一个均值为0的协方差矩阵:
| $ \mathit{\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}} + \sigma _4^2{\mathit{\boldsymbol{I}}_\alpha }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}}\\ {{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}} + \sigma _3^2{\mathit{\boldsymbol{I}}_\alpha }}&{{\mathit{\boldsymbol{I}}_\alpha }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}} + \sigma _2^2{\mathit{\boldsymbol{I}}_\alpha }}\\ {{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}} + \sigma _1^2{\mathit{\boldsymbol{I}}_\alpha }}&{{\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B,}}{{\rm{A}}_{\rm{2}}}{\rm{B}}}}} \end{array}} \right) $ | (43) |
令T=R2-1, 用Iij表示I中第i行、第j列的元素, 由S和T可以分别得到:
| $ {\mathit{\boldsymbol{S}}_{\rm{I}}} = {\left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{S}}_{13}}}\\ {{\mathit{\boldsymbol{S}}_{14}}}\\ {{\mathit{\boldsymbol{S}}_{15}}} \end{array}} \right)^{\rm{T}}},{\mathit{\boldsymbol{S}}_{{\rm{II}}}} = {\left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{S}}_{23}}}\\ {{\mathit{\boldsymbol{S}}_{24}}}\\ {{\mathit{\boldsymbol{S}}_{25}}} \end{array}} \right)^{\rm{T}}},{\mathit{\boldsymbol{F}}_1} = \left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{S}}_{33}}}&{{\mathit{\boldsymbol{S}}_{34}}}&{{\mathit{\boldsymbol{S}}_{35}}}\\ {\mathit{\boldsymbol{S}}_{34}^*}&{{\mathit{\boldsymbol{S}}_{44}}}&{{\mathit{\boldsymbol{S}}_{45}}}\\ {\mathit{\boldsymbol{S}}_{35}^*}&{\mathit{\boldsymbol{S}}_{45}^*}&{{\mathit{\boldsymbol{S}}_{55}}} \end{array}} \right) $ | (44) |
| $ {\mathit{\boldsymbol{T}}_{\rm{I}}} = {\left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{T}}_{13}}}\\ {{\mathit{\boldsymbol{T}}_{14}}}\\ {{\mathit{\boldsymbol{T}}_{15}}} \end{array}} \right)^{\rm{T}}},{\mathit{\boldsymbol{T}}_{{\rm{II}}}} = {\left( {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{T}}_{23}}}\\ {{\mathit{\boldsymbol{T}}_{24}}}\\ {{\mathit{\boldsymbol{T}}_{25}}} \end{array}} \right)^{\rm{T}}},{\mathit{\boldsymbol{F}}_2} = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{T}}_{33}}}&{{\mathit{\boldsymbol{T}}_{34}}}&{{\mathit{\boldsymbol{T}}_{53}}}\\ {\mathit{\boldsymbol{T}}_{34}^*}&{{\mathit{\boldsymbol{T}}_{44}}}&{{\mathit{\boldsymbol{T}}_{54}}}\\ {\mathit{\boldsymbol{T}}_{35}^*}&{\mathit{\boldsymbol{T}}_{45}^*}&{{\mathit{\boldsymbol{T}}_{55}}} \end{array}} \right) $ | (45) |
至此, 可以生成一个矩阵V:
| $ \mathit{\boldsymbol{V}} = \left( {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{S}}_{\rm{I}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_1}{\kern 1pt} \mathit{\boldsymbol{S}}_{{\rm{II}}}^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_2} - {\mathit{\boldsymbol{S}}_{{\rm{II}}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_2}{\kern 1pt} \mathit{\boldsymbol{S}}_{{\rm{II}}}^{\rm{T}}}&{ - {\mathit{\boldsymbol{T}}_{{\rm{II}}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_2}{\kern 1pt} \mathit{\boldsymbol{S}}_{{\rm{II}}}^{\rm{T}}}\\ {{\mathit{\boldsymbol{S}}_{11}} - {\mathit{\boldsymbol{S}}_{\rm{I}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_1}{\kern 1pt} \mathit{\boldsymbol{S}}_{\rm{I}}^{\rm{T}}}&{{\mathit{\boldsymbol{I}}_\alpha }}&{{\mathit{\boldsymbol{T}}_2} - {\mathit{\boldsymbol{T}}_{{\rm{II}}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_2}{\kern 1pt} \mathit{\boldsymbol{T}}_{{\rm{II}}}^{\rm{T}}}\\ { - {\mathit{\boldsymbol{S}}_{\rm{I}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_1}{\kern 1pt} \mathit{\boldsymbol{T}}_{\rm{I}}^{\rm{T}}}&{{\mathit{\boldsymbol{T}}_{11}} - {\mathit{\boldsymbol{T}}_{\rm{I}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_1}{\kern 1pt} \mathit{\boldsymbol{T}}_{\rm{I}}^{\rm{T}}}&{ - {\mathit{\boldsymbol{T}}_{{\rm{II}}}}{\kern 1pt} {\mathit{\boldsymbol{F}}_1}{\kern 1pt} \mathit{\boldsymbol{T}}_{\rm{I}}^{\rm{T}}} \end{array}} \right) $ | (46) |
基于安全性检验结果, 由式(43)、式(46)最终得到散度D:
| $ D = {\rm{tr}} (\mathit{\boldsymbol{VR}}) - {\rm{lb}}|\mathit{\boldsymbol{RV}}| - 2\alpha $ | (47) |
本节将推导高斯多路输入信道在消息传输时的安全认证速率, 该速率可通过信道在功率约束P下能够达到的保密通信容量进行衡量[20]。根据消息认证方案下的信道模型, 给出有敌手的高斯矢量多路输入信道的保密容量区域。
定理1 高斯矢量多路输入信道的保密容量区域需满足以下码率对(L1, L2)组成的集合:
| $ \left\{ {\begin{array}{*{20}{l}} {{L_1} \le C({\mathit{\boldsymbol{G}}_1}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_1}}}{\kern 1pt} \mathit{\boldsymbol{G}}_1^{\rm{T}}) - C({\mathit{\boldsymbol{G}}_3}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_1}}}{\kern 1pt} \mathit{\boldsymbol{G}}_3^{\rm{T}})}\\ {{L_2} \le C({\mathit{\boldsymbol{G}}_2}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_2}}}{\kern 1pt} \mathit{\boldsymbol{G}}_2^{\rm{T}}) - C({\mathit{\boldsymbol{G}}_4}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_2}}}{\kern 1pt} \mathit{\boldsymbol{G}}_4^{\rm{T}})}\\ {{L_1} + {L_2} \le C({\mathit{\boldsymbol{G}}_1}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_1}}}{\kern 1pt} \mathit{\boldsymbol{G}}_1^{\rm{T}} + {\mathit{\boldsymbol{G}}_2}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_2}}}{\kern 1pt} \mathit{\boldsymbol{G}}_2^{\rm{T}}) - }\\ {C({\mathit{\boldsymbol{G}}_3}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_1}}}{\kern 1pt} \mathit{\boldsymbol{G}}_3^{\rm{T}} + {\mathit{\boldsymbol{G}}_4}{\kern 1pt} {\mathit{\boldsymbol{K}}_{{x_2}}}{\kern 1pt} \mathit{\boldsymbol{G}}_4^{\rm{T}})} \end{array}} \right. $ | (48) |
其中, C(Xn)=
证明
1) 逆命题证明。高斯矢量多路输入信道的安全容量可以通过具有输入代价的多路输入信道容量区域进行刻画, 对于安全信道容量L1, 有:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{L_1} \le \mathit{\boldsymbol{I}}({\mathit{\boldsymbol{x}}_1};\mathit{\boldsymbol{y}}|{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) - \mathit{\boldsymbol{I}}({\mathit{\boldsymbol{x}}_1};\mathit{\boldsymbol{z}}|{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) \mathop = \limits^{\left( a \right)} }\\ {H(\mathit{\boldsymbol{y}}|{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) - H(\mathit{\boldsymbol{y}}|{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) - H(\mathit{\boldsymbol{z}}|{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) + }\\ {H(\mathit{\boldsymbol{z}}|{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) = H({\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{w}}_1}|{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) - }\\ {H({\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{w}}_1}|{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) - }\\ {H({\mathit{\boldsymbol{G}}_3}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{G}}_4}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{G}}_2}|{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) + }\\ {H({\mathit{\boldsymbol{G}}_3}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{G}}_4}{\mathit{\boldsymbol{x}}_2} + {\mathit{\boldsymbol{G}}_2}|{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2},\mathit{\boldsymbol{Q}}) = } \end{array}\\ \begin{array}{*{20}{l}} {H({\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{w}}_1}|\mathit{\boldsymbol{Q}}) - H({\mathit{\boldsymbol{w}}_1}|\mathit{\boldsymbol{Q}}) - }\\ {H({\mathit{\boldsymbol{G}}_3}{\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{w}}_2}|\mathit{\boldsymbol{Q}}) + H({\mathit{\boldsymbol{w}}_2}|\mathit{\boldsymbol{Q}}) \mathop \le \limits^{\left( b \right)} }\\ {\frac{1}{2}{\rm{lb}}|2{\rm{ \mathsf{ π} e}}({\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_1^{\rm{T}} + {\mathit{\boldsymbol{I}}_n})| - } \end{array}\\ \begin{array}{*{20}{l}} {\frac{1}{2}{\rm{lb}}|2{\rm{ \mathsf{ π} e}}{\mathit{\boldsymbol{I}}_n}| - \frac{1}{2}{\rm{lb}}|2{\rm{ \mathsf{ π} e}}({\mathit{\boldsymbol{G}}_3}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_3^{\rm{T}}) + {\mathit{\boldsymbol{I}}_n}| + }\\ {\frac{1}{2}{\rm{lb}}|2{\rm{ \mathsf{ π} e}}{I_n}| = \frac{1}{2}{\rm{lb}}|{\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_1^{\rm{T}} + {\mathit{\boldsymbol{I}}_n}| - }\\ {\frac{1}{2}{\rm{lb}}|{\mathit{\boldsymbol{G}}_3}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_3^{\rm{T}} + {\mathit{\boldsymbol{I}}_n}| = }\\ {C({\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_1^{\rm{T}}) - C({\mathit{\boldsymbol{G}}_3}\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_3^{\rm{T}})} \end{array} \end{array} $ | (49) |
其中, H为信息熵, Q是一个与信道参数无关的分时随机变量, Q→(x1, x2)→y构成一个马尔科夫链, (a)表示根据互信息量I的定义, (b)表示由最大微分熵引理[17]得出。对于L2和(L1+L2)的证明同理。
2) 可达性证明。令x1+x2~N(0, P), 得到:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{I}}({\mathit{\boldsymbol{x}}_1};\mathit{\boldsymbol{y}}|{\mathit{\boldsymbol{x}}_2}) = C({\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_1^{\rm{T}})}\\ {\mathit{\boldsymbol{I}}({\mathit{\boldsymbol{x}}_2};\mathit{\boldsymbol{y}}|{\mathit{\boldsymbol{x}}_1}) = C({\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{K}}_{{x_2}}}\mathit{\boldsymbol{G}}_2^{\rm{T}})}\\ {\mathit{\boldsymbol{I}}({\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2};\mathit{\boldsymbol{y}}) = C({\mathit{\boldsymbol{G}}_1}{\mathit{\boldsymbol{K}}_{{x_1}}}\mathit{\boldsymbol{G}}_1^{\rm{T}} + {\mathit{\boldsymbol{G}}_2}{\mathit{\boldsymbol{K}}_{{x_2}}}\mathit{\boldsymbol{G}}_2^{\rm{T}})} \end{array}} \right. $ | (50) |
对j∈N*, 令[x1]j, [x2]j∈{-jφ, -(j-1)φ, …, -φ, 0, φ, …, jφ}为x1、x2的离散采样, 其中φ=1/
| $ \left\{ {\begin{array}{*{20}{l}} {{L_1} \le \mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_1}]}_j};{{[{\mathit{\boldsymbol{y}}_j}]}_k}|{{[{\mathit{\boldsymbol{x}}_2}]}_j}) - \mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_1}]}_j};{{[{\mathit{\boldsymbol{z}}_j}]}_k}|{{[{\mathit{\boldsymbol{x}}_2}]}_j})}\\ {{L_2} \le \mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_2}]}_j};{{[{\mathit{\boldsymbol{y}}_j}]}_k}|{{[{\mathit{\boldsymbol{x}}_1}]}_j}) - \mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_2}]}_j};{{[{\mathit{\boldsymbol{z}}_j}]}_k}|{{[{\mathit{\boldsymbol{x}}_1}]}_j})}\\ {{L_1} + {L_2} \le \mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_1}]}_j},{{[{\mathit{\boldsymbol{x}}_2}]}_j};{{[{\mathit{\boldsymbol{y}}_j}]}_k}) - \mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_1}]}_j},{{[{\mathit{\boldsymbol{x}}_2}]}_j};{{[{\mathit{\boldsymbol{z}}_j}]}_k})} \end{array}} \right. $ | (51) |
由数据处理不等式可得:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_1}]}_j};{{[{\mathit{\boldsymbol{y}}_j}]}_k}|{{[{\mathit{\boldsymbol{x}}_2}]}_j}) \le \mathit{\boldsymbol{I}}({{[{\mathit{\boldsymbol{x}}_1}]}_j};{\mathit{\boldsymbol{y}}_j}|{{[{\mathit{\boldsymbol{x}}_2}]}_j}) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} H({\mathit{\boldsymbol{y}}_j}|{{[{\mathit{\boldsymbol{x}}_2}]}_j}) - H({\mathit{\boldsymbol{w}}_1})} \end{array} $ | (52) |
因为对所有j有Var(yj|[x2]j)≤G1Kx1G1T+1, 即H(yj|[x2]j)≤H(y|x2), 所以:
| $ \mathit{\boldsymbol{I}}({[{\mathit{\boldsymbol{x}}_1}]_j};{[{\mathit{\boldsymbol{y}}_j}]_k}|{[{\mathit{\boldsymbol{x}}_2}]_j}) \le \mathit{\boldsymbol{I}}({\mathit{\boldsymbol{x}}_1};\mathit{\boldsymbol{y}}|{\mathit{\boldsymbol{x}}_2}) $ | (53) |
最终将结果代入式(50)和式(51), 证毕。
5 实验结果与分析实验环境配置为IntelⓇCoreTMi5-4210U CPU@ 1.70 GHz、双核、4 GB RAM、Windows 10操作系统。编程环境为Matlab R2014a。通过设置不同的信道条件来观察Eve攻击成功的概率均值 PA的变化情况, 分析并研究消息认证方案的安全性能。
5.1 度量标准根据消息认证方案可以得出第1个阶段信道的信噪比S1和S2为:
| $ {S_1} = \frac{1}{{\alpha \sigma _1^2}} {\rm{tr}} ({\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}),{S_2} = \frac{1}{{\alpha \sigma _2^2}} {\rm{tr}} ({\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}) $ | (54) |
同理, 第2个阶段信道的信噪比S3和S4为:
| $ {S_3} = \frac{1}{{\alpha \sigma _3^2}} tr ({\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{1}}}{\rm{B}}}}),{S_4} = \frac{1}{{\alpha \sigma _4^2}} {\rm{tr}} ({\mathit{\boldsymbol{R}}_{{{\rm{A}}_{\rm{2}}}{\rm{B}}}}) $ | (55) |
令η=(1+S1-1)(1+S3-1)+(1+S2-1)(1+S4-1), 那么式(47)可以改写为:
| $ \begin{array}{*{20}{l}} {D = 2N({\rho _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}}{\rho _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}} - \rho _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}^2\rho _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}^2)/[\eta - \rho _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}^2\rho _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}^2] - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} N{\rm{lb}}[(\eta - 1)/(\eta - \rho _{{{\rm{A}}_{\rm{1}}}{\rm{E}}}^2\rho _{{{\rm{A}}_{\rm{2}}}{\rm{E}}}^2)]} \end{array} $ | (56) |
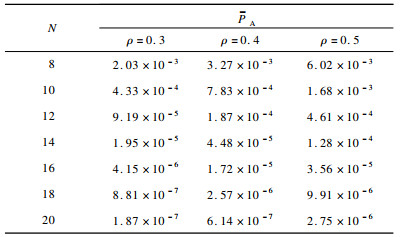
本节通过实验观察高斯矢量多路输入信道模型在不同条件下的安全性能。表 1刻画了Eve攻击成功的概率均值PA在不同信道条件下的变化关系。假设S1=S2=15 dB、S3=S4=20 dB, 并令ρA1E=ρA2E=ρ, 其中显示了ρ分别为0.3、0.4和0.5时PA随N的变化情况。由实验结果可知, 随着节点数N的增大, Eve攻击成功的概率均值PA呈指数级降低, 这是由于节点间存在波束成形使得Eve收到的信号减弱。当N=20且A1、A2与Eve的相关系数都小于0.3时, 敌手攻击成功的概率均值小于1.87×10-7。
|
下载CSV 表 1 信道变量N、ρ与Eve攻击成功概率均值PA的关系 Table 1 Relationship between channel variables N, ρ and the average probability of successful Eve attack PA |
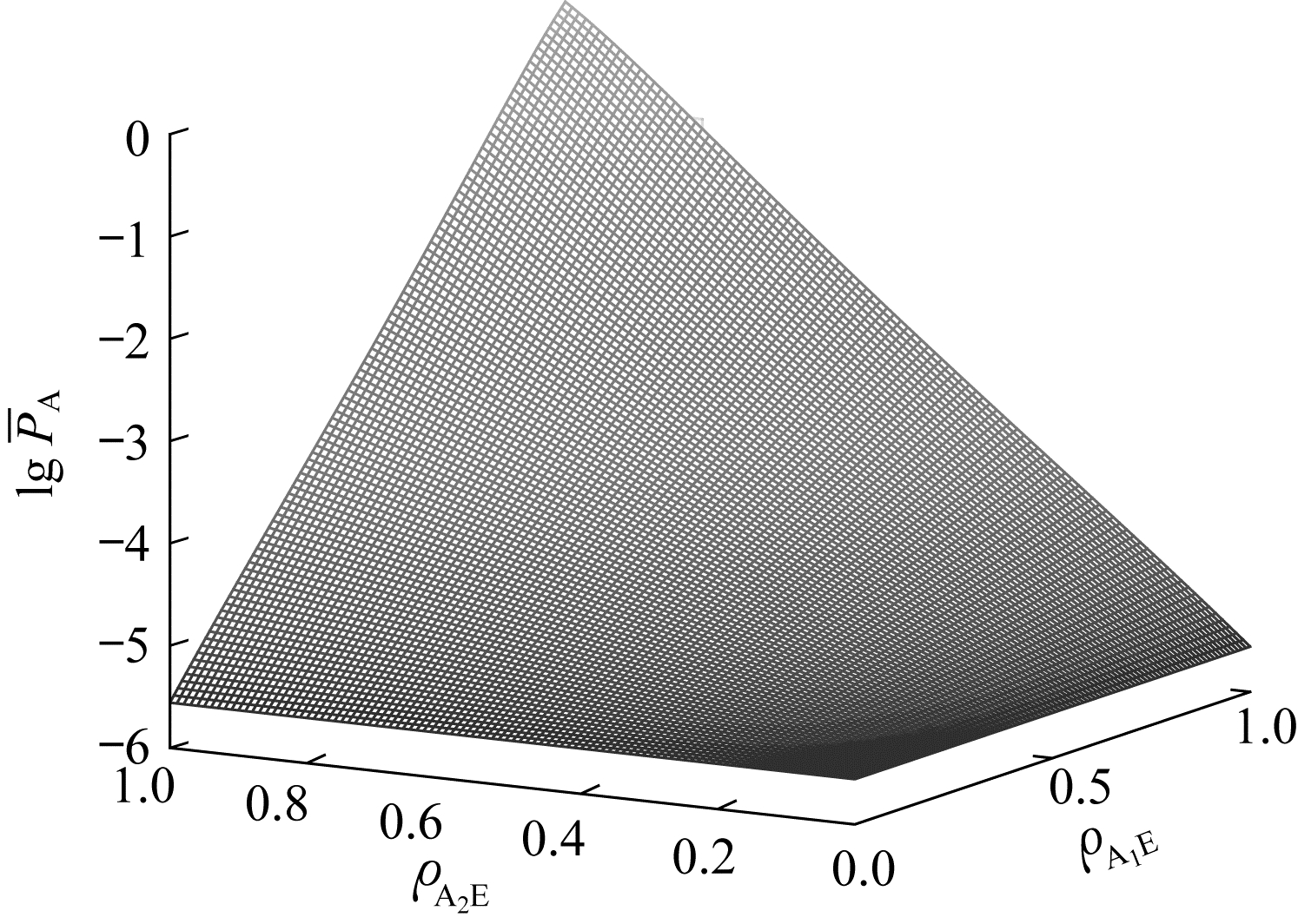
图 2给出Eve与A1、A2关联信道的空间相关系数ρA1E、ρA2E与Eve攻击成功的概率均值PA之间的关系。初始假设条件与表 1相同, 并将节点数N固定为20。由实验结果可知, 随着发送者与敌手关联空间相关系数的减小, Eve攻击成功的概率均值PAA呈指数级下降, 即使当Eve估计出一侧的信道信息而对另一侧了解较少时, PA仍处于一个较低的范围区间。
|
Download:
|
| 图 2 空间相关系数ρA1E、ρA2E与Eve攻击成功概率均值PA的关系模型 Fig. 2 The relational model among the spatial correlation coefficients ρA1E, ρA2E and the average probability of successful Eve attack PA | |
图 3给出了第1个阶段信道的信噪比S1、S2与Eve攻击成功的概率均值PA的关系, 假设S1=S2=15 dB, ρA1E=ρA2E=0.5。实验结果表明, 在第1个阶段发送训练序列时的信噪比越大, 安全性越强。当S1和S2为(0 dB, 5 dB)时, 则安全性迅速提升; 当S1和S2大于15 dB时, 则安全性提升效果趋于减缓。

|
Download:
|
| 图 3 信噪比S1、S2与Eve攻击成功概率均值PA的关系模型 Fig. 3 The relational model among the signal to noise ratio S1, S2 and the average probability of successful Eve attack PA | |
本文利用最小均方误差法进行信道估计, 提出一种高斯矢量多路输入信道下的消息认证方案, 运用假设检验方法对消息认证方案进行安全性检验, 制定敌手的最优攻击策略, 并对敌手攻击成功的概率进行定界, 同时在发送功率受约束的情况下, 推导出消息认证方案的保密容量区域。通过实验测试与分析该方案在不同信道条件下敌手攻击成功的概率, 从而验证其安全性和可行性, 为多路输入信道下物理层消息认证的安全性分析提供了参考。后续将针对高斯矢量广播信道等其他信道模型下的物理层消息认证方案做进一步研究。
| [1] |
JEREMY P V, PHILIP S. Expectation-maximization Gaussian-mixture approximate message passing[J]. IEEE Transactions on Signal Processing, 2013, 61(19): 4658-4672. DOI:10.1109/TSP.2013.2272287 |
| [2] |
XIAO L, GREENSTEIN L, MANDAYAM N, et al.MIMO-assisted channel-based authentication in wireless networks[C]//Proceedings of the 42nd Annual Conference on Information Sciences and Systems.Washington D.C., USA: IEEE Press, 2008: 642-646.
|
| [3] |
VISURI S, BOLCSKEI H.MIMO-OFDM multiple access with variable amount of collision[C]//Proceedings of 2004 IEEE International Conference on Communications.Washington D.C., USA: IEEE Press, 2004: 286-291.
|
| [4] |
YANG Xiaodong, LI Yanan, ZHOU Qixu, et al. ID-based sever-aided verification proxy re-signature scheme[J]. Computer Engineering, 2017, 43(4): 166-170, 176. (in Chinese) 杨小东, 李亚楠, 周其旭, 等. 基于身份的服务器辅助验证代理重签名方案[J]. 计算机工程, 2017, 43(4): 166-170, 176. |
| [5] |
YU Binbin, HU Liang, CHI Ling. Digital signature scheme against internal and external attack for wireless sensor networks[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(5): 1676-1681. (in Chinese) 于斌斌, 胡亮, 迟令. 可抵抗内外部攻击的无线传感器网络数字签名方案[J]. 吉林大学学报(工学版), 2019, 49(5): 1676-1681. |
| [6] |
PAOLO B, NICOLA L, STEFANO T. Physical layer authentication over MIMO fading wiretap channels[J]. IEEE Transactions on Wireless Communications, 2012, 11(7): 2564-2573. DOI:10.1109/TWC.2012.051512.111481 |
| [7] |
YU P L, BARAS J S, SADLER B M. Physical-layer authentication[J]. IEEE Transactions on Information Forensics and Security, 2008, 3(1): 38-51. DOI:10.1109/TIFS.2007.916273 |
| [8] |
XIAO L, GREENSTEIN L, MANDAYAM N, et al.A physical-layer technique to enhance authentication for mobile terminals[C]//Proceedings of 2008 IEEE Inter-national Conference on Communications.Washington D.C., USA: IEEE Press, 2008: 1520-1524.
|
| [9] |
LUN D, ZHU H, PETROPULU A P, et al. Improving wireless physical layer security via cooperating relays[J]. IEEE Transactions on Signal Processing, 2010, 58(3): 1875-1888. DOI:10.1109/TSP.2009.2038412 |
| [10] |
SADAF S, MOHAMMAD R A.Joint source-channel coding for multiple-access wiretap channels[C]//Proceedings of IEEE International Symposium on Information Theory.Washington D.C., USA: IEEE Press, 2013: 369-373.
|
| [11] |
YASSAEE M H, AREF M R.Multiple access wiretap channels with strong secrecy[C]//Proceedings of 2010 IEEE Information Theory Workshop.Washington D.C., USA: IEEE Press, 2010: 1-5.
|
| [12] |
ZOU Qinyu, ZHANG Bangning, GUO Daoxing, et al. Physical layer safety communication technology based on reliability mixed restansmission protocol[J]. Computer Engineering, 2018, 44(1): 182-186, 192. (in Chinese) 邹芹宇, 张邦宁, 郭道省, 等. 基于可靠度混合重传协议的物理层安全通信技术[J]. 计算机工程, 2018, 44(1): 182-186, 192. |
| [13] |
LIANG Y B, POOR H V. Multiple-access channels with confidential messages[J]. IEEE Transactions on Information Theory, 2008, 54(3): 976-1002. DOI:10.1109/TIT.2007.915978 |
| [14] |
LI L, JINDAL N, GOLDSMITH A. Outage capacities and optimal power allocation for fading multiple-access channels[J]. IEEE Transactions onInformation Theory, 2005, 51(4): 1326-1347. DOI:10.1109/TIT.2005.844065 |
| [15] |
MUKHERJEE A, SWINDLEHURST A L. Robust beamforming for security in MIMO wiretap channels with imperfect CSI[J]. IEEE Transactions on Signal Processing, 2011, 59(1): 351-361. DOI:10.1109/TSP.2010.2078810 |
| [16] |
YU W, CIOFFI J M. Sum capacity of Gaussian vector broadcast channels[J]. IEEE Transactions on Information Theory, 2004, 50(9): 1875-1892. DOI:10.1109/TIT.2004.833336 |
| [17] |
ABBAS E G, YOUNG-HAN K. Network information theory[M]. London, UK: Cambridge University Press, 2011: 230-234.
|
| [18] |
MARTINIAN E, WORNELL G W, CHEN B. Authentication with distortion criteria[J]. IEEE Transactions on Information Theory, 2005, 51(7): 2523-2542. DOI:10.1109/TIT.2005.850123 |
| [19] |
MAURER U M. Authentication theory and hypothesis testing[J]. IEEE Transactions on Information Theory, 2000, 46(4): 1350-1356. DOI:10.1109/18.850674 |
| [20] |
COVER T, MCELIECE R, POSNER E. Asynchronous multiple-access channel capacity[J]. IEEE Transactions on Information Theory, 1981, 27(4): 409-413. DOI:10.1109/TIT.1981.1056382 |
 2020, Vol. 46
2020, Vol. 46
