b. 空军工程大学 防空反导学院, 西安 710051
b. College of Air and Missile Defense, Air Force Engineering University, Xi'an 710051, China
网络作为信息传播的主要载体已广泛应用于生产和生活各方面, 但由于其安全机制不完善, 在给人们带来便利的同时也存在安全隐患。因此, 如何准确评价网络状态并提供有效的安全防护指导成为研究人员关注的热点, 网络安全态势预测(Network Security Situation Prediction, NSSP)由此应运而生。网络安全态势预测是基于所识别的攻击活动及网络态势, 对已出现与将出现的网络攻击行为所产生的危害和潜在威胁进行评估[1]。
随着网络安全态势预测算法的不断进步, 网络安全态势预测已由根据研究人员的定性经验知识或网络数据进行预测发展为基于半定量数据(包含定性经验知识与网络中采集到的定量数据)进行预测[2], 其中置信规则库(Belief Rule Base, BRB)是基于半定量数据的典型模型之一。根据定性经验知识建立初始的置信规则库, 采用负反馈方法进行参数优化, 最终可得到较准确的基于置信规则库的网络安全态势预测模型。文献[3]提出利用MATLAB工具箱中Fmincon函数优化置信规则库参数的方法, 但在置信规则库模型规模较大时优化速度较慢且不具备可移植性。针对该问题, 文献[4]提出基于遗传算法的模型参数优化方法来提高优化算法的可移植性; 文献[5]提出基于改进粒子群算法的模型参数优化算法, 在一定程度上提高了模型优化的速度和准确性; 文献[6]提出基于冗余基因策略的模型参数优化方法, 可自动生成具有不同数量规则的BRB最优解。上述方法均为模型整体优化方法, 在一定程度上可提高优化效率, 但在训练数据分布不均时模型预测准确性较低。对置信规则库推理过程分析可知, 置信规则库中规则的作用范围有限, 且模型预测精度较低的区域通常位于未充分优化规则处。
针对上述问题, 本文提出一种采用分级优化置信规则库(Hierarchically Optimized Belief Rule Base, HOBRB)的预测方法。设定临界值将规则划分为可充分优化、可部分优化、不可优化3个等级, 保留专家赋值的部分参数减少规则中待优化参数量, 以避免在训练数据较少时产生过拟合现象。
1 置信规则库 1.1 置信规则库的表示置信规则由YANG等人[7]基于传统IF-THEN规则提出, 其引入分布式置信框架和权重参数, 并以分布式置信度形式表示输出结果。一系列置信规则构成置信规则库, 其中第k条置信规则表示为:
| $ \begin{array}{l} {R_k}:{\rm{if}}({x_1}{\kern 1pt} {\kern 1pt} {\rm{is}}{\kern 1pt} {\kern 1pt} A_1^k) \wedge ({x_2}{\kern 1pt} {\kern 1pt} {\rm{is}}{\kern 1pt} {\kern 1pt} A_2^k) \wedge \cdots \wedge ({x_M}{\kern 1pt} {\kern 1pt} {\rm{is}}{\kern 1pt} {\kern 1pt} A_M^k)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Then}}\{ ({D_1},{\beta _{1,k}}),({D_2},{\beta _{2,k}}), \cdots ,({D_N},{\beta _{N,k}})\} \end{array} $ | (1) |
其中:xi为输入参数的第i个前提属性, i=1, 2, …, M, M为前提属性个数; Aik为第k条规则中第i个输入的参考值, k=1, 2, …, L, i=1, 2, …, M, L为置信规则库中置信规则个数; Dj为结果属性的第j个评价等级, j=1, 2, …, N, N为评价等级个数; βj, k为第k条规则中第j个评价等级的置信度, j=1, 2, …, N, k=1, 2, …, L, 如果
在置信规则库推理过程中, 使用证据推理(Evidential Reasoning, ER)算法[8-9]合成激活规则, 并由此得到BRB系统的最终输出。
1.2.1 激活权重计算当输入信息x=(x1, x2, …, xM)时, xi相对参考值Aik的匹配度计算公式为:
| $ a_i^k = \left\{ {\begin{array}{*{20}{l}} {\frac{{A_i^{l + 1} - {x_i}}}{{A_i^{l + 1} - A_i^l}},k = l{\rm{ 且 }}A_i^l \le {x_i} \le A_i^{l + 1}}\\ {1 - a_i^l,k = l + 1}\\ {0,k = 1,2, \cdots ,N{\rm{ 且 }}k \ne l,l + 1} \end{array}} \right. $ | (2) |
其中, aik(i=1, 2, …, M)为系统输入x的第i个前提属性值相对于第k条规则中第i个属性参考值的匹配度, Ail和Ail+1分别为第i个前提属性中相邻两个参考值。可将xi转换为等级分布评价形式S(xi)={(Aij, aij), j=1, 2, …, Ji}, Ji为第i个前提属性的参考值个数, 结合属性权重δi与规则权重θk计算第k条规则的激活权重, 计算公式为:
| $ {w_k} = \frac{{{\theta _k}\prod\limits_{i = 1}^M {{{(\alpha _i^k)}^{{{\bar \delta }_i}}}} }}{{\sum\limits_{l = 1}^L {{\theta _l}} \prod\limits_{i = 1}^M {{{(\alpha _i^l)}^{{{\bar \delta }_i}}}} }} $ | (3) |
其中,
利用ER解析算法对L条规则进行融合, 计算公式为:
| $ \begin{array}{l} {{\hat \beta }_i} = \\ \frac{{\mu \times \left[ {\prod\limits_{k = 1}^N {\left( {{w_k}{\beta _{j,k}} + 1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j,k}}} } \right)} - \prod\limits_{k = 1}^N {\left( {1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j,k}}} } \right)} } \right]}}{{1 - \mu \times \left[ {\prod\limits_{k = 1}^L {(1 - {w_k})} } \right]}} \end{array} $ | (4) |
| $ {\hat \beta _D} = 1 - \sum\limits_{j = 1}^N {{\beta _j}} $ | (5) |
| $ \begin{array}{*{20}{l}} {\mu = \left[ {\sum\limits_{j = 1}^N {\prod\limits_{k = 1}^N {\left( {{w_k}{\beta _{j,k}} + 1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j,k}}} } \right)} } - } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left. {(N - 1)\prod\limits_{k = 1}^N {\left( {1 - {w_k}\sum\limits_{j = 1}^N {{\beta _{j,k}}} } \right)} } \right]}^{ - 1}}} \end{array} $ | (6) |
其中,
| $ S(x) = \{ ({D_j},{\hat \beta _j}),j = 1,2, \cdots ,N\} $ | (7) |
通过效用值将结果由置信度转换为数值。设在评价等级Dj上效用值为μ(Dj)(j=1, 2, …, N), 则系统输出S(x)的期望效用值表示为:
| $ \mu (S(x)) = \sum\limits_{j = 1}^N \mu ({D_j}){\hat \beta _j} $ | (8) |
其中,
当评价不完整或不精确时, 最大效用、最小效用和平均效用分别定义[11]如下:
| $ {{\mu _{\max }}(S(x)) = \sum\limits_{i = 1}^{N - 1} \mu ({D_i}){{\hat \beta }_i} + \mu ({D_N})({{\hat \beta }_N} + {{\hat \beta }_D})} $ | (9) |
| $ {{\mu _{\min }}(S(x)) = \mu ({D_1})({{\hat \beta }_1} + {{\hat \beta }_D}) + \sum\limits_{i = 2}^N \mu ({D_i}){{\hat \beta }_i}} $ | (10) |
| $ {{\mu _{{\rm{avg}}}}(S(x)) = \frac{{{\mu _{\max }}(S(x)) + {\mu _{\min }}(S(x))}}{2}} $ | (11) |
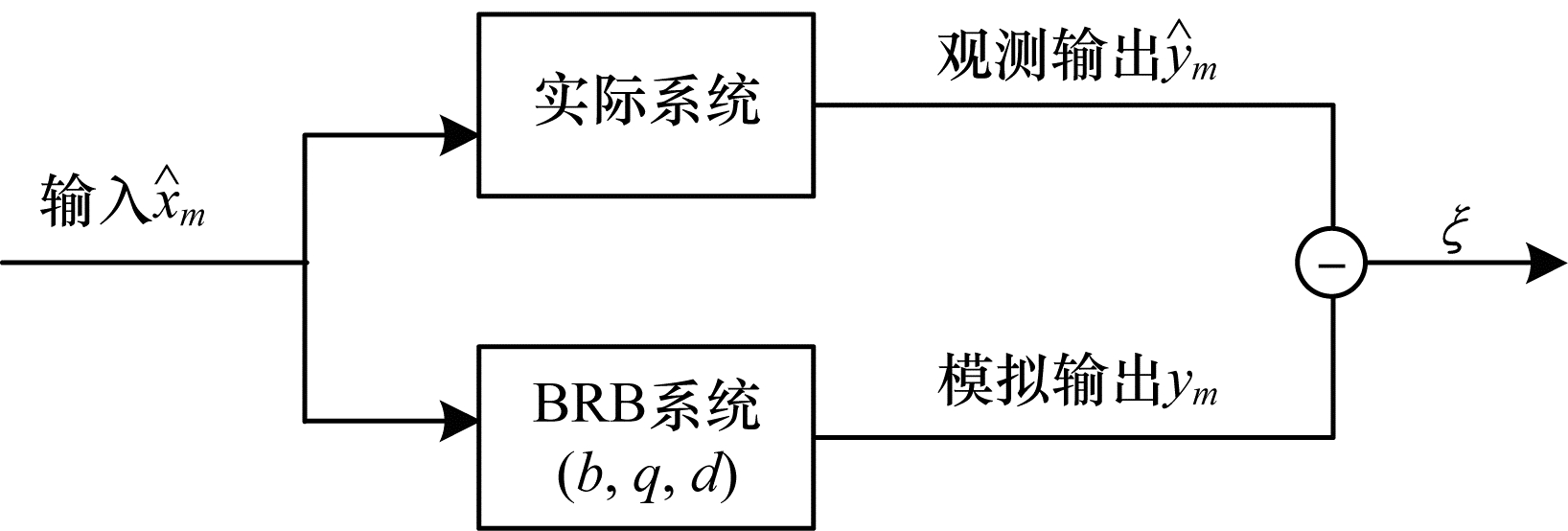
由于研究人员对模型作用对象的认识可能存在误差, 造成初始置信规则库精度不高, 因此文献[3]提出一种通过定量数据对置信规则库参数进行优化的方法, 将参数学习转化为求解最优化模型, 置信规则库优化模型如图 1所示。
|
Download:
|
| 图 1 置信规则库优化模型 Fig. 1 BRB optimization model | |
利用MATLAB工具箱中的Fmincon函数求解该模型, 计算公式为:
| $ \begin{array}{*{20}{l}} {\min \{ \xi (\mathit{\boldsymbol{P}})\} }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}0 \le {\theta _k} \le 1,k = 1,2, \cdots ,L}\\ {\qquad \begin{array}{*{20}{l}} {0 \le {\delta _{i,k}} \le 1,i = 1,2, \cdots ,M,k = 1,2, \cdots ,L}\\ {0 \le {\beta _{i,k}} \le 1,j = 1,2, \cdots ,N,k = 1,2, \cdots ,L}\\ {\sum\limits_{j = 1}^N {{\beta _{i,k}}} = 1} \end{array}} \end{array} $ | (12) |
其中, P=(θ1, θ2, …, θL, β1, 1, β2, 2, …, βN, L, δ1, 1, δ2, 2, …, δL, M)为置信规则库优化模型的参数向量, ubi和lbi分别代表第i个前提属性参考值的上、下边界值。目标函数可用平均绝对误差(Mean Absolute Error, MAE)表示, 表达式为:
| $ \xi (P) = \frac{1}{M}\sum\limits_{m = 1}^M | {y_m} - {\hat y_m}| $ | (13) |
传统BRB模型优化方法均假设规则的作用范围为全局, 优化目标函数设为模型相对全部训练样本的平均绝对误差, 通过导入训练数据并利用负反馈方法进行全局优化。但由式(2)可知, 输入数据的每个前提属性值可用相邻一组或两组参考值的置信度形式表示, 因此模型推理中每组输入只激活有限条规则, 且每条规则的作用范围有限。
置信规则库模型推理的本质是在模型作用域中插入若干参考点, 利用由参考点确定的平面将整个作用域划分为多个子域, 位于子域中待求解点处的推理由多个子域边界参考点共同作用完成。模型作用域的维数为前提属性个数M, 作用域中每个参考点对应规则库中的一条规则, 其中第k个参考点的坐标为(Ak1, Ak2, …, AkM)、模型输出为μk(D), 该参考点对周围区域的影响参数为wk, 各维参数的相对影响力为δi, k(i=1, 2, …, M), 参考点总数
以模型作用域中参考点为顶点的子域集合即该参考点对应规则的作用范围, 称为规则作用域。在模型优化过程中, 由于某些规则作用域中训练数据较少造成规则训练不充分, 导致出现过拟合现象, 因此应针对不同类型的规则采用不同优化训练方法。本文提出的HOBRB模型建立步骤如下:
1) 建立模型作用空间, 划分规则作用域。将置信规则库每一个输入属性作为一维, 将模型作用范围表示为M维空间中的立方体, 以规则输入属性参考值为坐标将各条规则表示为空间中的参考点。建立经过参考点并垂直于坐标轴的平面, 将模型作用域划分为出
2) 将训练数据分配到对应规则作用区域, 以训练数据的前提属性值组合(x1, x2, …, xM)为坐标, 将训练数据表示为模型作用域中的坐标点, 根据坐标点的空间位置确定训练数据所属的规则作用域。将位于训练子域边界的训练数据按照右侧分配的原则分配到数值增大的规则作用域中。
3) 为规则划分等级。规则中包括规则权重、评价等级置信度、前提属性权重等共C1个待优化的参数, 其中C1=1+M+N。当规则作用域中训练数据的数量大于C1时, 由求解方程组过程中未知量与已知条件的关系可知规则参数存在唯一解, 其可由求解最小值的方法求出, 位于此等级的规则称为可完全优化规则; 当规则作用域中训练数据的数量小于C1时, 规则参数不存在唯一解, 使用求最小值方法获得的参数值容易使模型出现过拟合现象, 此时可采用减少规则未知量的方法避免过拟合。规则中评价等级置信度用于表示规则点处的推理值, 规则权重表示规则整体对作用域的影响程度, 前提属性权重表示规则中各前提属性的相对重要性, 规则权重与前提属性权重与不同规则之间或规则参数之间的相互关系有关。一般情况下, 专家对评价等级置信度赋值的精度较高, 对规则权重与前提属性赋值的精度相对较低, 因此设立临界值C2=1+M。当规则作用域中训练数据的数量小于C2且大于C1时, 将待优化参数调整为规则权重与前提属性权重, 处于该等级的规则称为可部分优化规则; 当训练数据数量小于C2时, 不再对规则进行优化, 位于此等级的规则称为不可优化规则。上述情况具体表示为:
| $ C(k) = \left\{ {\begin{array}{*{20}{l}} {{C_1},{C_1} \le {n_k}}\\ {{C_2},{C_2} \le {n_k} < {C_1}}\\ {0,{n_k} < {C_2}} \end{array}} \right. $ | (14) |
其中, C(k)为第k条规则需优化参数的数量, nk为第k条规则作用域中训练数据的数量。
4) 分级优化置信规则库提取所有已分级规则中待优化参数作为模型优化参数, 以模型输出与实际输出的最小差值作为目标函数, 利用粒子群算法优化模型参数, 计算公式为:
| $ \begin{array}{*{20}{l}} {\min \{ \xi (P)\} }\\ {\begin{array}{*{20}{l}} {{\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\theta _k} \le 1,{C_2} \le {\rm{C}}(k)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\delta _{i,k}} \le 1,{C_1} \le {\rm{C}}(k)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\beta _{i,k}} \le 1,{C_2} \le {\rm{C}}(k)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^N {{\beta _{i,k}}} = 1} \end{array}} \end{array} $ | (15) |
网络安全态势变化具有规律性, 在一定程度上可反映出攻击者的意图, 通常采用时间序列方法预测网络态势。基于分级优化置信规则库的网络安全态势预测由研究人员根据经验建立初始置信规则库模型, 再分级优化置信规则库, 具体过程如图 2所示。

|
Download:
|
| 图 2 基于HOBRB的网络安全态势预测流程 Fig. 2 Procedure of the network security situation prediction based on HOBRB | |
网络安全态势预测作为网络安全态势感知的第3个阶段, 需借助网络安全态势评估[10-12]生成所需的网络安全态势值。本文以某小型办公网络为实验对象验证本文方法的有效性, 并与其他网络安全态势预测方法进行对比来综合评价本文方法的效果。
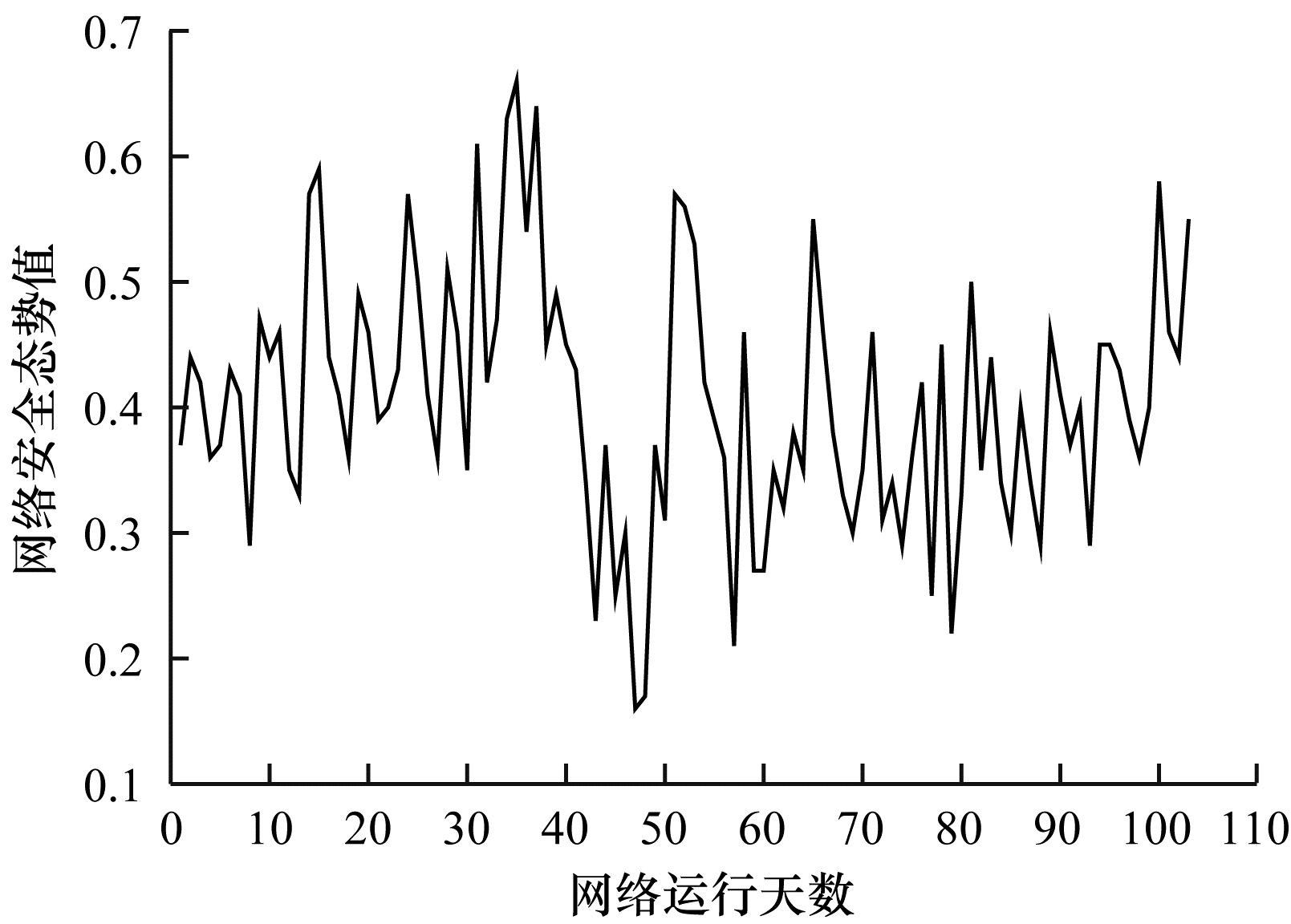
3.1 数据获取本文实验网络环境如图 3所示。其中, 网络安全评估设备用于识别网络违法行为并评估网络安全态势。网络安全态势评估周期为1天, 记录实验网络连续运行103天的网络安全态势值构成网络安全态势预测时间序列, 如图 4所示。

|
Download:
|
| 图 3 本文实验网络环境 Fig. 3 Experiment network environment of the proposed paper | |
|
Download:
|
| 图 4 网络安全态势序列 Fig. 4 Network security situation sequence | |
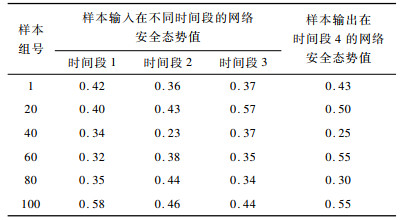
采用滑动窗口的方法[13](窗口处为1个时间段(连续的4天), 窗口每次向后滑动1天)生成100组样本数据(网络安全态势值)。选取前90组样本数据作为训练集, 后10组样本数据作为测试集。样本中输入部分为前3个时间段的网络安全态势值x(t-2)、x(t-1)和x(t), 输出部分为后1个时间段的网络安全态势值x(t+1)。部分样本的输入和输出如表 1所示。
|
下载CSV 表 1 部分样本的输入和输出 Table 1 Input and output of partial samples |
网络安全态势的取值范围为[0, 1], 由于网络安全状态较差时会造成网络瘫痪无法运行, 且通常网络中不存在绝对的安全状态[14], 因此本文将网络安全态势取值范围设置为[0.15, 0.80]。网络安全状态分安全(S)、低危(L)、中危(M)和高危(H)4个等级[15], 用态势参考值表示为[0.15, 0.36, 0.47, 0.80]。将置信规则库的输入属性数量设置为3, 建立初始置信规则库。
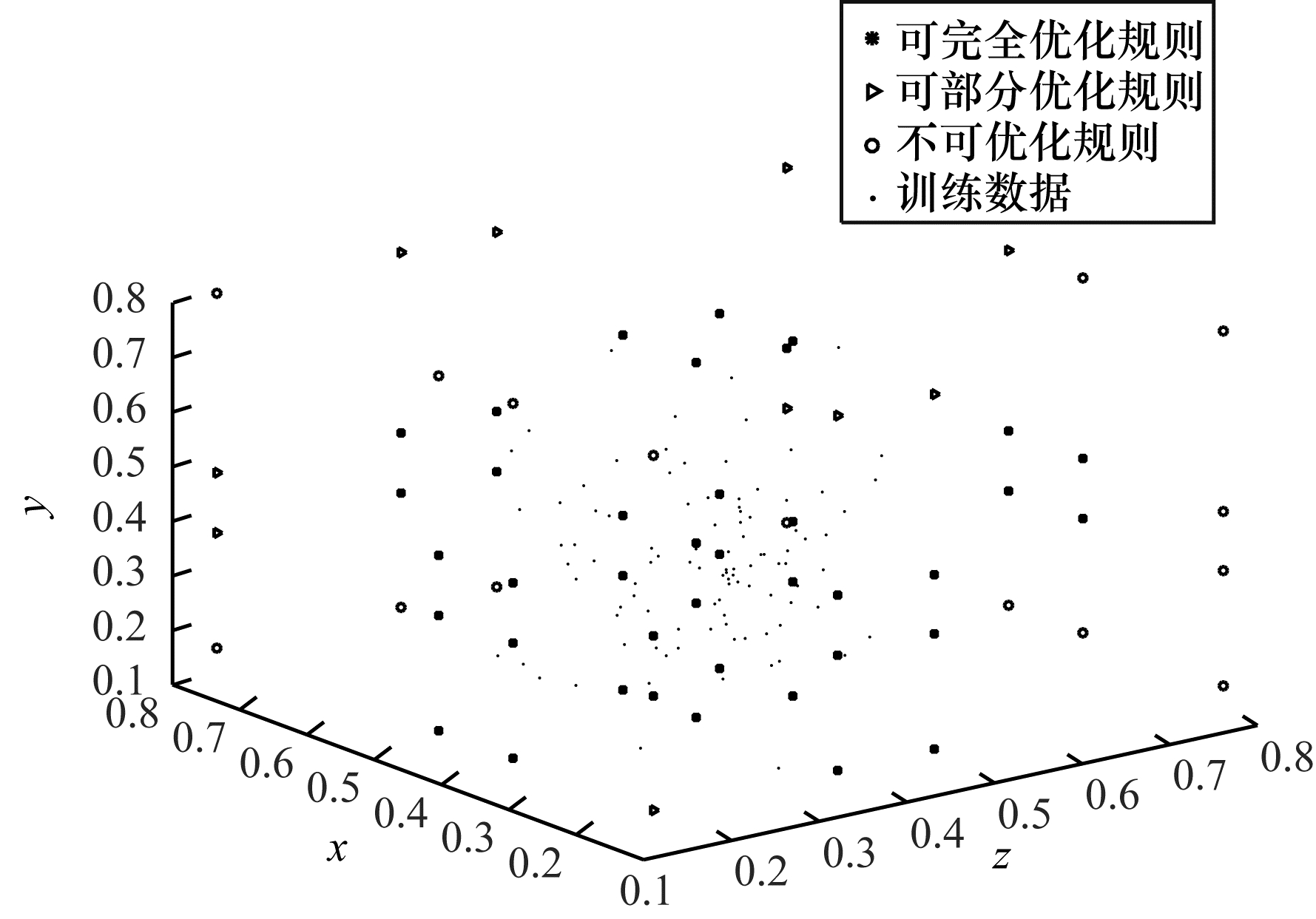
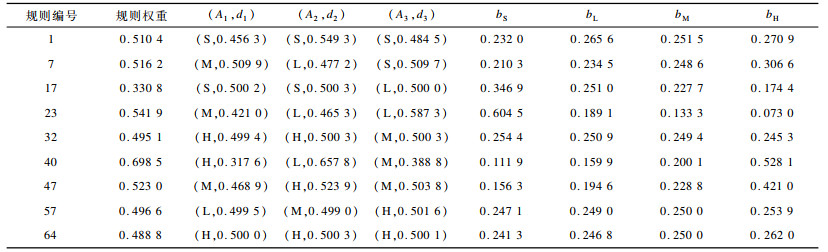
将置信规则库模型的作用域映射到三维空间, 划分规则作用域并将训练集数据分配到对应的规则作用域, 训练集数据分布情况与模型中各规则的激活状态如图 5所示。可以看出, 训练样本在模型作用域中间部位分布较密集, 而在边缘部位分布较稀疏。位于模型作用域中间部位的规则大部分处于可完全优化等级, 位于模型作用域边缘部位的规则大部分处于可部分优化等级或不可优化等级。经统计可知, 可完全优化等级包含39条规则, 可部分优化等级包含10条规则, 不可优化等级包含15条规则。使用分级优化方法后置信规则库的部分规则参数如表 2所示。
|
Download:
|
| 图 5 训练集数据分布与模型中各规则的激活状态 Fig. 5 Data distribution of training set and activation state of rules in the model | |
|
下载CSV 表 2 分级优化置信规则库的部分规则参数 Table 2 Partial rule parameters of HOBRB |
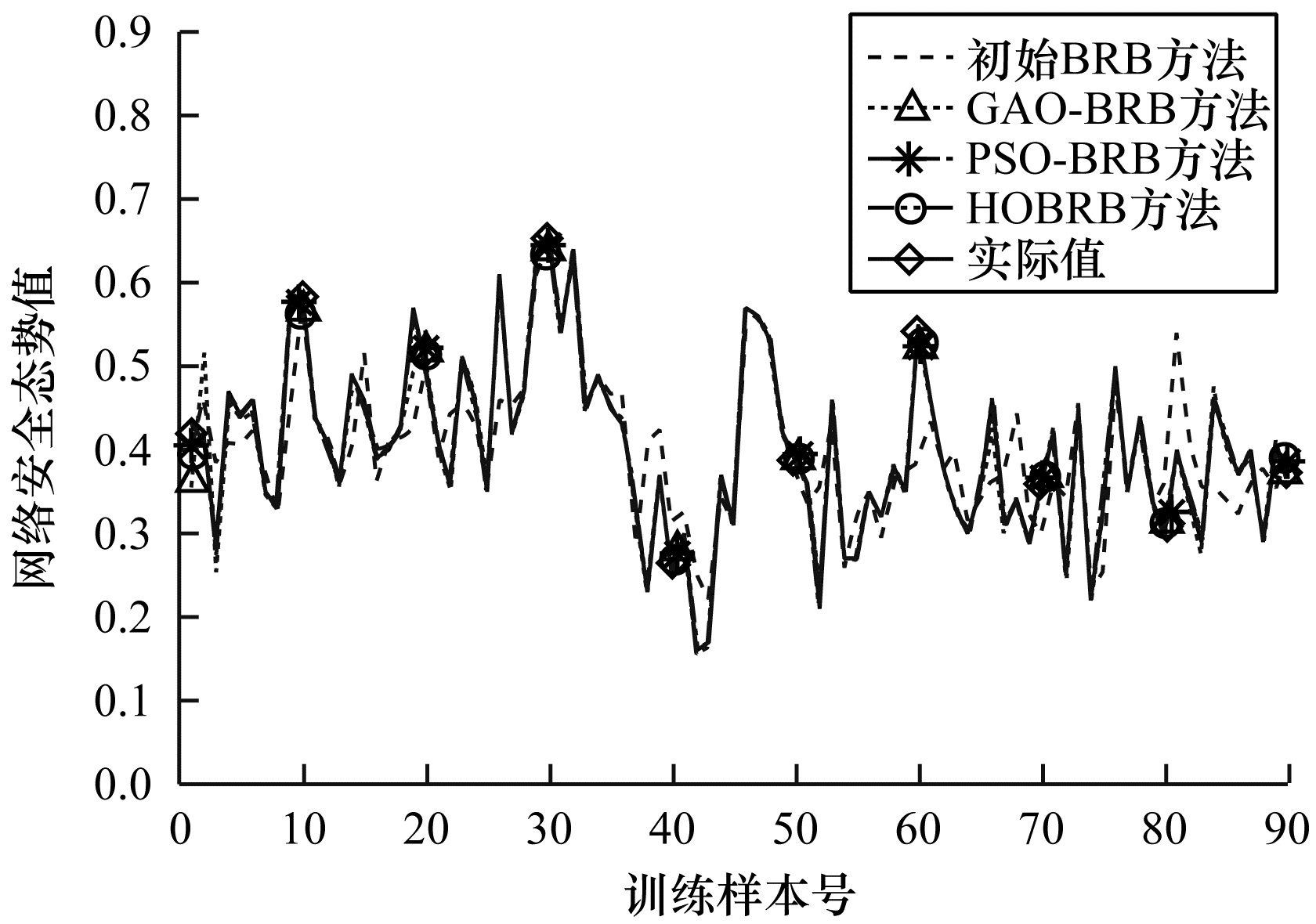
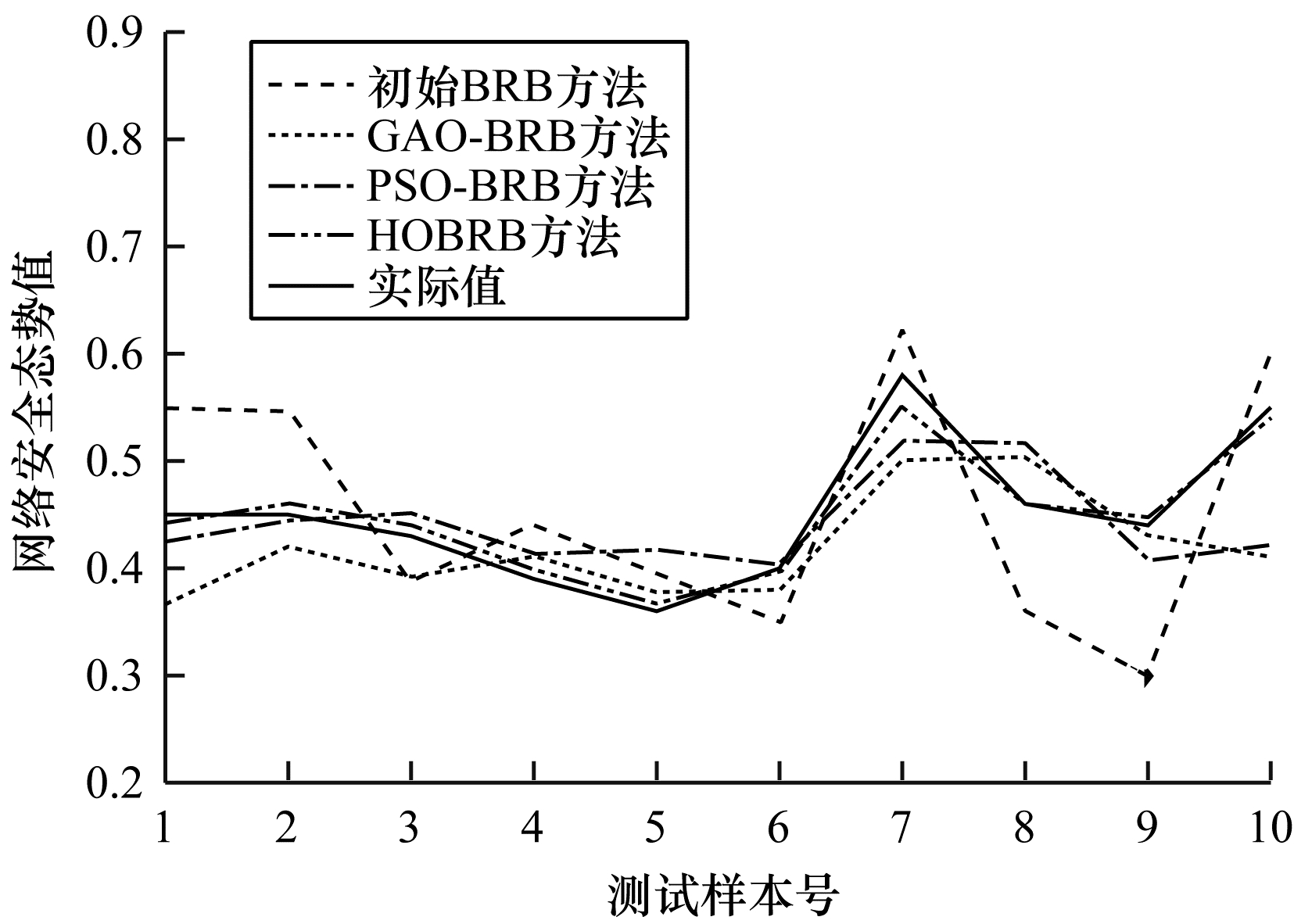
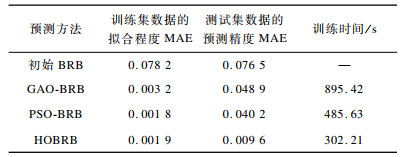
为综合检验本文方法, 分别建立基于初始置信规则库(初始BRB)、基于遗传算法[16-18]优化置信规则库(Genetic Algorithm Optimization Belief Rule Base, GAO-BRB)与基于粒子群[19-20]优化置信规则库(Particle Swarm Optimization Belief Rule Base, PSO-BRB)的网络安全态势预测方法, 将上述3种方法与本文提出的HOBRB方法对训练集数据的拟合程度、对测试集数据的预测精度以及训练时间进行对比。各方法所得训练集数据的拟合程度、测试集数据预测精度及其综合性能的对比情况分别如图 6、图 7和表 3所示(表 3中“—”表示未参与训练)。
|
Download:
|
| 图 6 不同方法对训练集数据的拟合程度对比 Fig. 6 Comparison of fitting degree of training set data from different methods | |
|
Download:
|
| 图 7 不同方法对测试集数据的预测精度对比 Fig. 7 Comparison of prediction accuracy of test set data from different methods | |
|
下载CSV 表 3 不同方法的综合性能对比 Table 3 Comprehensive performance comparison of different methods |
由上述模型的对比情况可知:优化过的BRB方法对训练集数据的拟合程度和测试集数据的预测精度整体上均优于初始BRB方法; 遗传算法易陷入局部最优导致GAO-BRB方法无法求得最优解且容易出现过拟合现象; 变速粒子群优化算法能改善粒子群算法的性能, 相对遗传算法优化速度更快, 且能有效避免算法求解时陷入局部最优, 但由于训练集数据分布不均, 因此导致PSO-BRB方法预测精度分布不均, 并存在过拟合现象; 分级优化算法受限于变速粒子群算法精度, 对训练样本的拟合程度与PSO-BRB方法相当, 但由于分级优化算法将规则划分为几个等级进行训练, 避免部分无法充分训练的规则参数的更改, 可有效避免HOBRB方法出现过拟合现象, 对测试集数据具有较好的预测精度, 且分级优化算法中待优化参数量更少, 可在一定程度上减少优化时间。
由于网络安全态势序列利用现有的网络安全态势评估工具[10-12]获取, 不可避免存在测量误差, 且由于存在网络攻击对象不确定性与攻击对象行为主观不确定性, 因此网络态势预测误差无法消除。然而网络态势变化在统计上存在规律性, 在整体上表现出可预测性, 通过将研究人员的定性经验知识与网络中采集的定量数据相结合可取得良好的预测效果, 为网络安全维护与升级提供参考。
4 结束语本文针对训练数据分布不均造成网络安全态势预测精度较低的问题, 提出一种利用分级优化置信规则库的预测方法。根据规则作用域中训练数据量与规则待求解参数量的关系划分规则优化等级, 对置信规则库进行分级优化, 在此基础上建立网络安全预测模型生成网络安全态势值。实验结果表明, 该方法能有效避免因训练数据分布不均造成的预测精度下降, 较GAO-BRB、PSO-BRB等预测方法的网络安全态势预测精度更高。后续将改进本文离子群参数优化算法, 进一步提高训练效率与预测精度。
| [1] |
LIU Xiaowu, YU Jiguo, LV Weifeng, et al. Network security situation:from awareness to awareness-control[J]. Journal of Network and Computer Applications, 2019, 139(8): 15-30. |
| [2] |
HU Guanyu.Research on network security situational awareness technology based on belif rule base[D].Harbin: Harbin University of Science and Technology, 2016.(in Chinese) 胡冠宇.基于置信规则库的网络安全态势感知技术研究[D].哈尔滨: 哈尔滨理工大学, 2016. |
| [3] |
YANG Jianbo, LIU Jun, XU Dongling, et al.Optimization models for training belief-rule-base systems[EB/OL].[2020-06-07].https://www.researchgate.net/publication/3412642_Optimization_Models_for_Training_Belief-Rule-Based_Systems.
|
| [4] |
CHANG Rui, BAI Yangsen, MENG Qingtao. Study on optimization of expert system learning of confidence rule base[J]. Journal of North China University of Water Resources and Hydropower (Natural Science Edition), 2015, 36(4): 72-78. (in Chinese) 常瑞, 白杨森, 孟庆涛. 置信规则库专家系统学习优化问题的研究[J]. 华北水利水电大学学报(自然科学版), 2015, 36(4): 72-78. |
| [5] |
YANG Hui, WU Peize, NI Jiliang. Parameter training algorithm based on improved particle swarm confidence rule base[J]. Computer Engineering and Design, 2017, 38(2): 400-404. (in Chinese) 杨慧, 吴沛泽, 倪继良. 基于改进粒子群置信规则库参数训练算法[J]. 计算机工程与设计, 2017, 38(2): 400-404. |
| [6] |
XU Xiaobin, ZHU Wei, XU Xiaojian, et al.Belief rule base optimization method based on parallel multi-population and redundant gene strategy[EB/OL].[2020-06-07].https://kns.cnki.net/kcms/detail/detail.aspx?dbcode=CAPJ&dbname=CAPJLAST&filename=MOTO20200313001&v=JCreBvAGjWiL6L7LmLbYh6Bho20ftQ1VkgX5HoO1dG9GPlKy3kmBcJO%25mmd2BYoD2gCmx.
|
| [7] |
YANG Jianbo. Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties[J]. European Journal of Operational Research, 2001, 131(1): 31-61. DOI:10.1016/S0377-2217(99)00441-5 |
| [8] |
YANG Jianbo, LIU Jun, WANG Jin, et al.Belief rule-base inference methodology using the evidential reasoning approach-RIMER[C]//Proceedings of 2006 IEEE Transactions on Systems, Man, and Cybernetics.Washington D.C., USA: IEEE Press, 2006: 266-285.
|
| [9] |
YANG Jianbo, XU Dongling.On the evidential reasoning algorithm for multiple attribute decision analysis under uncertainty[C]//Proceedings of 2006 IEEE Transactions on Systems, Man, and Cybernetics.Washington D.C., USA: IEEE Press, 2002: 289-304.
|
| [10] |
YANG Wenjun, ZHANG Jiaying, WANG Chundong, et al.Situation prediction of large-scale Internet of Things network security[EB/OL].[2020-06-07].https://www.researchgate.net/publication/335445182_Situation_prediction_of_large-scale_Internet_of_Things_network_security.
|
| [11] |
YAN Dingyu, LIU Feng, ZHANG Yaqin, et al. Dynamical model for individual defence against cyber epidemic attacks[J]. IET Information Security, 2019, 13(6): 541-551. DOI:10.1049/iet-ifs.2018.5147 |
| [12] |
BI Xinwen, SHI Xiaodan, ZHANG Zeliang. Cognitive machine learning model for network information safety[J]. Safety Science, 2019, 118(10): 435-441. |
| [13] |
SHANG Haixia, WEI Shoushui, LIU Feifei, et al.An improved sliding window area method for T wave detection[EB/OL].[2020-06-07].https://pubmed.ncbi.nlm.nih.gov/31065291/.
|
| [14] |
XI Rongrong, YUN Xiaochun, HAO Zhiyu. Framework for risk assessment in cyber situational awareness[J]. IET Information Security, 2019, 13(2): 149-156. |
| [15] |
TAO Xiaoling, LIU Yang, ZHAO Feng, et al.Graph database-based network security situation awareness data storage method[EB/OL].[2020-06-07].https://link.springer.com/article/10.1186/s13638-018-1309-9.
|
| [16] |
AIT W A, REKIK M, JABBOUR S. Cloud service composi-tion using minimal unsatisfiability and genetic algorithm[J]. Concurrency and Computation, 2020, 32(15): 1-13. |
| [17] |
YU Feng, XU Xiaozhong. A short-term load forecasting model of natural gas based on optimized genetic algorithm and improved BP neural network[J]. Applied Energy, 2014, 134(12): 102-113. |
| [18] |
GARG H. A hybrid PSO-GA algorithm for constrained optimization problems[J]. Applied Mathematics and Computation, 2016, 274(2): 292-305. |
| [19] |
DENG Wu, ZHAO Huimin, YANG Xinhua, et al. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment[J]. Applied Soft Computing, 2017, 59(10): 288-302. |
| [20] |
LIU Fang, ZHANG Jiawei, LIU Tong.A PSO-algorithm-based consensus model with the application to large-scale group decision-making[EB/OL].[2020-06-07].http://apps.webofknowledge.com/full_record.do?product=WOS&search_mode=GeneralSearch&qid=1&SID=8DP8BoWHTrreQKoPjpk&page=1&doc=1.
|
 2020, Vol. 46
2020, Vol. 46
