2. 教育部网络信息安全审计与监控工程研究中心, 上海 200433
2. Engineering Research Center of Cyber Security Auditing and Monitoring, Ministry of Education, Shanghai 200433, China
时间序列预测一直是国内外学者广泛关注的热点问题。精确的论坛发帖量预测是论坛流量生成的重要参考, 可以为网络流量规划、态势感知、舆情管理以及论坛用户行为模式分析等提供便利。针对时间序列预测, 研究人员提出了较多的单模型, 它们主要分为线性预测模型和非线性预测模型。线性预测模型中应用最广泛的是差分自回归移动平均(ARIMA)模型, 其在处理线性时间序列时具有优势, 但是不能预测非线性关系。非线性预测模型主要包括循环神经网络、长短期记忆(LSTM)神经网络、支持向量机和梯度提升树等, 这些模型具有较高的特征学习能力和非线性逼近能力, 在各种时间序列预测任务中取得了较好的效果, 但是它们容易陷入局部最小值并产生过拟合现象。
目前, 对于网络论坛、微博和贴吧等社交媒体的流量预测, 多数研究人员使用长短期记忆网络[1-2]、卷积神经网络[3]和径向基神经网络[4]等非线性预测模型, 非线性预测模型的关键部分在于特征工程[5]。除历史时间序列数据之外, 在对微博发帖模式的预测中, 学者们主要使用用户资料特征、微博类型以及语义特征。在对微博删除量的预测上, 文献[6]使用用户关注数、内容长度等特征。对于股吧论坛发帖量的预测, 基于用户信息的特征与论坛发帖量的相关性不高, 而股吧子论坛对应的股票价格涨幅、论坛关注数和新闻提及度等为可用的重要特征。特征工程通常需要预测者丰富的相关知识以及与时间序列相关的大量信息, 而可选择的特征数据规模大、维度复杂并且提取难度高。例如, 股票的新闻提及度特征通常很难提取, 复杂程度很高。除此之外, 在实际应用中, 能得到的关于时间序列的信息往往很少, 可选择的特征通常只有历史时间序列。
集成模型综合不同模型的优点, 具有较高的预测准确性和稳定性。目前, 模型集成方式主要分为3种。第1种是对时间序列的不同部分分别建模预测后将每部分的预测结果进行集成[7-9], 文献[10]使用离散小波变换得到时间序列的线性和非线性结构, 使用差分自回归移动平均模型和神经网络分别对两部分实现建模预测并将结果进行组合。第2种是利用子模型优化最终模型参数[11-12], 文献[11]利用模拟退火回溯搜索算法优化反向传播神经网络参数以获得更优的预测结果。第3种是利用多种子模型对整条时间序列进行预测, 最后集成各子模型的预测结果。目前, 对于多模型预测结果的集成主要有算术平均法、加权平均法以及基于模型的集成法[13-14]3种方式。基于算术平均的集成方法往往受子模型预测结果中极端值的影响而产生误差, 利用基于测试集RMSE的加权平均法[15-16]对子模型进行集成需要利用时间序列的真实值, 而利用训练集RMSE的加权平均法[17-19]容易产生过拟合问题从而导致实验结果出现较大的偏差, 同时训练过程中对极端值的拟合偏差将对模型最终权重造成影响。
在仅利用历史时间序列作为特征的情况下, 本文提出一种基于多模型集成的论坛流量预测模型。为解决上述模型集成方式中存在的问题, 本文集成模型参照加权投票法的思想, 在每一个时间尺度下, 依据各模型预测值所在区间的密度大小赋予各模型不同的权重, 然后通过加权平均得到最终的预测结果, 从而避免过拟合问题并降低极端值对预测结果的影响。
1 子模型的选择本文选用ARIMA、LSTM、Prophet以及梯度提升决策树(GBDT)4个子模型, 这4个模型都是当前比较流行、基于不同方法的时间序列预测模型, 且在数学原理、长短期精度以及对时间序列信息的提取和适用方面各不相同。
ARIMA模型是以统计学和数学随机过程理论为基础的时间序列分析方法, 其优点是模型简单、时间复杂度低、短期预测精度高。但是, ARIMA模型的建模过程需要将非平稳时间序列转化为平稳时间序列, 该过程会损失一部分非线性信息, 因此, 其难以很好地处理非线性数据的拟合问题, 且长期预测精度较低。
Prophet[20]是以时间序列分解和曲线拟合思想为基础而建立的模型, 其时间复杂度较低、建模简单。与ARIMA模型相比, Prophet的优点是对节假日和突发事件造成的数据波动具有很好的拟合效果, 并能在一定程度上拟合非线性数据, 适用于长期且周期明显的时间序列预测。但是, Prophet在趋势、周期不明显的时间序列预测中效果不佳。
线性模型难以捕获时间序列中的非线性数据, 机器学习方法在训练过程中能够自动从数据中学习隐含关系, 对非线性数据有强大的学习能力。因此, 在ARIMA和Prophet模型的基础上, 本文选用机器学习模型LSTM和GBDT。
LSTM是一种循环神经网络, 具有定向循环的特点, 可以很好地分析时间序列前后之间相互关联的预测问题。LSTM的优点是可以较好地拟合时间序列中的非线性数据, 且模型能存储时间序列中长时间信息, 可以提取到时间序列中间隔和延迟相对较长的重要信息。因此, LSTM对时间序列的趋势预测和长期预测精度较高。但是, LSTM模型较为复杂, 时间和计算复杂度高, 训练一个简单的LSTM模型也需要耗费较长的时间。此外, LSTM容易陷入局部最小点, 还存在泛化性能不高的问题。
GBDT是基于集成学习而建立的时间序列预测模型, 其本质是一种迭代的决策树算法, 每次迭代建立的模型都在之前模型损失函数的梯度下降方向。GBDT同样可以较好地拟合线性和非线性数据, 对时间序列的长期和短期预测精度都较高。与LSTM模型相比, GBDT模型的时间和计算复杂度更低, 泛化程度更高。
2 集成模型集成是建立一系列模型, 通过策略性地将其组合在一起以获得准确性更高、稳定性更佳、泛化效果更好的模型。在对时间序列进行预测时, 通常没有一个可以适用于所有时间序列的模型, 每个模型都有其适用的范围和优缺点。为了达到较好的预测效果, 研究人员通常要尝试多个模型和多种参数。集成可以通过组合单模型来降低选择错误模型的风险, 同时较大限度地利用各子模型预测结果的信息, 从而解决单模型由于随机因素影响导致的预测值误差大的问题, 最终提高预测性能。
要获得性能较好的集成模型, 各子模型应该具有一定的准确性, 同时子模型之间需要存在差异, 否则集成模型的效果不会优于子模型。本文选取ARIMA、LSTM、GBDT以及Prophet 4个子模型, 4个模型的基本原理以及运用的算法各不相同, 在长短期精度、适用范围方面各有所长。
加权投票法是一种集成学习的方法, 投票结果往往可以使子模型之间的预测结果互补, 以此降低单个子模型的预测误差。本文算法采用加权投票法的思想, 通过多数投票和加权平均对各子模型产生的预测结果进行集成。在对时间序列进行预测时, 无法从预测结果中判断各子模型的预测性能。为了比较子模型的预测效果, 本文借鉴“投票”的思想, 让多个子模型进行“投票”。基于“投票”的思想, 可以认为多数子模型的预测值所在区间是与真实值更加接近的区间, 该区间称为密集区间。
当每个子模型都具有一定的准确性时, 假设子模型i的错误率为εi, 在t时刻时间序列真实值为ft, 设子模型i的预测值为Si(t), 则子模型i的预测值接近真实值的概率为:
| $ P\left( {{S_i}(t) = \left( {{f_t} \pm \delta } \right)} \right) = 1 - {\varepsilon _i} $ | (1) |
其中, δ是一个可允许的误差范围。为了便于说明, 本文假设共有a个子模型, 每个子模型的错误率均为ε且错误率相互独立, 则各子模型在(ft±δ)内形成密集区间的概率PD为:
| $ {P_{\rm{D}}} = \sum\limits_{q = 2}^a {\left( {\begin{array}{*{20}{l}} a\\ q \end{array}} \right)} {(1 - \varepsilon )^q}{\varepsilon ^{a - q}} = 1 - \left( {{\varepsilon ^a} + a(1 - \varepsilon ){\varepsilon ^{a - 1}}} \right) > 0 $ | (2) |
从式(2)可以看出, 密集区间存在且预测值位于密集区间的子模型更接近真实值, 错误率更低。因此, 赋予预测值位于密集区间的子模型一个高的权重, 可以提高预测精度。为了证明这一点, 使用算术平均模型的错误率和集成模型的错误率进行对比。假设子模型的错误率分别为ε1, ε2, …, εa, 算术平均模型的错误率为
| $ \begin{array}{l} \Delta \varepsilon = w\left( {\frac{{{\varepsilon _1} + {\varepsilon _2} + \cdots + {\varepsilon _b}}}{b}} \right) + (1 - w) \cdot \\ \;\;\;\;\;\;\;\left( {\frac{{{\varepsilon _{b + 1}} + {\varepsilon _{b + 2}} + \cdots + {\varepsilon _a}}}{{a - b}}} \right) - \frac{{{\varepsilon _1} + {\varepsilon _2} + \cdots + {\varepsilon _a}}}{a} = \\ \;\;\;\;\;\;\;\left( {w - \frac{b}{a}} \right)(a - b)b\left( {\frac{{{\varepsilon _1} + {\varepsilon _2} + \cdots + {\varepsilon _b}}}{b} - } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{{\varepsilon _{b + 1}} + {\varepsilon _{b + 2}} + \cdots + {\varepsilon _a}}}{{a - b}}} \right) \end{array} $ | (3) |
其中, (a-b)b是一个常数。预测值位于密集区间的子模型的平均错误率小于非密集区间的模型平均错误率, 则
综上, 当选取适当的权重时, 赋予预测值位于密集区间的子模型一个高的权重可以提高预测精度。
本文选用4个子模型, 可能会产生投票数相同的情况。因此, 添加算术平均模型作为第5个子模型, 即在使用4个子模型对时间序列分别预测后, 对4个子模型的预测结果进行算术平均, 得到算术平均模型, 将其作为第5个子模型, 从而避免投票数相同的情况发生。
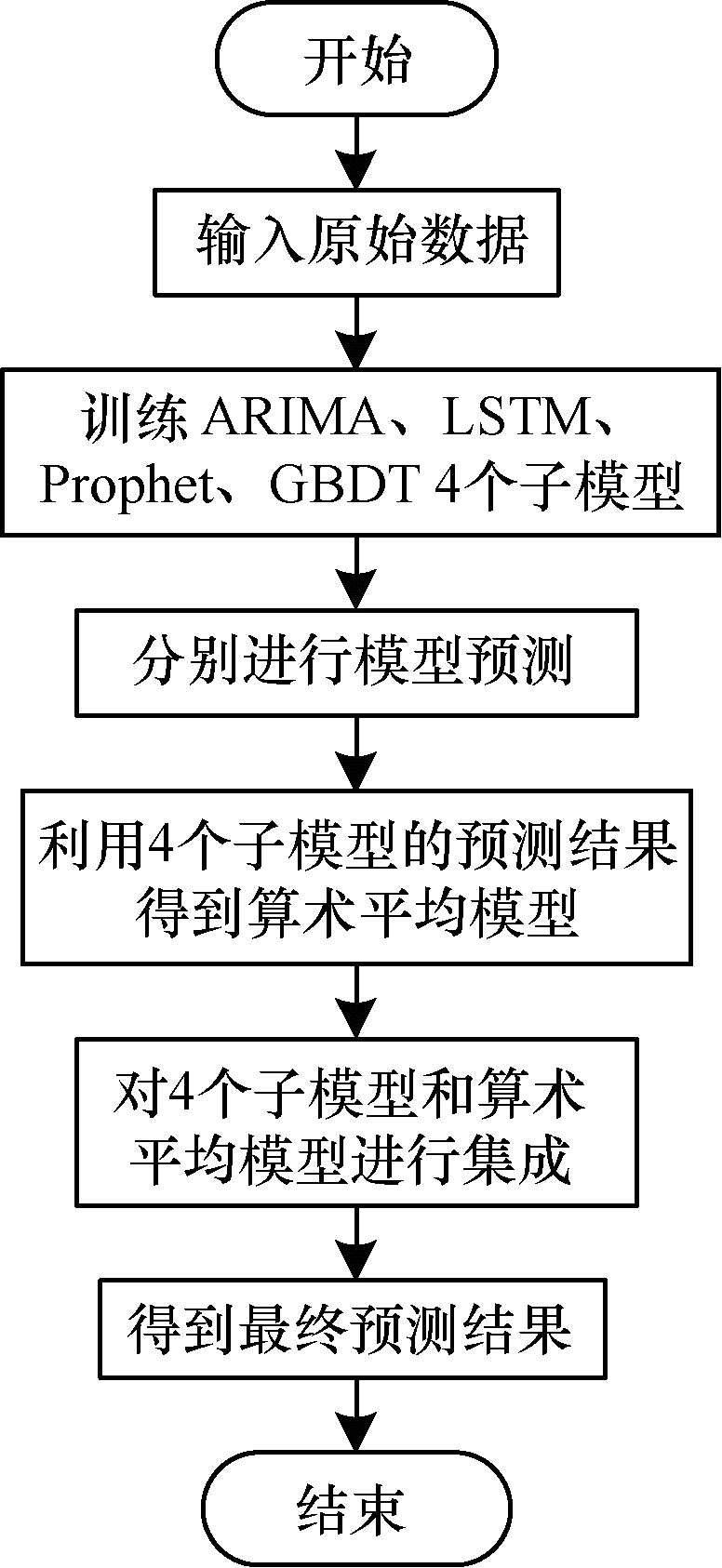
在时间尺度单位下, 各子模型进行“投票”, 选出密集区间, 然后赋予预测值位于密集区间的子模型更大的权重, 赋予预测值不在该区间的子模型较小的权重, 从而降低子模型预测结果中的极端值对集成结果的影响, 最终预测结果即为各子模型预测结果与子模型在该时间的权重的乘积之和。集成模型流程如图 1所示。
|
Download:
|
| 图 1 集成模型流程 Fig. 1 Procedure of the integrated model | |
各子模型的权重与子模型预测结果是否位于密集区间有关, 即密集区间的范围将对最终预测结果产生影响。本文设定一个参数k来控制区间的范围。在某一时刻, 当子模型A与子模型B之间预测值距离小于预设的k值时, 认为模型A与模型B的预测值位于同一区间。将各子模型预测值进行排序, 然后遍历每个预测值并依据k值划分区间。多数子模型预测值所在的区间为密集区间, 对这些子模型赋予较大的权重, 对预测值不在密集区间的子模型赋予较小的权重。最后, 通过加权平均的方法得到最终预测值。
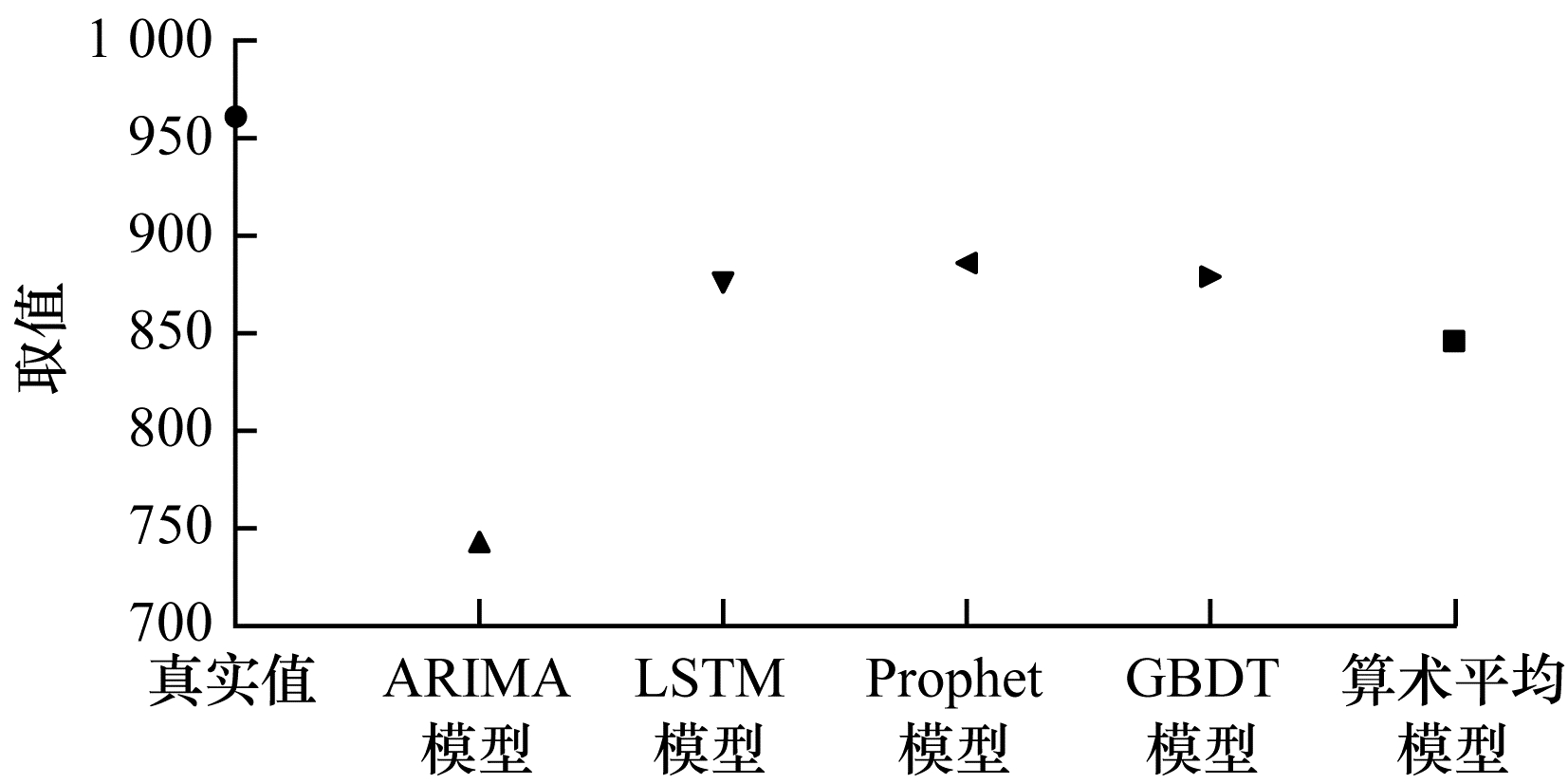
图 2所示为5个子模型对2018年8月17日股吧论坛发帖量的预测值。从图 2可以看出, 当k值取28时, LSTM、Prophet以及GBDT 3个子模型的预测值位于同一区间且该区间为密度最大的区间, 表明当日真实值最有可能位于此区间。因此, 赋予这个区间的3个子模型预测值较大的权重, 并对预测值不在该区间的ARIMA模型和算术平均模型赋予较小的权重, 从而降低此时间尺度单位下ARIMA模型和算术平均模型预测值过小对最终结果产生的影响, 提高预测精度。
|
Download:
|
| 图 2 子模型预测值对比 Fig. 2 Comparison of predicted values of submodels | |
综上, 本文集成模型算法描述如下:
输入 时间序列X=[X1, X2, …, Xn], 其中, n为训练集大小。
输出 集成多个子模型预测结果的最终预测值Y=[Y1, Y2, …, Ym], 其中, m为预测的时间长度。
步骤1 分别利用ARIMA、LSTM、Prophet、GBDT 4个模型对原始时间序列进行建模, 将训练集数据X=[X1, X2, …, Xn]输入模型并训练模型。
步骤2 分别对4个子模型进行预测。由于4个子模型均为目前流行的时间序列预测模型, 本文不对子模型的具体算法进行详细阐述, 下面主要介绍子模型的具体预测方式。
1) 使用ARIMA模型进行单步预测, 然后将模型单步预测生成的结果作为输入进行滚动预测。ARIMA模型在t时刻的输入为时间序列X和t时刻之前模型生成的所有预测结果, 输出为S0(t)。数学表达式如下:
| $ {S_0}(t) = {\mathop{\rm ARIMA}\nolimits} \left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_2}, \cdots ,{\mathit{\boldsymbol{X}}_n} + \sum\limits_{{t^\prime } = 1}^{t - 1} {{S_0}} \left( {{t^\prime }} \right)} \right) $ | (4) |
2) 使用LSTM模型进行输入步长为timestep的单步预测, 再将模型单步预测生成的结果作为输入进行滚动预测。则在t时刻LSTM模型的输入为部分时间序列Xn-timestep+(t-1), Xn-timestep+(t-1)+1, …, Xn和t时刻之前模型生成的所有预测结果, 输入步长为timestep, 输出为S1(t)。数学表达式如下:
| $ \begin{array}{l} {S_1}(t) = {\mathop{\rm LSTM}\nolimits} \left( {{\mathit{\boldsymbol{X}}_{n - {\rm{ timestep }} + (t - 1)}},{\mathit{\boldsymbol{X}}_{n - {\rm{timestep }} + (t - 1) + 1}}, \cdots } \right.,\\ \;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{X}}_n} + \sum\limits_{{t^\prime } = 1}^{t - 1} {{S_1}} \left( {{t^\prime }} \right)} \right) \end{array} $ | (5) |
3) 使用Prophet模型进行预测。Prophet模型基于曲线拟合的思想, 使用整条时间序列X作为输入训练模型后直接输出t时刻的预测结果S2(t)。数学表达式如下:
| $ {S_2}(t) = {\mathop{\rm Prophet}\nolimits} \left( {{\mathit{\boldsymbol{X}}_1},{\mathit{\boldsymbol{X}}_2}, \cdots ,{\mathit{\boldsymbol{X}}_n}} \right) $ | (6) |
4) 与LSTM的预测方法类似, 使用GBDT模型进行输入步长为timestep的单步滚动预测。其在t时刻的预测方法和输入与LSTM模型相同, 输出为S3(t)。数学表达式如下:
| $ \begin{array}{l} {S_3}(t) = {\rm{ GBDT }}\left( {{\mathit{\boldsymbol{X}}_{n - {\rm{timestep}} + (t - 1)}},{\mathit{\boldsymbol{X}}_{n - {\rm{timestep}} + (t - 1) + 1}}, \cdots \mathit{\boldsymbol{,}}} \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{X}}_n} + \sum\limits_{{t^\prime } = 1}^{t - 1} {{S_3}} \left( {{t^\prime }} \right)} \right) \end{array} $ | (7) |
综上, 可以得到预测值集合Si, i=0, 1, 2, 3, 其中, i为子模型编号。
步骤3 对4个子模型的预测值Si, i=0, 1, 2, 3进行算术平均, 得到第5个子模型, 即算术平均模型S4:
| $ {S_4} = \frac{{\sum\limits_{i = 0}^3 {{S_i}} }}{4} $ | (8) |
步骤4 在t时刻, 对5个子模型的预测值进行升序排列并遍历。若2个子模型在时间t的预测值Si(t)与Sj(t)之间距离小于等于k值, 将预测值Si(t)和Sj(t)加入集合Dtx中, Dtx是t时刻各子模型的一个密度区间, x为该区间的序号。
若其他子模型在时间t的预测值Sl(t)与集合Dtx内任一值的距离小于等于k值, 则将Sl(t)加入集合Dtx中; 反之, 将其加入新的集合Dtx+1中, Dtx+1为不同于Dtx的新密度区间, 依此类推。
在t时刻, 对于5个子模型的预测结果进行排序的时间复杂度为O(alb a), a为子模型个数; 对排序后的值进行遍历并划分区间的时间复杂度为O(a)。则在t时刻, 集成算法的时间复杂度为O(alb a)。
步骤5 对于每个时间尺度t, 可以得到包含预测值最多的集合Dtmax, 其中, max为该集合的编号。对于预测值属于Dtmax的子模型赋予权重w(w>0.5);对于预测值不属于Dtmax的子模型赋予权重1-w。则在t时刻子模型i的权重可以表示为:
| $ {w_i}(t) = \left\{ {\begin{array}{*{20}{l}} {w,i \in D_t^{\max }}\\ {1 - w,i \notin D_t^{\max }} \end{array}} \right. $ | (9) |
步骤6 利用加权平均的方法得到最终的t时刻集成模型预测值Yt为:
| $ {\mathit{\boldsymbol{Y}}_t} = \sum\limits_{i = 0}^4 {{w_i}} (t){S_i}(t) $ | (10) |
其中, Si(t)表示子模型i在t时刻的预测值。
对于一段时间长度, 集成算法的时间复杂度为O(malb a)。
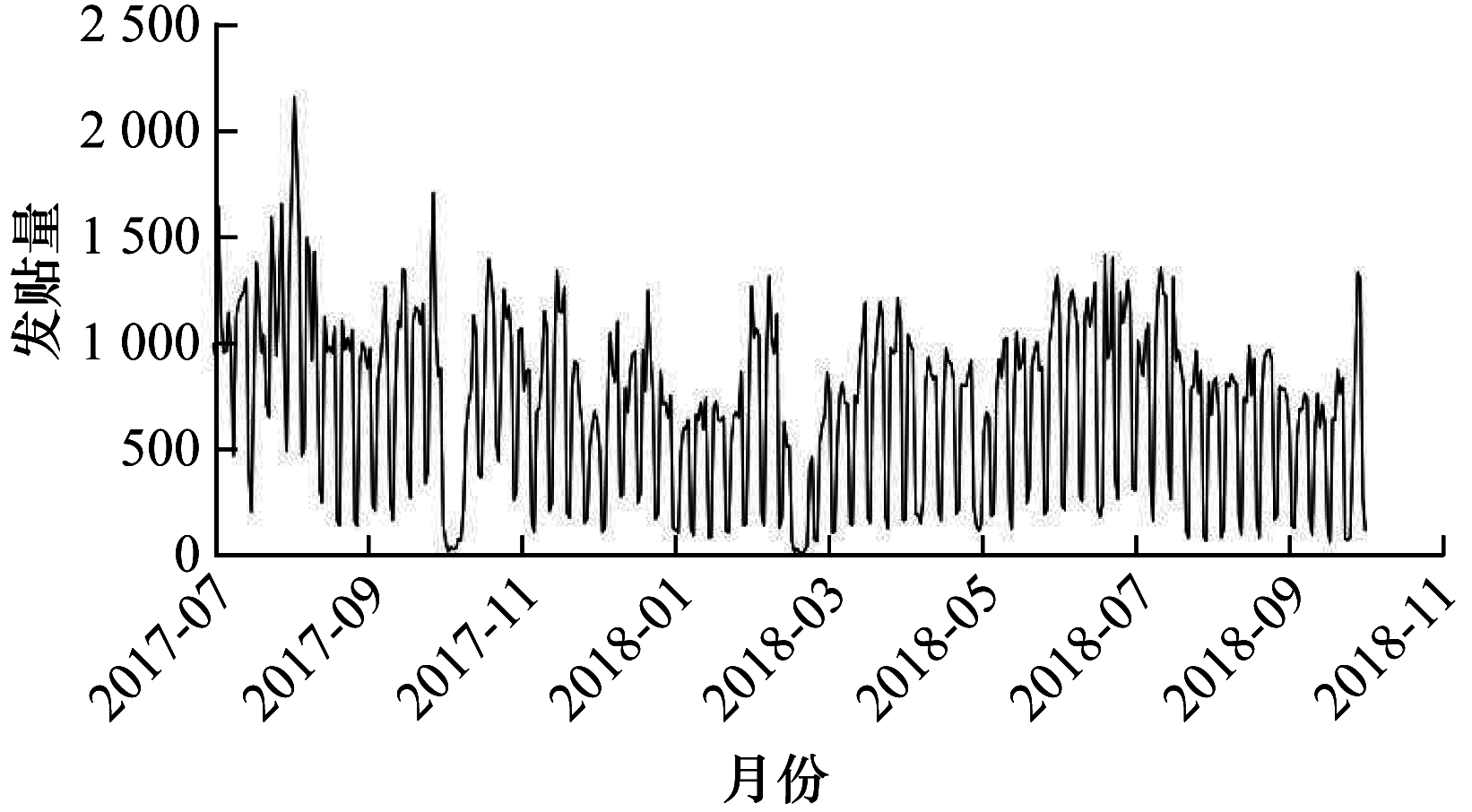
3 实验结果与分析本文实验数据集包含股吧论坛所有子论坛从2017年7月1日—2018年9月30日的每日发帖量数据, 共457条。将2017年7月1日—2017年8月15日的发帖量作为测试集, 依据不同的算法建立子模型以预测2017年8月16日—2018年9月28日的发帖量, 并与实际情况相比较。股吧论坛发帖量的时间序列如图 3所示, 可以看出, 股吧论坛发帖量的时间序列具有周和年2种周期性。
|
Download:
|
| 图 3 股吧论坛发帖量的时间序列 Fig. 3 Time series of the number of posts on Guba | |
在数据集预处理时对数据集中的缺失项进行中位数插值。此外, 2018年9月27日与9月28日两天受国庆节放假影响, 数据量偏高, 因此, 在分析结果时删除这2条异常数据。
模型的预测性能评价指标使用均方根误差RMSE和相对误差δ。RMSE和δ的计算公式分别如式(11)、式(12)所示:
| $ {{\mathop{\rm RMSE}\nolimits} = \sqrt {{{\left( {{f_t} - {y_t}} \right)}^2}} } $ | (11) |
| $ {\delta = \frac{{\sum\limits_{t = 1}^m {\left| {{f_t} - {y_t}} \right|} }}{{\sum\limits_{t = 1}^m {{f_t}} }}} $ | (12) |
其中, ft为时间序列真实值, yt为预测值。
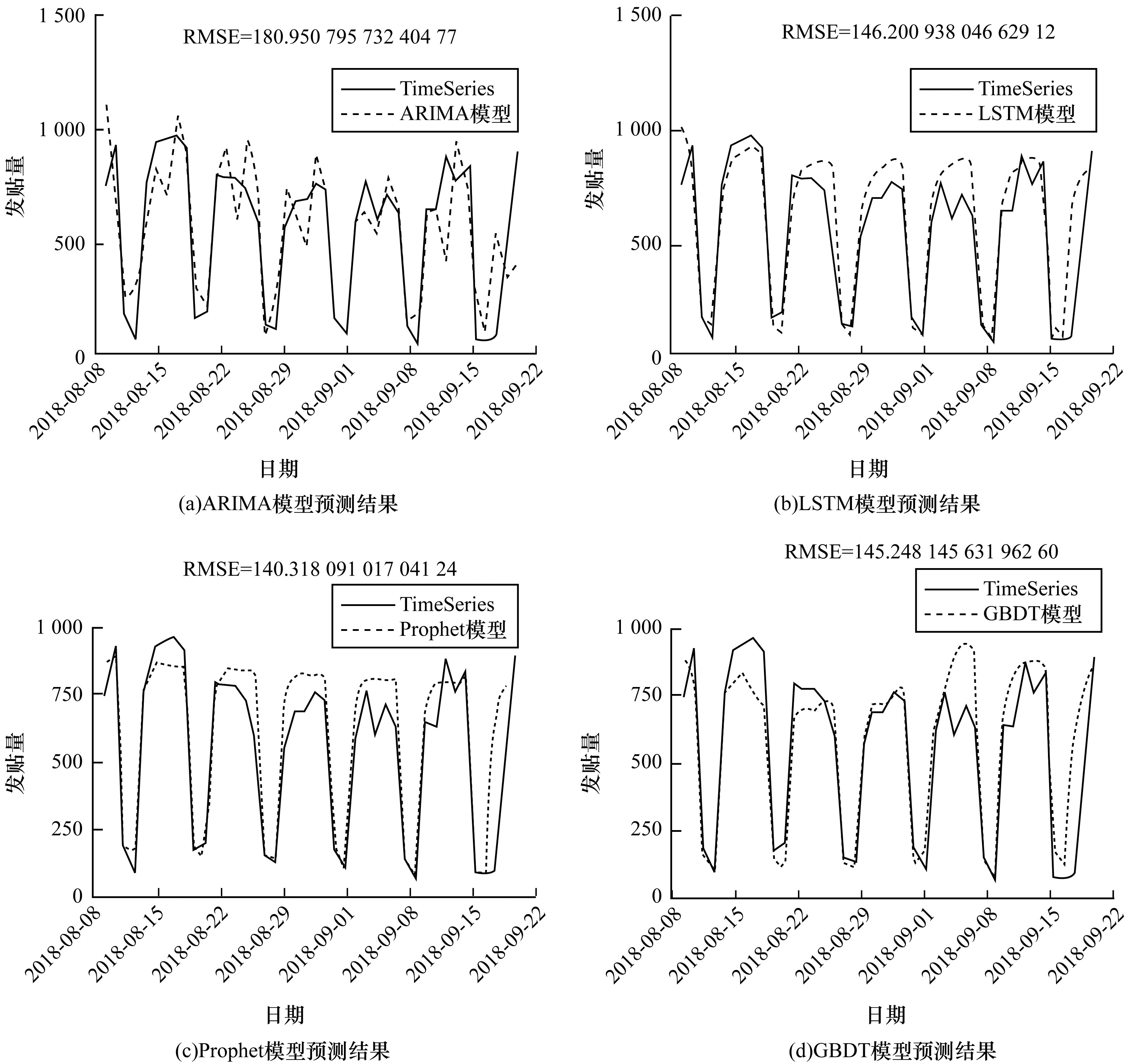
3.1 股吧论坛发帖量预测分别利用ARIMA、LSTM、Prophet和GBDT 4个模型对原始时间序列进行预测。4个子模型的预测结果与原始时间序列的对比如图 4所示, 其中, TimeSeries表示原始时间序列。
|
Download:
|
| 图 4 4个子模型的预测结果 Fig. 4 Prediction results of four submodels | |
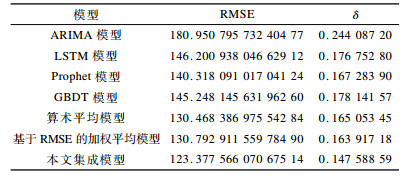
从图 4可以看出, 4个子模型均具有一定的准确性, LSTM、Prophet以及GBDT 3个模型在预测效果上差别较小。使用算术平均法、基于RMSE的加权平均法和本文集成算法分别对4个子模型进行集成。集成模型使用网格搜索得到最优参数, 各子模型和不同集成模型的结果对比如表 1所示。
|
下载CSV 表 1 子模型及集成模型的实验结果1 Table 1 Experimental results 1 of submodels and integrated models |
从表 1可以看出, 所有集成模型均获得了比子模型更好的预测结果。对比不同的集成模型可以看出, 本文集成模型得到的RMSE和相对误差值比其他2种集成模型更小。对于基于RMSE的加权平均模型而言, 使用测试集的RMSE需要利用时间序列的真实值, 利用训练集的RMSE容易产生过拟合问题从而导致实验结果出现较大偏差。在各模型预测结果的RMSE值相差不大时, 使用基于RMSE的加权平均法的效果甚至低于简单的算术平均法。而本文模型参考加权投票法的思想, 认为多数模型预测值所在的区间应当更接近真实值。从实验结果可以看出, 在选择合适的区间大小和权重比例时, 本文模型能获得比其他2种集成模型更优的预测效果。
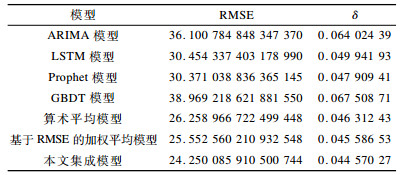
3.2 不同模式的时间序列集成效果为了验证本文集成模型的泛化性, 将各种对比模型应用于国际航班乘客数时间序列, 该序列与股吧论坛发帖量模式不同, 结果如表 2所示。
|
下载CSV 表 2 子模型及集成模型的实验结果2 Table 2 Experimental results 2 of submodels and integrated models |
与股吧论坛发帖量数据集结果类似, 本文集成模型对国际航班乘客数数据集进行建模后, 预测结果的RMSE和相对误差值低于算术平均模型和基于RMSE的加权平均模型, 这表明本文集成模型对于不同的时间序列具有一定泛化性。
3.3 不同k值和权重比例对集成结果的影响k值的选取以及不同密度区间的权重比例是影响本文集成模型预测结果的重要因素。本次实验使用网格搜索来确定最佳的k值和权重比例。
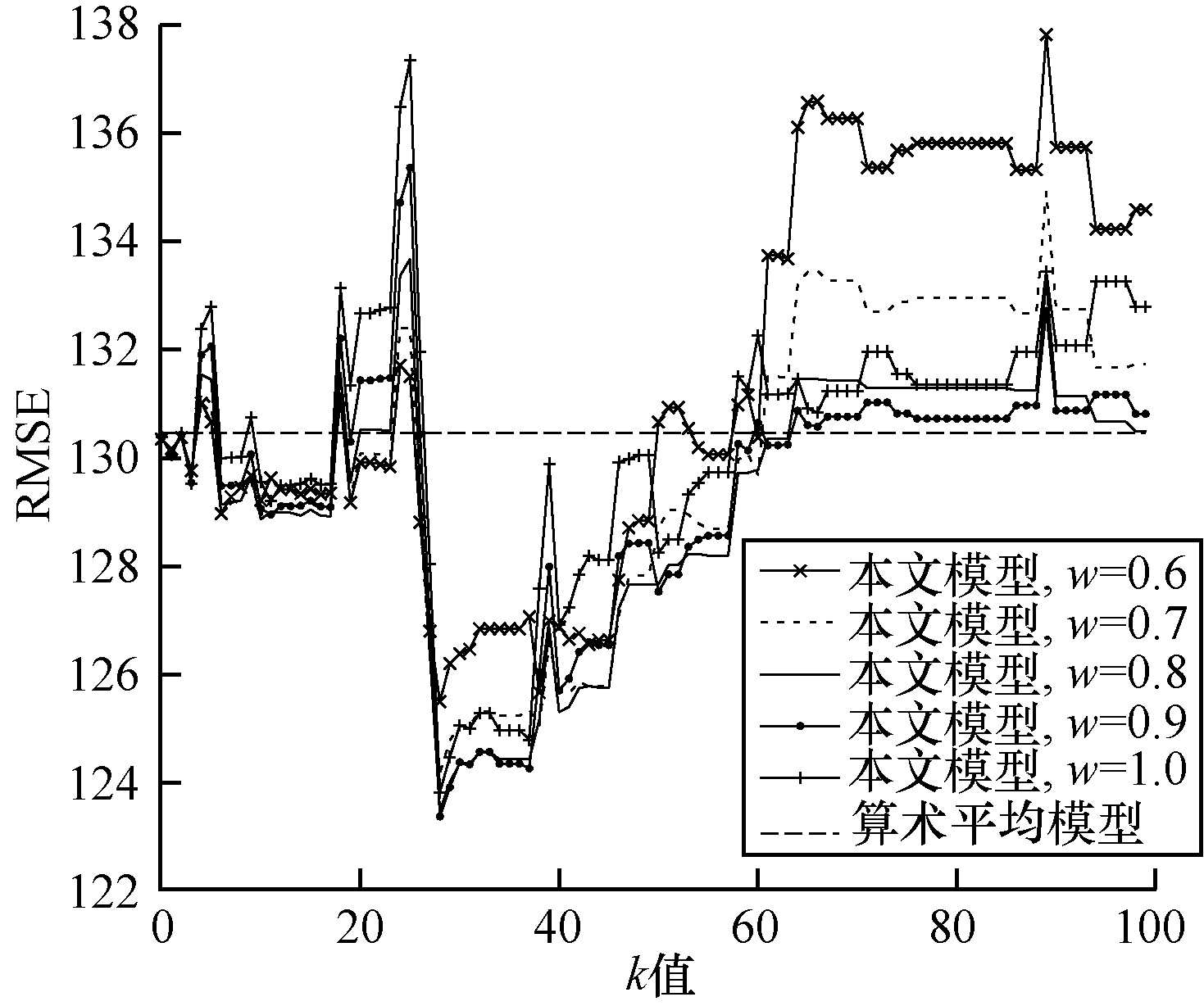
为了验证不同k值和权重比例对时间序列的影响, 选用不同的权重比例, k取[0, 100]内的所有整数, 对股吧论坛发帖量数据集进行实验, 并将预测结果的RMSE与算术平均模型得到的RMSE进行对比, 结果如图 5所示。从图 5可以看出, 在模型k值固定的情况下, 不同权重比例之间的RMSE值波动幅度较小; 而当模型的权重比例固定时, 不同k值之间的RMSE值波动幅度较大。因此, k值对实验结果的影响大于权重比例。在实验过程中选择合适的权重比例, 可以在一定程度上减小子模型预测中极端值对最终预测结果的影响, 而k值将影响集成模型对预测结果的优化效果。从实验结果可以看出, 选择k=28、w=0.9时可以获得最佳预测结果。
|
Download:
|
| 图 5 不同k值和权重比例时的集成模型预测结果 Fig. 5 Prediction results of integrated models with different k values and weight ratios | |
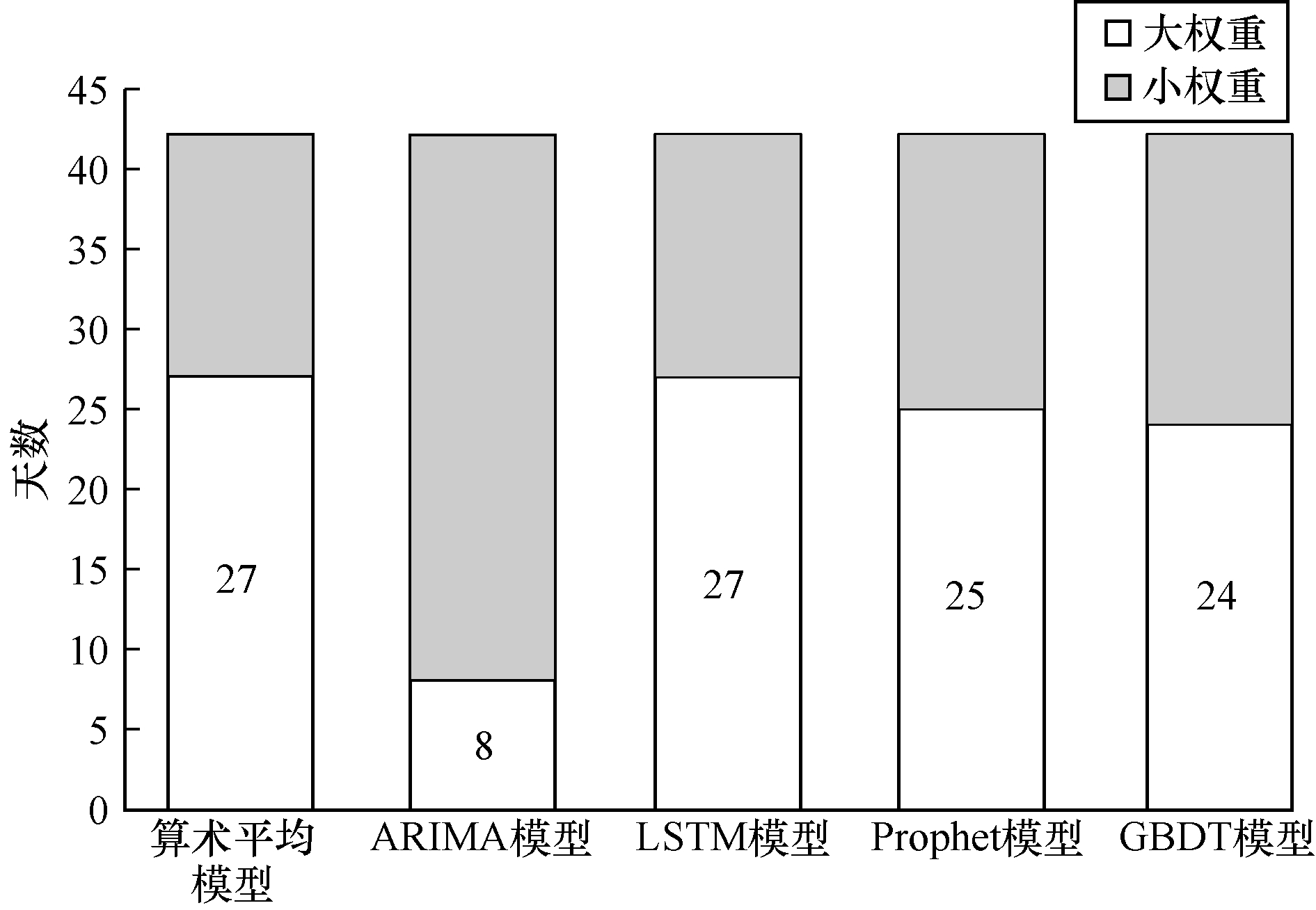
在预测结果最佳的情形下, 统计各子模型未来42天的预测值分别被赋予大权重和小权重的天数, 结果如图 6所示。
|
Download:
|
| 图 6 各模型被赋予大、小权重的天数统计 Fig. 6 Statistics of days when each model is given large and small weights | |
4个子模型被赋予大、小权重的天数比例能从一定程度上说明4个子模型的准确率大小。从图 6可以看出, 算术平均模型、LSTM模型、Prophet模型和GBDT模型的预测值被赋予大权重的天数大致相同, 表明LSTM、Prophet以及GBDT这3个子模型的准确率相近, 而ARIMA模型的预测值被赋予大权重的天数较低, 表明其准确率略低于其他3个子模型。该实验结果与4个子模型RMSE值的差距吻合, 表明本文模型倾向于赋予RMSE值更高的子模型一个大权重, 以此提高模型的预测精度。针对ARIMA模型准确率较低的问题, 今后将对子模型的个数和类型选择进行探究, 以获得精度更高的集成模型。
LSTM模型由于对极端值预测结果偏差较大导致其RMSE值略高于Prophet和GBDT模型, 但是在实验过程中, LSTM模型被赋予大权重的天数多于其他子模型, 表明LSTM模型对于非极端值的预测较为准确。与基于RMSE值的加权平均模型相比, 使用本文算法对4个子模型进行集成, 可以在一定程度上避免单模型在极端值上的预测偏差对模型最终权重造成的影响。
4 结束语本文建立一种基于多模型集成的网络论坛流量预测模型。通过ARIMA、LSTM、Prophet和GBDT 4个模型分别对时间序列进行预测, 在时间尺度单位下参照加权投票法的思想, 使各子模型投票选出密集区间, 依据各模型预测值所在区间的密度大小赋予各模型不同的权重, 然后进行加权平均得到最终的预测结果。实验结果表明, 与算术平均模型、基于RMSE的加权平均模型相比, 该模型预测结果的RMSE值与相对误差值更小, 且对于不同模式的时间序列具有一定的泛化性。
本文集成模型的最终预测结果依据各子模型的投票而产生, 无需预测该时间段的真实数据且避免了模型在训练集上过拟合而导致的实验结果偏差问题。同时, 本文模型通过合理的权重分配降低了预测过程中极端值对预测结果的影响。各子模型的投票区间k值以及权重分配w值的选取非常重要, 下一步将对k值和w值的取值范围和选取规则进行深入研究。此外, 在已有研究的基础上适当增加和调整子模型, 分析子模型的类型和个数对预测结果精度的影响也是今后的研究方向。
| [1] |
YANG Haiming, PAN Zhisong, TAO Qing.Robust and adaptive online time series prediction with long short-term memory[EB/OL].[2019-09-20].http://downloads.hindawi.com/journals/cin/2017/9478952.pdf.
|
| [2] |
KRSTANOVIC S, PAULHEIM H.Ensembles of recurrent neural networks for robust time series forecasting[M].Berlin, Germany: Springer, 2017.
|
| [3] |
GAO Hongchang, KONG Deguang, LU Miao, et al.Attention convolutional neural network for advertiser-level click-through rate forecasting[C]//Proceedings of 2018 World Wide Web Conference.New York, USA: ACM Press, 2018: 1855-1864.
|
| [4] |
XIAO Ding, LI Xu, LIN Xiuqin, et al.A time series prediction method based on self-adaptive RBF neural network[C]//Proceedings of the 4th International Conference on Computer Science and Network Technology.Washington D.C., USA: IEEE Press, 2015: 147-189.
|
| [5] |
GAO Xiaofeng, CAO Zhenhao, LI Sha, et al. Taxonomy and evaluation for microblog popularity prediction[J]. ACM Transactions on Knowledge Discovery from Data, 2019, 13(2): 1-40. |
| [6] |
BAGDOURI M, OARD D W.On predicting deletions of microblog posts[C]//Proceedings of the 24th ACM International Conference on Information and Knowledge Management.New York, USA: ACM Press, 2015: 1707-1710.
|
| [7] |
LIU Z T, YAN, HAUSKRECHT M.A flexible forecasting framework for hierarchical time series with seasonal patterns[C]//Proceedings of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval.New York, USA: ACM Press, 2018: 889-892.
|
| [8] |
HYNDMAN R J, AHMED R A, ATHANASOPOULOS G, et al. Optimal combination forecasts for hierarchical time series[J]. Com putational Statistics & Data Analysis, 2011, 55(9): 2579-2589. |
| [9] |
MADAN R, MANGIPUDI P S.Predicting computer network traffic: a time series forecasting approach using DWT, ARIMA and RNN[C]//Proceedings of 2018 International Conference on Contemporary Computing.Washington D.C., USA: IEEE Press, 2018: 1-5.
|
| [10] |
KHANDELWAL I, ADHIKARI R, VERMA G. Time series forecasting using hybrid ARIMA and ANN models based on DWT decomposition[J]. Procedia Computer Science, 2015, 48: 173-179. DOI:10.1016/j.procs.2015.04.167 |
| [11] |
LI Huiyuan, PAN Lian, CHEN Mei, et al.RBM-based back propagation neural network with BSASA optimization for time series forecasting[C]//Proceedings of the 9th International Conference on Intelligent Human-Machine Systems and Cybernetics.Washington D.C., USA: IEEE Press, 2017: 16-22.
|
| [12] |
WEI Dengfeng. Network traffic prediction based on RBF neural network optimized by improved gravitation search algorithm[J]. Neural Computing and Applications, 2017, 28(8): 2303-2312. DOI:10.1007/s00521-016-2193-z |
| [13] |
KIM W, GOYAL B, CHAWLA K, et al. Attention-based ensemble for deep metric learning[M]. Berlin, Germany: Springer, 2018.
|
| [14] |
LI Yuelong, TANG Dehua, JIANG Guiyuan, et al. Short term traffic flow forecasting based on dimension weighted residual LSTM[J]. Computer Engineering, 2019, 45(6): 1-5. (in Chinese) 李月龙, 唐德华, 姜桂圆, 等. 基于维度加权的残差LSTM短期交通流量预测[J]. 计算机工程, 2019, 45(6): 1-5. |
| [15] |
QIU X H, ZHANG L, REN Y, et al.Ensemble deep learning for regression and time series forecasting[C]//Proceedings of 2014 IEEE Symposium on Computational Intelligence in Ensemble Learning.Washington D.C., USA: IEEE Press, 2014: 159-168.
|
| [16] |
CHOI J Y, LEE B.Combining LSTM network ensemble via adaptive weighting for improved time series forecasting[EB/OL].[2019-09-20].http://downloads.hindawi.com/journals/mpe/2018/2470171.pdf.
|
| [17] |
RUAN Wenjie, SHENG Quan, XU Peipei, et al.Forecasting seasonal time series using weighted gradient RBF network based autoregressive model[C]//Proceedings of the 25th ACM International Conference on Information and Knowledge Management.New York, USA: ACM Press, 2016: 2021-2024.
|
| [18] |
AKYUZ A O, UYSAL M, BULBUL B A, et al.Ensemble approach for time series analysis in demand forecasting: ensemble learning[C]//Proceedings of 2017 IEEE International Conference on Innovations in Intelligent Systems and Applications.Washington D.C., USA: IEEE Press, 2017: 195-203.
|
| [19] |
DENG Lujia, LIU Pingshan. Research on click-through rate prediction of advertisement based on GMM-FMs[J]. Computer Engineering, 2019, 45(5): 122-126. (in Chinese) 邓路佳, 刘平山. 基于GMM-FMs的广告点击率预测研究[J]. 计算机工程, 2019, 45(5): 122-126. |
| [20] |
TAYLOR S J, BENJAMIN L.Forecasting at scale[EB/OL].[2019-09-20].https://peerj.com/preprints/3190.pdf.
|
 2020, Vol. 46
2020, Vol. 46

 ,
,