2. 上海第二工业大学 计算机与信息工程学院, 上海 201209
2. School of Computer and Information Engineering, Shanghai Polytechnic University, Shanghai 201209, China
面向服务计算和面向服务体系架构的推广和应用[1], 促进了Web服务的发展。Web服务具有完全开放、松散耦合、具备标准协议和高度可集成等特征[2], 基于Web服务技术[3]并采用开放的可扩展标记语言定义的服务, 能够摆脱对平台的依赖, 实现服务重组, 动态满足用户的服务需求, 并且节约资源和时间。随着大数据时代的到来, Web服务数量剧增, 涌现出很多功能相似但非功能属性即服务质量(Quality of Service, QoS)不同的服务。如何在不同QoS的候选服务集合中高效实现服务的选择和组合, 使得组合服务能够满足客户的功能和非功能需求, 是一个典型的NP难题[4]。
近年来, 针对基于QoS感知的Web服务组合问题, 国内外学者提出了各种改进的启发式算法, 获得了近似最优解。文献[5-6]通过融合其他方法来改进遗传进化(Genetic Evolutionary, GA)算法。其中:文献[5]借助模拟退火以及和声搜索算法改进GA算法的交换策略; 文献[6]通过对候选服务集局部选优的方式缩小搜索空间, 提升GA算法性能。由于粒子群优化(Particle Swarm Optimization, PSO)算法参数少、收敛速度快, 因此文献[7-8]对其改进后用于解决服务组合问题:文献[7]通过迭代生成的余切序列扰乱粒子的运动速度和位置, 提升PSO算法的全局搜索能力; 文献[8]通过优化PSO算法的惯性权重和学习参数的方式提升算法的寻优能力, 但PSO算法普遍存在“早熟”现象, 易陷入局部最优解。文献[9-10]提出一种基于差分进化(Differential Evolution, DE)算法的服务组合方法:文献[9]通过一种新型的编码方式提高算法的寻优能力, 但算法在大规模组合服务情况下性能较差; 文献[10]通过引入结构知识, 提出基于知识的差分进化(Knowledge-based DE, KDE)算法, 加快了算法的收敛速度。针对大规模服务组合问题, 文献[11-12]将人工蜂群(Artificial Bee Colony, ABC)算法应用于Web服务组合优化:文献[11]通过精英策略增强搜索能力; 文献[12]采用一种受差分进化启发的搜索策略提高搜索效率。此外, 文献[13]提出一种扩展的花朵授粉(Extended Flower Pollination Algorithm, EFPA)算法, 在花朵授粉算法的基础上引入GA算法的变异和交换策略, 进一步提升了算法性能。
本文提出一种改进的花朵授粉(Improved FPA, IFPA)算法用于优化Web服务组合。将差分进化算法的变异和交换操作加入到花朵授粉算法中, 增强花朵的有效性和多样性, 并利用贪心策略选择适应度值高的花朵, 从而加快算法收敛速度, 增强算法寻优能力, 提高组合服务性能。
1 Web服务组合问题 1.1 QoS感知的Web服务组合针对客户提出的服务需求, 可将需求抽象为n种功能不同的子任务T=(t1, t2, …, tn)。在执行子任务ti时, 可从相关候选服务集Si=(si1, si2, …, sim)中选择服务sij来完成相应子任务。服务sij包含k种QoS属性Qij=(qij1, qij2, …, qijk), 最后生成组合服务CS=(s1j1, s2j2, …, snjn), ji∈{1, 2, …, m}, 其QoS属性满足客户所提出的要求。
工作流管理联盟(WFMC)提出的顺序(Sequence)、循环(Circular)、选择(Selective)和并行(Parallel)4种工作流管理模型结构, 可支持Web服务组合建模, 其中, 并行、选择和循环3种基本模型均可转化为顺序类型。为便于讨论, 本文只讨论顺序模型。
1.2 QoS属性值及其归一化本文引入QoS属性计算组合服务的适应度值, 用于评价Web服务组合的非功能特性。具体可选取Web服务的可靠性(rel)和可用性(ava)这两种效益型属性和响应时间(rtm)、价格(cos)这两种成本型属性来描述服务质量[14]。
Web服务不同的QoS属性具有不同的衡量方式, 因此, 在计算组合服务的适应度之前必须对QoS属性值进行预处理。本文借鉴文献[10]方法对QoS进行归一化操作, 计算公式如下:
| $ q_{ij}^{k\prime } = \left\{ {\begin{array}{*{20}{l}} {\frac{{\max \left( {q_i^k} \right) - q_{ij}^k}}{{\max \left( {q_i^k} \right) - \min \left( {q_i^k} \right)}},k \in \{ {\rm{rtm}},\cos \} }\\ {\frac{{q_{ij}^k - \min \left( {q_i^k} \right)}}{{\max \left( {q_i^k} \right) - \min \left( {q_i^k} \right)}},k \in \{ {\rm{rel}},{\rm{ ava }}\} } \end{array}} \right. $ | (1) |
其中, qijk表示第i个任务第j个候选服务的第k个QoS属性值, qik表示完成第i个任务任一候选服务的第k个QoS属性值。
1.3 QoS聚合函数不同服务的QoS属性具有不同的特性, 其对应的QoS聚合函数也有所不同, 本文借鉴文献[15], 采取累和及累积两种操作。
组合服务的响应时间和价格属性通过原子服务累和而成, 聚合函数如下:
| $ {Q_k} = \sum\limits_{i = 1}^n {q_i^k} ,k \in \{ \cos ,{\rm{rtm}}\} $ | (2) |
组合服务的可用性和可靠性属性通过其原子服务累积而成, 聚合函数如下:
| $ {Q_k} = \prod\limits_{i = 1}^n {q_i^k} ,k \in \{ {\rm{ava}},{\rm{ rel}}\} $ | (3) |
通过加权求和的方式计算组合服务CS的服务质量, 服务组合优化的数学模型可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {y = \max \left( {{Q_{{\rm{cs}}}}} \right)}\\ {{Q_{{\rm{cs}}}} = \sum {{w_k}} {Q_k}}\\ {{Q_k} \le {C_k}} \end{array}} \right. $ | (4) |
其中, n为服务组合中任务的个数, Qk为组合服务的某种QoS属性值, Ck为这种QoS属性的约束条件, wk为第k种QoS属性在总服务质量中所占权重,
花朵授粉算法(FPA)由YANG等人于2012年提出, 其是一种新型的元启发式群智能优化算法。FPA模拟植物界中花朵授粉的方式, 主要有自花授粉和异花授粉两种方式[16]。该算法通过转换概率实现局部搜索和全局搜索的动态转换, 平衡两者之间的关系。FPA按照以下规则进行设计:
1) 花朵的异花授粉被视为全局搜索, 传粉者飞行传粉服从Levy分布。
2) 花朵的自花授粉被视为局部搜索。
3) 花朵的常性是指两朵相近的花朵更易授粉, 可以认为是一种繁衍概率, 与两朵花之间的相似度成比例。
4) 局部授粉和全局授粉的动态转换由概率p控制。
在异花授粉(全局搜索)过程中, 传粉者通过Levy飞行机制进行传粉, 其寻优演化可表示为:
| $ x_i^{t + 1} = x_i^t + L\left( {{\rm{gBest}} - x_i^t} \right) $ | (5) |
其中, xit为第t代种群中第i朵花的位置, gBest为当前最优解, L为服从Levy分布的随机变量。L的计算公式如下:
| $ L\sim\frac{{\lambda \Gamma (\lambda )\sin ({\rm{ \mathit{ π} }}\lambda /2)}}{{\rm{ \mathit{ π} }}} \times \frac{1}{{{s^{1 + \lambda }}}},0 < {s_0} < < s $ | (6) |
其中, λ=1.5, Γ(λ)为标准伽马函数。
自花授粉(局部搜索)在花朵附近区域进行搜索, 可表示为:
| $ x_i^{t + 1} = x_i^t + \varepsilon \left( {x_j^t - x_k^t} \right),i \ne j \ne k $ | (7) |
其中, ε为[0, 1]之间的随机数。
2.2 IFPA算法的差分进化机制差分进化(DE)算法是一种基于群体的进化方法[17], 包括初始化、变异、交换、选择等步骤。DE算法流程简单, 易于实现[18-19]。
研究表明, 标准的花朵授粉算法存在一些缺陷, 如收敛速度慢、在高维情况下易早熟、全局搜索能力差等。针对上述不足, 本文将差分进化算法的变异、交换操作加入到花朵授粉算法中, 以增强花朵的有效性和多样性, 并利用贪心策略选择适应度值高的花朵, 以加快算法收敛速度, 增强FPA算法的寻优能力。
2.2.1 变异操作FPA基于种群Xt=(x1t, x2t, …, xNt)寻优, 通过差分变异操作引入种群全局信息和个体局部信息, 进一步提升搜索能力, 增加种群的多样性。在t代种群中, 第i个个体是xit=(xi, 1t, xi, 2t, …, xi, nt), 其中, n是子任务的个数。通过式(8)处理xit, 得到新个体vit, 即:
| $ \mathit{\boldsymbol{v}}_i^t = \mathit{\boldsymbol{x}}_{{r_1}}^t + \delta \left( {\mathit{\boldsymbol{x}}_{{r_2}}^t - \mathit{\boldsymbol{x}}_{{r_3}}^t} \right) $ | (8) |
其中, i≠r1≠r2≠r3且i, r1, r2, r3∈[1, N], δ为缩放因子, δ∈(0, 1)。
2.2.2 交换操作为提高种群的多样性, 利用原向量xit和变异个体vit进行交叉操作, 生成新的个体uit:
| $ u_{i j}^{t}=\left\{\begin{array}{l} v_{i j}^{t}, C_{\mathrm{rand}}<\mathrm{CR} \text { 或 } j=\text { unidrand }(N) \\ x_{i j}^{t}, \text { 其他 } \end{array}\right. $ | (9) |
其中, uijt、vijt和xijt为t代种群中第i个个体在j维上的值, Crand为(0, 1)之间的随机数, CR为(0, 1)之间的交叉概率, unidrand(N)为[1, N]之间的随机整数。最后得到新种群Ut。
2.2.3 选择操作为加快算法的收敛速度, 直接将种群Xt和变异、交换后的种群Ut混合, 依据贪心策略, 按适应度值选取N个花朵个体组合成新的种群Xt+1。
2.3 服务组合建模 2.3.1 编码方式本文采用整数编码方式表示离散的服务, 利用一个整数数组S=(s1, s2, …, sn)表示服务组合的一个解决方案(即一个花粉或花朵), 将寻找最优组合服务问题转化为向量S求最优解问题, 其中, 每个整数si都代表相应任务中选择的候选服务索引的序列号。计算每个花粉S的适应度值, 对该花粉所对应的服务组合方案进行评估, 判断组合服务的优劣。
2.3.2 适应度函数适应度函数作为Web服务组合评估函数, 计算方法有很多, 为便于比较, 本文根据服务组合优化数学模型, 对于按式(2)累和的属性进行取平均数操作, 对于按式(3)累积的属性进行开方操作, 最终使适应度函数的值介于(0, 1)之间。同时, 借鉴文献[1]引入罚函数来构造适应度函数, 将约束优化问题转变为无约束优化问题, 实现全局最优化。综合考虑本文所选取的QoS属性, Web服务组合的适应度函数值fitness表示如下:
| $ \begin{array}{l} {\rm{ fitness }} = {\sum\limits_{k \in \mid \cos ,{\rm{rtm}}\} }}{w_k}\frac{{{Q_k}}}{n} + \sum\limits_{k \in \left\{ {{\rm{ava}},{\rm{rel}}} \right\}} {{w_k}} \sqrt[n]{{{Q_k}}}{f_q} - \lambda \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{k \in \{ \cos ,{\rm{rtm}},{\rm{ava}},{\rm{rel}}\} } {{{\left( {\frac{{\Delta {Q_k}}}{{Q_k^{\max } - Q_k^{{\rm{min}}}}}} \right)}^2}} \end{array} $ | (10) |
其中, λ为惩罚系数, Qkmax为对k属性的最大约束值, Qkmin为对k属性的最小约束值。
| $ \Delta {Q_k} = \left\{ {\begin{array}{*{20}{l}} {Q_k^{\min } - {Q_k},{Q_k} \le Q_k^{\min }}\\ {0,Q_k^{\min } < {Q_k} < Q_k^{\max }}\\ {{Q_k} - Q_k^{\max },{Q_k} \ge Q_k^{\max }} \end{array}} \right. $ | (11) |
本文将提出的IFPA算法应用于服务组合优化问题, 该算法的具体步骤如下:
步骤1 初始化参数, 初始化种群规模N、最大迭代次数tmax、转换概率p、最小缩放因子δ和交叉概率CR。
步骤2 初始化种群, 并根据适应度函数计算当前种群适应度值, 记录全局最优值及其对应的最优解。
步骤3 如果转化概率p < rand(0, 1)成立, 则进行全局搜索, 根据式(5)对解进行更新, 并做越界处理。
步骤4 如果转换概率p>rand(0, 1)成立, 则进行局部搜索, 根据式(7)对解进行更新, 并做越界处理。
步骤5 计算步骤3或步骤4新生成的花朵适应度值, 并与原花朵个体的适应度值进行比较, 如果新的个体适应度值更高, 则用新个体替换旧个体, 同时记录整个种群的最优值和最优解, 最终得到新种群Xt。
步骤6 利用DE算法中的式(8)对整个种群进行变异操作, 并对变异后的种群Vt做越界处理。
步骤7 利用DE算法中的式(9)对种群Xt和变异种群Vt进行交换操作, 得到最终的新种群Ut, 并计算新种群Ut中每个个体的适应度值。
步骤8 从种群Xt和种群Ut中按贪心策略选取适应度较高的N个花朵个体, 组成新的第(t+1)代种群Xt+1, 并更新全局最优值和最优解。
步骤9 判断结束条件, 如果满足, 则退出并输出最优值和对应的最优解, 否则转步骤3。
3 实验与结果分析 3.1 实验环境和数据通过仿真实验, 验证IFPA算法对基于QoS感知的Web服务组合优化的有效性, 分别从可行性和收敛性2个方面对IFPA、KDE[13]和EFPA[14]3种服务组合优化算法, 以及DE和FPA 2种传统优化算法进行比较。实验环境为:Windows 10, 64位操作系统, 英特尔Core i7-7700HQ@2.80 GHz四核处理器, 8 GB内存。
实验选用2个不同的数据集D1和D2。数据集D1是由ZENG等人提供的QWS数据集[20-21], 该数据集收录了互联网中2 507个Web服务, 包含9个非功能属性。本文从中选出响应时间、可用性, 可靠性这三大属性, 同时随机生成数据集中没有的价格属性, 并以这4个属性评价服务质量。数据集D2是随机生成的, 共收录13 000个Web服务, 包含本文实验所需的QoS属性。
为模拟真实情况下的Web服务组合优化过程, 本文实验设置4种不同子任务数{10, 15, 20, 25}, 并且设置4种不同数量{25, 50, 75, 100}的候选服务集。为保证实验的有效性和正确性, 将5种优化算法在同一数据集上进行实验, 并且每组实验重复40次。
3.2 实验参数设置实验中种群大小均设为30, 最大迭代次数均设为200次, 4个不同的QoS属性权重分别设为:rtm=0.2, ava=0.2, rel=0.3, cos=0.3, 5种群体智能优化算法的参数如表 1所示。
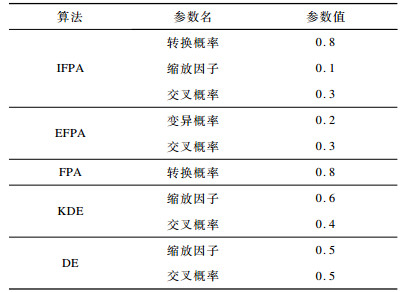
|
下载CSV 表 1 参数设置 Table 1 Parameters setting |
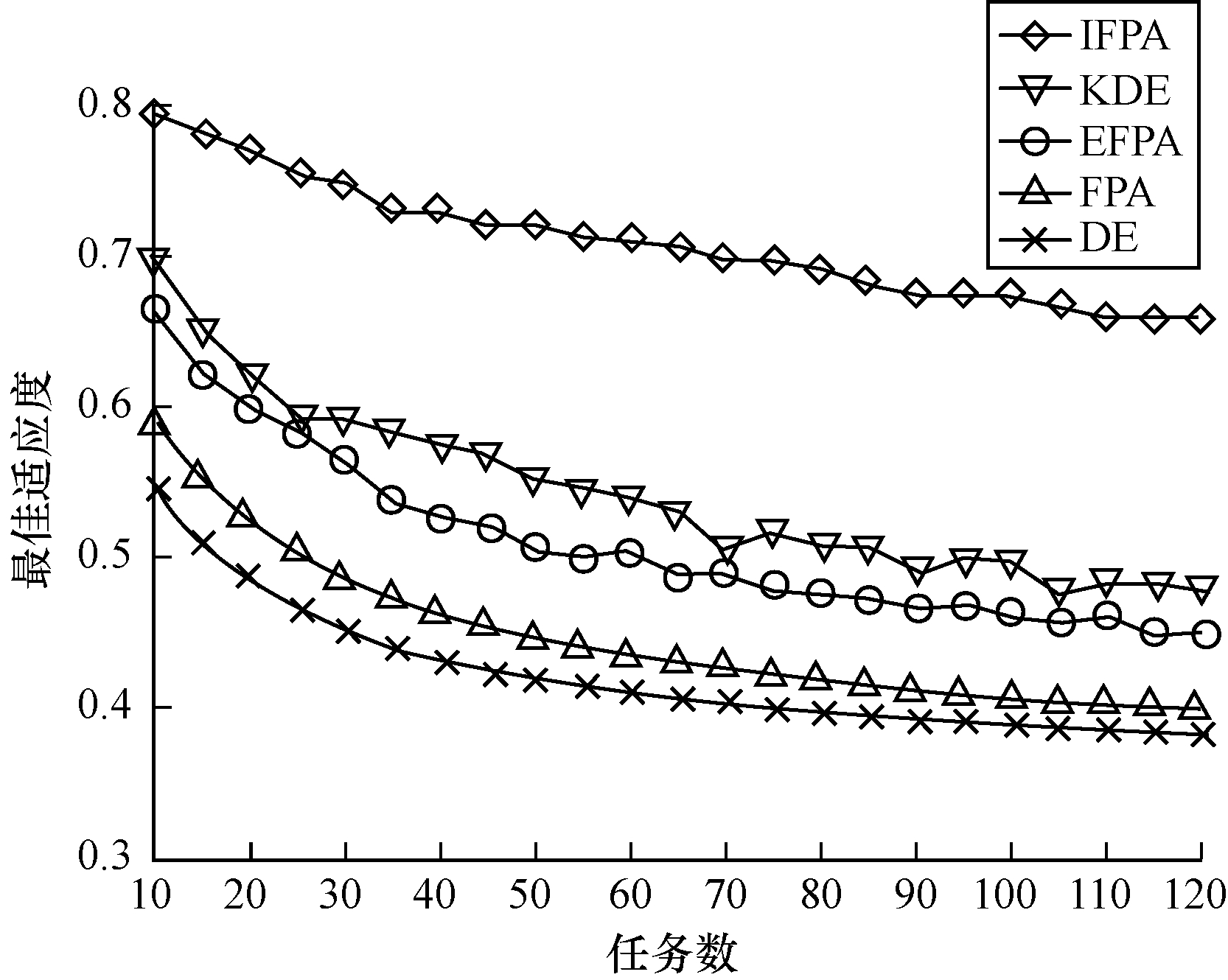
以上文提出的适应度函数评价组合服务的服务质量, 适应度值越大代表服务质量越好, 组合服务的质量越好; 反之, 服务质量越差。为验证IFPA算法在Web服务组合领域的可行性, 在不同任务数与候选服务数的情况下, 比较5种优化算法的寻优性能。此时选取D1数据集, 实验结果如表 2所示。为验证IFPA在大规模服务组合情况下的可行性, 候选服务数均设为100, 此时选取D2数据集, 实验结果如图 1所示。
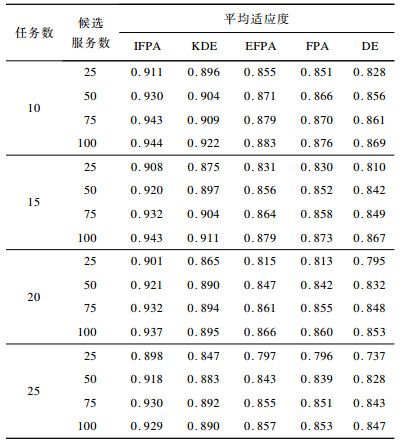
|
下载CSV 表 2 不同任务数和候选服务数下的平均适应度 Table 2 Average fitness under different number of tasks and candidate services |
|
Download:
|
| 图 1 不同任务数下的最佳适应度 Fig. 1 Best fitness under different number of tasks | |
由表 1可以看出, 在不同任务数和不同候选服务数情况下, 相比于其他4种优化算法, IFPA的适应度值均为最高, 即组合服务的质量最好, 验证了IFPA算法的可行性。由图 1可以看出, 在大规模服务组合情况下, IFPA算法也始终优于其他算法。由于IFPA在D1、D2数据集上表现均比其他算法优秀, 因此其不仅可行, 而且寻优性能更好。
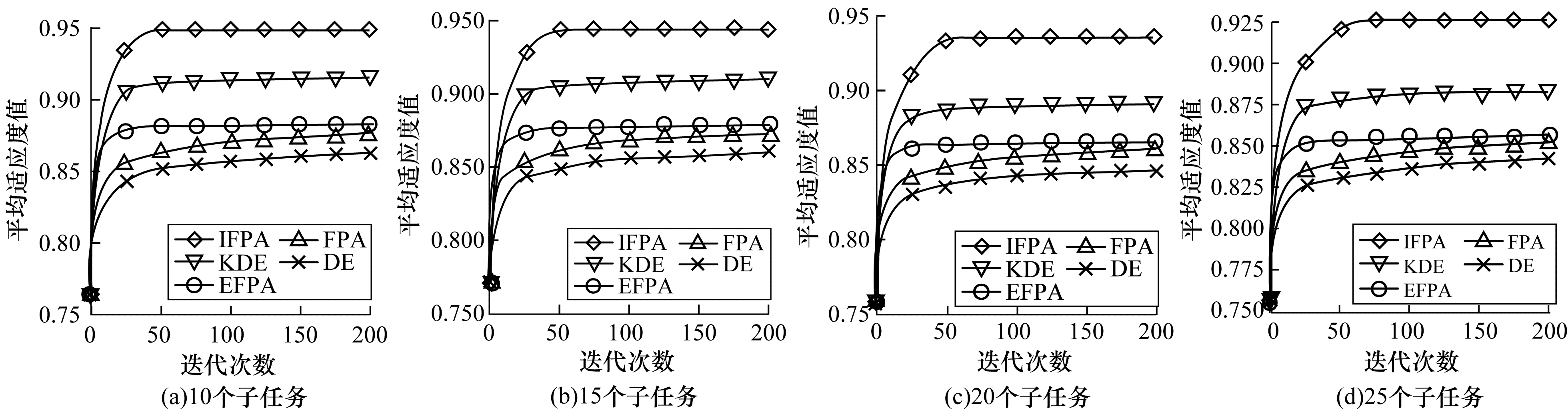
3.4 收敛性分析为分析IFPA的收敛性, 比较不同任务数下5种算法的收敛情况, 即迭代次数和平均适应度之间的关系。在较少的迭代次数下获得较高的平均适应度值, 表示收敛能力较好; 反之, 表示收敛能力较差。实验选取D1数据集, 候选服务数设为100, 结果如图 2所示。
|
Download:
|
| 图 2 迭代次数与适应度之间的关系 Fig. 2 Relationship between the number of iteration and fitness | |
由图 2可以看出, 随着任务数的增加, 5种算法的收敛性能均有所下降。当任务数为10和15时, IFPA算法在迭代到50次时就基本已经收敛; 而当任务数为20和25时, IFPA算法在迭代50次时还未收敛。在4种不同任务数的情况下, IFPA、KDE和EFPA算法的收敛性能优于DE和FPA两种传统优化算法, 同时IFPA算法的平均适应度值都高于另外4种优化算法, 而KDE、EFPA则陷入局部最优解。相比之下, IFPA算法不仅收敛快, 而且寻优性能更好。
4 结束语针对基于QoS感知的Web服务组合优化问题, 本文提出一种改进的花朵授粉算法, 以提高组合服务的服务质量。该算法具有较好的全局搜索能力, 其通过变异、交叉的方式提升种群多样性, 并借助贪心策略提高收敛速度。实验结果验证了该算法在寻优和收敛方面的优越性。本文主要基于静态QoS属性研究Web服务组合优化问题, 但在实际情况下, QoS属性值都是动态变化的, 并且不同属性之间可能存在某种关联关系。因此, 下一步将从动态变化的QoS值以及属性之间的关联这两方面着手, 对本文算法做进一步优化。
| [1] |
TAN Wenan, ZHAO Yao. Web service composition based on chaos genetic algorithm[J]. Computer Integrated Manufacturing Systems, 2018, 24(7): 1822-1829. (in Chinese) 谭文安, 赵尧. 基于混沌遗传算法的Web服务组合[J]. 计算机集成制造系统, 2018, 24(7): 1822-1829. |
| [2] |
WEN Tao, SHENG Guojun, GUO Quan, et al. Web service composition based on modified particle swarm optimization[J]. Chinese Journal of Computers, 2013, 36(5): 1031-1046. (in Chinese) 温涛, 盛国军, 郭权, 等. 基于改进粒子群算法的Web服务组合[J]. 计算机学报, 2013, 36(5): 1031-1046. |
| [3] |
LIU Zhizhong, CHU Dianhui, JIA Zongpu, et al. Two-stage approach for reliable dynamic Web service composition[J]. Knowledge-Based Systems, 2016, 97: 123-143. DOI:10.1016/j.knosys.2016.01.010 |
| [4] |
OUYANG Chao, CHEN Zhibo, SUN Guodong. Improved genetic algorithm for Web service composition QoS optimization[J]. Computer Engineering, 2017, 43(8): 231-235, 242. (in Chinese) 欧阳超, 陈志泊, 孙国栋. Web服务组合QoS优化中的改进遗传算法[J]. 计算机工程, 2017, 43(8): 231-235, 242. |
| [5] |
YILMAZ A E, KARAGOZ P.Improved genetic algorithm based approach for QoS aware Web service composition[C]//Proceedings of 2014 IEEE International Conference on Web Services.Washington D.C., USA: IEEE Press, 2014: 1-5.
|
| [6] |
YE Hengzhou, GUAN Yunhui. QoS-aware Web service composition based on local selection and genetic algorithm[J]. Journal of Chinese Computer Systems, 2016, 37(7): 1389-1392. (in Chinese) 叶恒舟, 关云慧. 基于局部选择和遗传算法的QoS感知的服务组合方法[J]. 小型微型计算机系统, 2016, 37(7): 1389-1392. |
| [7] |
XU X L, RONG H Z, ELLA P, et al. Predatory Search-based Chaos Turbo Particle Swarm Optimization(PS-CTPSO):a new particle swarm optimization algorithm for Web service combination problems[J]. Future Generation Computer Systems, 2018, 89: 375-386. DOI:10.1016/j.future.2018.07.002 |
| [8] |
GAO Honghao, ZHANG Kang, YANG Jianhua, et al. Applying improved particle swarm optimization for dynamic service composition focusing on quality of service evaluations under hybrid networks[J]. International Journal of Distributed Sensor Networks, 2018, 14(2): 1-14. |
| [9] |
POP F C, PALLEZ D, CREMENE M, et al.QoS-based service optimization using differential evolution[C]//Proceedings of Genetic and Evolutionary Computation Conference.New York, USA: ACM Press, 2011: 1891-1898.
|
| [10] |
QI Jin, XU Bin, XUE Yu, et al. Knowledge based differential evolution for cloud computing service composition[J]. Journal of Ambient Intelligence and Humanized Computing, 2017, 9(3): 565-574. |
| [11] |
HUO Ying, ZHUANG Yi, GU Jingjing, et al. Discrete gbest-guided artificial bee colony algorithm for cloud service composition[J]. Applied Intelligence, 2015, 42(4): 661-678. DOI:10.1007/s10489-014-0617-y |
| [12] |
CHANDRA M, NIYOGI R. Web service selection using modified artificial bee colony algorithm[J]. IEEE Access, 2019, 7: 88673-88684. DOI:10.1109/ACCESS.2019.2926155 |
| [13] |
ZHANG Wenyu, YANG Yushu, ZHANG Shuai, et al. Correla-tion-aware manufacturing service composition model using an extended flower pollination algorithm[J]. International Journal of Production Research, 2018, 56(14): 4676-4691. DOI:10.1080/00207543.2017.1402137 |
| [14] |
ZHAO Xinchao, SONG Boqian, HUANG Panyu, et al. An improved discrete immune optimization algorithm based on PSO for QoS-driven Web service composition[J]. Applied Soft Computing Journal, 2012, 12(8): 2208-2216. DOI:10.1016/j.asoc.2012.03.040 |
| [15] |
HAYYOLALAM V, KAZEM A A P. A systematic literature review on QoS-aware service composition and selection in cloud environment[J]. Journal of Network & Computer Applications, 2018, 110: 52-74. |
| [16] |
YANG X S, KARAMANOGLU M, HE X S. Flower pollination algorithm:a novel approach for multi-objective optimization[J]. Engineering Optimization, 2014, 46(9): 1222-1237. DOI:10.1080/0305215X.2013.832237 |
| [17] |
THANGAVELU S, VELAYUTHAM C S.An investigation on mixing heterogeneous differential evolution variants in a distributed framework[M].[S.l.]: Inderscience Publishers, 2015.
|
| [18] |
ZHOU Jiajun, YAO Xifan. Multi-population parallel self-adaptive differential artificial bee colony algorithm with application in large-scale service composition for cloud manufacturing[J]. Applied Soft Computing, 2017, 56: 379-397. DOI:10.1016/j.asoc.2017.03.017 |
| [19] |
XIAO Xiaoli, WU Yao, ZHOU Xiling, et al. Two-stage text feature selection algorithm based on differential evolution[J]. Computer Engineering, 2019, 45(2): 303-309, 314. (in Chinese) 肖晓丽, 吴瑶, 周锡玲, 等. 基于差分进化的两阶段文本特征选择算法[J]. 计算机工程, 2019, 45(2): 303-309, 314. |
| [20] |
ZENG L, BENATALLAH B, DUMAS M, et al.Quality driven Web services composition[C]//Proceedings of the 12th International Conference on World Wide Web.New York, USA: ACM Press, 2003: 411-421.
|
| [21] |
ZENG L, BENATALLAH B, NGU A H H, et al. Qos-aware middleware for Web services composition[J]. IEEE Transactions on Software Engineering, 2004, 30(5): 311-327. DOI:10.1109/TSE.2004.11 |
 2020, Vol. 46
2020, Vol. 46
