视觉里程计[1-2]是移动机器人自主建图与定位的关键技术, 其在要求传感器体积小、重量轻、功耗小以及价格低的场合具有较大优势。应用单目视觉里程计[3]时存在的一个重要问题是相机在快速或剧烈运动时, 里程计算法的鲁棒性较低[4-5], 原因是相机快速运动时难以建立可靠的特征匹配关系, 此外地图扩展更新模块存在一定的延迟, 没有及时生成地图点, 导致在相机快速或剧烈运动时没有足够多的地图点用于跟踪[6]。
对于单目视觉里程计算法, 特征匹配需要综合考虑算法的实时性和鲁棒性。MonoSLAM算法[7]先采用卡尔曼滤波[8]预测特征点在下一帧的位置, 然后进行主动搜索加速特征匹配。并行跟踪和建图(PTAM)算法[9]和ORB-SLAM算法[10]利用相机匀速运动模型估计当前帧位姿, 再将3D地图点投影到当前帧中, 从而缩小搜索范围以加速匹配。ENGLE等人[11]提出的大尺度直接单目SLAM算法(LSD-SLAM)假设相机运动非常缓慢, 直接用上一帧的位姿初始化当前帧位姿, 然后进行图像对齐。在相机运动较为剧烈时, 匀速[9-10]或者静止[11]等运动模型都存在较大误差, 滤波方法[6]由于误差累积也会导致特征匹配失败, 因此, 需要提高系统的鲁棒性。文献[12]通过增加线特征来提高特征匹配的成功率, 文献[13]引入机器人轮子编码器信息从而提高特征匹配的鲁棒性。
地图的扩展速度也是影响算法实时性和鲁棒性的一个重要因素。目前, 较多性能良好的视觉SLAM算法, 如ORB-SLAM、半直接视觉里程计(SVO)[14]、直接稀疏里程计(DSO)[15]等, 为了提高算法的实时性和精度, 将地图的扩展更新与位姿跟踪分离, 导致地图扩展更新有数帧甚至数十帧的延迟。然而, 在相机快速或剧烈运动的情况下, 对视角较小的单目视觉而言, 地图扩展更新延迟意味着没有足够多的地图点用于跟踪, 从而降低了系统的鲁棒性。
本文针对单目视觉里程计在相机快速或剧烈运动时鲁棒性较低的问题, 提出一种基于树结构特征匹配和实时地图更新的单目视觉里程计算法。设计基于树结构和RANASC算法[16]的特征匹配算法, 采用无运动假设的树结构进行特征匹配, 以保证算法的实时性和特征匹配的鲁棒性, 通过结合汉明距离的RANASC算法剔除误匹配。建立地图实时扩展更新框架, 在跟踪线程, 基于当前帧与关键帧的匹配关系实时扩展更新地图, 并针对视差大小采取不同的深度估计策略来生成不同类型的地图点, 在局部地图优化线程中进行局部地图的优化。建立基于视差的权重矩阵估计模型, 根据视差大小估计优化函数中残差项的权重矩阵, 使精度高的地图点在优化函数中占主导地位。
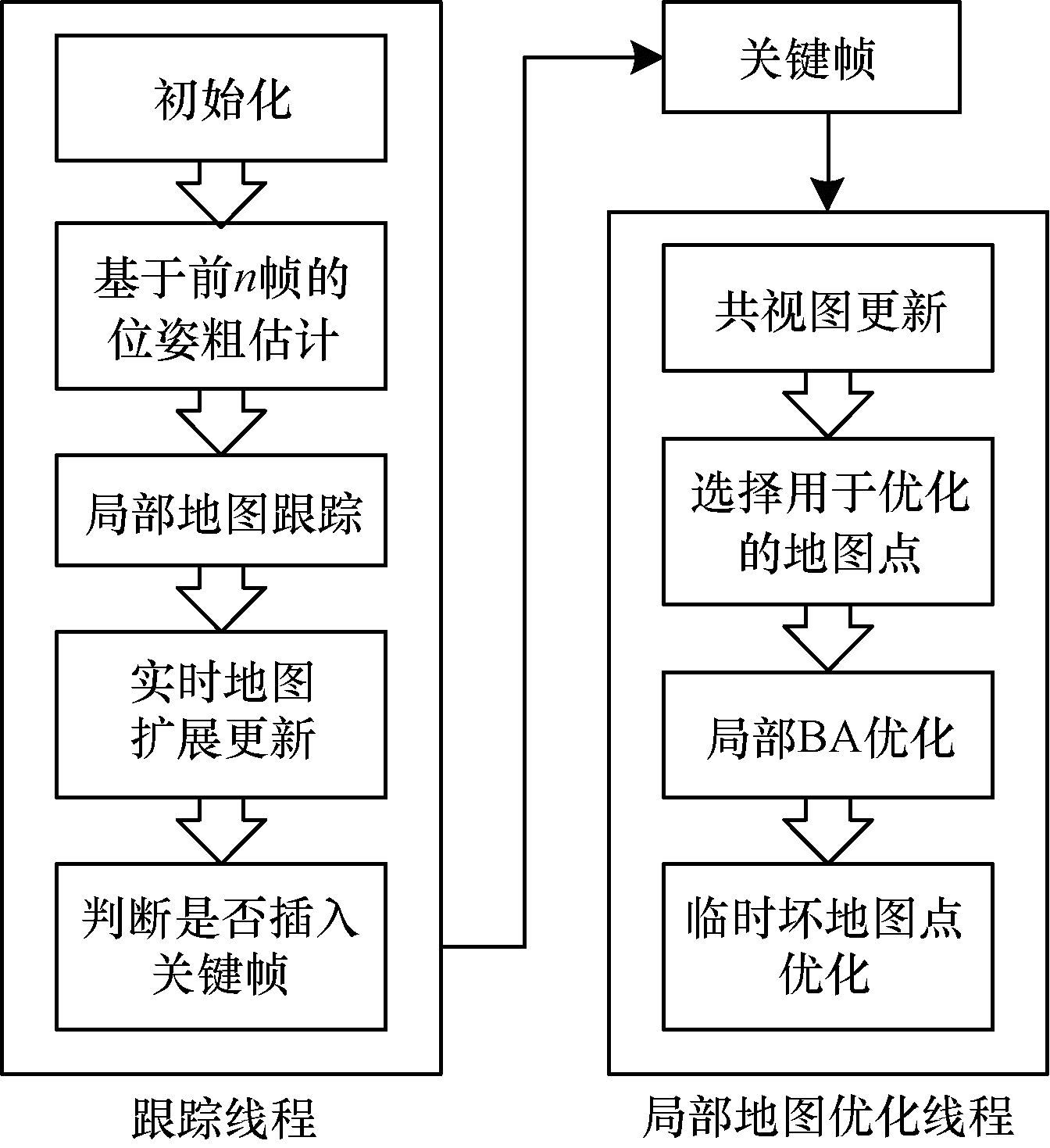
1 单目视觉里程计算法框架如图 1所示, 单目视觉里程计算法包括跟踪与局部地图优化2个线程。在跟踪线程, 首先根据特征树建立当前帧与前n帧的特征匹配关系, 用于求解当前帧的粗位姿, 然后通过跟踪局部地图来优化粗位姿, 最后基于当前帧与关键帧之间的匹配关系, 根据视差大小采用2种策略生成不同类型的3D地图点, 完成地图的实时扩展更新。在局部地图优化线程, 首先将关键帧位姿与高精度的地图点联合优化, 提高地图精度, 然后将优化后的高精度位姿作为约束来优化临时坏地图点从而完成地图优化。将跟踪与局部地图优化相分离, 有利于提高地图优化的精度和效率。
|
Download:
|
| 图 1 单目视觉里程计算法框架 Fig. 1 Monocular visual odometry algorithm framework | |
基于运动假设的运动模型无法适用于剧烈运动的情况, 本文基于特征树建立特征匹配关系, 并用RANSAC算法来剔除误匹配,具体过程如下:
1) 特征树构建
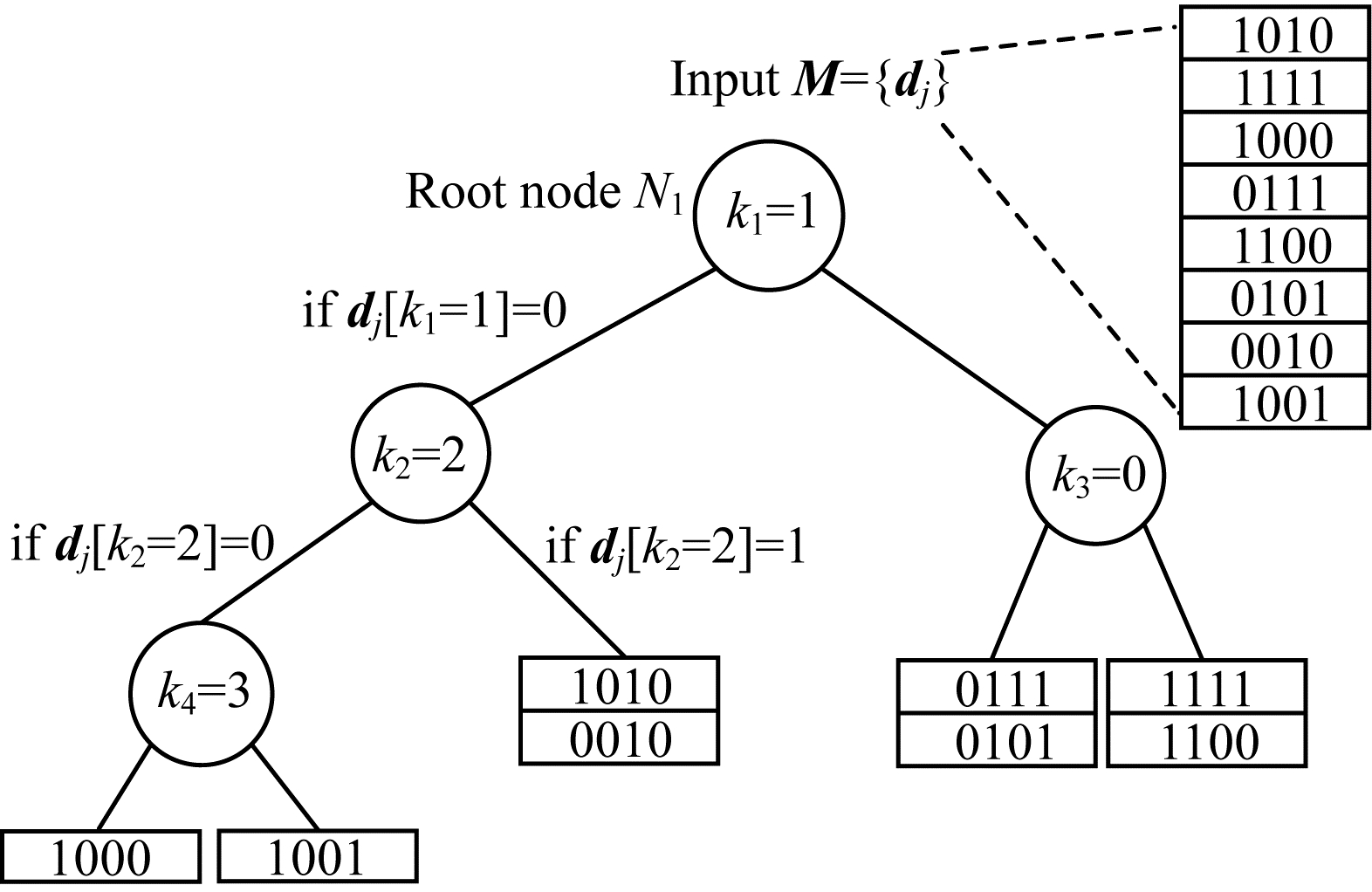
如图 2所示, 将每一帧图像的描述子{dj}都构建为一棵类二叉树的特征树。特征树的非叶节点Ni储存描述子的位索引号ki, ki∈[0, 1, …, dim(d)-1], dim(d)指描述子的维数, 示例图像中的描述子维数为4。根据输入的描述子在位索引号上的值将其分配到左、右节点中。最终, 特征树的每个叶节点Li都储存了描述子集合{dj}的一个子集合{di, j}。
|
Download:
|
| 图 2 特征树结构 Fig. 2 Feature tree structure | |
位索引号通过如下方式确定:
(1) 任意指定。该方法操作简单, 但是不能保证建立的二叉树是近似平衡的, 会提高搜索的代价。
(2) 统计输入描述子中ki位为1所占的比例。当ki位为1所占的比例ratio(ki)足够接近0.5时, ki即为位索引号, 该方法可以保证特征树近似平衡。ratio(ki)的计算方法如下:
| $ {\mathop{\rm ratio}\nolimits} \left( {{k_i}} \right) = \frac{1}{{\dim (\mathit{\boldsymbol{d}})}}\sum\limits_{j = 0}^{\dim (\mathit{\boldsymbol{d}})} {{\mathit{\boldsymbol{d}}_j}} \left[ {{k_i}} \right] $ | (1) |
2) 基于特征树的特征匹配
将N个描述子构建成一棵深度为h的平衡树, 则每个叶节点描述子个数为
描述子之间的汉明距离表征了匹配的可靠性, 正确匹配点对之间的汉明距离应小于阈值ρ。描述子ds在一棵深度为h的特征树中能找到匹配描述子dm的概率为:
| $ {P = \prod\limits_i^h p \left( {{\mathit{\boldsymbol{d}}_s}\left[ {{k_i}} \right] = {\mathit{\boldsymbol{d}}_m}\left[ {{k_i}} \right]} \right)} $ | (2) |
| $ {P \ge \prod\limits_i^h {\frac{{\dim (\mathit{\boldsymbol{d}}) - \rho }}{{\dim (\mathit{\boldsymbol{d}})}}} } $ | (3) |
结合后文中的跟踪前n帧策略, 对于能被前k帧观测到的特征点, 最终能找到对应匹配描述子的概率为:
| $ {P^\prime }(k) \ge 1 - {(1 - P)^{\hat k}} $ | (4) |
结合工程应用可知, 一般匹配点的汉明距离阈值ρ小于最小汉明距离的2倍, 最大不超过25, 这里取ρ=20, 深度h=4, 则不同帧数下能找到特征匹配的概率如表 1所示。

|
下载CSV 表 1 特征匹配的概率 Table 1 Probability of feature matching |
3) 基于RANSAC算法的误匹配剔除
本文结合汉明距离提出基于RANSAC算法的误匹配剔除算法。为了减少迭代次数并提高RANSAC算法的速度, 迭代过程中的随机数据只在汉明距离较小的点对中选取。根据随机数据, 采用经典的八点法来计算基础矩阵F, 并依次判断所有特征点对(x′j, xj)是否满足||x′jFxj||≤th, th为内点阈值, 直至找到足够大的内点比例或达到最大迭代次数。
2.1.2 基于前n帧的位姿粗估计在相机快速平移或旋转时, 当前帧与前一帧之间或当前帧与参考关键帧之间的视角重叠较小, 无法得到足够数量的特征匹配来估计稳定的相机位姿, 从而导致跟踪失败。
针对上述问题, 本文提出跟踪前n帧的策略来增加视角的重叠并引入更多的信息量。假定当前帧的帧号为k, 则这n帧中至少包含k-1帧、参考关键帧以及最近的关键帧。若当前帧跟踪到的3D地图点数量小于阈值γ, 则会依次跟踪k-3帧、k-5帧, 直至匹配的特征点数目大于γ或超出最大的n值。前n帧中包含参考关键帧、最近关键帧的原因是:1)关键帧可以为后面的实时地图更新模块提供具有一定视差的2D-2D的特征匹配点; 2)参考关键帧、最近关键帧与当前帧最有可能具有大量的共视点, 从而保证了当前帧能跟踪到足够的3D地图点。
结合上文中提到的特征匹配算法, 可以得到足够的3D-2D、2D-2D特征匹配关系。本文仅使用3D-2D匹配关系, 通过最小化重投影误差的平方和来估计相机的粗位姿Tk, w, 代价函数为:
| $ {{\mathit{\boldsymbol{T}}_{k,w}} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{{T_{k,w}}} \frac{1}{2}\sum\limits_i {{{\left\| {\mathit{\boldsymbol{e}}_i^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^{ - 1}{\mathit{\boldsymbol{e}}_i}} \right\|}^2}} } $ | (5) |
| $ {{\mathit{\boldsymbol{e}}_i} = {\mathit{\boldsymbol{x}}_i} - {\rm{ \mathsf{ π} }}\left( {\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{T}}_{k,w}}{\mathit{\boldsymbol{P}}_i}} \right)} $ | (6) |
| $ {\mathit{\boldsymbol{\pi }}\left( {{{\left[ {{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}, \cdots ,{\mathit{\boldsymbol{x}}_n}} \right]}^{\rm{T}}}} \right) = {{\left[ {\frac{{{\mathit{\boldsymbol{x}}_1}}}{{{\mathit{\boldsymbol{x}}_n}}},\frac{{{\mathit{\boldsymbol{x}}_2}}}{{{\mathit{\boldsymbol{x}}_n}}}, \cdots ,\frac{{{\mathit{\boldsymbol{x}}_{n - 1}}}}{{{\mathit{\boldsymbol{x}}_n}}}} \right]}^{\rm{T}}}} $ | (7) |
其中, Σ-1为权重矩阵, 由后文中的估计方法给定, Pi为当前帧观测到的地图点, xi为匹配特征点的像素坐标, K为相机的内参矩阵。
2.2 局部地图跟踪局部地图是根据两级共视关系而确定的, 局部地图中关键帧能观测到的地图点称为局部地图点。在建立局部地图点与当前帧之间的3D-2D匹配关系后, 通过最小化重投影误差来优化粗位姿, 代价函数如下:
| $ {\mathit{\boldsymbol{T}}_{k,w}} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{{\mathit{\boldsymbol{T}}_{k,w}}} \sum\limits_i \rho \left( {\left\| {{\mathit{\boldsymbol{x}}_i} - \pi \left( {\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{T}}_{k,w}}{\mathit{\boldsymbol{P}}_i}} \right)} \right\|_{{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}^{ - 1}}}^2} \right) $ | (8) |
其中, xi与Pi分别为对应的像素点坐标和局部地图点坐标, ρ(e)为鲁棒核函数, 本文采用Huber核函数:
| $ \rho (\mathit{\boldsymbol{e}}) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}{\mathit{\boldsymbol{e}}^2},|\mathit{\boldsymbol{e}}| \le \delta }\\ {\delta \left( {|\mathit{\boldsymbol{e}}| - \frac{1}{2}\delta } \right),{\rm{ 其他}}} \end{array}} \right. $ | (9) |
由式(9)可以看出, 当误差e大于阈值δ时, 函数由二次函数变成了一次函数, 相当于限制了迭代求解中梯度的最大值, 减弱了错误特征匹配的影响, 提高了位姿估计的精度。
2.3 地图扩展与关键帧插入实时地图扩展更新能保证当前帧跟踪到足够多的地图点, 使算法对快速运动具有较好的鲁棒性。
2.3.1 实时地图扩展更新特征匹配阶段已经得到了当前帧与参考关键帧、最近关键帧之间的2D-2D特征匹配关系, 此时只需准确估计3D点的深度值。视差大小对三角化[17]的精度影响较大, 为保证地图点位置估计的精度, 针对不同视差采取不同的深度估计策略。对于匹配点对xk(位于关键帧)和xi(位于当前帧), 视差大小通过光心与两点连线方向上的单位向量夹角α(k, i)=cos-1(rkTri)表示, 其中,
对于视差α(k, i)大于阈值βα的点对, 直接通过三角测量法进行深度估计。如果α(k, i)小于βα且大于γα, 则先将xk临近点的平均深度作为初始深度值dinit, 然后通过最小化重投影误差来优化深度值。对于视差过小的匹配点对, 如无穷远处的点, 则不做处理, 以避免相机保持静止时进行地图扩展[18]。求xk和xi对应的地图点P时需要解如下的优化问题:
| $ \mathit{\boldsymbol{P}} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_\mathit{\boldsymbol{P}} \frac{1}{2}\left( {\left\| {{\mathit{\boldsymbol{e}}_k}} \right\|_2^2 + \left\| {{\mathit{\boldsymbol{e}}_i}} \right\|_2^2} \right) $ | (10) |
其中, 重投影误差为e=x-π(KTk, wP), 地图点初始值为Pinit=Tw, kdinitK-1[xkT x]T。
2.3.2 基于视差的权重矩阵估计本文将地图点分成3类, 并结合视差的大小和地图点类型计算地图点对应残差项的权重矩阵。跟踪线程中通过三角化得到的地图点视差较大、位置精度较高, 将其记为临时好地图点, 可直接用于跟踪; 通过优化得到的地图点初始深度值较差, 且仅依靠两帧的观测来优化深度值, 位置精度较低, 将其标记为临时坏地图点。将经过局部地图优化线程多视角约束优化后仍被保留下来的临时好地图点标记为永久地图点, 并对其分配最大的权重矩阵。
权重矩阵估计步骤具体如下:
1) 判断地图点的类型。对于永久地图点, 则权重矩阵为单位矩阵; 对于临时地图点, 根据后续步骤计算权重矩阵。
2) 统计优化方程中所有临时地图点生成时的最大视差αmax。
3) 对于地图点Pi, 计算
| $ \mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_i^{ - 1} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\sigma }}_i^{ - 1}}&0\\ 0&{\mathit{\boldsymbol{\sigma }}_i^{ - 1}} \end{array}} \right] $ | (11) |
在优化方程中添加上述权重矩阵, 可以使精度高的地图点对应的残差项在优化过程中占主导作用, 从而提高位姿的估计精度。
2.3.3 关键帧选择及时生成关键帧有利于提高位姿和地图点的估计精度。考虑到局部地图优化线程无需进行地图扩展, 计算代价较低, 本文采取较为简单的关键帧插入策略。插入一个新的关键帧至少需要满足以下条件中的一个条件:
1) 在当前帧跟踪到的地图点中, 临时地图点比例超过30%。
2) 局部地图优化线程是空闲的, 且距离上一个关键帧已经超过了1 s。
3) 当前帧跟踪到的地图点少于50个。
4) 当前帧跟踪参考关键帧的永久地图点所占比例少于80%。
3 局部地图优化线程局部地图优化线程主要实现关键帧位姿和地图点的优化以及临时地图点的处理。
3.1 共视图更新和地图点选择将局部地图的3D点投影到当前关键帧中建立更多匹配, 同时也将当前关键帧的3D地图点投影到局部地图的关键帧中, 完成共视图的更新。局部地图点包含永久地图点、临时好地图点和临时坏地图点3类点。所有的永久地图点都用于位姿优化, 所有的临时坏地图点都不用于位姿优化。对于临时好地图点, 先计算地图点在关键帧中的平均投影误差δe, 丢弃投影误差大于1.2δe的匹配关系, 然后将所有临时好地图点用于位姿优化。
3.2 局部BA优化与临时坏地图点优化将局部地图中的当前关键帧、一级共视关键帧、永久地图点和临时好地图点一起联合优化, 而二级共视关键帧在优化过程中会被固定, 用于为地图点提供约束。在优化结束后, 所有参与优化的临时好地图点精度进一步提高, 因此, 将其标记为永久地图点。
临时坏地图点之所以不直接用于BA优化, 是考虑到其不准确的位置会导致优化结果错误。本文采用固定优化后的位姿以及多视角的约束关系来优化临时坏地图点, 这样既不降低位姿的精度, 同时也可以提高临时坏地图点的精度。将优化后的临时坏地图点标记为临时好地图点用于跟踪。每一个临时坏地图点Pi都通过最小化重投影来单独优化, 由于地图点之间相互独立, 可以通过并行计算来加速。优化方程为:
| $ {\mathit{\boldsymbol{P}}_i} = \mathop {{\mathop{\rm argmin}\nolimits} }\limits_{{\mathit{\boldsymbol{P}}_i}} \frac{1}{2}\sum\limits_{{\mathit{\boldsymbol{T}}_{j,w}} \in {\mathit{\boldsymbol{T}}_{{\mathit{\boldsymbol{P}}_i}}}} {\left\| {{\mathit{\boldsymbol{x}}_{j,i}} - {{ { π} }}\left( {\mathit{\boldsymbol{K}}{\mathit{\boldsymbol{T}}_{j,w}}{\mathit{\boldsymbol{P}}_i}} \right)} \right\|_2^2} $ | (12) |
其中, TPi为所有能观测到地图点Pi的关键帧集合, xj, i为地图点Pi在关键帧j中的观测值。
4 实验结果与分析在本文实验中, CPU为Inter i5-7200U, 主频为2.5 Hz, 内存为8 GB, 无GPU加速, 操作系统为Ubuntu16.04。采用公开的KITTI数据集[19](室外)和EuRoC数据集[20](室内)进行实验。
4.1 特征匹配实验为了验证基于树结构和RANASC的特征匹配算法的高效性和精确性, 将本文算法与OpenCV自带的暴力匹配算法进行对比。用于特征匹配实验的图像分别来自EuRoC的V1_01_easy序列和KITTI-02序列, 每张图片上提取的ORB特征点数量均为2 000, 实验结果如图 3、图 4、表 2、表 3所示, 其中, “×”表示包含大量错误匹配, 无法统计匹配比例。

|
Download:
|
| 图 3 EuRoC数据集的匹配结果 Fig. 3 Matching results of EuRoC dataset | |

|
Download:
|
| 图 4 KITTI数据集的匹配结果 Fig. 4 Matching results of KITTI dataset | |
|
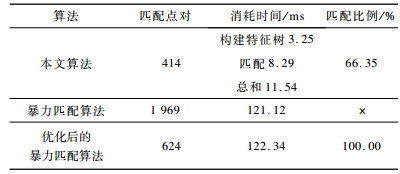
下载CSV 表 2 EuRoC数据集特征匹配结果对比 Table 2 Comparison of feature matching results of EuRoC dataset |
|
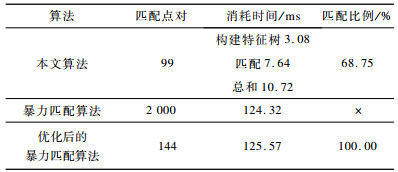
下载CSV 表 3 KITTI数据集特征匹配结果对比 Table 3 Comparison of feature matching results of KITTI dataset |
在图 3、图 4中, 左上角表示提取ORB特征点的原始图像, 右上角表示使用OpenCV自带的暴力匹配算法匹配的结果, 左下角表示将初始暴力匹配的结果通过严格的距离阈值和角度阈值剔除误匹配后的优化结果(可视为匹配的真值), 右下角表示本文特征匹配算法的结果。从图 3、图 4可以看出, 初始的暴力匹配虽然能为每个特征点找到匹配点, 但是存在大量的误匹配, 本文特征匹配算法和优化后的暴力匹配算法虽然丢失了一些匹配, 但是都取得了较高的匹配精度。
从表 2、表 3可以看出, 特征树构建约需要3 ms, 具有很高的效率。而基于树结构和RANASC算法的特征匹配算法相对于优化后的暴力匹配算法, 虽然会丢失部分正确的匹配, 但是计算速度提高了一个数量级。综上, 本文特征匹配算法具有很高的精度和效率。对于丢失部分正确匹配的问题, 本文跟踪前n帧的策略可以在一定程度上提高当前帧特征匹配的比例。
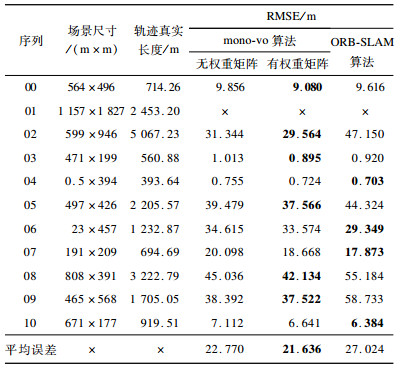
4.2 KITTI数据集室外大尺度实验在本次实验中将本文所提单目视觉里程计算法称为mono-vo算法。KITTI数据集包含从00号到10号的基准数据, 该数据集是通过快速运动车辆上的摄像头采集到的大尺度真实环境。ORB-SLAM是目前最优的纯视觉SLAM算法之一, 本文使用不包含闭环线程的ORB-SLAM算法与mono-vo算法进行对比, 使用evo工具评测算法效果, 用绝对轨迹的均方根误差(RMSE)作为评价指标, 实验结果如表 4所示, 最优结果加粗表示。
|
下载CSV 表 4 KITTI数据集室外大尺度实验结果 Table 4 Outdoor large scale experiment results of KITTI dataset |
从表 4可以看出, 除序列01外, mono-vo与ORB-SLAM均可成功测试其他10个序列。其中, 在平缓的直线运动中, mono-vo与ORB-SLAM具有相近的精度, 而在具有较大旋转的数据集上, mono-vo取得了更好的定位精度, 验证了该算法在相机视角变换较快时具有更好的鲁棒性。在10个序列的整体效果中, mono-vo具有更高的精度, 此外, 带权重矩阵的mono-vo算法比无权重矩阵的mono-vo算法的定位精度更高, 验证了基于视差的权重矩阵估计方法的有效性。
结合序列01、02、03和04的具体环境及轨迹来分析表 4结果以及算法的实时性表现。从图 5可以看出, 序列01的环境是高速公路, 道路两边非常空旷, 能观测到的特征点绝大部分都是很远的点, 太远的观测点导致生成地图点时视差过小, 无法正确估计地图点深度, 不适用于纯单目视觉算法。

|
Download:
|
| 图 5 序列01环境 Fig. 5 Environment of sequence 01 | |
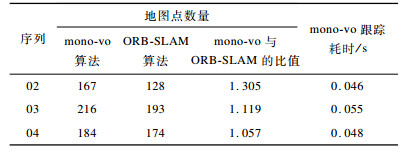
在序列02、03和04的数据集实验中, 每帧提取2 000个ORB特征点, 统计当前帧能跟踪到的地图点数量和单帧跟踪耗时, 结果如表 5所示。
|
下载CSV 表 5 当前帧能跟踪到的地图点数量和单帧跟踪耗时 Table 5 The number of map points that can be tracked in the current frame and the tracking time of a single frame |
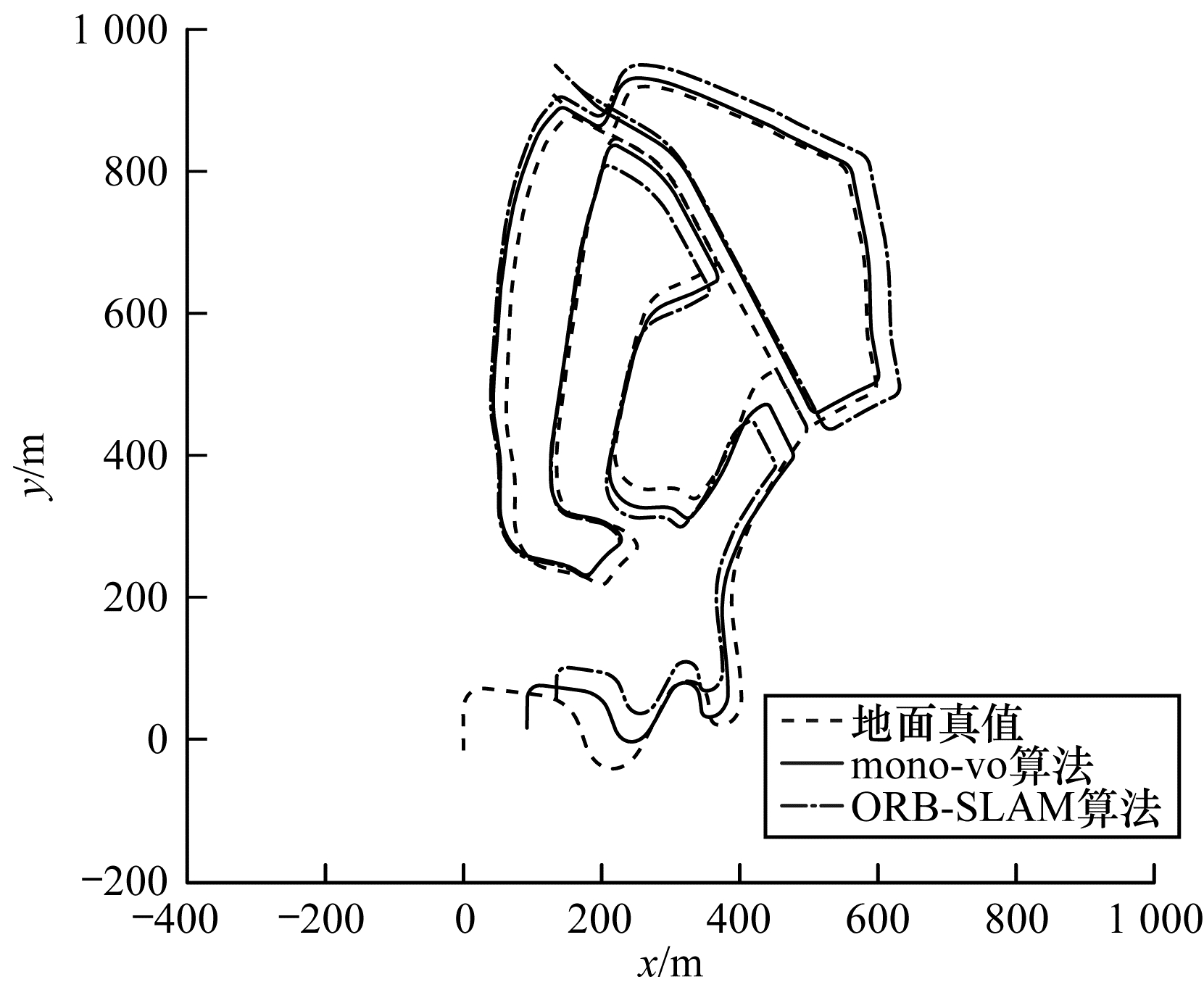
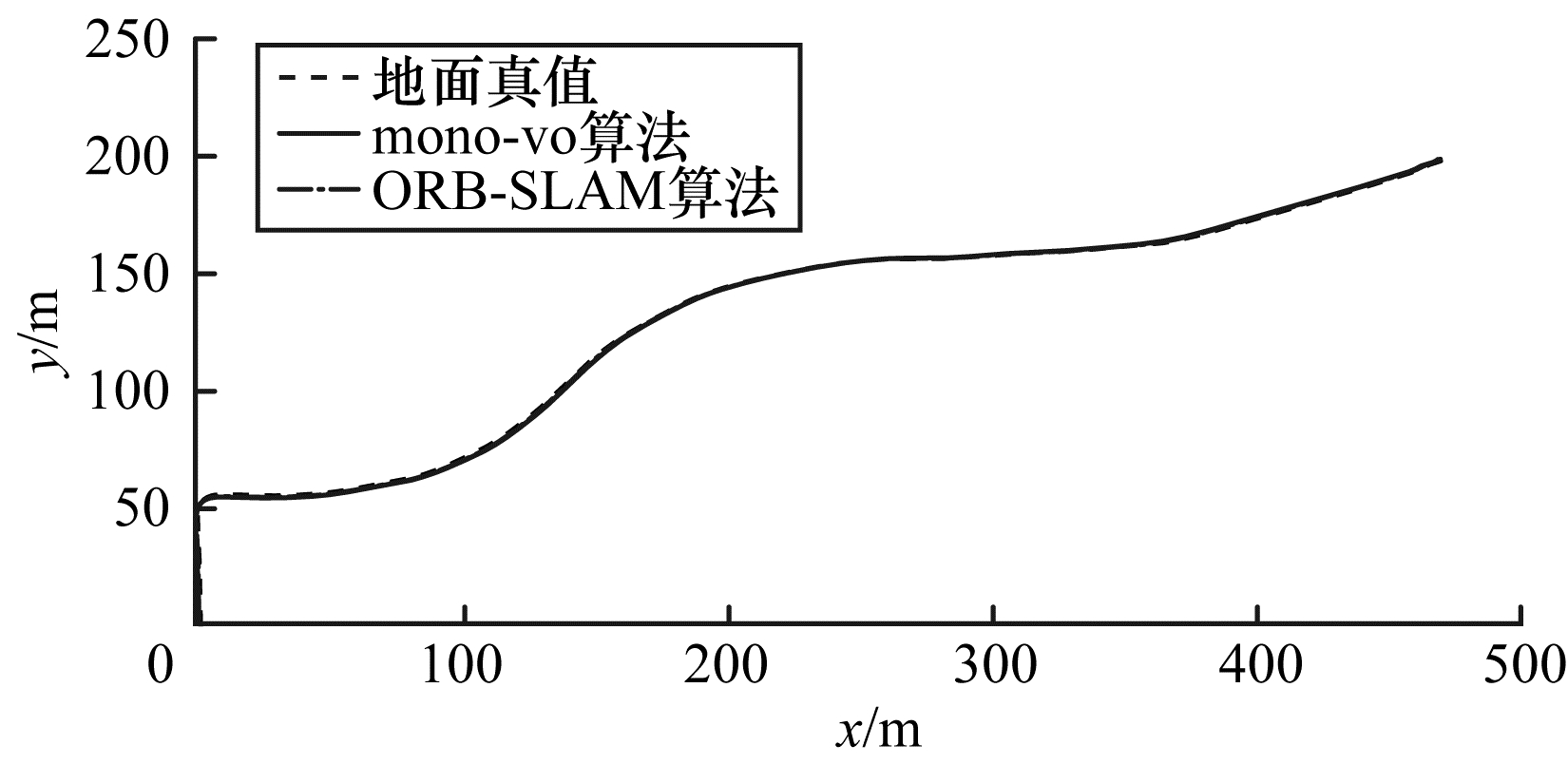
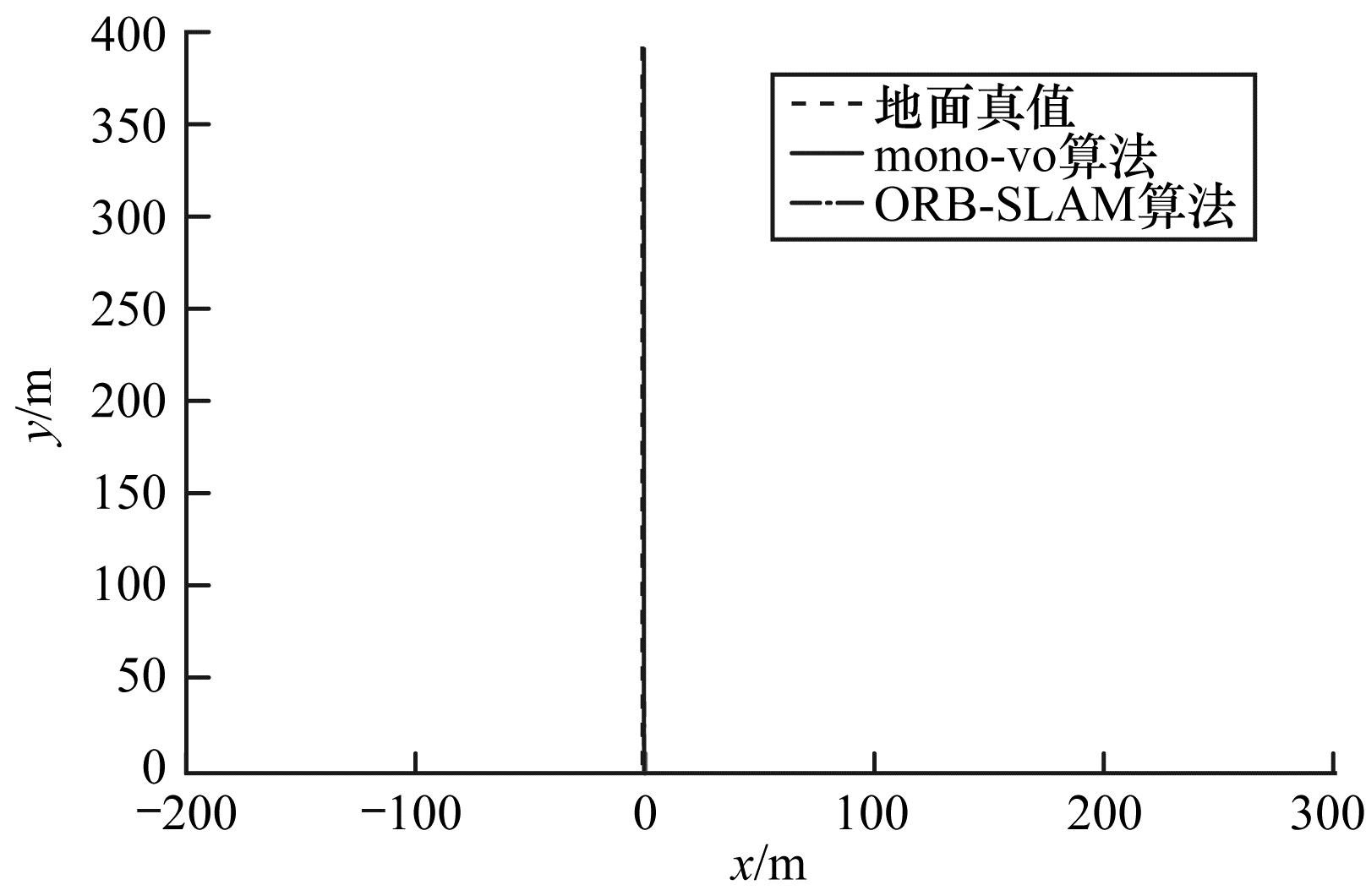
从表 5、图 6、图 7可以看出, 序列02、03包含大量的曲线运动, 且具有较大的旋转角度, mono-vo算法中跟踪前n帧的策略可以增加视角的重叠, 引入更多的信息, 同时基于树结构的特征匹配算法和实时地图更新策略可以保证当前帧跟踪到更多的地图点, 从而提高了位姿估计的精度。从表 5、图 8可以看出, 在以直线运动为主的数据集中, mono-vo算法取得了与ORB-SLAM算法相近的精度, 这是由于在直线运动中, 帧间的视角重叠较大, 跟踪前n帧的策略并不会引入太多的信息。由单帧消耗的平均时间可知, mono-vo算法的跟踪频率在18 Hz~22 Hz范围内, 其具有很好的实时性。
|
Download:
|
| 图 6 序列02跟踪结果 Fig. 6 Tracking results of sequence 02 | |
|
Download:
|
| 图 7 序列03跟踪结果 Fig. 7 Tracking results of sequence 03 | |
|
Download:
|
| 图 8 序列04跟踪结果 Fig. 8 Tracking results of sequence 04 | |
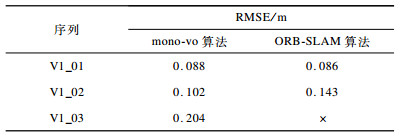
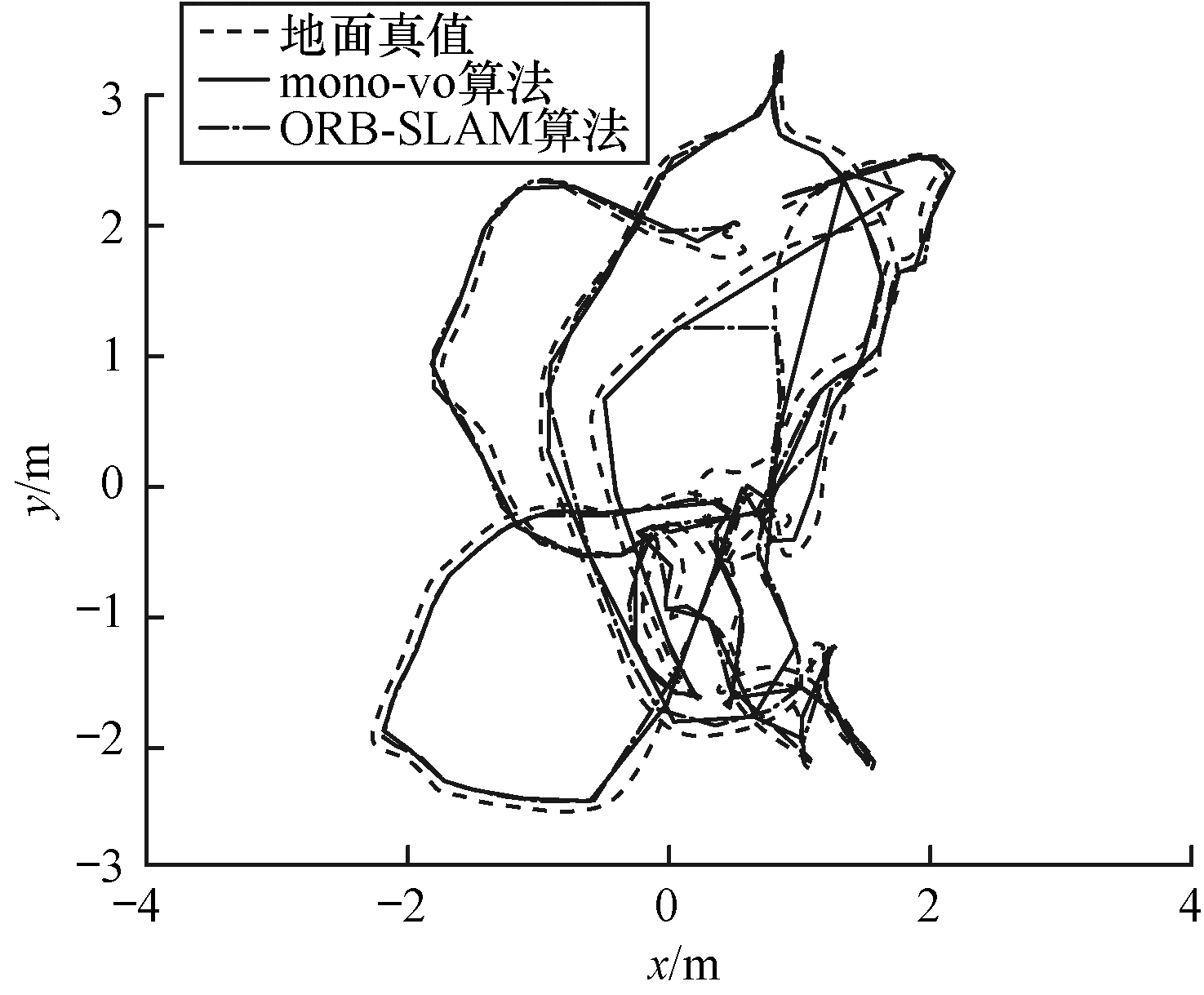
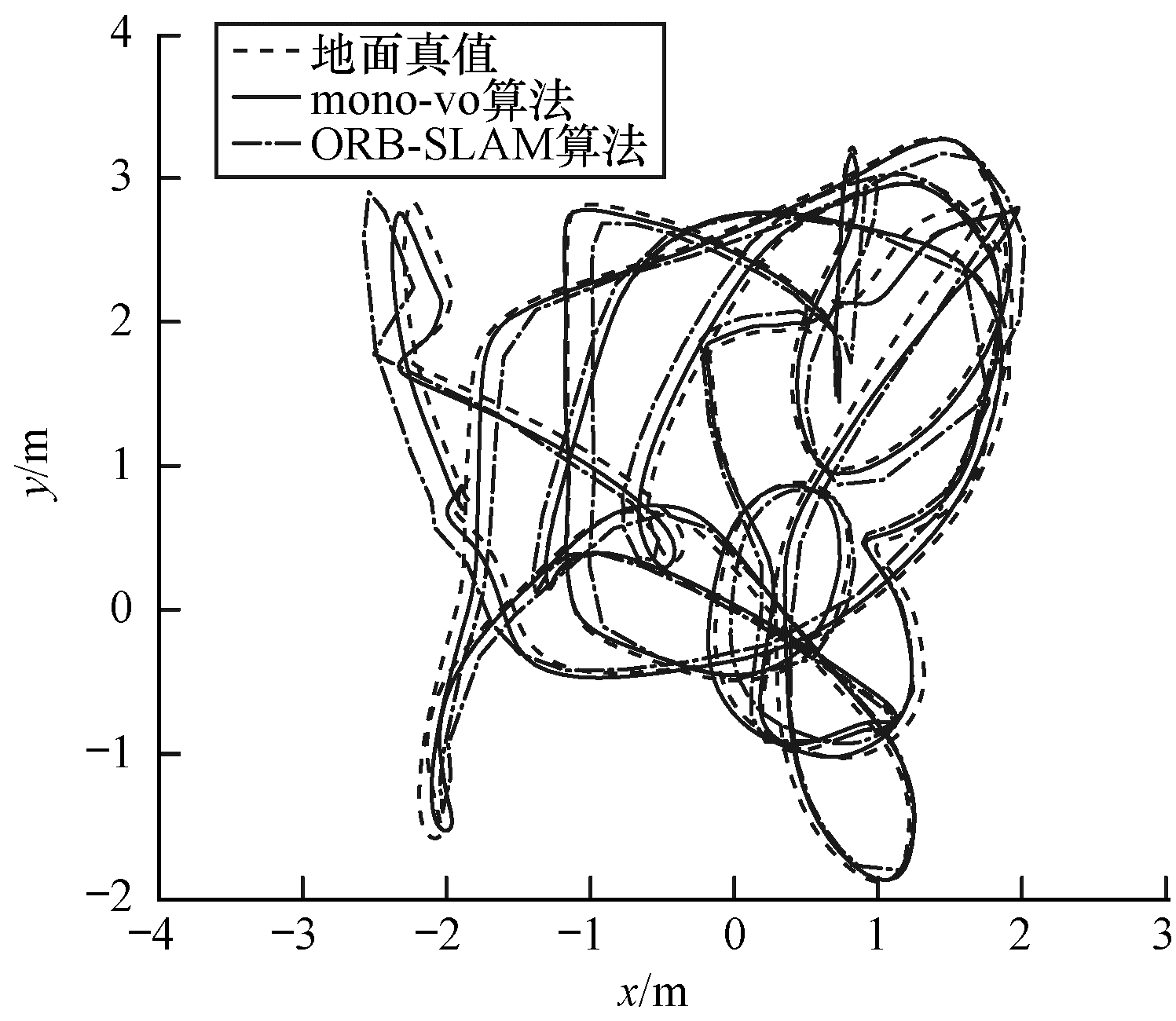
EuRoC数据集是在室内小尺度人工环境下通过无人机采集的图像序列。本文实验采用V1_01、V1_02、V1_03 3个序列, 难度依次增加, V1_03序列包含大量的剧烈旋转与平移, 且存在跳帧情况。实验结果如表 6、图 9~图 11所示。从中可以看出, 在运动较平缓时, mono-vo与ORB-SLAM都有很好的定位精度, 但在剧烈运动和跳帧场景下, ORB-SLAM算法无法跟踪到足够的地图点, 而mono-vo算法通过基于树的特征匹配算法和实时地图扩展更新策略, 依然可以顺利地测试整个数据集, 表现出良好的鲁棒性和较高的定位精度。
|
下载CSV 表 6 RuRoC数据集室内小尺度实验结果 Table 6 Indoor small scale experimental results of RuRoC dataset |
|
Download:
|
| 图 9 序列V1_01跟踪结果 Fig. 9 Tracking results of sequence V1_01 | |
|
Download:
|
| 图 10 序列V1_02跟踪结果 Fig. 10 Tracking results of sequence V1_02 | |

|
Download:
|
| 图 11 序列V1_03跟踪结果 Fig. 11 Tracking results of sequence V1_03 | |
针对单目视觉里程计在相机快速运动时鲁棒性较低的问题, 本文提出一种改进的单目视觉里程计算法。通过结合基于树结构的特征匹配算法、基于前n帧的位姿粗估计方法、实时地图扩展更新策略以及基于视差的权重矩阵估计方法, 使得算法在相机快速或剧烈运动下取得较高的定位精度和鲁棒性。在大尺度室外数据集KITTI和小尺度室内数据集EuRoC中进行实验, 结果表明, 该算法的跟踪频率为18 Hz~22 Hz, 具有较好的实时性, 在平缓的直线运动中, 本文算法与无回环线程的ORB-SLAM算法具有相近的精度, 在曲线或剧烈运动中, 本文算法取得了更高的鲁棒性和定位精度。下一步将考虑卷帘快门对定位结果的影响, 探究并消除由于同一帧图像各行曝光时刻不一致而引入的误差。
| [1] |
NISTER D, NARODITSKY O, BERGEN J.Visual odometry[C]//Proceedings of 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Washington D.C., USA: IEEE Press, 2004: 125-139.
|
| [2] |
FRAUNDORFER F, SCARAMUZZA D. Visual odometry, part Ⅱ:matching, robustness, optimization, and applications[J]. IEEE Robotics and Automation Magazine, 2012, 19(2): 78-90. DOI:10.1109/MRA.2012.2182810 |
| [3] |
CHEN Y J, YANG G L, JIANG Y X, et al.Monocular visual odometry based on trifocal tensor constraint[EB/OL].[2019-10-10].https://iopscience.iop.org/article/10.1088/1742-6596/976/1/012002/pdf.
|
| [4] |
CADENA C, CARLONE L, CARRILLO H, et al. Past, present, and future of simultaneous localization and mapping:toward the robust-perception age[J]. IEEE Transactions on Robotics, 2016, 32(6): 1309-1332. DOI:10.1109/TRO.2016.2624754 |
| [5] |
CHEN Yalan, ZHOU Yimin, LÜ Qin, et al.A review of V-SLAM[C]//Proceedings of 2018 IEEE International Con-ference on Information and Automation.Washington D.C., USA: IEEE Press, 2018: 603-608.
|
| [6] |
LIU Haomin, ZHANG Guofeng, BAO Hujun. A survey of monocular simultaneous localization and mapping[J]. Journal of Computer-Aided Design and Computer Graphics, 2016, 28(6): 855-868. (in Chinese) 刘浩敏, 章国锋, 鲍虎军. 基于单目视觉的同时定位与地图构建方法综述[J]. 计算机辅助设计与图形学学报, 2016, 28(6): 855-868. |
| [7] |
DAVISON A J, REID I D, MOLTON N D, et al. MonoSLAM:real-time single camera SLAM[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(6): 1052-1067. DOI:10.1109/TPAMI.2007.1049 |
| [8] |
BATTISTELLI G, CHISCI L. Stability of consensus extended Kalman filter for distributed state estimation[J]. Automatica, 2016, 68: 169-178. DOI:10.1016/j.automatica.2016.01.071 |
| [9] |
KLEIN G, MURRAY D.Parallel tracking and mapping for small AR workspaces[C]//Proceedings of the 6th IEEE and ACM International Symposium on Mixed and Augmented Reality.Washington D.C., USA: IEEE Press, 2007: 1-10.
|
| [10] |
MUR-ARTAL R, MONTIEL J M M, TARDOS J D. ORB-SLAM:a versatile and accurate monocular SLAM system[J]. IEEE Transactions on Robotics, 2015, 31(5): 1147-1163. DOI:10.1109/TRO.2015.2463671 |
| [11] |
ENGEL J, SCHÖPS T, CREMERS D.LSD-SLAM: large-scale direct monocular SLAM[M].Berlin, Germany: Springer, 2014.
|
| [12] |
YUAN Meng, LI Aihua, ZHENG Yong, et al. Point-line feature fusion in monocular visual odometry[J]. Laser and Optoelectronics Progress, 2018, 55(2): 366-373. (in Chinese) 袁梦, 李艾华, 郑勇, 等. 点线特征融合的单目视觉里程计[J]. 激光与光电子学进展, 2018, 55(2): 366-373. |
| [13] |
YUAN Meng, LI Aihua, CUI Zhigao, et al. Monocular vision odometry based on the improved 3D ICP matching[J]. Robot, 2018, 40(1): 56-63. (in Chinese) 袁梦, 李艾华, 崔智高, 等. 基于改进的3维ICP匹配的单目视觉里程计[J]. 机器人, 2018, 40(1): 56-63. |
| [14] |
FORSTER C, PIZZOLI M, SCARAMUZZA D.SVO: fast semi-direct monocular visual odometry[C]//Proceedings of 2014 IEEE International Conference on Robotics and Automation.Washington D.C., USA: IEEE Press, 2014: 15-22.
|
| [15] |
ENGEL J, KOLTUN V, CREMERS D. Direct sparse odometry[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(3): 611-625. DOI:10.1109/TPAMI.2017.2658577 |
| [16] |
FISCHLER M A, BOLLES R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J]. Readings in Computer Vision, 1987, 24(6): 726-740. |
| [17] |
HERRERA C D, KIM K, KANNALA J, et al.DT-SLAM: deferred triangulation for robust SLAM[C]//Proceedings of 2014 International Conference on 3D Vision.Washington D.C., USA: IEEE Press, 2014: 609-616.
|
| [18] |
PIRCHHEIM C, SCHMALSTIEG D, REITMAYR G.Handling pure camera rotation in keyframe-based SLAM[C]//Proceedings of 2013 IEEE International Symposium on Mixed and Augmented Reality.Washington D.C., USA: IEEE Press, 2013: 229-238.
|
| [19] |
GEIGER A, LENZ P, STILLER C, et al. Vision meets robotics:the KITTI dataset[J]. The International Journal of Robotics Research, 2013, 32(11): 1231-1237. DOI:10.1177/0278364913491297 |
| [20] |
BURRI M, NIKOLIC J, GOHL P, et al. The EuRoC micro aerial vehicle datasets[J]. The International Journal of Robotics Research, 2016, 35(10): 1157-1163. DOI:10.1177/0278364915620033 |
 2020, Vol. 46
2020, Vol. 46
