间隔理论[1]由VAPNIK等人于1995年提出, 其基于最小间隔最大化的原理, 能够从理论上有效地解释其他许多学习方法的泛化性。在间隔理论的基础上, 文献[2]提出了一种类似于boosting的算法Arc-gv, 该算法同样以最小间隔最大化的方式求解优化问题, 但泛化性能较差。研究人员发现这种算法虽然充分利用了最小间隔的重要性, 但是数据的间隔分布并不好。他们认为相比于最小间隔, 数据的间隔分布可能对泛化性的影响更大, 文献[3]对其进行了理论证明。并且, 文献[4]还将该思想应用到传统支持向量机(Support Vector Machine, SVM)分类中, 获得了更好的分类精度和泛化性能, 充分说明相比传统的最小间隔最大化的优化方法, 对间隔分布进行优化更加重要。
在现实的分类问题中, 由于人为或其他因素的影响, 数据往往会存在一定的噪声。如何对带有噪声的数据进行有效分类, 是一个值得研究的问题。然而, 传统的SVM对噪声数据不具有很好的鲁棒性, 这是因为传统SVM使用无界的铰链损失函数, 对于噪声数据会产生较大的损失值, 使SVM的分类超平面严重偏离最优超平面, 影响最终的分类效果。于是, 许多研究从改进损失函数角度出发, 提高SVM对噪声数据的鲁棒性。文献[5]在铰链损失的基础上提出了一种截断的铰链损失, 通过引入一个小于0的截断参数s, 使铰链损失有一个确定的界限, 解决了噪声数据带来较大损失的问题。通过最大化2个类之间的最小分位数距离, 文献[6]提出了弹球损失, 弹球损失是最大化2个类之间的分位数间距, 而不是最小间距, 由此提高了对属性噪声的识别性, 改善了分类性能。文献[6]在此基础上提出了一种截断的弹球损失(truncated pinball loss)。相比于最初的pinball损失, 文献[7]提出的损失函数增加了两段水平部分, 使得损失函数的值有一个固定的上界, 降低了噪声数据对算法性能的影响。
求解建立的SVM模型也是一个值得研究的问题。随机梯度下降(Stochastic Gradient Descent, SGD)算法是一阶优化方法, 广泛应用于各种优化问题中, 并衍生出许多优秀的算法, 如文献[8]提出的Pegasos算法, 该算法在每次迭代中随机选择一个样本计算梯度, 并以此代替全梯度。由于通常假设样本是独立同分布的, 从而随机抽取单个样本的目标函数的梯度是整个目标函数梯度的无偏估计, 进而可用每次迭代仅处理单个或部分样本的随机优化方法来代替批处理方法, 但是该方法存在方差, 随着迭代次数的增加, 方差也逐渐累加, 收敛速率不可避免地受到影响。为降低方差的影响, 文献[9]提出了减小方差的随机梯度(Stochastic Variance Reduction Gradient, SVRG)下降算法。该算法分为内外两层循环, 仅在外层循环计算全梯度, 降低了计算量。在内层循环中引入梯度修正项, 降低了方差对算法的影响, 提高了算法的性能。文献[10]在SVRG算法的基础上依据Nesterov的动量加速技巧, 提出了快速减小方差的随机梯度(Fast Stochastic Variance Reduced Gradient, FSVRG)下降[11]算法。FSVRG是SVRG的一个加速变种, 在每次内层迭代中引入了动量加速技巧, 不仅计算在当前迭代中的梯度值, 同时考虑了上一轮的梯度变化, 与SVRG相比提高了算法的收敛速度。此外, 在文献[12]提出的结构凸优化问题和文献[13]提出的经典的Katyusha算法以及文献[14]提出的加速随机镜像下降算法中均引入了动量加速技巧, 且都获得了较好的性能。
上述所提方法虽然可以有效地降低方差对算法的影响, 但是在每次迭代中均需要计算梯度, 求解梯度困难或者不能求解梯度的模型, 会增加额外的开销。因此, 文献[15]把零阶优化方法和减小方差策略相结合, 提出一种零阶减小方差的随机梯度(Zeroth Order-Stochastic Variance Reduced Gradient, ZO-SVRG)下降方法。ZO-SVRG不需要计算梯度的准确数值, 而是用函数值逼近梯度, 有效地解决了复杂模型不能计算梯度的问题, 具有较高的实用性。文献[16]基于零阶优化的思想, 结合交替方向乘子法, 提出一种在线的零阶交替方向乘子算法(ZOO-ADMM)。该算法既避免了梯度的计算, 又利用了交替乘子法能够处理复杂结构的优势, 经过理论分析和实验验证说明了所提方法的有效性。
为解决传统SVM对噪声敏感的问题, 本文通过引入间隔分布和新形式的损失函数, 提出一种基于动量加速零阶减小方差的鲁棒支持向量机(MA-ZOVR)。
1 相关工作对于一般的优化问题, 定义如下的样例空间:S={(x1, y1), (x2, y2), …, (xn, yn)}为给定的n个数据, xi∈
| $ \min F(\mathit{\boldsymbol{\omega }}) = \frac{\lambda }{2}\|\mathit{\boldsymbol{\omega }}\|{^2} + \frac{1}{n}\sum\limits_{i = 1}^n {\max } \left( {0,1 - {y_i}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i}} \right) $ | (1) |
其中,
在零阶优化方法中, 对于优化问题的梯度计算不再使用传统的方法, 而是直接使用函数值近似代替梯度, 避免了重复的梯度计算, 大幅降低了工作量。对于计算梯度困难的复杂模型, 零阶优化可以有效地提高算法性能。因此, 零阶优化广泛应用于机器学习领域, 并由此衍生出一系列算法。具有代表性的零阶优化算法是文献[12]提出的ZO-SVRG算法。ZO-SVRG算法分为内外双重循环, 在零阶优化的基础上结合了SVRG减小方差的策略。在每轮外层循环中, 定义一个向量
| $ G\left( {{\mathit{\boldsymbol{\omega }}_t}} \right) = \hat \nabla {F_i}\left( {{\mathit{\boldsymbol{\omega }}_t}} \right) - \hat \nabla {F_i}(\mathit{\boldsymbol{\tilde \omega }}) + \hat \nabla F(\mathit{\boldsymbol{\tilde \omega }}) $ | (2) |
其中, G(ωt)称为梯度修正项。
零阶梯度估计用函数值近似代替, 坐标梯度估计如下[15]:
| $ \hat \nabla {F_i}(\mathit{\boldsymbol{\omega }}) = \sum\limits_{l = 1}^d {\left( {\frac{1}{{2{\mu _l}}}} \right)} \left[ {{F_i}\left( {\mathit{\boldsymbol{\omega }} + {\mu _l}{\mathit{\boldsymbol{e}}_l}} \right) - {F_i}\left( {\mathit{\boldsymbol{\omega }} - {\mu _l}{\mathit{\boldsymbol{e}}_l}} \right)} \right]{\mathit{\boldsymbol{e}}_l} $ | (3) |
其中, el表示一个标准基向量, 在第l个坐标处为1, 其他坐标处为0, μl>0表示光滑参数。
ZO-SVRG算法如下:
算法1 ZO-SVRG算法
输入 外层迭代轮数S, 内层迭代次数T, 学习率η, 光滑参数μ
输出
初始化
1.for s=1, 2, …, S
2.
3. 计算全梯度
4. ω0=
5. for t=0, 1, …, T-1
6. 随机抽取一个样本i, 进行梯度更新
7. ωt+1=ωt-η(
8. end
9.
10.end
11.return
文献[17]指出Nesterov[10]的动量加速技巧可以加速随机减小方差算法的收敛, 能够使强凸问题和一般凸问题的收敛速度达到较高的水平。随机减小方差算法均分为内外双重循环, 引入动量加速技巧后, 每次内层迭代的梯度由式(4)、式(5)2个更新规则构成:
| $ {v_{t + 1}} = {v_t} - {\eta _s}\left( {\hat \nabla {F_i}\left( {{\mathit{\boldsymbol{\omega }}_t}} \right) - \hat \nabla {F_i}(\mathit{\boldsymbol{\tilde \omega }}) + \hat \nabla F(\mathit{\boldsymbol{\tilde \omega }})} \right) $ | (4) |
| $ {\mathit{\boldsymbol{\omega }}_{t + 1}} = \mathit{\boldsymbol{\tilde \omega }} + {\rho _s}\left( {{v_{t + 1}} - \mathit{\boldsymbol{\tilde \omega }}} \right) $ | (5) |
根据式(4)计算当前迭代中的梯度变化情况, 其中, vt+1为辅助变量, ηs为更新步长。
式(5)表示, 结合上一轮梯度的结果, 得出本次内层迭代最终的梯度更新规则。其中, ρs表示动量权重系数。
引入动量加速技巧后的梯度更新规则并不仅仅依赖于当前迭代的梯度变化情况, 并且考虑了上一轮的最终结果。所以, 计算当前迭代中的梯度时, 都会有一个之前梯度的作用。如果这次的梯度和上一轮的梯度方向相同, 则会因为之前的速度继续加速; 如果这次的梯度和上一轮的梯度方向相反, 则不增加或减少过多。因此, 引入动量加速技巧后, 会使梯度在每次的下降过程中减少摆动的幅度, 加速算法的收敛。
2 动量加速零阶减小方差的鲁棒SVM基于文献[4]的理论证明, 在本文中用间隔分布均值代替传统的最小间隔, 充分考虑每个样本的分布情况。间隔分布均值为:
| $ \frac{1}{n}\sum\limits_{i = 1}^n {{y_i}} {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i} $ | (6) |
此外, 传统SVM的损失函数为铰链损失。但由于铰链函数无界性的特点, 对于噪声数据会带来较大的损失, 使分类性能下降。因此, 为了降低噪声数据的影响, 结合指数函数的结构特点, 引入一种新形式的损失函数:
| $ \max \left( {0,\frac{{{{\rm{e}}^{2\left( {1 - {y_i}{\mathit{\boldsymbol{\omega }}^{{\rm{T}}{x_i}}}} \right)}} - 1}}{{{{\rm{e}}^{2\left( {1 - {y_i}{\mathit{\boldsymbol{\omega }}^{\left. {{\rm{T}}{x_i}} \right)}} + 1} \right.}}}}} \right) $ | (7) |
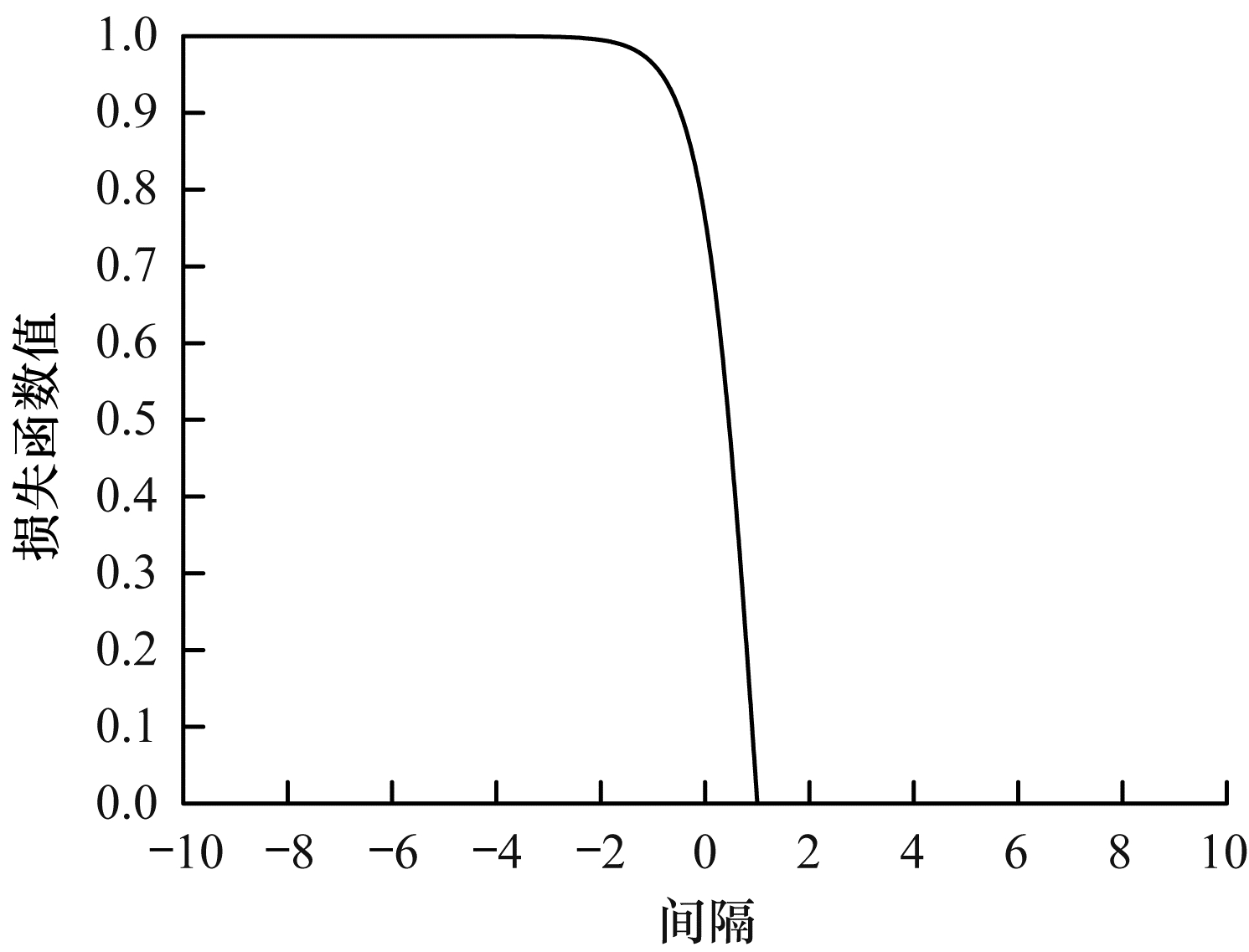
损失函数曲线如图 1所示。
|
Download:
|
| 图 1 损失函数曲线示意图 Fig. 1 Schematic diagram of loss function curve | |
在图 1中, 横坐标表示间隔, 即yiωTxi, 一般又将其称为函数间隔。在SVM的分类任务中, 可以通过函数间隔的正负来判定或表示样本分类的正确性; 纵坐标表示对应的损失函数值。下文对损失函数进行具体的分析:
1) 当1-yiωTxi=0时, yiωTxi=1>0, 样本正确分类, 对应的损失值为0。
2) 当1-yiωTxi < 0时, yiωTxi>1>0, 样本正确分类, 对应的损失值为0。
3) 当1-yiωTxi>0时, yiωTxi < 1, 这时存在2种情况:
(1) 当0 < yiωTxi < 1时, 样本位于分类间隔内。
(2) 当yiωTxi < 0时, 样本错误分类。
在3)中的2种情况表示的是噪声数据的分类状态。可以明显地看出噪声数据的损失值限制在了[0, 1]之间, 避免了出现噪声数据带来过大损失的情况, 从而降低了噪声数据对分类性能的影响。
2.1 线性MA-ZOVR算法通过引入间隔分布均值以及新的损失函数, 在线性输入空间建立新的优化模型如下:
| $ \begin{array}{l} \min F(\mathit{\boldsymbol{\omega }}) = - \frac{\lambda }{n}\sum\limits_{i = 1}^n {{y_i}} {\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{n}\sum\limits_{i = 1}^n {\max } \left( {0,\frac{{{{\rm{e}}^{2\left( {1 - {y_i},{\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i}} \right)}} - 1}}{{{{\rm{e}}^{2\left( {1 - {y_j},{\mathit{\boldsymbol{\omega }}^{\rm{T}}}{x_i}} \right)}} + 1}}} \right) \end{array} $ | (8) |
对于优化模型的求解, 基于零阶优化减小方差的思想, 配合动量加速技巧, 提出一种基于动量加速零阶减小方差(MA-ZOVR)算法。
在线性MA-ZOVR算法中, 首先对梯度进行估计, 改变传统的梯度计算方式, 通过式(3)坐标梯度估计法, 计算出函数值并近似代替梯度。为降低方差对算法性能的影响, 引入了式(2)的梯度修正项。最后结合动量加速技巧, 在内层迭代中使用式(4)和式(5)进行梯度的更新。
线性MA-ZOVR算法如算法2所示。
算法2 线性MA-ZOVR算法
输入 外层迭代轮数S, 内层迭代次数T, 光滑参数μ, 正则化参数λ
输出
初始化 v0=
1.for s=1, 2, …, S
2.
3. 计算全梯度
4.
5. ω0=ρsv0+(1-ρs)
6. for t=0, 1, …, T-1
7. 随机抽取一个样本i进行梯度更新
8. vt+1=vt-ηs(
9. ωt+1=
10. end for
11.
12. v0=vT
13.end for
14.
算法中的第8步、第9步为梯度更新规则, 也是关键的步骤。其中
在非线性输入空间, 定义如下的优化问题:
| $ \begin{array}{l} \min F(\mathit{\boldsymbol{\omega }}) = - \frac{\lambda }{n}\sum\limits_{i = 1}^n {{y_i}} {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{x_i}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{n}\sum\limits_{i = 1}^n {\max } \left( {0,\frac{{{{\rm{e}}^{2\left( {1 - {y_i}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{x_i}} \right)} \right)}} - 1}}{{{{\rm{e}}^{2\left( {1 - {y_i}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{x_i}} \right)} \right)}} + 1}}} \right) \end{array} $ | (9) |
一般地, 在非线性特征空间, 优化问题中φ(xi)的维数很高, 求解非常复杂。本文通过表示定理[8, 20]对式(9)进行变形:
| $ \mathit{\boldsymbol{\omega }} = \sum\limits_{i = 1}^n {{\alpha _i}} \varphi \left( {{x_i}} \right) = \mathit{\boldsymbol{X\alpha }} $ | (10) |
其中, α=[α1, α2, …, αn]T, X=[φ(x1), φ(x2), …, φ(xn)]。根据式(10)可得:
| $ \begin{array}{l} {y_i}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\varphi \left( {{x_i}} \right) = {y_i}{(\mathit{\boldsymbol{X\alpha }})^{\rm{T}}}\varphi \left( {{x_i}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{y_i}{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\varphi \left( {{x_i}} \right) = {y_i}{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{G_i} \end{array} $ |
其中, G=XTX表示核矩阵, Gi表示G的第i列, 式(8)可以表示为:
| $ \begin{array}{l} \min F(\alpha ) = - \frac{\lambda }{n}\sum\limits_{i = 1}^n {{y_i}} {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{G_i} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{n}\sum\limits_{i = 1}^n {\max } \left( {0,\frac{{{{\rm{e}}^{2\left( {1 - {y_j}{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{G_i}} \right)}} - 1}}{{{{\rm{e}}^{2\left( {1 - {y_j}{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{G_i}} \right)}} + 1}}} \right) \end{array} $ | (11) |
对于变形后的优化问题式(11), 不再将其转换成对偶形式, 而是使用提出的非线性MA-ZOVR算法直接求解。非线性MA-ZOVR算法和2.1节提到的线性算法有着相同的框架, 不同是非线性MA-ZOVR算法优化变量为α引入了核运算。
非线性MA-ZOVR算法如算法3所示。
算法3 非线性MA-ZOVR算法
输入 外层迭代轮数S, 内层迭代次数T, 光滑参数μ, 正则化参数λ
输出
初始化 v0=
1.for s=1, 2, …, S
2.
3. 计算全梯度
4.
5. α0=ρsv0+(1-ρs)
6. for t=0, 1, …, T-1
7. 随机抽取一个样本i, 进行梯度更新
8. vt+1=vt-ηs(
9. αt+1=
10. end for
11.
12. v0=vT
13. end for
14.
在给出MA-ZOVR算法的收敛性结论前, 对MA-ZOVR算法用到的相关知识进行总结如下:
1) 整体框架:使用零阶减小方差优化框架, 降低了方差的影响, 同时避免了重复的梯度计算。
2) 梯度计算方法:使用坐标梯度估计[12, 15]。虽然多了O(d)次的函数查询(计算函数值), 但是可以获得更精确的梯度估计。
3) 梯度更新方法:在减小方差的基础上结合动量加速技巧[18, 21-22], 加速算法的收敛。
在考虑零阶优化的前提下, 根据文献[15]关于坐标梯度估计的收敛性分析(定理3)以及文献[18]中关于动量加速技巧的收敛性分析(定理1), 可以得出本文提出的MA-ZOVR算法的收敛速度为
本节验证本文提出的动量加速零阶减小方差的鲁棒SVM(MA-ZOVR)算法的性能, 主要从以下5个方面进行实验:
1) 抗噪性实验:进行线性MA-ZOVR算法和非线性MA-ZOVR算法的抗噪性实验。
2) 模块化实验:分别验证新的求解方法和新的优化模型的有效性。
3) 方差分析实验:针对非线性情况, 对比本文提出的算法和标准随机梯度下降算法(SGD), 验证算法减小方差策略的有效性。
4) 收敛速度分析实验:针对非线性情况, 对比本文的动量加速零阶减小方差算法和原始的零阶减小方差(ZO-SVRG)算法, 验证算法收敛速度的加速。
5) 参数分析实验:分析实验中的主要参数对算法精度的影响。
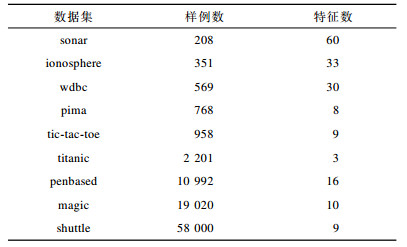
实验程序运行环境为Matlab R2016a。实验数据来源于KEEL网站(训练集和测试集的比例均为4:1), 主要分为2个部分:第1部分为常规噪声数据集, 依次选取含有0%、5%、10%和15%属性噪声的数据进行实验; 第2部分为相对较大规模的标准数据集, 为了验证算法的抗噪性, 依次对这几个数据集加入0%、5%、10%和15%均值为0及方差为0.5的高斯噪声。实验数据集如表 1所示。
|
下载CSV 表 1 实验数据集 Table 1 Experimental datasets |
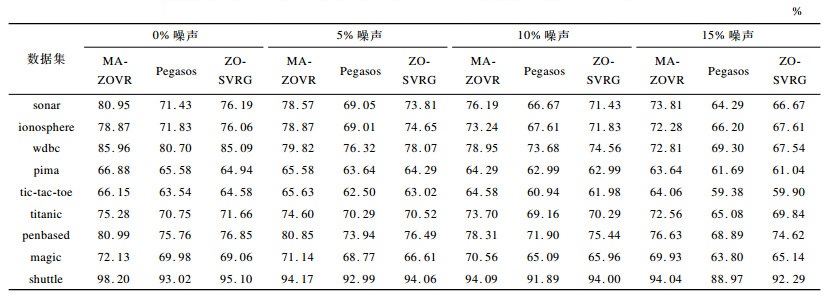
本节进行线性MA-ZOVR算法和非线性MA-ZOVR算法的抗噪性实验。为了使实验效果更加明显, 下面给出本文提出的MA-ZOVR算法和传统的SVM算法(文献[8]中的Pegasos算法求解优化问题1以及原始零阶减小方差算法, 文献[15]中的ZO-SVRG算法求解优化问题1)的测试分类结果。下文所给结果均为五折交叉实验的平均值。线性算法的比较结果如表 2所示。
|
下载CSV 表 2 不同线性算法分类准确率比较 Table 2 Comparison of classification accuracy of different linear algorithms |
从表 2可以看出, 在给定的9组不同噪声比的数据集中, 本文提出的线性MA-ZOVR算法与线性Pegasos算法以及线性ZO-SVRG算法相比, 均具有较高的准确率, 这说明了本文提出的算法有效地提高了SVM的抗噪性, 具有较高的分类精度。另外, 从给出的结果还可以看出, 随着数据噪声百分比的增大, 分类准确率随之降低。
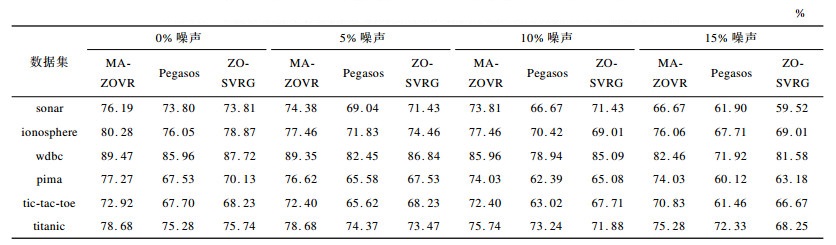
由于非线性MA-ZOVR算法涉及到了核矩阵的运算, 因此在处理较大规模数据时, 运行时间过长。为了提高实验效率, 在常规数据集上进行非线性MA-ZOVR算法的抗噪性对比实验。非线性MA-ZOVR算法、非线性Pegasos算法以及非线性ZO-SVRG算法的实验结果如表 3所示, 其中均使用高斯核函数。
|
下载CSV 表 3 不同非线性算法分类准确率比较 Table 3 Comparison of classification accuracy of different nonlinear algorithms |
从表 3可以看出, 在给定的不同噪声比的6组数据集中, 本文提出的非线性MA-ZOVR算法与非线性Pegasos算法以及非线性ZO-SVRG算法相比, 均具有较高的准确率, 这说明非线性MA-ZOVR算法的抗噪性能好, 能够改善传统SVM的不足, 降低了噪声数据对分类效果的影响。
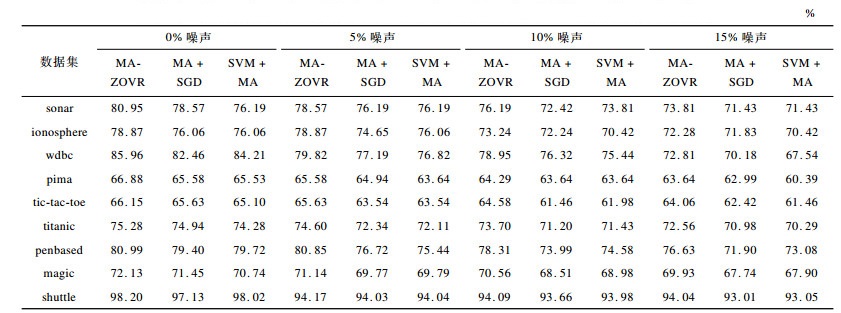
3.2 模块化实验本文提出的MA-ZOVR算法包括对优化模型和求解方法2个方面的改进。为更好地说明问题, 下文进行模块化实验。模块化实验1:对改进后的优化模型式(7)、式(10)分别使用传统的随机梯度下降的求解方法, 记为MA+SGD; 模块化实验2:对传统的SVM模型式(1)使用提出的MA-ZOVR优化求解方法(包括线性和非线性), 记为SVM+MA。线性算法模块化实验结果如表 4所示。
|
下载CSV 表 4 不同线性算法模块化实验结果比较 Table 4 Comparison of modularization experimental results of different linear algorithms |
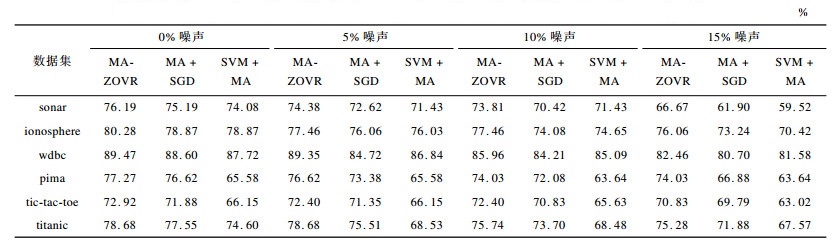
从表 4可以看出, 在给定的不同噪声比的9组数据集中, 本文提出的线性MA-ZOVR算法的精度优于实验1的精度, 这说明了在线性情况下本文提出的求解方法的有效性。同样, 根据与实验2结果的对比也可以看出, 在线性情况下本文提出的优化模型的有效性。非线性MA-ZOVR算法的模块化实验结果如表 5所示。从表 5可以看出, 在给定的不同噪声比的6组数据集中, 本文提出的非线性MA-ZOVR算法分类精度均高于实验1和实验2。按照上述的分析方法, 分别验证了在非线性情况下本文提出的求解方法和优化模型的有效性。
|
下载CSV 表 5 不同非线性算法模块化实验结果比较 Table 5 Comparison of modularization experimental results of different nonlinear algorithms |
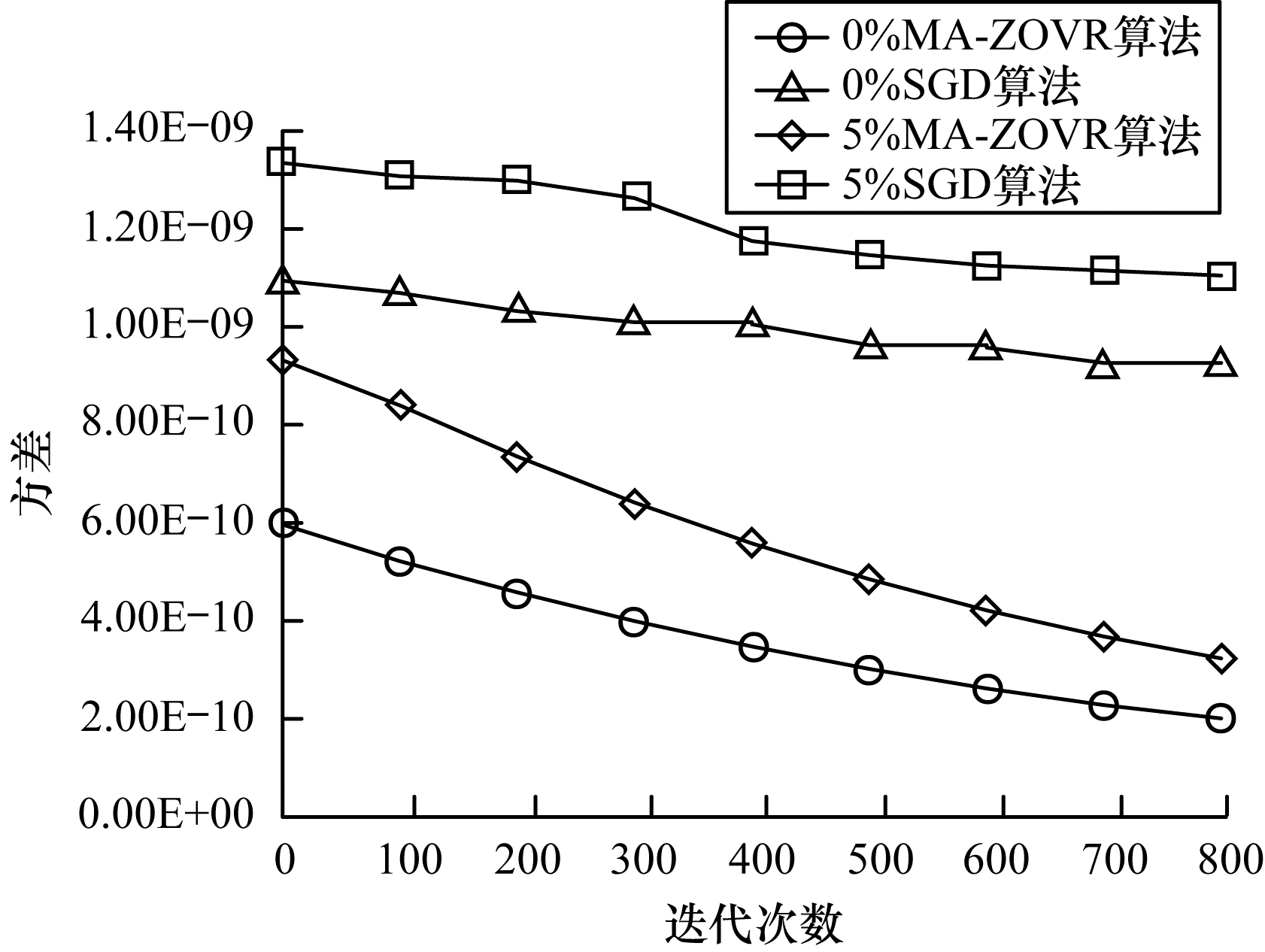
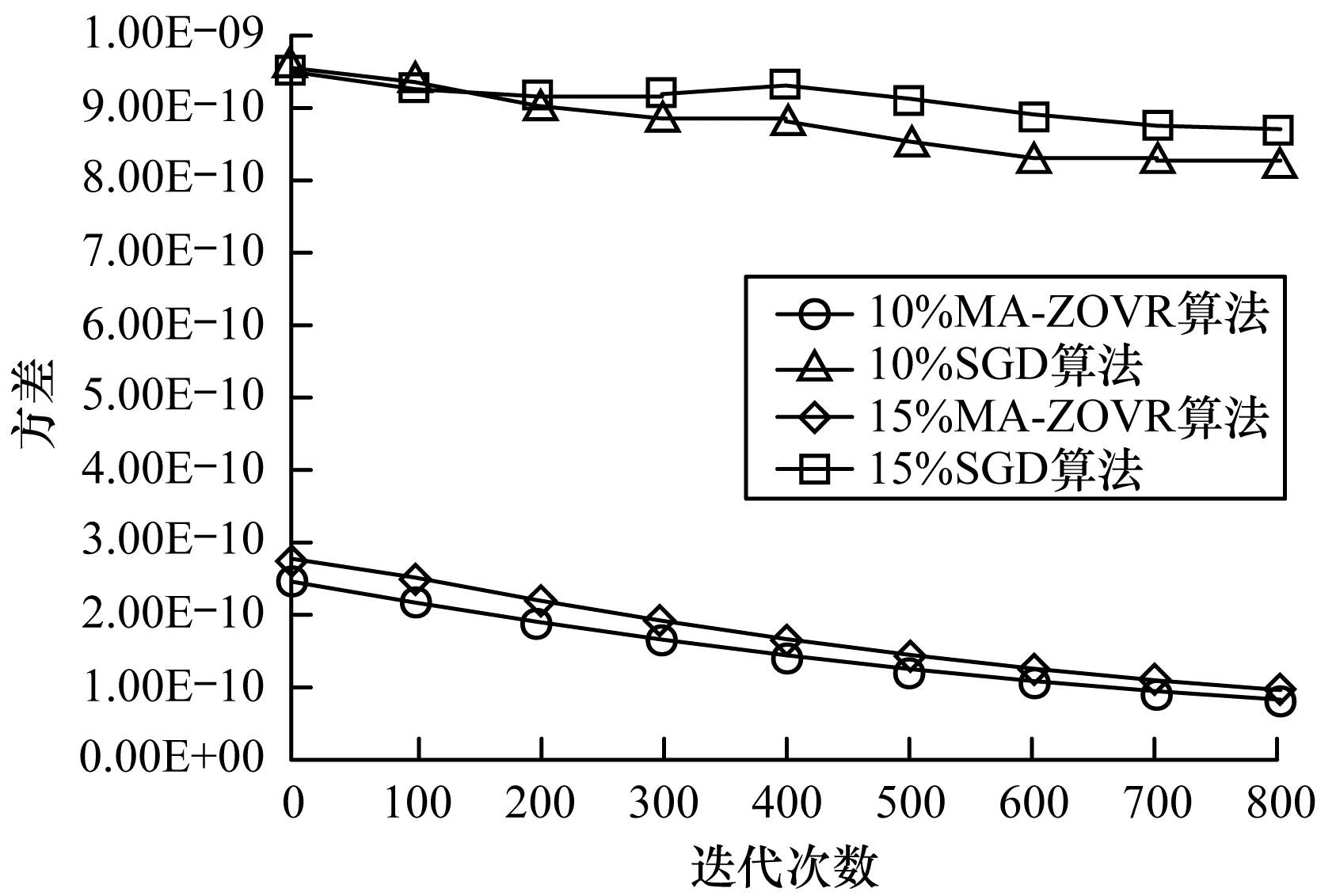
本节进行非线性MA-ZOVR算法和传统随机梯度下降(Stochastic Gradient Descent, SGD)算法的方差分析实验。图 2和图 3为MA-ZOVR算法和传统SGD算法对不同噪声比的wdbc数据集进行分类的方差对比。
|
Download:
|
| 图 2 不同噪声比(0%, 5%)的方差对比结果 Fig. 2 Variance comparison results of different noise ratios (0%, 5%) | |
|
Download:
|
| 图 3 不同噪声比(10%, 15%)的方差对比结果 Fig. 3 Variance comparison results of different noise ratios (10%, 15%) | |
从图 2和图 3可以看出, 在迭代过程中对于不同噪声比的实验数据, 随机梯度下降算法的方差一直维持一个比较大的值, 下降幅度较小。对比结果可以看出, 本文提出的MA-ZOVR算法的方差较小, 且随着迭代的进行逐步降低, 最后减小到一个接近于零的定值, 表明本文算法可以有效地对方差进行修正。
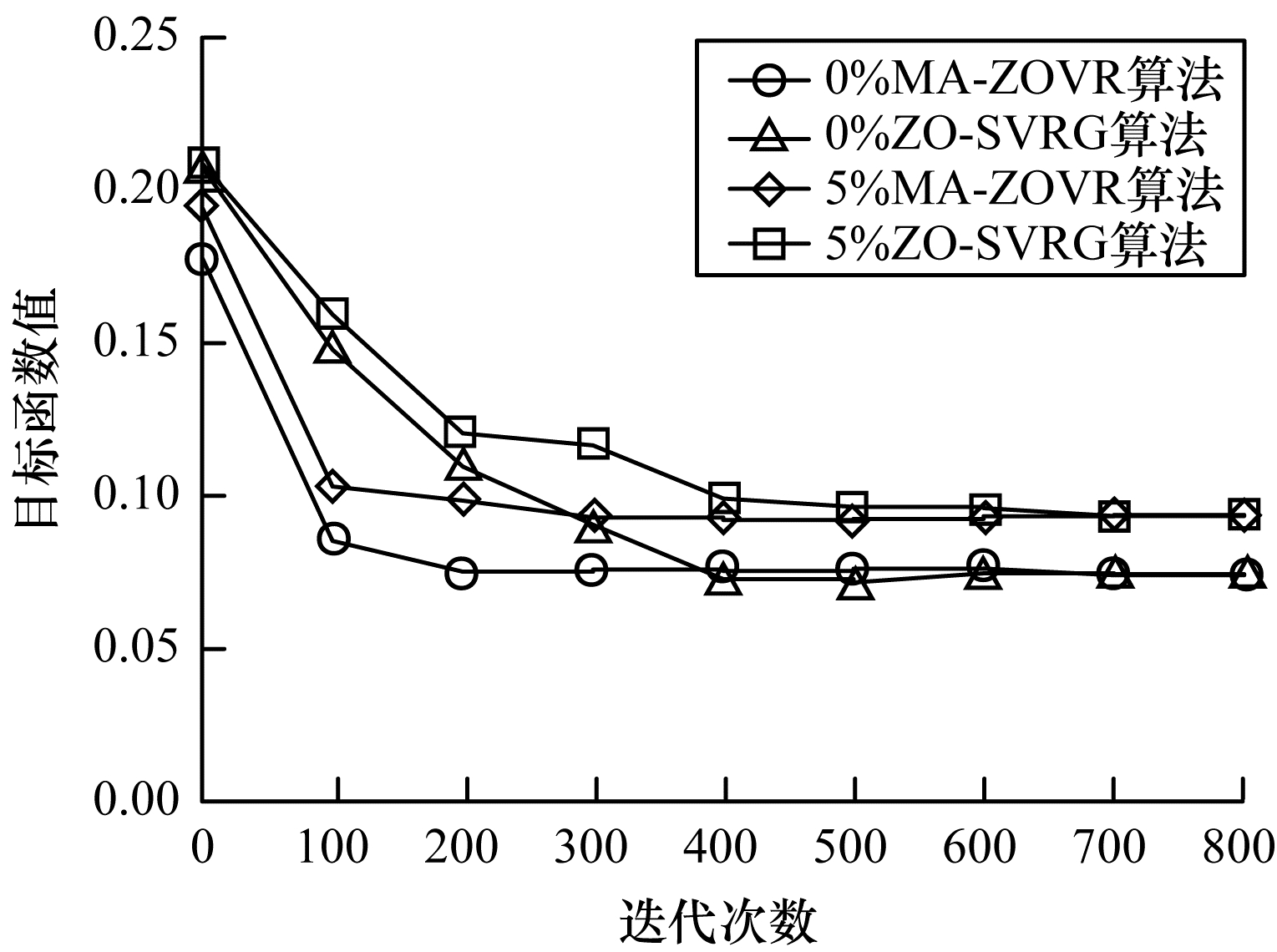
3.4 收敛速度分析实验本节进行非线性MA-ZOVR算法和非线性ZO-SVRG算法的收敛速度对比实验。图 4和图 5为2种方法对不同噪声比的ionosphere数据进行分类的收敛速度对比。
|
Download:
|
| 图 4 不同噪声比(0%, 5%)的目标函数值 Fig. 4 Objective function values of different noise ratios (0%, 5%) | |
|
Download:
|
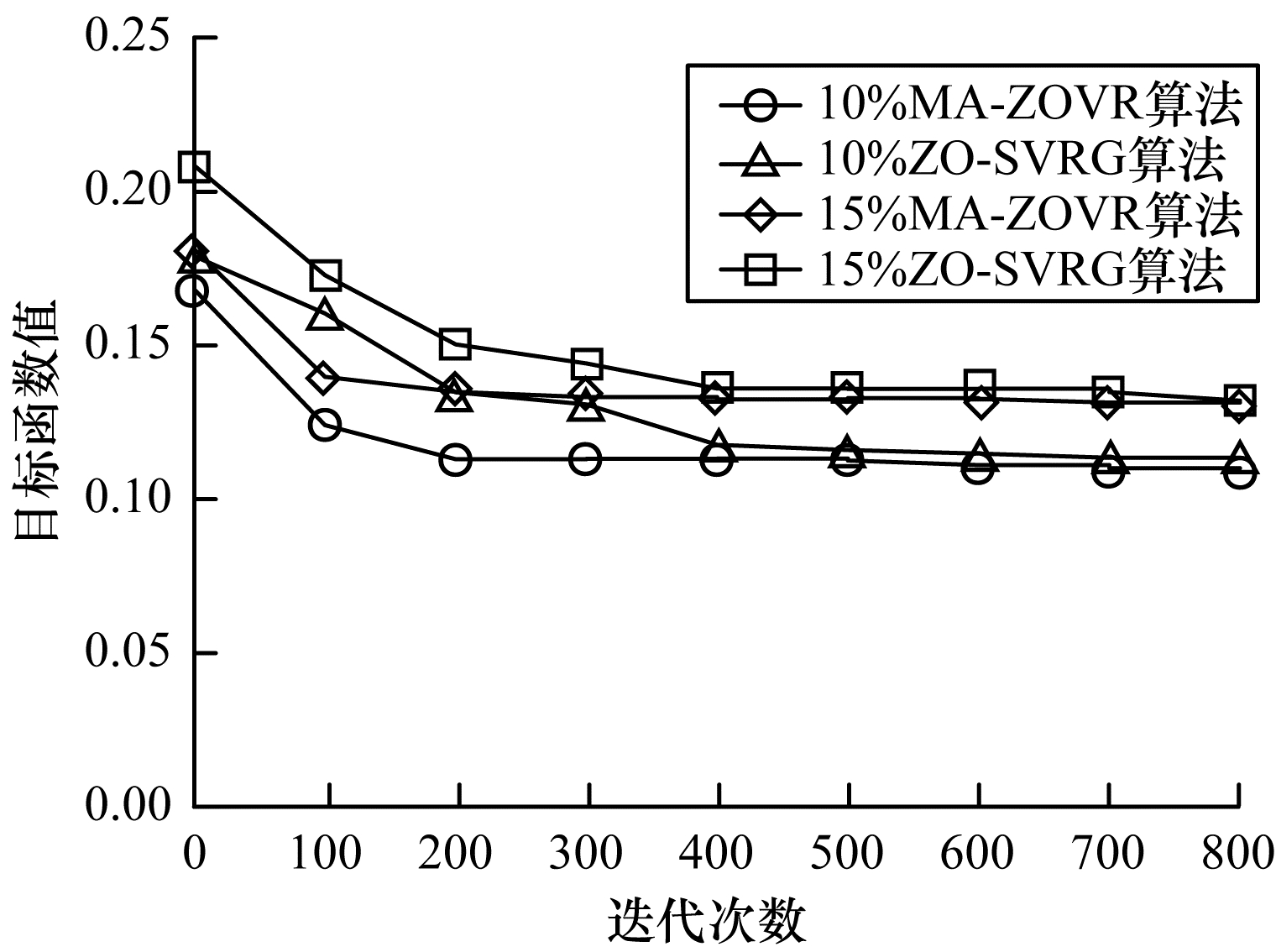
| 图 5 不同噪声比(10%, 15%)的目标函数值 Fig. 5 Objective function values of different noise ratios (10%, 15%) | |
从图 4和图 5可以看出, 对于不同百分比的噪声数据, 使用本文提出的MA-ZOVR算法进行求解时, 前200次迭代过程中函数值逐步减小, 在200次以后函数值逐渐趋
近于一个定值; 对比结果可以看出, 原始的ZO-SVRG算法在前400次迭代中函数值一直处于减小状态, 直到400次之后函数值才逐渐趋于稳定, 表明本文算法通过引入动量加速技巧, 有效地提高了算法的收敛速度。
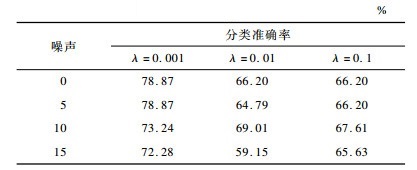
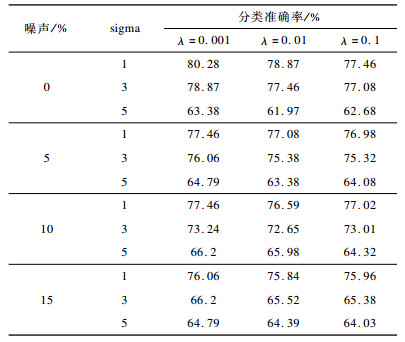
3.5 参数分析实验本节进行线性MA-ZOVR算法和非线性MA-ZOVR算法的参数分析实验。对于线性MA-ZOVR算法主要分析正则化参数λ对分类精度的影响; 对于非线性MA-ZOVR算法分析正则化参数λ和高斯核函数的宽度sigma两者共同对分类精度的影响。表 6、表 7给出不同噪声比的ionosphere数据分类的准确率。
|
下载CSV 表 6 线性MA-ZOVR算法分类准确率 Table 6 Classification accuracy of linear MA-ZOVR algorithm |
|
下载CSV 表 7 非线性MA-ZOVR算法分类准确率 Table 7 Classification accuracy of nonlinear algorithm MA-ZOVR |
对表 6进行横向对比, 在固定数据噪声比的条件下, 根据分类精度可以看出, 当参数λ=0.001时的分类效果较好。
首先对表 7进行横向对比, 在固定噪声比和sigma的条件下, 根据分类精度可以看出, 对于给定的不同λ值, 分类效果差异不大, 当λ=0.001时分类效果稍好于其他的取值; 其次对表 7进行纵向对比, 在固定噪声比和λ=0.001的条件下, 根据结果可得, 当sigma=1时分类效果较好。因此, 当参数sigma=1, λ=0.001时分类性能最优。
4 结束语为提高SVM的抗噪性, 本文提出一种基于动量加速零阶减小方差的鲁棒SVM算法。通过引入间隔均值项和指数形式的损失函数建立新的优化模型, 并在零阶减小方差的基础上引入动量加速技术求解优化模型。实验结果表明, 该方法能够有效提高SVM的抗噪性, 降低在迭代中累积的方差, 同时加快算法的收敛速度。下一步将在本文研究的基础上, 结合L1正则化项, 设计新的算法对带有噪声数据分类问题的稀疏化进行研究。
| [1] |
VAPNIK V N. The nature of statistical learning theory[M]. Berlin, Germany: Springer, 1995.
|
| [2] |
GAO Wei, ZHOU Zhihua. On the doubt about margin explanation of boosting[J]. Artificial Intelligence, 2013, 203(2): 1-18. |
| [3] |
ZHANG Teng, ZHOU Zhihua.Large margin distribution machine[C]//Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York, USA: ACM Press, 2014: 313-322.
|
| [4] |
WU Chao, LIU Yufeng. Robust truncated hinge loss support vector machines[J]. Journal of the American Statistical Association, 2007, 102(479): 974-983. DOI:10.1198/016214507000000617 |
| [5] |
HUANG Xiaolin, SHI Lei. Support vector machine classifier with pinball loss[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(5): 984-997. DOI:10.1109/TPAMI.2013.178 |
| [6] |
YANG Liming, DONG Hongwei. Support vector machine with truncated pinball loss and its application in pattern recognition[J]. Chemometrics and Intelligent Laboratory Systems, 2018, 177(2): 89-99. |
| [7] |
SHALEV-SHWARTZ S, SINGER Y. PEGASOS:primal estimated sub-gradient solver for SVM[J]. Mathematical Programming, 2011, 127(1): 3-30. |
| [8] |
JOHNSON R, ZHANG T. Accelerating stochastic gradient descent using predictive variance reduction[J]. News in Physiological Sciences, 2013, 1(3): 315-323. |
| [9] |
NESTEROV Y.Introductory lectures on convex optimization: a basic course[M].Boston, USA: Kluwer Academic Public, 2004.
|
| [10] |
SHANG Fanhua, LIU Yuanyuan.Fast stochastic variance reduced gradient method with momentum acceleration for machine learning[EB/OL].[2019-09-10].https://www.researchgate.net/publication.
|
| [11] |
TSENG P. Approximation accuracy, gradient methods, and error bound for structured convex optimization[J]. Mathematical Programming, 2010, 125(2): 263-295. DOI:10.1007/s10107-010-0394-2 |
| [12] |
ZHU Zeyuan.Katyusha: the first direct acceleration of stochastic gradient methods[C]//Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing.New York, USA: ACM Press, 2017: 1200-1205.
|
| [13] |
NGUYEN V C, XU Huan. Accelerated stochastic mirror descent algorithms for composite non-strongly convex optimization[J]. Journal of Optimization Theory and Applications, 2019, 18(2): 541-566. |
| [14] |
LIU S, KAILKHURA B.Zeroth-order stochastic variance reduction for nonconvex optimization[C]//Proceedings of the 32nd Conference on Neural Information Processing Systems.Washington D.C., USA: IEEE Press, 2018: 1-26.
|
| [15] |
LIU Shijia, CHEN Jie.Zeroth-order online alternating direction method of multipliers: convergence analysis and applications[C]//Proceedings of the 21st International Conference on Artificial Intelligence and Statistics.Washington D.C., USA: IEEE Press, 2018: 288-297.
|
| [16] |
ZHU Zeyuan.Katyusha: accelerated variance reduction for faster SGD[EB/OL].[2019-09-10].https://arxiv.org/abs/1603.05953v1.
|
| [17] |
SHANG Fanhua, ZHOU Kaiwen. VR-SGD:a simple stochastic variance reduction method for machine learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2018, 32(1): 188-202. |
| [18] |
CHEN Fanyong, ZHAN Jing. Large cost-sensitive margin distribution machine for imbalanced data classification[J]. Neurocomputing, 2017, 224(8): 45-57. |
| [19] |
ZHOU Yuhang, ZHOU Zhihua. Cost-sentive large margin distribution machine[J]. Journal of Computer Research and Development, 2016, 53(9): 1964-1970. (in Chinese) 周宇航, 周志华. 代价敏感大间隔分布学习机[J]. 计算机研究与发展, 2016, 53(9): 1964-1970. |
| [20] |
TAO Wei, PAN Zhisong. The individual convergence of projected subgradient methods using the Nesterov's step-size stratey[J]. Chinese Journal of Computers, 2018, 41(1): 164-176. (in Chinese) 陶蔚, 潘志松. 使用Nesterov步长策略投影次梯度方法的个体收敛性[J]. 计算机学报, 2018, 41(1): 164-176. |
| [21] |
CHEN Yujia, TAO Wei. Optimal individual convergence rate of the Heavy-Ball-Based momentum methods[J]. Journal of Computer Research and Development, 2019, 56(8): 1686-1694. (in Chinese) 程禹嘉, 陶蔚. Heavy-Ball型动量方法的最优个体收敛速率[J]. 计算机研究与发展, 2019, 56(8): 1686-1694. |
 2020, Vol. 46
2020, Vol. 46
