开放科学(资源服务)标志码(OSID):
信息粒化[1-2]是在问题求解空间中通过给定粒化策略将复杂数据转化为信息粒集合的构造性过程。作为粒计算的前提和关键,信息粒化研究进一步推动了智能信息领域的理论创新,在知识发现、海量数据挖掘、复杂问题求解等领域具有广泛的应用前景[1]。为解决模糊不可分的复杂问题,从而进行有效的问题分析及知识表示[3],PEDRYCZ等人以颗粒的形式划分模糊信息并根据现有依据形成“可信”粒子,提出了基于可信粒度准则的两阶段信息粒化框架[4-5]。第一阶段通过无监督学习的聚类分析方法,由原始数据形成数据集结构的雏形;第二阶段在监督模式下基于数据类簇构建信息颗粒,捕获数据集的核心结构,从而构建更综合和全面的粒度结构,使最后所生成颗粒原型的整体性能更佳[5]。
在两阶段粒化框架中,聚类既是粒化的手段,又是粒化的基础。用于粒化的聚类算法大体分为硬聚类和软聚类两类。C-Means硬聚类(Hard C-Means clustering,HCM) [1, 5-6]算法要求所有数据对象明确划分到确定的类簇,因此,在处理交叉类簇的重叠区域时易产生大量误分样本而影响粒子质量。模糊C均值(Fuzzy C-Means,FCM)[7-8]是最常见的软聚类算法,考虑到模糊隶属函数设计的主观因素,近年来粗糙C均值(Rough C-Means,RCM)[9]聚类算法得到快速发展。此后,将模糊集与粗糙集优势互补的模糊粗糙C均值(Fuzzy Rough C-Means,FRCM)[10]聚类算法也受到广泛关注。为提高对不确定性问题的描述能力,文献[11]将一般模糊集(称之为一型)扩展到二型模糊集,以主、次两级隶属函数共同描述模糊语言的“模糊程度”,但时间复杂度大幅增加。文献[12-13]通过默认次级隶属度取常数1,将二型模糊集简化为区间二型模糊集,以降低运算复杂度,这不仅增强了对不确定性信息的描述能力,而且也避免了算法的运算量呈指数级增长,同时还为边界交叉的不确定数据在两阶段信息粒化下的聚类分析提供了新思路。
信息粒化框架的第二阶段基于可信粒度准则构造综合考虑覆盖度和独特性的粒化函数,得到形成“可信”信息颗粒的解决方案。根据粒化依据,通常设计与粒子样本个数或权重呈正相关的函数来描述粒子的覆盖度,而反映粒子语义的独特性则正相反,其统一利用区间长度相关的非递增函数进行度量。目前被使用较多的粒化函数有余弦函数[14]、指数函数[15-17]、基于区间比值的线性函数[18-20]、基于区间与衰减参数的积分函数[21-23]等。文献[15-17]利用指数函数表述粒子的独特性,函数在X轴正半轴区域的变化趋势充分反映了粒子随区间长度增加语义不断衰减的非递增特性,通过指数系数
为解决多类簇交叉且分布不均衡数据的信息粒化问题,本文提出一种结合区间二型FRCM聚类与混合度量的两阶段信息粒化算法。在第一阶段,依据可信粒度准则,基于区间二型FRCM算法对不平衡数据进行聚类分析,在有效提升分析精度的同时,获取类簇形式的初始信息粒;在第二阶段,采用混合度量方法,以数据分布的疏密程度表述粒子内部的空间结构,以区间大小刻画粒子的区域范围,从而在充分描述粒子特性的同时,清晰体现粒子结构,最终获得客观的划分方案,形成合理的粒子区间。
1 相关知识 1.1 基于模糊集与粗糙集的C均值聚类在可信粒度准则的两阶段粒化框架中,聚类分析不仅被视为构建粒度原型的先决条件,而且还被作为揭示数据结构和构建信息颗粒的事实标准。基于模糊集和粗糙集的聚类分析可在缺乏先验知识的前提下对含有不确定信息的数据进行初步分析。
1.1.1 模糊粗糙C均值算法文献[10]融合两种软计算方法,引入粗糙集理论中上下近似的概念和模糊集理论中模糊隶属度的概念,将归属关系模糊的数据样本划入类簇的边界区域,将归属关系明确的数据样本划入类簇的下近似区域,进而提出模糊粗糙C均值(FRCM)算法。考虑到类簇边界区域的不确定性,该文作者认为每个数据样本对类簇与类簇中心的影响程度都不同,因此,使用取值在0到1之间的模糊隶属度进行计算,如式(1)所示:
| $ {u}_{ij}=\frac{1}{\sum\limits_{z=1}^{C}{\left(\frac{{d}_{ij}}{{d}_{zj}}\right)}^{\frac{2}{m-1}}} $ | (1) |
其中,
| $ {a}_{ij}=\left\{\begin{array}{l}1, {x}_{j}\in {\underline C _i}\\ {u}_{ij}, {x}_{j}\in ({\overline{C}}_{i}-{\underline C _i})\end{array}\right. $ | (2) |
文献[11]在针对复杂不确定问题建模时,研究模糊化系数
| $ {\beta }_{ij}={\underline u }_{ij}+\frac{{N}_{i}}{N}({\overline{u}}_{ij}-{\underline u }_{ij})\mathrm{ }, {x}_{j}\in {C}_{i} $ | (3) |
其中,
| $ {\underline u }_{ij}=\mathrm{m}\mathrm{i}\mathrm{n}\left({u}_{ij}\right({m}_{1})\mathrm{ }, {u}_{ij}({m}_{2}\left)\right) $ | (4) |
| $ {\overline{u}}_{ij}=\mathrm{m}\mathrm{a}\mathrm{x}\left({u}_{ij}\right({m}_{1})\mathrm{ }, {u}_{ij}({m}_{2}\left)\right) $ | (5) |
PEDRYCZ等人提出的可信粒度准则[6, 24]基于提供的实验证据形成有意义的信息颗粒,被作为一种有效的数据粒化手段。依据数据本身的特性,可信粒度准则兼顾了粒子形成过程中的覆盖度与独特性,同时包含了优化的目标函数。
基于可信粒度准则,类簇

|
Download:
|
| 图 1 模糊粒子区间 Fig. 1 Interval of fuzzy granule | |
对所有数据样本按权重大小进行升序排列,得到新簇
| $ c\left(X\text{'}\right)={x}_{k}^{\mathrm{\text{'}}}, k=\underset{i}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}({u}_{1}^{\mathrm{\text{'}}}, {u}_{2}^{\mathrm{\text{'}}}, \cdots , {u}_{M}^{\mathrm{\text{'}}}) $ | (6) |
定义1 粒子的覆盖度[24]表示粒子的颗粒大小,其揭示了粒子具有的合理证据。在模糊划分过程中,一定范围内粒子区间越大,包含的数据样本越多,越有利于提取合理可信的粒子语义。描述覆盖度的粒化函数
| $ {C}_{\mathrm{C}\mathrm{o}\mathrm{v}}\left(\varOmega \right)=g\left(\right|b-a\left|\right)=\sum\limits_{j:a\le {x}_{j}\le b}{u}_{{x}_{j}} $ | (7) |
定义2 粒子的独特性[24]与粒子语义有关,可揭示粒子所含信息的抽象程度。在模糊划分过程中,一定范围内粒子区间越小,包含的数据样本越少,越有利于提取清晰的粒子语义。独特性粒化函数
| $ {S}_{\mathrm{S}\mathrm{p}\mathrm{e}}\left(\varOmega \right)=f\left(\right|b-a\left|\right)={\mathrm{e}}^{-|b-a|} $ | (8) |
定义3 目标函数反映粒子的整体质量。由于粒子的两大特性是相互冲突的,因此把代表粒子覆盖度和独特性的粒化函数组合为复合公式,并利用
| $ Q\left(\varOmega \right)=\underset{a, c, b}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{a}\mathrm{x}}g\left(\right|b-a\left|\right)\times f\left(\right|b-a\left|\right) $ | (9) |
对于类簇边界交叉重叠的数据集,类簇间规模的不均衡性对聚类分析的结果影响较大。当两个类簇的规模相差较大时,小规模类簇更容易受到边界区域的影响,且聚类中心点更易向规模较大的类簇偏移[14]。不同于传统的模糊隶属度量,区间二型模糊集合理论的隶属度在描述不均衡类簇边界交叉的不确定信息时具有明显的优势,IT2FCM算法也被用于不均衡类簇数据的聚类分析[12-14]。IT2FCM算法虽然一定程度上体现了不同区域数据样本的分布差异,但一些明确属于某个类簇的数据样本仍然需要参与其他类簇的隶属度量计算,未对具有不同归属程度的数据样本进行有区别的处理,会影响不均衡类簇数据聚类分析精度的提升,同时也会增加计算复杂度。
为削弱类簇规模不均衡问题的不利影响,本文在IT2FCM算法的基础上,引入粗糙集理论中上下近似的概念,考虑到不同区域的数据样本对类簇聚类的贡献度有明显差异以及计算所有数据样本模糊隶属度的时间成本,只对边界区域的数据样本进行二型区间模糊度量,而下近似区域数据样本取固定隶属度1,从而得到适用于多类簇交叉且分布不均衡数据的IT2FRCM算法,将其作为粒化第一阶段的聚类分析方法。
在IT2FRCM算法中,模糊隶属度计算公式[14]如下:
| $ {h}_{ij}=\left\{\begin{array}{l}1, {x}_{j}\in {\underline C _i}\\ {\underline u }_{ij}+\frac{{N}_{i}}{N}({\overline{u}}_{ij}-{\underline u }_{ij})\mathrm{ }, {x}_{j}\in ({\overline{C}}_{i}-{\underline C _i})\end{array}\right. $ | (10) |
相应的类簇中心迭代计算公式为:
| $ {v}_{i}=\frac{\sum\limits_{j=1}^{N}{h}_{ij}^{m}{x}_{j}}{\sum\limits_{j=1}^{N}{h}_{ij}^{m}}, {x}_{j}\in {C}_{i}, i=\mathrm{1, 2}, \cdots , C $ | (11) |
IT2FRCM算法在计算数据样本的权重时综合考虑了类簇的规模与空间分布信息,按规模大小自适应获得相对的加权系数,有效削弱了边界区域对聚类的影响,可避免类簇中心向边界区域严重偏移。
2.2 粒子特性描述问题基于IT2FRCM聚类所形成的基础信息粒,在描述粒子成粒依据时,保留数据样本与类簇归属关系的模糊隶属度,以区间范围内数据样本的权重和来度量粒子覆盖度[24]。传统的粒化算法对于粒子独特性的度量多基于余弦函数[14]、指数函数[15-17]和线性函数[18-20]等衰减函数,其将粒子区间大小看作是影响粒子独特性的唯一因素。然而,由图 2所示基础信息粒的区间划分图可知,在以类簇形式存在的基础信息粒中,数据样本(以*表示)的分布并不均匀:越靠近类簇中心(以+表示),分布的数据样本越密集;越靠近类簇边界,分布的数据样本越稀疏。当粒子区间长度(以→表示)均匀增加时,划入粒子区间内数据样本的个数往往会受到类簇中数据样本分布的影响而不均匀增加,从而导致粒子的独特性也发生不均衡变化。
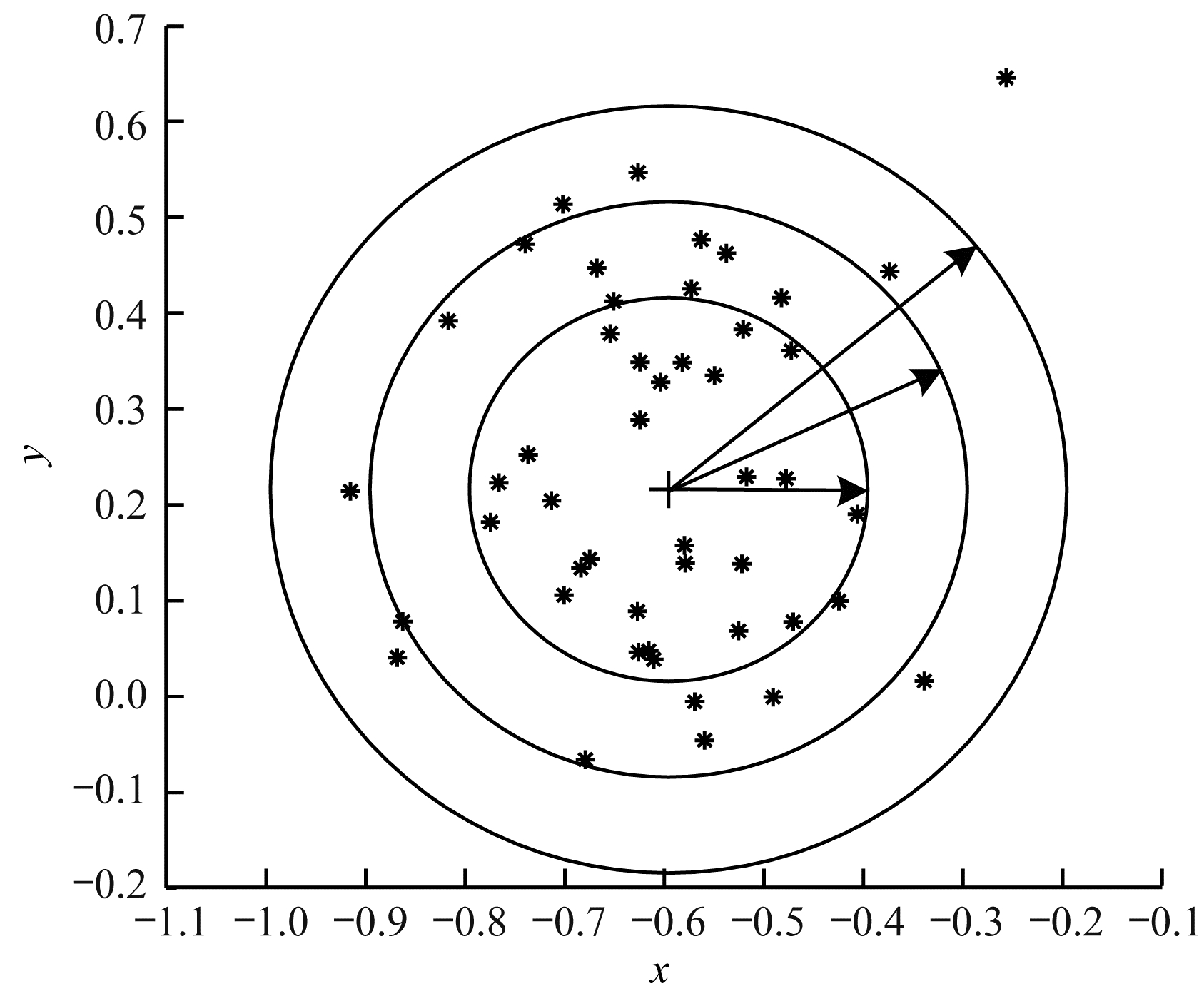
|
Download:
|
| 图 2 基础信息粒的区间划分图 Fig. 2 Interval partition graph of basic information granule | |
由此可知,粒子的独特性不仅与区间大小有关,而且还受到数据样本空间分布的影响。虽然传统描述粒子独特性的衰减函数一定程度上满足了随粒子区间增大粒子独特性减小的成粒原理,但简单的区间数值忽视了粒子内部数据样本的空间分布与疏密程度等因素对粒子特性的影响,不能很好地概括粒子内部的结构与性质。因此,区别于参数版可信粒度准则关于粒子独特性的度量方式,本文综合考虑区间与密度两大因素,重新设计描述独特性的指数函数,将粒子独特性的表达式改进为:
| $ f\left(\right|{x}_{j}-c\left|\right)={\mathrm{e}}^{-\frac{\sum\limits_{s=1}^{L|{x}_{j}-c|}|{x}_{s}-c(X\text{'}\left)\right|}{L|{x}_{j}-c|}\times |{x}_{j}-c|} $ | (12) |
其中,指数的分子表示粒子某区间范围内所有数据样本到均值中心c的距离和,分母表示
为解决分布不均衡数据的信息粒化问题,本文基于IT2FRCM聚类算法,以类簇的形式表示基础信息粒,并通过改进参数版可信粒度准则下描述粒子独特性的粒化函数,提出结合IT2FRCM与混合度量的两阶段信息粒化算法MMIG-IT2FRCM,算法流程如图 3所示。

|
Download:
|
| 图 3 MMIG-IT2FRCM算法流程 Fig. 3 Procedure of MMIG-IT2FRCM algorithm | |
算法的具体执行步骤如下:
算法 MMIG-IT2FRCM
输入 数据集
输出
第一阶段 执行IT2FRCM聚类算法。
步骤1 设置并初始化相关参数,随机选取类簇中心,设置相对距离阈值ep、最大迭代次数Iter和模糊化系数
步骤2 根据每个数据样本
步骤3 依据式(10)计算所有边界区域数据样本与所属类簇的模糊隶属度
步骤4 依据式(11)更新每个类簇的中心
步骤5 若各类簇中心不再发生变化或已经达到设定的最大迭代次数,算法终止,否则返回步骤2重新进行迭代计算。
第二阶段 基于IT2FRCM聚类结果进行信息粒化。
步骤1 初始化粒化抑制参数
步骤2 将类簇中心
步骤3 将每个参与粒化的数据样本
步骤4 依据式(9)选取粒子左边区域、右边区域中粒子覆盖度和独特性乘积最大的样本点,得出该维度下的粒子边界。
步骤5 确定信息粒子在各维空间下的左右边界后,输出信息粒子。
2.4 算法时间复杂度分析MMIG-IT2FRCM算法在第一阶段IT2FRCM聚类时,其时间复杂度由距离矩阵计算的时间复杂度
相较于传统参数版可信粒度准则下基于指数函数、线性函数或余弦函数粒化算法的时间复杂度
为验证MMIG-IT2FRCM算法的有效性,选取人工数据集和多组UCI标准数据集进行实验。首先对比分析IT2FRCM和FRCM聚类,然后对基于这两种聚类的4个粒化算法进行对比实验,验证本文MMIG-IT2FRCM粒化算法的性能优势。实验环境如下:CPU为Intel® CoreTM i5-4210H,内存为8 GB,操作系统为Windows10。
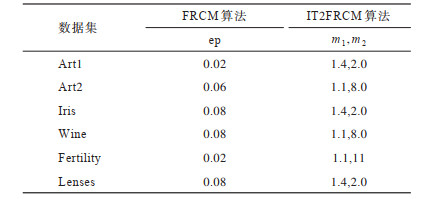
3.1 信息粒化两阶段数据初始化为保证实验的公平性,使用随机算法确定各数据集的初始聚类中心,同一数据集下所有聚类算法采用相同的初始聚类中心。相对距离阈值
|
下载CSV 表 1 不同数据集下2种聚类算法的参数设置 Table 1 Parameters setting of two clustering algorithms on different datasets |
按照正态分布随机生成3个分别包含25个、31个和20个数据样本的类簇作为人工数据集1 (Art1),按照正态分布随机生成3个分别包含30个、60个和100个数据样本的类簇作为人工数据集2 (Art2)。为明显区别于人工数据集1,通过控制正态分布的参数方差,使得人工数据集2的类簇区域重叠情况更严重,类簇规模不均衡的特征也更明显。Art2数据集下FRCM和IT2FRCM算法的聚类效果如图 4所示,其中,加粗且形状较大的几何图形表示对应类簇的中心,星形表示对应类簇误划分到其他类簇的数据样本。分析图 4中不同规模且重叠情况不同的3个类簇的聚类结果可知,采用IT2FRCM聚类算法得到的聚类中心更为理想。

|
Download:
|
| 图 4 Art2数据集下2种聚类算法的聚类效果 Fig. 4 Clustering effects of two clustering algorithms on Art2 database | |
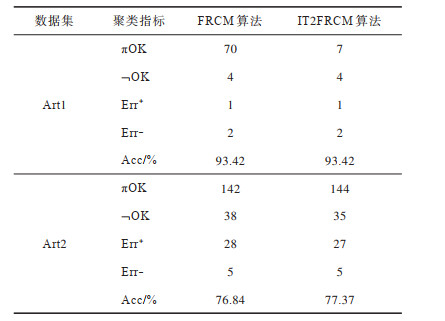
对2种聚类算法的聚类指标进行对比,如表 2所示。其中:
|
下载CSV 表 2 人工数据集下2种聚类算法的聚类指标 Table 2 Clustering indicators of two clustering algorithms on artificial datasets |
在第二阶段,对基于IT2FRCM算法的聚类结果实现信息粒化。实验中,分别以线性函数(LIN)、余弦函数(COS)、指数函数(EXP)和本文所提出的混合度量函数(MMIG)作为不同的独特性粒化函数,从而形成LIN-IT2FRCM、COS-IT2FRCM、EXP-IT2FRCM和MMIG-IT2FRCM这4种粒化算法进行对比实验。图 5为Art2数据集上4种粒化算法所得到的粒化结果。其中,黑色矩形框是由粒子左、右边界点形成的二维区间。黑色矩形框越大,表明粒子颗粒越大,越难提取有效的粒子语义,同时也表明粒子内部的数据样本越多,包含的证据越充分、合理。由图 5可知,本文提出的MMIG-IT2FRCM粒化算法所形成的粒子区间相较于其他3种粒化算法覆盖了更多的数据样本,其形成的粒子区间包含了更为充分的实验证据。

|
Download:
|
| 图 5 Art2数据集下4种粒化算法的粒化效果 Fig. 5 Granularity effects of four granulation algorithms on Art2 database | |
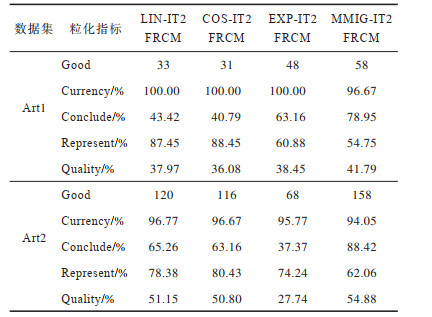
在规模不均衡、空间分布明显不同的2个人工数据集下对4种粒化算法的粒化指标进行对比,如表 3所示,其中:Good为归类正确数,即聚类正确的样本个数;Currency为归类正确率,表示粒子内部所有数据样本中归类正确的数据样本所占的比例;Conclude为覆盖率,表示粒子覆盖范围;Represent为独特性指标,反映粒子群的代表性;Quality反映生成粒子的质量,是粒子群整体质量的最终评判标准。分析表 3中各项粒化指标可知,MMIG-IT2FRCM粒化算法在粒子聚类正确数、粒子整体质量和粒子的覆盖度与独特性等重要指标上均取得了最佳值。相较于其他3种粒化算法,该算法具有明显的性能优势,得到的粒子群整体质量更好。
|
下载CSV 表 3 人工数据集下4种粒化算法的粒化指标 Table 3 Granulation indicators of four granulation algorithms on artificial datasets |
选取4个标准的UCI数据集Lenses、Wine、Iris、Fertility进行实验分析。小数据集Lenses的3个类簇各有4个、5个和15个数据样本。Wine数据集的3个类簇各有59个、78个、41个数据样本。Iris数据集的3个类簇各有50个样本。Fertility数据集的2个类簇各有88个和12个数据样本。数据集Iris、Wine数据样本分布均匀,Lenses数据样本几乎不交叉。3个数据集体现了不同的类簇交叉重叠程度,即
4个UCI标准数据集在2种聚类算法下的实验结果如表 4所示。其中:OK为位于类簇下近似区域且聚类正确的样本数;Bd为边界区域的样本个数;Iter为算法的迭代次数;AverTime为平均时间。从表 4可以看出,除规模一致、均匀分布的Iris数据集外,其他规模差异大且非均匀分布的数据集耗费在IT2FRCM聚类算法中的时间复杂度远低于FRCM聚类算法。在对类簇规模差异大且样本点分散的Fertility数据集聚类时,IT2FRCM算法只迭代了4次就快速收敛,而FRCM算法达到迭代次数上限后,被迫停止算法,时间复杂度很高。因此,综合对比聚类正确数、迭代次数和平均时间等聚类指标可知,对于多类簇交叉且数据不均衡分布的数据集,IT2FRCM算法在迭代运行过程中能够实现快速收敛和准确分类。
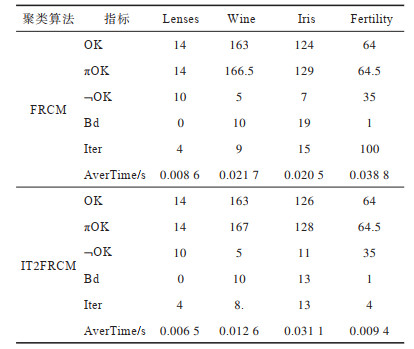
|
下载CSV 表 4 UCI数据集下2种聚类算法的聚类指标对比 Table 4 Clustering indicators of two clustering algorithms on UCI datasets |
4个UCI标准数据集下4种粒化算法的实验结果如表 5所示。可以看出,MMIG-IT2FRCM粒化算法在归类正确数、粒子覆盖度和独特性指标上均取得了最佳值。分别对比4个UCI数据集下4种粒化算法的归类正确数可知,本文提出的MMIG-IT2FRCM粒化算法生成的信息粒子内部聚类正确的数据样本数更多,提取的粒子信息可用性强。分析粒子两大特性可知,MMIG-IT2FRCM粒化算法在Lenses、Wine、Iris、Fertility数据集上覆盖度取值明显高于相同数据集下其他3种粒化算法中覆盖度的最佳值,可见MMIG-IT2FRCM粒化算法生成的信息粒粒子区间更大。同时,MMIG-IT2FRCM粒化算法在4个标准数据集下独特性取值明显低于相同数据集下其他3种粒化算法中的最佳值,反映了基于该粒化算法的粒子结构更为紧凑,更利于提取清晰的粒子语义。随着粒子区间范围扩大,会有更多边界区域的误分样本被划入粒子区间,因此,MMIG-IT2FRCM粒化算法在Wine、Iris、Fertility数据集上的归类正确率略微逊色于其他3种粒化算法,但粒子覆盖度和独特性两大特性指标得到明显提升,与经典的EXP-IT2FRCM粒化算法相比,其正确率的取值仍然控制在合理的范围。关于粒子的整体质量,对比4种粒化算法的取值情况可知,MMIG-IT2FRCM粒化算法在Lenses和Iris数据集下均取得了最佳值,在Wine和Fertility数据集下与其他3种粒化算法的取值情况相近。
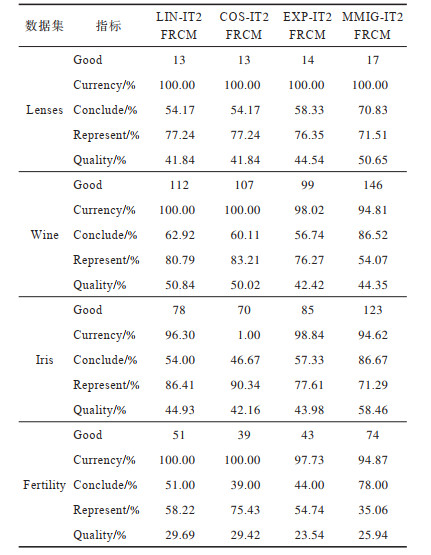
|
下载CSV 表 5 UCI数据集下4种粒化算法的粒化指标 Table 5 Granulation indicators of four granulation algorithms on UCI datasets |
综合4个数据集类簇的交叉情况(
考虑反映粒子本质的核心指标,在类簇规模一致、数据分布均匀且边界区域轻微交叉的Iris数据集与类簇规模差别大、类簇重叠严重的Fertility数据集下做进一步对比,4种粒化算法的实验结果如图 6所示。可以看出,本文提出的MMIG_IT2FRCM粒化算法相较其他粒化方法,在反映生成粒子性质与质量的核心指标上均取得理想表现,对类簇规模不均衡且边界区域交叉重叠的数据集具有更强的适用性。

|
Download:
|
| 图 6 Iris和Fertility数据集下的粒化指标 Fig. 6 Granulation indicators on Iris dataset and Fertility dataset | |
综合2组人工数据集和4组UCI标准数据集的实验结果可知,本文提出的MMIG-IT2FRCM粒化算法最终划分形成的可信信息粒子具有更清晰的粒子语义,并最大化满足粒度层次上实验证据合理的成粒原理。
4 结束语针对数据分布不均衡且多类簇交叉数据集的信息粒化问题,本文提出一种结合区间二型FRCM与混合度量的两阶段信息粒化算法。基于快速收敛的IT2FRCM聚类算法为粒化提供基本信息粒,同时考虑密度和区间的共同作用,改进粒子独特性描述函数。在多组人工数据集和UCI标准数据集下的实验结果表明,本文算法在粒子两大特性的多个指标上均取得了较为理想的结果,所得信息粒结构紧凑并具有代表性。针对不同分布且不同规模大小的数据集,下一步将自适应调整信息粒的粒度大小以实现不同层次的信息粒化,同时提高算法的适应性。
| [1] |
WANG Guoyin, ZHANG Qinghua, HU Jun. An overview of granular computing[J]. CAAI Transactions on Intelligent Systems, 2007, 12(6): 8-26. (in Chinese) 王国胤, 张清华, 胡军. 粒计算研究综述[J]. 智能系统学报, 2007, 12(6): 8-26. |
| [2] |
MIAO Duoqian, WANG Guoyin, LIU Qing. Granular computing: past, present and future[M]. Beijing: Science Press, 2007. (in Chinese) 苗夺谦, 王国胤, 刘清. 粒计算: 过去、现在与展望[M]. 北京: 科学出版社, 2007. |
| [3] |
ZHANG Fengwang. Application of SVM based on infor-mation granulation in securities time series analysis[D]. Kunming: Kunming University of Science and Technology, 2014. (in Chinese) 张丰旺. 基于信息粒化的SVM在证券时间序列分析中的应用[D]. 昆明: 昆明理工大学, 2014. |
| [4] |
PEDRYCZ W, AL-HMOUZ R, MORFEQ A, et al. The design of free structure granular mappings: the use of the principle of justifiable granularity[J]. IEEE Transactions on Cybernetics, 2013, 43(6): 2105-2113. DOI:10.1109/TCYB.2013.2240384 |
| [5] |
ZHU X, PEDRYCZ W, LI Z. Granular description of data: building information granules with the aid of the principle of justifiable granularity[C]//Proceedings of 2016 IEEE International Conference on Fuzzy Systems. Washington D.C., USA: IEEE Press, 2016: 969-976.
|
| [6] |
AL-HMOUZ R, PEDRYCZ W, BALAMASH A, et al. From data to granular data and granular classifiers[C]//Proceedings of 2014 IEEE International Conference on Fuzzy Systems. Washington D.C., USA: IEEE Press, 2014: 432-438.
|
| [7] |
GACEK A, PEDRYCZ W. Clustering granular data and their characterization with information granules of higher type[J]. IEEE Transactions on Fuzzy Systems, 2015, 23(4): 850-860. DOI:10.1109/TFUZZ.2014.2329707 |
| [8] |
EFFATI S, SADOGHI H, YAZDI A J. Fuzzy clustering algorithm for fuzzy data based on α-cuts[M]. [S. l. ]: IOS Press, 2013.
|
| [9] |
PETER G, LINGRAS P. Rough sets: selected methods and applications in management and engineering[M]. Berlin, Germany: Springer, 2012.
|
| [10] |
HU Qinghua, YU Daren. An improved clustering algorithm for information granulation[C]//Proceedings of International Conference on Fuzzy Systems and Knowledge Discovery. Berlin, Germany: Springer, 2005: 494-504.
|
| [11] |
HWANG C, RHEE C H. Uncertain fuzzy clustering: interval type-2 fuzzy approach to C-Means[J]. IEEE Transactions on Fuzzy Systems, 2007, 15(1): 107-120. DOI:10.1109/TFUZZ.2006.889763 |
| [12] |
YU Long, XIAO Jian, ZHOU Cong. Robust interval type-2 possibilistic C-Means clustering[J]. Control and Decision, 2009, 24(4): 503-507. |
| [13] |
RUBIO E, CASTILLO O, MELIN P. Interval type-2 fuzzy system design based on the interval type-2 fuzzy C-Means algorithm[M]//COLLAN M, FEDRIZZI M, KACPRZYK J. Fuzzy technology. Berlin, Germany: Springer, 2016.
|
| [14] |
LU Ruiqiang. Rough clustering and granulation analysis for uncertain information and its application[D]. Nanjing: Nanjing University of Finance & Economics, 2018. (in Chinese) 逯瑞强. 不确定信息的粗糙聚类与粒化分析及应用[D]. 南京: 南京财经大学, 2018. |
| [15] |
PEDRYCZ W. The principle of justifiable granularity and an optimization of information granularity allocation as fundamentals of granular computing[J]. Journal of Information Processing Systems, 2011, 7(3): 397-412. DOI:10.3745/JIPS.2011.7.3.397 |
| [16] |
PEDRYCZ W, SUCCI G, SILLITTI A, et al. Data description: a general framework of information granules[J]. Knowledge-Based Systems, 2015, 80: 98-108. DOI:10.1016/j.knosys.2014.12.030 |
| [17] |
ZHONG C, PEDRYCZ W, WANG D, et al. Granular data imputation: a framework of granular computing[J]. Applied Soft Computing, 2016, 46: 307-316. DOI:10.1016/j.asoc.2016.05.006 |
| [18] |
WANG D, PEDRYCZ W, LI Z. Design of granular interval-valued information granules with the use of the principle of justifiable granularity and their applications to system modeling of higher type[J]. Soft Computing, 2016, 20(6): 2119-2134. DOI:10.1007/s00500-015-1904-1 |
| [19] |
SHEN Y, PEDRYCZ W, WANG X. Clustering homogeneous granular data: formation and evaluation[J]. IEEE Transactions on Cybernetics, 2019, 49(4): 1391-1402. DOI:10.1109/TCYB.2018.2802453 |
| [20] |
WANG D, PEDRYCZ W, LI Z. Granular data aggregation: an adaptive principle of the justifiable granularity approach[J]. IEEE Transactions on Cybernetics, 2018, 49(2): 1-10. |
| [21] |
PEDRYCZ W, WANG X. Designing fuzzy sets with the use of the parametric principle of justifiable granularity[J]. IEEE Transactions on Fuzzy Systems, 2016, 24(2): 489-496. DOI:10.1109/TFUZZ.2015.2453393 |
| [22] |
LIU S, PEDRYCZ W, GACEK A, et al. A two-phase method of forming a granular representation of signals[J]. Signal Processing, 2017, 141: 1-15. DOI:10.1016/j.sigpro.2017.05.026 |
| [23] |
WANG X, PEDRYCZ W, GACEK A, et al. From numeric data to information granules: a design through clustering and the principle of justifiable granularity[J]. Knowledge-Based Systems, 2016, 101: 100-113. DOI:10.1016/j.knosys.2016.03.012 |
| [24] |
FU C, LU W, PEDRYCZ W, et al. Fuzzy granular classifica-tion based on the principle of justifiable granularity[J]. Knowledge-Based Systems, 2019, 170: 89-101. DOI:10.1016/j.knosys.2019.02.001 |
| [25] |
PEDRYCZ W, HOMENDA W. Building the fundamentals of granular computing: a principle of justifiable granularity[J]. Applied Soft Computing, 2013, 13(10): 4209-4218. DOI:10.1016/j.asoc.2013.06.017 |
 2021, Vol. 47
2021, Vol. 47

