近年来, 随着无线传感器网络及物联网通信等移动互联技术的不断进步, 基于位置的社交网络服务得到了迅速发展, 如Foursquare、Gowalla等。用户可以用签到的形式记录他们所到地点的地理标签信息和物理位置, 这种行为被称为“用户签到”行为[1]。基于位置的社交网络的个性化推荐正是利用这些用户签到信息, 帮助用户探索新的区域与发现新的兴趣点, 促进广告商对目标用户推送相应的广告, 从而使基于位置的社交网络更具有吸引力。
相对于传统的推荐问题, 地点推荐面临数据稀疏问题并受到地理位置影响。在基于位置的社交网络中, 地点的数量规模巨大, 而每个用户访问的地点却很有限, 这导致用户-地点的签到矩阵是高稀疏矩阵[2]。并且用户的活动通常限制在一个范围内, 他们经常会访问在活动区域附近的地点(如家或工作地点附近)[3]。而以往的基于领域的协同过滤算法通过签到2个地点的共同用户来计算地点的相似性, 其结果会受到热门地点的影响, 在此基础上计算用户相似性时也会受到热门地点的影响。
本文提出一种基于地点转换向量(Location2vec)的地点推荐方法, 通过获取用户的时间签到序列, 剔除冷门地点, 采用连续词袋(Continuous Bag-of-Words, CBOW)模型以及负采样的训练方法将地点转换成向量, 根据向量的余弦相似性计算地点之间的相似性, 进而获得用户对地点的偏好程度, 同时计算签到冷门地点的用户之间的相似性, 构建用户-地点的偏好矩阵, 最终结合地点位置的访问概率得到用户对未签到地点的评分, 填补用户-地点签到矩阵, 并生成用户推荐列表。
1 相关工作在推荐系统中, 目前使用最广泛的是协同过滤技术。在地点推荐中, 用户的签到数据存在着高稀疏问题, 导致传统计算地点相似性与用户相似性的方法的可靠性降低, 推荐效果有待提高。文献[4]结合修正公式改进Jaccard公式计算签到用户的相似性系数, 同时还考虑评分的共同项及差异项对用户相似度的影响。文献[5]提出一种提取用户签到序列特征的方法。文献[3]在计算好友之间的相似性时考虑了用户的社交网络关系以及地理距离, 但未考虑用户活动的偏好信息。文献[6]从用户偏好信息以及地点标签的相似度对用户进行推荐。文献[7]提出一种基于熵的用户相似性度量方法。该方法考虑了用户评分的相对误差, 提高了邻近用户的搜索质量, 但没有考虑地理位置因素对用户签到行为的影响。文献[8]认为地理距离的远近与用户的签到概率存在着长尾分布的关系, 利用朴素贝叶斯法对用户进行地点推荐。文献[9]认为用户的访问行为通常包含几个中心地点, 因此利用高斯模型模拟用户的偏好, 进行地点推荐。但文献[8-9]仅从地理位置的角度出发进行推荐, 未考虑到用户之间的互动对签到行为的影响。
传统的地点相似性计算方法采用的数据是签到2个地点的共同用户的数量, 当计算新地点与其他地点相似性时, 得到的结果可能偏低。例如, 某地有一个餐厅A与公园B, 该地用户经常签到完A地点后会在B地点签到, 而这时新建一个公园C, 刚开始可能部分人签到完A去公园C签到, 上述方法计算出的公园C与公园B、餐厅A的相似性很低, 但事实上公园C与公园B、餐厅A具有较高的相似性。而且传统的地点相似性计算方法会受到热门地点的影响, 导致热门地点与其他地点都有着一定程度的相似性。为此, 本文提出一种Location2vec方法, 考虑用户时间签到序列, 将地点转换成向量后计算其余弦相似性, 进而获得用户偏好。
2 结合冷门地点和Location2vec的推荐框架 2.1 总体思路本文首先获取用户的时间签到序列, 将出现频次小于6的地点视为冷门地点, 剔除签到数据集。通过Location2vec算法将非冷门地点转换为长度统一的地点向量, 计算地点之间的余弦相似度, 进而计算用户对非冷门地点的偏好程度。同时对于冷门地点集合, 本文通过计算签到冷门地点的用户相似性进而计算用户对冷门地点的偏好。结合用户的活跃中心与未访问地点的距离计算用户访问该地点的概率得到用户对该地点的评分, 最终生成对用户的推荐列表。图 1为本文的推荐框架。

|
Download:
|
| 图 1 基于Location2vec的地点推荐框架 | |
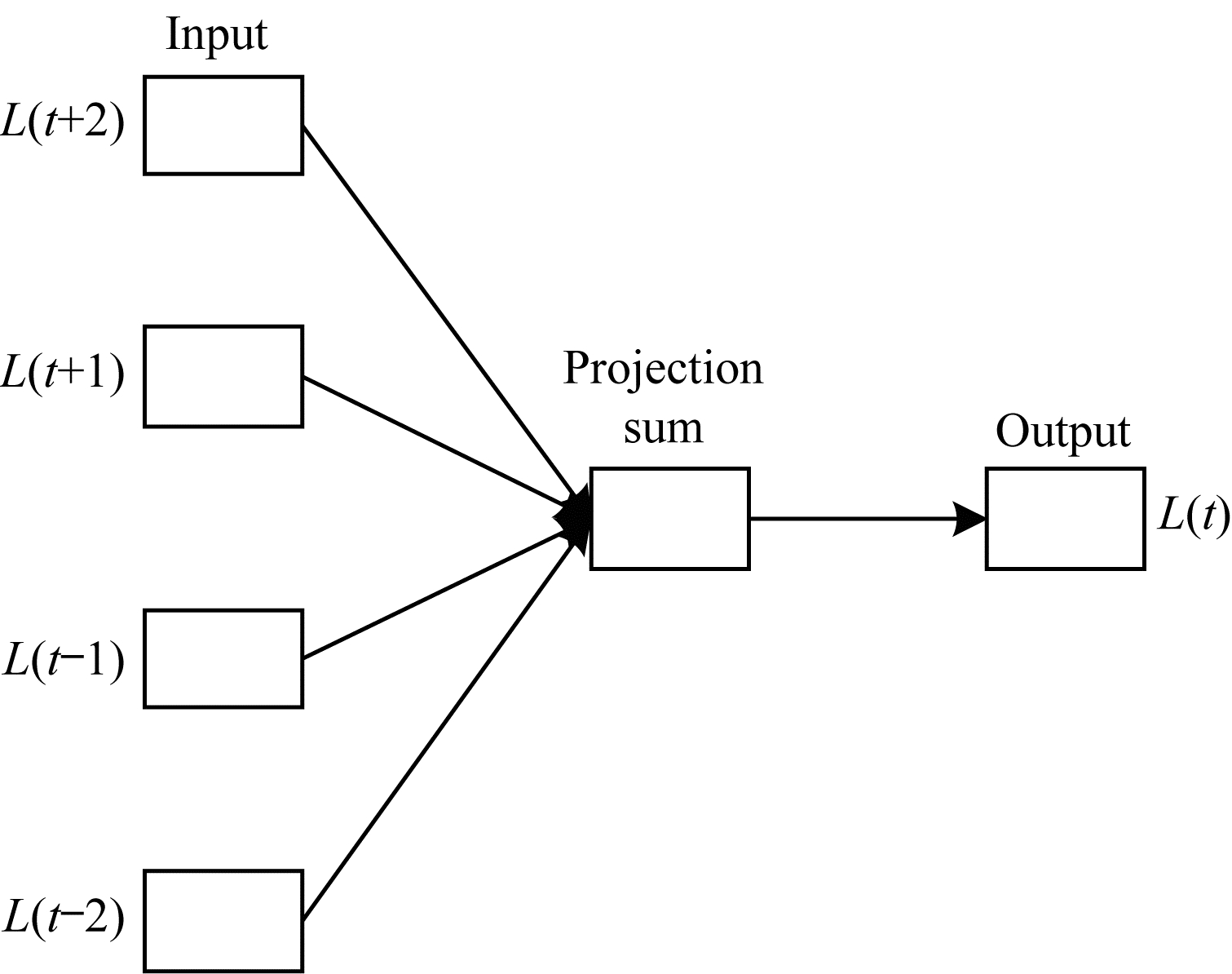
本文采用Location2vec算法是为了获得用户时间签到序列的潜在特征, 同时该模型不会受到新地点的影响, 并且在训练过程中, 对高频地点降采样降低了热门地点对地点相似性计算的影响。本文的Location2vec算法基于文献[10]提出的CBOW模型, 是通过签到序列前后的地点来预测当前地点出现概率的模型, 如图 2所示, 其目标函数为:
| $\sum\limits_{l \in C} {\lg } p(l|Contenxt(l))$ |
|
Download:
|
| 图 2 CBOW模型 | |
获取每个用户在测试集按时间先后的签到序列, 剔除出现次数小于n的地点, 得到每个用户的签到集合:
| $L = \left\{ {{L_{{u_1}}},{L_{{u_2}}}, \cdots ,{L_{{u_n}}}} \right\}$ |
为了提高训练速度并消除热门地点对地点之间相似度计算的影响, 本文采用负采样训练方法[11]。已知地点l签到时间前后的地点集合为Context(l), 在CBOW模型中, 对于给定的Context(l), 点l即为一个正样本, 其他地点为负样本NEG(l)。对于
| ${L_a} = \left\{ {\begin{array}{*{20}{l}} {1,\tilde l = l}\\ {0,\tilde l \ne l} \end{array}} \right.$ |
对于给定的正样本(Context(l), l), 目标函数为:
| $\max \prod\limits_{{l_i} \in \{ l\} \cup NEG(l)} p \left( {{l_i}|Context{\rm{ }}(l)} \right)$ |
本文负样本采集机理为权重采样, 即在用户签到集合中出现次数多的地点被选为负样本的概率会大, 其每个地点的样本采样率计算如下:
| $p\left( {{l_i}} \right) = \frac{{counter{{\left( {{l_i}} \right)}^{\frac{3}{4}}}}}{{\sum\limits_l {counter} {{(l)}^{\frac{3}{4}}}}}$ |
其中, 对词频取幂是一种平滑策略, 降低热门签到地点被选中的概率, 即降低了热门地点对地点向量训练的影响。
| $P\left( {{l_i}} \right) = 1 - \sqrt {\frac{t}{{f\left( {{l_i}} \right)}}} $ |
其中, P(li)为地点li被排除负样本的概率, f(li)为地点在用户签到集合的出现概率, t为常数, 本文取1×10-4。最后通过随机梯度上升的方法[10]求解得出各个地点之间的地点向量。Location2vec的伪代码如下:
输入 用户签到序列集合L
输出 地点向量 V
Location_size←get_Location_size(L)
V←初始化向量(Location_size, 50)
θ←初始化向量(Location_size, 50)
For all li∈L do
e←0
For all u={li}∪NEG(li) do
q←σ(XTliθu)
g←η(Lli(u)-q)
e←e+gθu
θu←θu+gXl
End for
For all u∈context(li) do
V(u)←V(u)+e
End for
End for
2个地点之间的余弦相似度计算公式如下:
| $\cos \left( {{\mathit{\boldsymbol{l}}_1},{\mathit{\boldsymbol{l}}_2}} \right) = \frac{{\sum\limits_{i = 1}^n {{x_i}} {y_i}}}{{\sqrt {\sum\limits_{i = 1}^n {x_i^2} } \sqrt {\sum\limits_{i = 1}^n {y_i^2} } }}$ |
其中, l1=[x1, x2, …, xn], l2=[y1, y2, …, yn]。
文献[12]提出将ItemCF的相似度矩阵按最大值归一化, 可以提高推荐的准确率, 即:
| ${w_{ij}} = \frac{{{w_{ij}}}}{{\mathop {\max }\limits_j {w_{ij}}}}$ |
则用户对该地点的偏好计算如下:
| $pre(u,l) = \sum\limits_{i \in N(u) \cap S(j,k)} {{w_{ji}}} {r_{ui}}$ |
其中, S(j, k)表示通过计算地点向量之间的余弦相似度得出来的与地点j最相似的k个地点, N(u)为用户u签到过的地点集合。wji表示地点j和地点i之间的余弦相似度按最大值归一化后相似度, rui表示用户u在地点i的签到次数。
2.3 签到冷门地点的用户相似性计算文献[13]指出2个用户对冷门物品采取同样的行为更能反映他们兴趣的相似度, 因此本文将训练集中地点签到频次小于n的地点作为冷门地点集合, 计算签到冷门地点的用户之间的相似性。
| ${w_{uv}} = \frac{{|N(u) \cap N(v)|}}{{\sqrt {\left| {N(u)} \right|\left| {N(v)} \right|} }}$ |
其中, N(u)和N(v)分别表示用户u、v签到冷门地点的集合。通过用户相似性计算用户对冷门地点的用户偏好:
| $pre(u,l) = \sum\limits_{v \in S(u,k) \cap N(I)} {{w_{uv}}} {r_{vl}}$ |
其中, S(u, k)表示通过签到冷门地点计算出来的与用户u最相似的k个用户, N(l)表示对地点l有过签到行为的用户集合, wuv表示用户u和用户v的用户相似性, rvl表示用户v对地点l的签到次数。
2.4 用户访问概率用户的签到地点主要围绕一个中心, 称之为用户的活跃中心, 其计算步骤为:
1) 获取用户的签到序列。
2) 计算用户在每个地点的签到次数占该用户总签到次数的比例。
3) 若某个地点的签到次数占该用户总签到次数的比例超过30%, 则将该地点视为用户的活跃中心。
4) 若该用户所有的签到地点占总体签到均未达到30%, 计算该用户所有签到地点的中心点, 具体公式见文献[14]。
文献[3]认为用户的签到概率随地点距离服从幂律分布, 即:
| $pro\left( {{l_r}|{l_u}} \right) = a \times dist{\left( {{l_r},{l_u}} \right)^b}$ |
其中, dist()代表距离函数, a和b是幂律分布的参数, 根据现有的参数进行估计。lr为用户为访问的地点, lu表示用户u的活跃中心。地球上2点之间的距离计算公式为:
| $\begin{array}{*{20}{l}} {dist\left( {{l_1}|{l_2}} \right) = 2R \times }\\ {\;\;\;\;\;\arcsin \left( {\sqrt {{{\sin }^2}\left( {\frac{{{\alpha _1} + {\alpha _2}}}{2}} \right) + \cos {\alpha _1}\cos {\alpha _2}{{\sin }^2}\left( {\frac{{{\lambda _1} + {\lambda _2}}}{2}} \right)} } \right)} \end{array}$ |
其中, R表示地球的半径, α1和α2表示地点l1和l2的纬度, λ1和λ2分别表示地点l1和l2的经度。
2.5 用户评分本文通过地点相似性和用户相似性分别计算用户的偏好, 进而计算用户u对未签到地点l的评分, 具体计算如下:
1) 地点l在冷门地点集合中,
| $rank(u,l) = pro\left( {l|{l_u}} \right) \cdot \sum\limits_{v \in S(u,k) \cap N(l)} {{w_{uv}}} {r_{vl}}$ |
其中, pro(l|lu)表示用户u对冷门地点l的访问概率。
2) 地点l不在冷门地点集合中,
| $rank(u,l) = pro\left( {{l_j}|{l_u}} \right) \cdot \sum\limits_{i \in N(u) \cap S(j,k)} {{w_{ji}}} {r_{ui}}$ |
其中, pro(lj|lu)表示用户u对地点lj的访问概率。
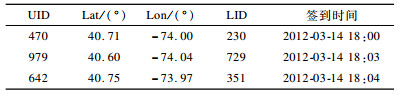
3 实验数据分析 3.1 实验数据集本文实验使用Foursquare数据集[15], 其包括1 083个用户对38 333个地点的227 427条签到数据。为了使实验更精确, 在数据集预处理阶段剔除了签到次数小于5的用户以及被签到次数小于5的地点, 最后得到的实验数据集包括用户签到数据92 056条, 总共有1 071个用户和5 291个地点。在数据集中随机抽取80%作为训练集, 剩下的20%作为测试集, 表 1为该数据集的签到示例, UID表示用户ID, LID表示地点ID。
|
下载CSV 表 1 Fousquare数据集签到数据示例 |
本文采用准确率(Precision)、召回率(Recall)评价推荐效果。由于精确率和召回率受推荐列表长度的影响, 推荐列表越长, 精确率越低, 召回率则越高, 因此本文同时引入了F1值作为评价指标。
| $Precision@N = \frac{{\sum\limits_{u \in U} {\left| {R(u) \cap T(u)} \right|} }}{{\sum\limits_{u \in U} {\left| {R(u)} \right|} }}$ |
| $Recall{\rm{@}}N = \frac{{\sum\limits_{u \in U} {\left| {R(u) \cap T(u)} \right|} }}{{\sum\limits_{u \in U} {\left| {T\left( u \right)} \right|} }}$ |
| $F1@N = \frac{{2 \cdot Precision@N \cdot Recall@N}}{{Precision@N + Recall@N}}$ |
其中, R(u)为推荐给用户u的地点列表, T(u)为测试集中用户u签到过的地点列表, N为推荐地点数量。
3.3 实验结果与分析为了验证算法的有效性, 本文对比5种算法:
1) 基于用户的协同过滤算法(UCF)。
2) 基于地点的协同过滤算法(LCF)。
3) 基于用户与地理位置访问概率的协同过滤算法(UG-CF)。
4) 基于Location2vec与地理位置访问概率的协同过滤算法(GL-CF)。
5) 基于Location2vec、冷门地点及访问概率的协同过滤算法(GLC-CF)。
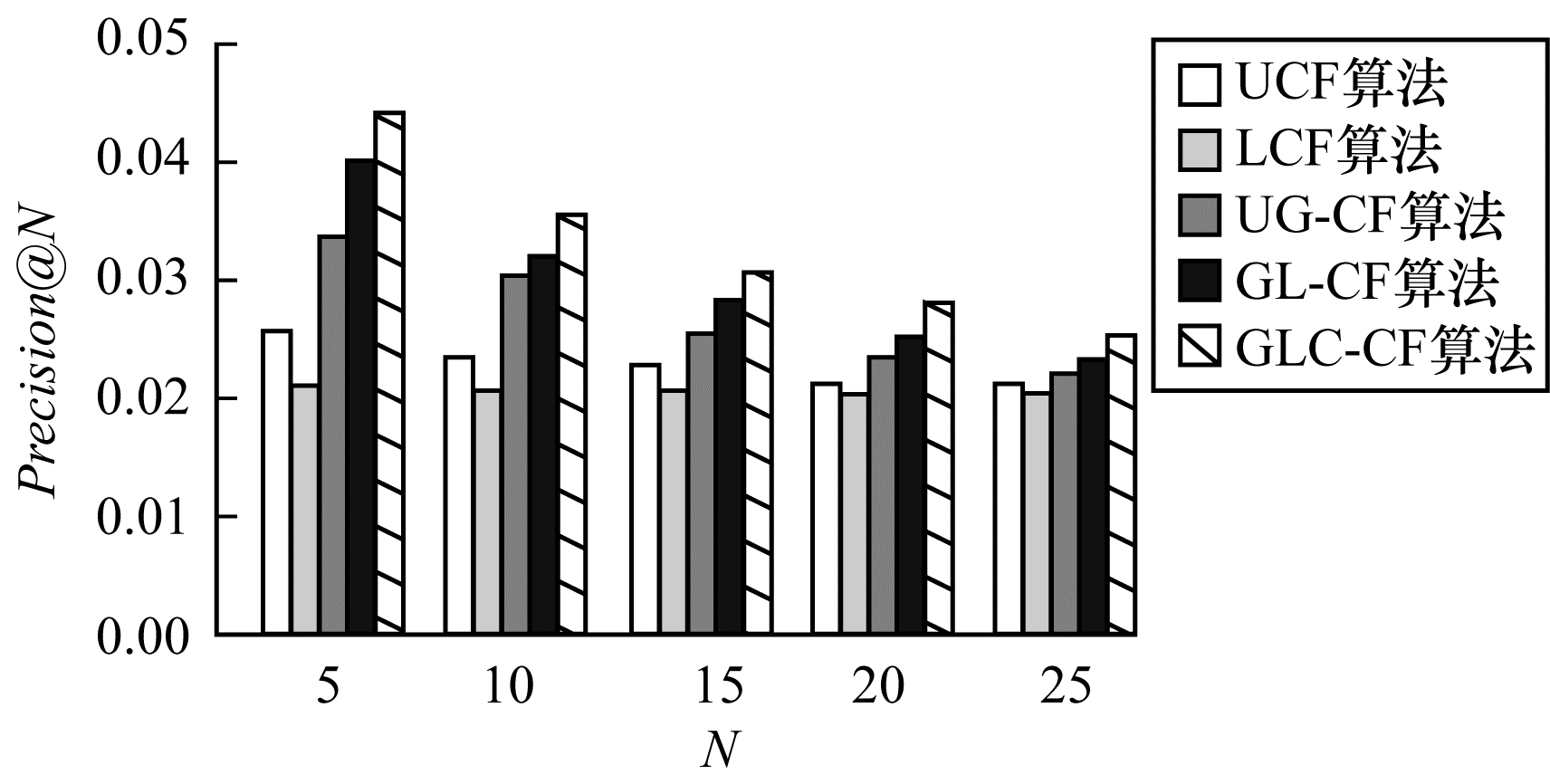
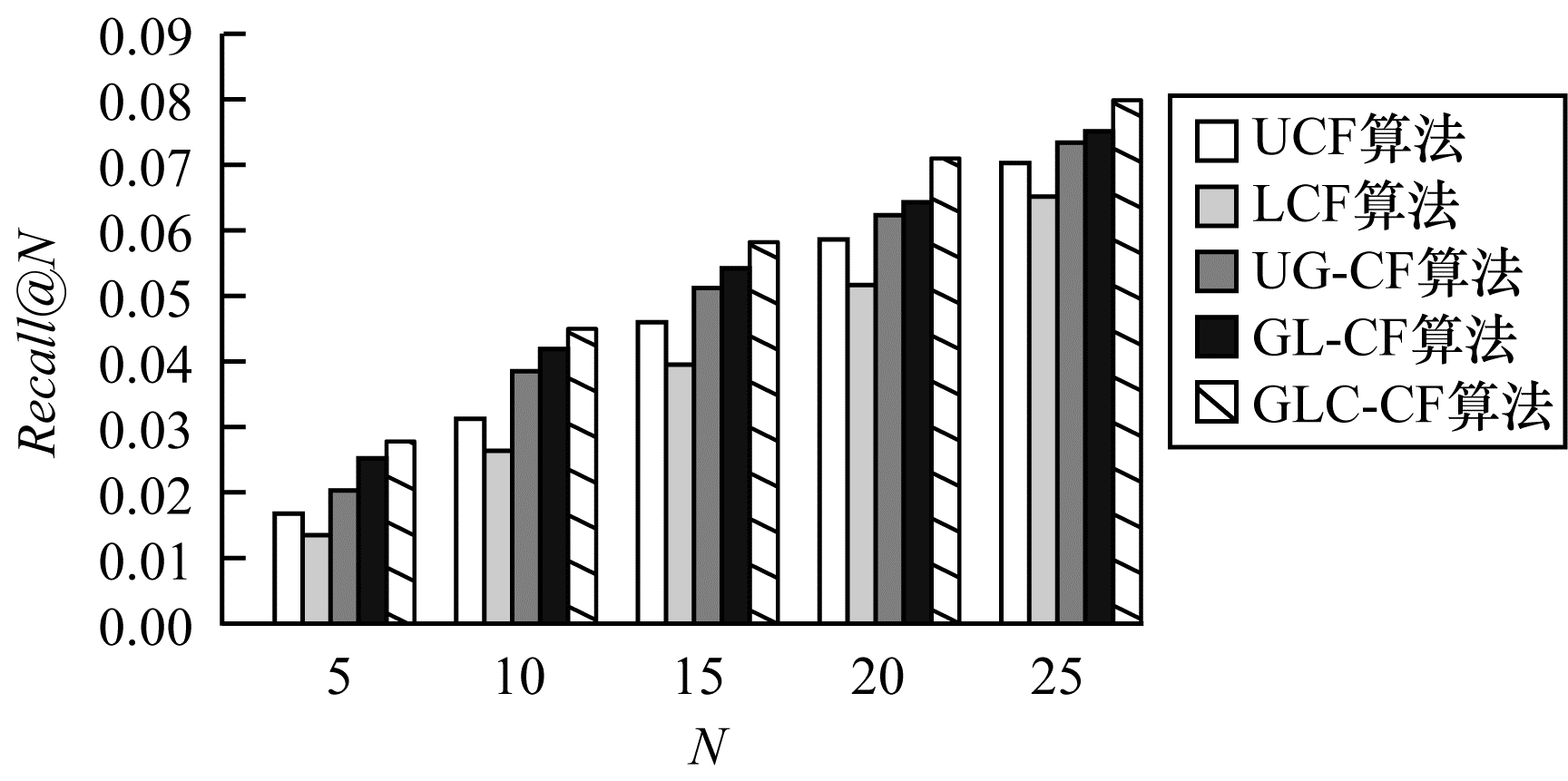
图 3~图 5分别为各个算法的准确率、召回率, F1值的大小比较, 从图中可以看到随着推荐列表N的长度不断上升, 各个推荐算法的准确率在不断降低, 召回率在不断上升。相对于传统的基于近邻的协同过滤算法UCF、LCF, UG-CF的推荐效果更优, 这表明考虑结合地理位置的影响比单纯考虑用户和地点之间的相似性的效果更优。而本文提出的GL-CF、GLC-CF相对于UCF、LCF、UG-CF的推荐效果更优, 这是因为GL-CF、GLC-CF不仅结合了地理位置因素的影响, 同时Location2vec方法能够学习用户签到序列的潜在特征, 更好地计算地点之间的相似性, 同时降低了热门地点对地点之间相似性计算的影响。而GLC-CF比GL-CF的推荐效果更优, 这是因为去除了冷门地点的影响, Location2vec训练出来的地点向量效果更好, 而同时通过冷门地点计算用户之间的相似性, 分别计算用户偏好, 使得推荐结果效果更优。
|
Download:
|
| 图 3 不同算法推荐准确率 | |
|
Download:
|
| 图 4 不同算法推荐召回率 | |

|
Download:
|
| 图 5 不同算法推荐F1值 | |
由图 5可知, 当N=15时, 本文算法的F1值最高, 为0.040, 而此时UCF、LCF、UG-CF、GL-CF算法F1值分别为0.003、0.027、0.034、0.036。
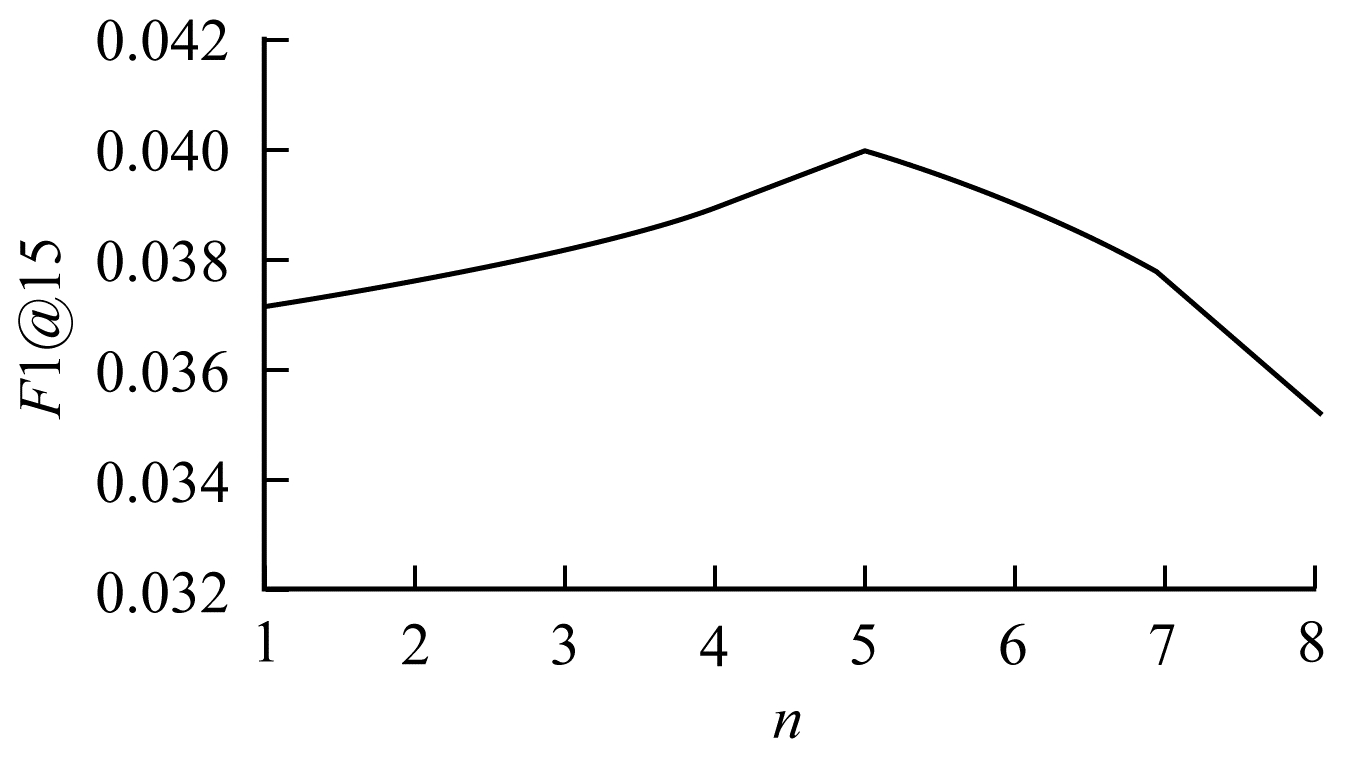
图 6为阈值n选取不同值时, 推荐列表长度固定为15, GLC-CF的F1值的变化曲线。可以看到在n取5时F1值的效果达到最高。当n取大于5的数时F1值逐渐降低。
|
Download:
|
| 图 6 参数n对推荐效果的影响 | |
通过以上对比实验, 可以看出本文提出的GLC-CF方法改进了用户相似性计算以及地点相似性计算, 相对于传统的推荐算法, 本文方法效果较好。
4 结束语本文提出了一种Location2vec算法, 将用户的签到地点划分为冷门地点和非冷门地点。对非冷门地点, 通过CBOW模型以及负采样的训练方法将地点转换成向量, 用向量的余弦相似性表示地点之间的相似性, 同时计算签到冷门地点的用户之间的相似性, 构建用户-地点的偏好矩阵, 结合地点位置的访问概率得到用户对未签到地点的评分, 将评分排在前N的地点推荐给用户。实验结果表明, 对比基于用户的协同过滤算法, 本文算法推荐效果更好。下一步将结合用户对地点的评论信息, 提高地点推荐的精度。
| [1] |
CHORLEY M J, WHITAKER R M, ALLEN S M. Personality and location-based social networks[J]. Computers in Human Behavior, 2015, 46: 45-56. DOI:10.1016/j.chb.2014.12.038 (  0) 0)
|
| [2] |
蒋翠清, 疏得友, 段锐. 基于用户时空相似性的位置推荐算法[J]. 计算机工程, 2018, 44(7): 177-182. (  0) 0)
|
| [3] |
YE Mao, YIN Peifeng.Location recommendation for location-based social networks[C]//Proceedings of ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.New York, USA: ACM Press, 2010: 458-461.
(  0) 0)
|
| [4] |
任星怡, 宋美娜, 宋俊德. 基于用户签到行为的兴趣点推荐[J]. 计算机学报, 2017, 40(1): 28-51. (  0) 0)
|
| [5] |
JANOWICZ K, LEE W C.What you are is when you are: the temporal dimension of feature types in location-based social networks[C]//Proceedings of ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems.New York, USA: ACM Press, 2011: 102-111.
(  0) 0)
|
| [6] |
SERDYUKOV P, HANJALIC A.Personalized landmark recommendation based on geotags from photo sharing sites[C]//Proceedings of the 5th International AAAI Conference on Weblogs and Social Media.Barcelona, Spain: [s.n.], 2011: 622-625.
(  0) 0)
|
| [7] |
WANG Wei, ZHANG Guangquan, LU Jie. Collaborative filtering with entropy-driven user similarity in recommender systems[J]. International Journal of Intelligent Systems, 2015, 30(8): 854-870. DOI:10.1002/int.2015.30.issue-8 (  0) 0)
|
| [8] |
YE Mao, YIN Peifeng.Exploiting geographical influence for collaborative point-of-interest recommendation[C]//Proceedings of International ACM SIGIR Conference on Research and Development in Information Retrieval.New York, USA: ACM Press, 2011: 325-334.
(  0) 0)
|
| [9] |
CHENG Chen, YANG Haiqin.Fused matrix factorization with geographical and social influence in location-based social networks[C]//Proceedings of AAAI Conference on Artificial Intelligence.Toronto, Canada: [s.n.], 2012: 17-23.
(  0) 0)
|
| [10] |
MIKOLOV T, LE Q V, SUTSKEVER I.Exploiting similarities among languages for machine translation[EB/OL].[2018-05-04].https://arxiv.org/pdf/1309.4168v1.pdf.
(  0) 0)
|
| [11] |
MIKOLOV T, SUTSKEVER I.Distributed representations of words and phrases and their compositionality[C]//Proceedings of Advances in Neural Information Processing Systems.[S.l.]: Neural Information Processing Systems Foundation, Inc., 2013: 3111-3119.
(  0) 0)
|
| [12] |
KARYPIS G.Evaluation of item-based top-n recommendation algorithms[C]//Proceedings of the 10th International Conference on Information and Knowledge Management.New York, USA: ACM Press, 2001: 247-254.
(  0) 0)
|
| [13] |
BREESE J S, HECKERMAN D, KADIE C. Empirical analysis of predictive algorithms for collaborative filtering[J]. Uncertainty in Artificial Intelligence, 2013, 98(7): 43-52. (  0) 0)
|
| [14] |
Stackoverflow.Calculate the center point of multiple latitude/longitude coordinate pairs[EB/OL].[2018-05-04].http://stackoverflow.com/questions/6671183/calculate-the-center-point-of-multiple-latitude-longitude-coordinate-pairs.
(  0) 0)
|
| [15] |
YANG Dingqi, ZHANG Daqing. Modeling user activity preference by leveraging user spatial temporal characteristics in LBSNs[J]. IEEE Transactions on Systems Man and Cybernetics Systems, 2014, 45(1): 129-142. (  0) 0)
|
 2019, Vol. 45
2019, Vol. 45

