0 概述

在传统的时间采样控制系统中, 系统状态采样和控制器的更新通常是周期性进行的。当计算和通信资源需要分配给其任务时, 这种时间触发的方式可能使系统处于高工作负载状态。为了节省系统资源, 可以采用非周期性的触发方法。近年来, 人们越来越关注事件触发的反馈控制系统。文献[1-3]描述了关于事件触发机制的一些基本概念。事件触发机制是时间触发机制的替代方案, 在事件触发的方案中, 一旦检测到系统状态偏差不满足给定的事件触发条件, 就会触发控制任务^[4-5]。与时间触发机制中的周期状态采样方式不同, 事件触发中的状态采样是非周期性的。因此, 设计控制器使得其仅在必要时使用计算和通信资源, 可以减少对系统资源的占用, 同时保持良好的稳定性能。研究结果表明, 事件触发机制相较于时间触发机制具有更优的资源节省性能。目前, 多数研究致力于开发设计事件触发机制(ETM)的系统技术, 用于实现给定反馈控制器的系统稳定^[6], 最常用的ETM通常由给定系统状态的等式或不等式组成。事件触发机制多采用文献[7-8]中的多智能体系统, 也常见于多智能体系统的自触发方案设计^[9-10]。

文献[11]研究了基于观测器的事件触发控制的闭环系统。类似于事件触发的输出反馈控制系统的情况^[12], 该系统的输出仅在满足事件触发条件时传输给观测器。通过满足给定的线性矩阵不等式(LMIs)条件和事件触发条件, 可以使反馈控制系统和观测器系统是渐近稳定的。文献[13-14]研究了在某些不确定系统中基于观测器的事件触发状态反馈机制, 通过求解LMIs可以证明系统的稳定性。

通过在事件触发机制中引入一个内部动态变量, 可以得到动态ETM。已有研究学者对ETM中的内部动态变量进行了研究^[15-17]。文献[18-19]中的动态触发机制也引入了内部动态变量, 且提出的机制已经获得了相应的理论成果。与ETM相比, 动态ETM可以降低收敛速度和触发次数, 从而改进ETM的性能。事实证明, 对于大部分事件触发控制器而言, 动态ETM的最小触发间隔大于ETM^[20]。

对于多数事件触发机制研究来说, 系统状态都是已知的。本文针对状态不可测线性系统, 提出一种基于状态观测器输出反馈的动态ETM, 状态观测器利用输出的事件触发信号来估计系统状态。事件触发的控制系统可能会存在Zeno行为, Zeno行为意味着在有限的时间段内存在无数次的触发, 这对于实际物理系统是不允许的。因此, 在实验中给出事件触发控制的最小触发时间间隔, 以排除Zeno行为。

1 基础知识

函数β:R₀⁺→R₀⁺是连续的严格递增的函数且β(0)=0, 则称之为K函数。若存在r→+∞时, β(r)→+∞, 则将β称为K_∞函数。其中, R₀⁺表示非负实数集合。

函数f:Rⁿ→R^m使得对于任意的x, y∈Q⊂Rⁿ, 存在一个常数矩阵M>0且满足式(1)时, 则称该函数是Lipschitz连续的。

$ \left\| {f(x) - f(y)} \right\| \le \mathit{\boldsymbol{M}}\left\| {x - y} \right\| $

(1)

其中, Rⁿ表示n维欧式空间, R^m×n表示所有的m×n维实矩阵的集合。

引理1 ^[21]  若X和Y是实正定矩阵, 则以下不等式成立:

$ {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{Y}} + {\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{X}} \le {\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{Y}} $

(2)

引理2 ^[22] 对于一个对称矩阵S∈R^n×n, 存在$\mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{11}}}&{{\mathit{\boldsymbol{S}}_{12}}}\\ {{\mathit{\boldsymbol{S}}_{21}}}&{{\mathit{\boldsymbol{S}}_{22}}} \end{array}} \right]$, 其中, S₁₁∈R^r×r, S₁₂∈R^r×(n－r), S₂₁∈R^(n－r)×r, S₂₂∈R^{(n－r)×(n－r)}。当S₁₁ < 0, S₂₂－S₁₂^TS₁₁^－1S₁₂ < 0或者S₂₂ < 0, S₁₁－S₁₂S₂₂^－1S₁₂^T < 0时, 存在S < 0。

2 基于观测器事件触发机制

系统状态空间表达式为:

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}}(t) = \mathit{\boldsymbol{Ax}}(t) + \mathit{\boldsymbol{Bu}}(t)}\\ {\mathit{\boldsymbol{y}}(t) = \mathit{\boldsymbol{Cx}}(t)}\\ {\mathit{\boldsymbol{x}}(0) = {\mathit{\boldsymbol{x}}_0}} \end{array}} \right. $

(3)

其中, x∈Rⁿ为系统的状态向量, 初始状态定义为x(0)=x₀, u∈R^m为系统的输入向量, y∈R^q为输出向量。A∈R^n×n, B∈R^n×m和C∈R^q×n均为已知常数矩阵。全维状态观测器为:

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot {\hat x}}} = \mathit{\boldsymbol{A\dot x}}(t) + \mathit{\boldsymbol{Bu}}(t) + \mathit{\boldsymbol{L}}(\mathit{\boldsymbol{y}}(t) - \mathit{\boldsymbol{\hat y}}(t))}\\ {\mathit{\boldsymbol{\hat y}}(t) = \mathit{\boldsymbol{C\hat x}}(t)} \end{array}} \right. $

(4)

其中, $\mathit{\boldsymbol{\hat x}} \in {\mathit{\boldsymbol{R}}^n}$是观测器状态向量, $\mathit{\boldsymbol{\hat y}} \in {\mathit{\boldsymbol{R}}^q}$是观测器输出向量, L∈R^n×q是观测器增益矩阵。假设{A, B}是完全可控的以及{A, C}是完全可观的。

基于观测器的反馈控制器$\mathit{\boldsymbol{u}}(t) = \mathit{\boldsymbol{K}}\mathit{\boldsymbol{\widehat x}}(t), \mathit{\boldsymbol{K}}$是反馈增益矩阵。定义观测器状态误差为$\mathit{\boldsymbol{\tilde x}}\left( t \right) = \mathit{\boldsymbol{x}}(t) - \mathit{\boldsymbol{\hat x}}(t)$, 可以得到观测误差的动态方程为$\mathit{\boldsymbol{\dot {\tilde x}}}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})\mathit{\boldsymbol{\tilde x}}(t)$。

2.1 事件触发机制

实验将引入事件触发机制改善系统的性能。假设系统式(3)的输出信号仅在t_k, k∈Z₀⁺时刻更新, 输出信号即可表示为:y(t)=y(t_k), t∈[t_k, t_k+1), 重新得到观测器的表达式为: $\mathit{\boldsymbol{\dot {\hat x}}}(t) = \mathit{\boldsymbol{A}}\mathit{\boldsymbol{\widehat x}}(t) + \mathit{\boldsymbol{Bx}}(t) + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{y}}\left( {{t_k}} \right) - \mathit{\boldsymbol{\widehat y}}(t)} \right)$。

定义输出误差为:

$ {\mathit{\boldsymbol{e}}_y}(t) = \mathit{\boldsymbol{y}}({t_k}) - \mathit{\boldsymbol{y}}(t),t \in [{t_k},{t_{k + 1}}) $

(5)

因此, 可以描述系统状态和观测器状态误差为:

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot x}}(t) = (\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{x}}(t) - \mathit{\boldsymbol{B\tilde Kx}}(t)}\\ {\mathit{\boldsymbol{\dot {\tilde x}}}(t) = (\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})\mathit{\boldsymbol{\tilde x}}(t) - \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{e}}_y}(t)} \end{array}} \right. $

(6)

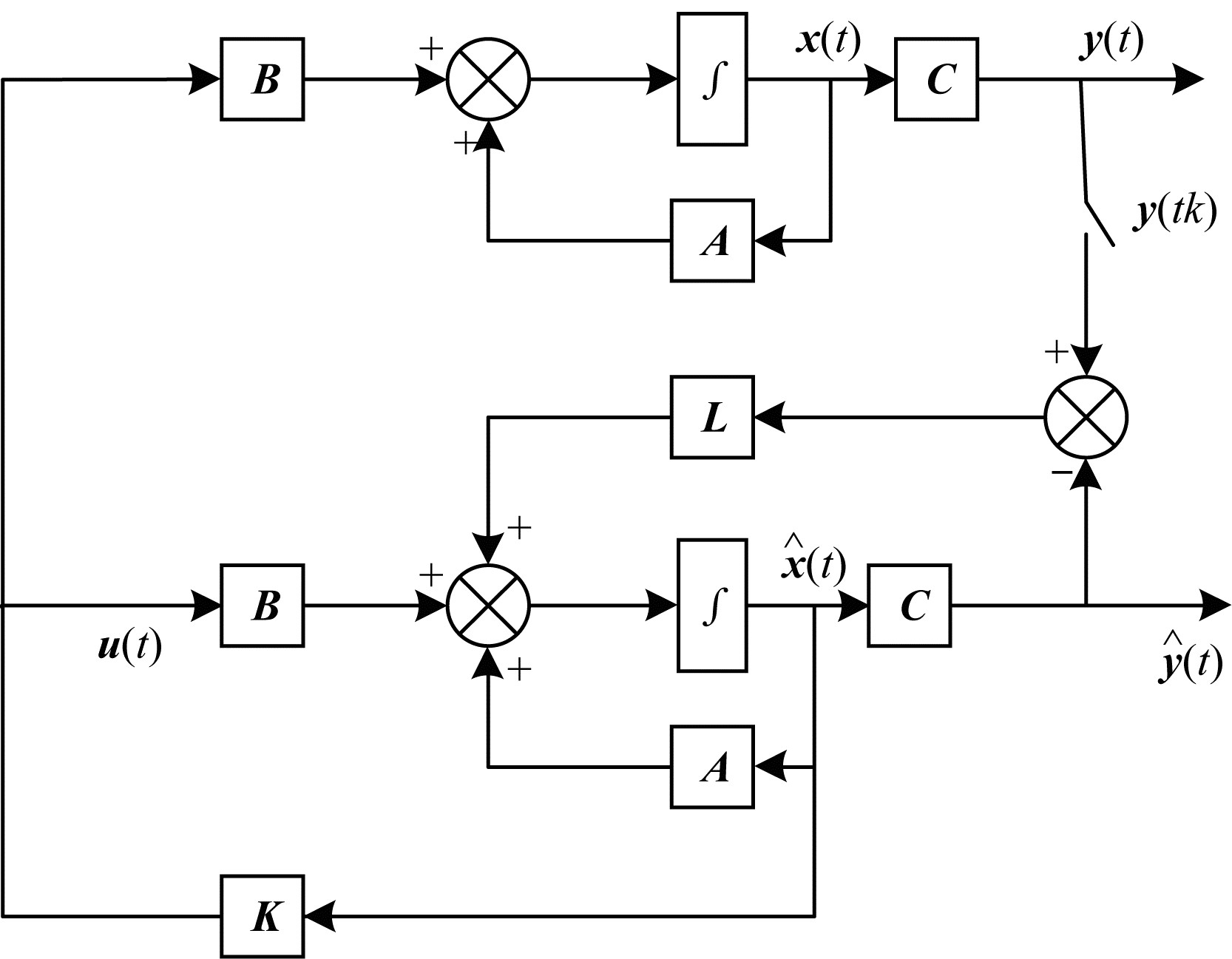
事件触发机制系统结构如图 1所示。

定义事件触发条件为:

$ \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t) < \sigma {\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{y}}(t),\sigma \in [0,1) $

(7)

其中, σ为给定的常数。当不满足式(7)时, 对系统输出信号进行更新。

定理1  在系统式(6)中, 如果存在2个正定矩阵P₁, P₂∈R^n×n, 以及正数σ∈[0, 1)满足以下2个矩阵不等式(8)与式(9):

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_1}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}) + {{(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1} + \sigma {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}}}&{{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{BK}}}\\ {{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1}}&{ - {\mathit{\boldsymbol{I}}_{\rm{n}}}} \end{array}} \right] < 0 $

(8)

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_2}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}) + {{(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + {\mathit{\boldsymbol{I}}_n}}&{{\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{L}}}\\ {{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2}}&{ - {\mathit{\boldsymbol{I}}_q}} \end{array}} \right] < 0 $

(9)

则系统式(6)是渐近稳定的, 且有$\mathop {\lim }\limits_{t \to \infty } x(t) = 0, \mathop {\lim }\limits_{t \to \infty } \tilde x(t) = 0$。

证明  构造Lyapunov函数为:

$ V(\mathit{\boldsymbol{x}}(t),\mathit{\boldsymbol{\tilde x}}(t)) = {\mathit{\boldsymbol{x}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{x}}(t) + {\mathit{\boldsymbol{\tilde x}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{\tilde x}}(t) $

其中, P₁, P₂分别为矩阵不等式(8)和式(9)的解, 对Lyapunov函数关于时间求导可以得到:

$ \begin{array}{l} \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot V}} = {{\mathit{\boldsymbol{\dot x}}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{x}}(t) + {\mathit{\boldsymbol{x}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{\dot x}}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\dot {\tilde x}}}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{\tilde x}}(t) + {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{\dot {\tilde x}}}(t) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{((\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{x}}(t) - \mathit{\boldsymbol{B\tilde Kx}}(t))}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{x}}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{x}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_1}((\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{x}}(t) - \mathit{\boldsymbol{B\tilde Kx}}(t)) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ((\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})\mathit{\boldsymbol{\tilde x}}(t) - \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{e}}_y}(t)){\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{\tilde x}}(t) + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_2}((\mathit{\boldsymbol{L}} - \mathit{\boldsymbol{LC}})\mathit{\boldsymbol{\tilde x}}(t) - \mathit{\boldsymbol{L}}{\mathit{\boldsymbol{e}}_y}(t)) = }\\ {{\mathit{\boldsymbol{x}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_1}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}) + {{(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1})\mathit{\boldsymbol{x}}(t) + }\\ {{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_2}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}) + {{(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2})\mathit{\boldsymbol{\tilde x}}(t) - }\\ {2{\mathit{\boldsymbol{x}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{B\tilde Kx}}(t) - 2\mathit{\boldsymbol{\tilde x}}(t){\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{e}}_y}(t) \le } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_1}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}) + {{(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1})\mathit{\boldsymbol{x}}(t) + }\\ {{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_2}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}) + {{(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2})\mathit{\boldsymbol{\tilde x}}(t) + }\\ {{\mathit{\boldsymbol{x}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{BK}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{x}}(t) + {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)\mathit{\boldsymbol{\tilde x}}(t) + }\\ {{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t){\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{\tilde x}}(t) + \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t)} \end{array} \end{array} $

(10)

由事件触发机制可知, 若式(7)不满足, 则会有第k+1次更新执行。因此, 通过计算可以得到:

$ \begin{array}{*{20}{l}} {\dot V \le {\mathit{\boldsymbol{x}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_1}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}) + {{(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{BK}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1} + \sigma {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}})\mathit{\boldsymbol{x}}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_2}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}) + {{(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})}^{\rm{T}}}\mathit{\boldsymbol{P}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + \mathit{\boldsymbol{I}})\mathit{\boldsymbol{\tilde x}}(t)} \end{array} $

(11)

由引理1可知, 不等式(8)、不等式(9)分别与以下不等式(12)、不等式(13)等价:

$ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_1}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}) + {{(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1} + }\\ {{\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{BK}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1} + \sigma {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}} < 0} \end{array} $

(12)

$ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_2}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}) + {{(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + }\\ {{\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + \mathit{\boldsymbol{I}} < 0} \end{array} $

(13)

因此, 可以证明$\dot V(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tilde x}}) < 0$, 即系统式(6)是渐近稳定的。

备注1  通过求解线性矩阵不等式(8)和不等式(9), 可以得到参数σ以及P₁和P₂的值。这些参数值在事件触发条件式(7)下可以保证系统状态和观测器误差状态的渐近稳定性。此外, 这2个线性矩阵不等式互相独立。事件触发策略的设计仅仅与控制器增益矩阵K有关, 而与观测器本身无关, 这显示了事件触发方案的设计与观测器之间的分离原则。

令2个对称正定矩阵M, N∈R^n×n满足以下等式:

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{M}} = - ({\mathit{\boldsymbol{P}}_1}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}) + {{(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{BK}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1})} \end{array} $

(14)

$ \begin{array}{l} \mathit{\boldsymbol{N}} = - ({\mathit{\boldsymbol{P}}_2}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}) + {(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + \mathit{\boldsymbol{I}}) \end{array} $

(15)

可以得到:

$ \begin{array}{l} \begin{array}{*{20}{l}} {\dot V \le {\mathit{\boldsymbol{x}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_1}(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}}) + {{(\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_1}\mathit{\boldsymbol{BK}}{\mathit{\boldsymbol{K}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_1})\mathit{\boldsymbol{x}}(t) + \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)({\mathit{\boldsymbol{P}}_2}(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}) + {{(\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}})}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_2}\mathit{\boldsymbol{L}}{\mathit{\boldsymbol{L}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_2} + \mathit{\boldsymbol{I}})\mathit{\boldsymbol{\tilde x}}(t) = } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} { - {\mathit{\boldsymbol{x}}^{\rm{T}}}(t)\mathit{\boldsymbol{Mx}}(t) + \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t) - {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)\mathit{\boldsymbol{N\tilde x}}(t) = }\\ {{\mathit{\boldsymbol{x}}^{\rm{T}}}(t)(\sigma {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}} - \mathit{\boldsymbol{M}})\mathit{\boldsymbol{x}}(t) - {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)\mathit{\boldsymbol{Nx}}(t)} \end{array} \end{array} $

(16)

事件触发时刻有以下不等式e_y^T(t)e_y(t)≥σy^T(t)y(t), 则ETM的时间序列{t_k}_k∈Z0⁺可以定义为:

$ {t_{k + 1}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_{t > {t_k}} \left\{ {\begin{array}{*{20}{l}} {t|\sigma {\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{y}}(t)}\\ { - \mathit{\boldsymbol{e}}_t^{\rm{T}}({t^ - }){\mathit{\boldsymbol{e}}_y}({t^ - }) \le 0} \end{array}} \right\} $

(17)

该事件触发机制意味着σy^T(t)y(t)－e_y^T(t)e_y(t)的值始终是非负的, 因此有$\frac{{{\rm{d}}V(\mathit{\boldsymbol{x}}(t), \mathit{\boldsymbol{\widetilde x}}(t))}}{{{\rm{d}}t}} < 0$, 保证了x(t)和${\mathit{\boldsymbol{\widetilde x}}(t)}$在t→∞时渐近收敛。

事件触发策略式(17)仅受x、${\mathit{\boldsymbol{\widetilde x}}}$、e_y当前值的影响。下文中提出了动态ETM, 引用一个额外的内部动态变量。动态ETM不仅与当前时刻状态有关, 而且还受之前状态的影响。

2.2 动态事件触发机制

通过使用动态ETM, 系统可以进一步减少触发次数, 从而可以实现更好的资源节省性能。基于满足以下微分方程的内部动态变量η引入动态ETM:

$ \begin{array}{*{20}{l}} {\dot \eta (t) = - \beta (\eta (t)) + \sigma {\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{y}}(t) - \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t)}\\ {\eta (0) = {\eta _0}} \end{array} $

(18)

其中, β是K_∞类函数, 并且满足Lipschitz连续性。σ>0和η₀∈R₀⁺是已知参数。根据β可以是线性或非线性的, 系统式(3)可以保持稳定性, 并且不需要必须保持σy^Ty－e_y^Te_y非负。这可以通过事件触发这样的方式来确保, 即η始终保持非负值。则动态ETM由以下规则定义:

$ {t_{k + 1}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_{t > {t_k}} \left\{ {\begin{array}{*{20}{l}} {t|\eta (t) + \theta [\sigma {\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{y}}(t)}\\ { - \mathit{\boldsymbol{e}}_y^{\rm{T}}({t^ - }){\mathit{\boldsymbol{e}}_y}({t^ - })] \le 0} \end{array}} \right\} $

(19)

其中, θ∈R₀⁺是一个额外设计的参数, 其中事件触发机制式(17)可以视为动态事件触发机制在θ→+∞时的特殊情况。

引理3  假设β是K_∞函数且满足Lipschitz连续性, 令σ∈[0, 1), η, θ∈R₀⁺。假设x、e_y和η分别由式(3)、式(5)、式(18)定义, 那么对任意的t∈[0, ∞)时, 存在:

$ {\eta (t) + \theta (\sigma {\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{y}}(t) - \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t)) \ge 0} $

(20)

$ {\eta (t) \ge 0} $

(21)

证明  动态触发条件式(19)确保了对任意的t∈[0, ∞)均有:η(t)+θ(σy^T(t)y(t)－e_y^T(t^－)e_y(t^－))≥0。

由于e_y(t)是连续的且对任意的t∈[0, ∞)都满足e_y^T(t)e_y(t)≤e_y^T(t^－)e_y(t^－), 因此不等式(20)得证。如果θ∈0, 不等式(21)则是不等式(20)的一个特例, 因此存在η(t)≥0。若θ≠0, 通过不等式(20)可以得到:

$ \sigma {\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{y}}(t) - \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t) \ge - \frac{1}{\theta }\eta (t) $

(22)

通过式(18)可以得到:

$ \dot \eta (t) \ge - \beta (\eta (t)) - \frac{1}{\theta }\eta (t),\eta (0) \ge 0 $

(23)

通过比较和分析可知, 对任意的t∈[0, ∞)都满足η(t)≥0, 因此, η在任意时刻都保证是非负的。

定理2  对任意的σ∈[0, 1), η, θ∈R₀⁺, 在动态事件触发条件式(19)下, x(t)、$ {\mathit{\boldsymbol{\widetilde x}}(t)}$和η(t)渐近收敛。

证明  定义Lyapunov函数W:Rⁿ×R₀⁺→R₀⁺来证明系统的稳定性, 令:

$ W(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\tilde x}},\eta ) = V(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\tilde x}}) + \eta $

(24)

显然, W是正的并且径向无界, 且对任意的$(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tilde x}}, \eta ) \in {\mathit{\boldsymbol{R}}^n} \times \mathit{\boldsymbol{R}}_0^ + $均有$W(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tilde x}}, \eta ) > V(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tilde x}})$成立。同样, 根据不等式(16)与不等式(18), $W(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\tilde x}}, \eta )$关于时间的导数满足:

$ \begin{array}{*{20}{l}} {\dot W = \dot V(\mathit{\boldsymbol{x}}(t),\mathit{\boldsymbol{\tilde x}}(t)) + \dot \eta (t) \le }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\mathit{\boldsymbol{x}}^{\rm{T}}}(t)\mathit{\boldsymbol{Mx}}(t) + \mathit{\boldsymbol{e}}_y^{\rm{T}}(t){\mathit{\boldsymbol{e}}_y}(t) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)\mathit{\boldsymbol{N\tilde x}}(t) + \dot \eta (t) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - {\mathit{\boldsymbol{x}}^{\rm{T}}}(t)\mathit{\boldsymbol{Mx}}(t) - {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)\mathit{\boldsymbol{N\tilde x}}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma {\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{y}}(t) - \beta (\eta (t)) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{x}}^{\rm{T}}}(t)(\sigma {\mathit{\boldsymbol{C}}^{\rm{T}}}\mathit{\boldsymbol{C}} - \mathit{\boldsymbol{M}})\mathit{\boldsymbol{x}}(t) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}(t)\mathit{\boldsymbol{N\tilde x}}(t) - \beta (\eta (t))} \end{array} $

(25)

由于β是K_∞函数且满足Lipschitz连续性, 同时有$\sigma > 0, \frac{{{\rm{d}}W(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{\widetilde x}}, \eta )}}{{{\rm{d}}t}} \le 0$。

W是衰减的, 当t→+∞时, x(t)、${\mathit{\boldsymbol{\widetilde x}}}$和η(t)渐近收敛于原点。

备注2  提出的动态ETM有几个设计参数, η, σ∈(0, 1)以及θ∈R₀⁺。这些参数主要影响触发间隔的下界和系统状态的收敛速度, 实验需要提供一些论证来指导选择参数值。首先, 触发间隔的下界是θ的连续函数。实际上, ETM可以被视为动态ETM的极限情况, 其中θ→+∞。其次, 闭环系统式(6)的收敛与σ直接相关, 通过适当选择参数σ可以调节衰减率, 也可以通过改变σ值来控制事件触发的次数。通过调整σ和θ, 可以接近理想闭环系统式(6)的性能。最后, 尽量选择合适的σ和θ, 以减少对性能指标的影响。

2.3 Zeno行为分析

事件触发机制中的一个重要问题为是否存在最小的触发间隔τ>0, 对任意的时间序列{t_k}_k∈Z0⁺都满足t_k+1－t_k≥τ, ∀k∈Z₀⁺。下文将提出一种动态触发机制的方法来排除Zeno行为。

事件触发条件式(7)等价于$\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\| < \sqrt \sigma \left\| {\mathit{\boldsymbol{y}}(t)} \right\|$, 由于y=Cx, 因此有$\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\| < \sqrt \sigma \left\| \mathit{\boldsymbol{C}} \right\|\left\| {\mathit{\boldsymbol{x}}(t)} \right\|$, 同时$\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\| < \sqrt \sigma \left\| \mathit{\boldsymbol{C}} \right\|\left\| {\mathit{\boldsymbol{\widetilde x}}(t) + \mathit{\boldsymbol{\widehat x}}(t)} \right\|$, 则不等式成立:

$ \left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\| < \sqrt \sigma \left\| \mathit{\boldsymbol{C}} \right\|(\left\| {\mathit{\boldsymbol{\tilde x}}(t)} \right\| + \left\| {\mathit{\boldsymbol{\hat x}}(t)} \right\|) $

(26)

令:

$ \left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\| < \sqrt \sigma \left\| \mathit{\boldsymbol{C}} \right\|\left\| {\mathit{\boldsymbol{\tilde x}}(t)} \right\| $

(27)

若不等式(27)成立, 则一定存在不等式(7)成立, 同样能保证系统式(3)的渐近稳定性。因此, 有$\left\| {\mathit{\boldsymbol{\tilde x}}(t)} \right\| > \frac{1}{{\sqrt \sigma \left\| \mathit{\boldsymbol{C}} \right\|}}\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|$, 由于σ∈(0, 1), 可以得到$\left\| {\mathit{\boldsymbol{\tilde x}}(t)} \right\| > \frac{1}{{\left\| \mathit{\boldsymbol{C}} \right\|}}\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|$或者可以得到$ - \left\| {\mathit{\boldsymbol{\tilde x}}(t)} \right\| < - \frac{1}{{\left\| \mathit{\boldsymbol{C}} \right\|}}\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|$, 则可将系统的状态空间描述为:

$ \begin{array}{l} \mathit{\boldsymbol{\dot x}}(t) = (\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{x}}(t) - \mathit{\boldsymbol{B\tilde Kx}}(t) \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{x}}(t) - \frac{{\mathit{\boldsymbol{BK}}}}{{\left\| \mathit{\boldsymbol{C}} \right\|}}\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\| \le \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{BK}})\mathit{\boldsymbol{x}}(t) + \frac{{\mathit{\boldsymbol{BK}}}}{{\left\| \mathit{\boldsymbol{C}} \right\|}}\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\| \end{array} $

(28)

推论1  对于闭环系统式(3)以及控制律$\mathit{\boldsymbol{u}} = \mathit{\boldsymbol{K\hat x}}$, 在事件触发条件式(7)下任意的时间序列{t_k+1－t_k}, 都存在一个正的最小的时间下界τ:

$ \tau = \frac{1}{{p - q}}{\rm{ln}}\frac{{p\sqrt \sigma + q}}{{q\sqrt \sigma + q}} $

(29)

其中, $q = \left\| \mathit{\boldsymbol{A}} \right\| + \left\| {\mathit{\boldsymbol{BK}}} \right\|, p = \left\| {\mathit{\boldsymbol{BK}}} \right\|$。

证明  利用式(28)的结论, 可以通过以下变量的导数得到触发间隔下限:

$ \begin{array}{l} \begin{array}{*{20}{l}} {\frac{{{\rm{d}}\frac{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}}}}{{{\rm{d}}t}} = \frac{{\mathit{\boldsymbol{e}}_y^{\rm{T}}(t){{\mathit{\boldsymbol{\dot e}}}_y}(t)}}{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}} - \frac{{{\mathit{\boldsymbol{y}}^{\rm{T}}}(t)\mathit{\boldsymbol{\dot y}}(t)}}{{{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}^2}}}\frac{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}} \le }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\left\| {\mathit{\boldsymbol{e}}_y^{\rm{T}}(t)} \right\|\left\| {\mathit{\boldsymbol{\dot y}}(t)} \right\|}}{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}} + \frac{{\left\| {\mathit{\boldsymbol{\dot y}}(t)} \right\|\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}^2}}} = } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\left( {1 + \frac{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}}} \right)\frac{{\left\| {\mathit{\boldsymbol{\dot y}}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}} = }\\ {\left( {1 + \frac{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}}} \right)\frac{{\left\| {\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}} \le }\\ {\left( {1 + \frac{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}}} \right)\frac{{q\left\| {\mathit{\boldsymbol{y}}(t)} \right\| + p\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}} \le }\\ {\left( {1 + \frac{{\left\| {{\mathit{\boldsymbol{e}}_y}(t)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}}} \right)\left( {q + p\frac{{\left\| {{\mathit{\boldsymbol{e}}_{y(t)}}} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}(t)} \right\|}}} \right)} \end{array} \end{array} $

(30)

令$\phi = \frac{{\left\| {{\mathit{\boldsymbol{e}}_y}\left( t \right)} \right\|}}{{\left\| {\mathit{\boldsymbol{y}}\left( t \right)} \right\|}}$, 可以简化式(30)为:

$ \dot \phi \le (1 + \phi )(q + p\phi ) $

(31)

令初始条件为ϕ(0)=0, 通过求解式(31)可以得到:

$ \phi (t) = \frac{{q - q{\mathit{\boldsymbol{e}}^{(p - q)t}}}}{{q{\mathit{\boldsymbol{e}}^{(p - q)t}} - p}} $

(32)

其中, $q = \left\| \mathit{\boldsymbol{A}} \right\| + \left\| {\mathit{\boldsymbol{BK}}} \right\|, p = \left\| {\mathit{\boldsymbol{BK}}} \right\|$。根据式(10)可知:

$ \phi (\tau ) = \sqrt \sigma ,\phi (0) = 0 $

因此, 可以得到事件触发最小时间下界τ为:

$ \tau = \frac{1}{{p - q}}{\rm{ln}}\frac{{p\sqrt \sigma + q}}{{q\sqrt \sigma + q}} $

(33)

其中, $q = \left\| \mathit{\boldsymbol{A}} \right\| + \left\| {\mathit{\boldsymbol{BK}}} \right\|, p = \left\| {\mathit{\boldsymbol{BK}}} \right\|$均大于0, 且q>p, 则存在:

$ {\frac{{p\sqrt \sigma + q}}{{q\sqrt \sigma + q}} < 1} $

(34)

$ {{\rm{ln}}\frac{{p\sqrt \sigma + q}}{{q\sqrt \sigma + q}} < 0} $

(35)

因此τ>0。事件触发机制不存在Zeno行为。

推论表明, 对于系统给定的状态, 动态ETM给出的下一个执行时间大于ETM给出的时间。

推论2  对于给定的β为Lipschtiz连续的K_∞函数, σ>0, η₀, θ∈R₀⁺, 令k∈Z₀⁺, t_k∈R₀⁺, x(t_k)∈Rⁿ和η(t_k)≥0。令t_k+1^s为事件触发时刻, t_k+1^d为动态事件触发时刻, 那么有t_k+1^s≤t_k+1^d。

证明   假设t_k+1^s>t_k+1^d, 通过式(17)可以得到:

$ \sigma \left\| {\mathit{\boldsymbol{y}}(t_{k + 1}^d)} \right\| - {\left\| {{\mathit{\boldsymbol{e}}_y}(t_{k + 1}^{d - })} \right\|^2} > 0 $

(36)

当θ>0时, 由式(19)和引理3可以得到:

$ \begin{array}{*{20}{l}} {0 \ge \eta (t_{k + 1}^d) + \theta (\sigma {{\left\| {\mathit{\boldsymbol{y}}(t_{k + 1}^d)} \right\|}^2} - {{\left\| {{\mathit{\boldsymbol{e}}_y}(t_{k + 1}^{d\_})} \right\|}^2}) \ge }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta (\sigma \left\| {\mathit{\boldsymbol{y}}(t_{k + 1}^d)} \right\| - {{\left\| {{\mathit{\boldsymbol{e}}_y}(t_{k + 1}^{d\_})} \right\|}^2})} \end{array} $

(37)

这与式(36)互相矛盾, 因此t_k+1^s≤t_k+1^d。

如果θ=0, 那么由事件触发条件式(19)可知η(t^d_k+1)=0且η·(t_k+1^d_－)≤0, 通过式(18)又得到0≥η·(t_k+1^d_－)=σ‖y(t_k+1^d)‖－‖e_y(t_k+1^d_－)‖²。这同样与式(36)互相矛盾, 因此t_k+1^s≤t_k+1^d。可以得出结论, 动态ETM式(19)的最小触发间隔不会小于ETM式(17)的执行时间。类似的, 可以选取较小的参数θ得到一个较大的最小触发间隔时间, 同时意味着动态触发的闭环系统不会存在Zeno行为。

3 模拟仿真

使用一个例子来验证理论结果的有效性。考虑形式为式(3)的线性系统为:

$ {\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - 0.8}&{0.2}\\ 1&0 \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{l}} 1\\ 0 \end{array}} \right]} $

$ {\mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{l}} { - 0.65}&{6.85} \end{array}} \right],{\mathit{\boldsymbol{x}}_0} = \left[ {\begin{array}{*{20}{c}} { - 0.2}\\ {0.4} \end{array}} \right]} $

系统很明显是完全可控可观的。

反馈增益由极点配置设计, 极点选取为{－0.2, －0.7}, 可以得到K=－0.1－0.34, 而观测器的增益是将观测器系统的极点置于{－3, －4}, 可以得到$\mathit{\boldsymbol{L}} = \left[ \begin{array}{l} 1\\ 1 \end{array} \right]$, L作为观测器的输出误差反馈矩阵, 使得${\mathit{\boldsymbol{\hat x}}}$可以渐近收敛到x。

通过求解触发条件式(7)可以得到矩阵P₁的值以及σ=0.003 1, 事件触发条件就为e_y^T(t)e_y(t)<0.003 1y^T(t)y(t), 且${\mathit{\boldsymbol{p}}_1} = \left[ {\begin{array}{*{20}{c}} {7.530{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 6}&{0.946{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 5}\\ {0.946{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 5}&{1.078\;\;3} \end{array}} \right]$。

求解LMI式(8)可以得到矩阵P₂值为${\mathit{\boldsymbol{p}}_2} = \left[ {\begin{array}{*{20}{c}} {1.042\;\;2}&{ - 0.770\;\;3}\\ { - 0.770\;\;3}&{0.956\;\;5} \end{array}} \right]$。

实验选取β(η)=λη是满足Lipschitz连续的K_∞函数。关于λ和θ的参数, 为了显示更好的效果, 参数选取为λ=0.01, σ=0.003 1和θ=1。这些参数选取符合具有动态触发机制的事件触发机制要求。

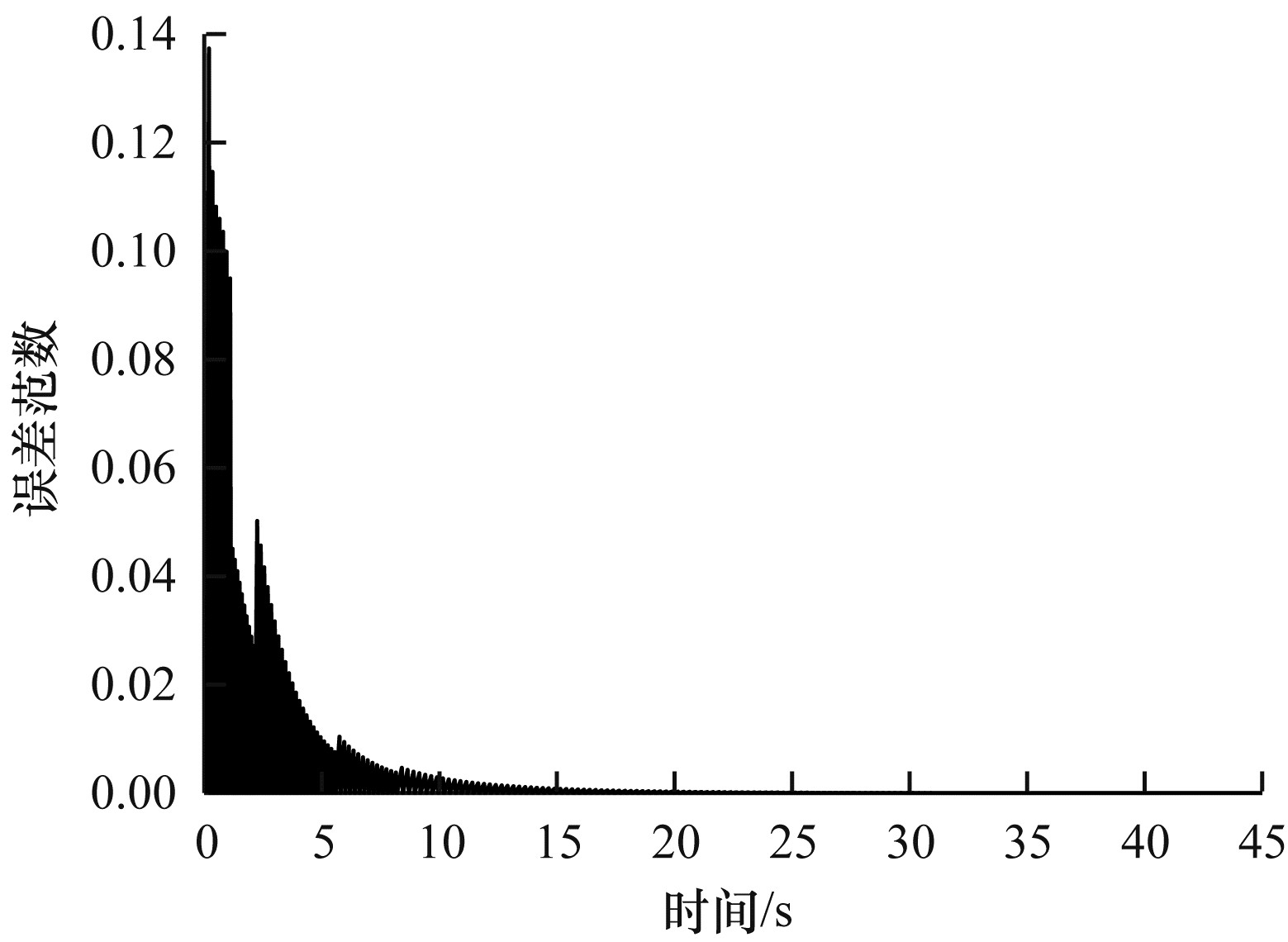
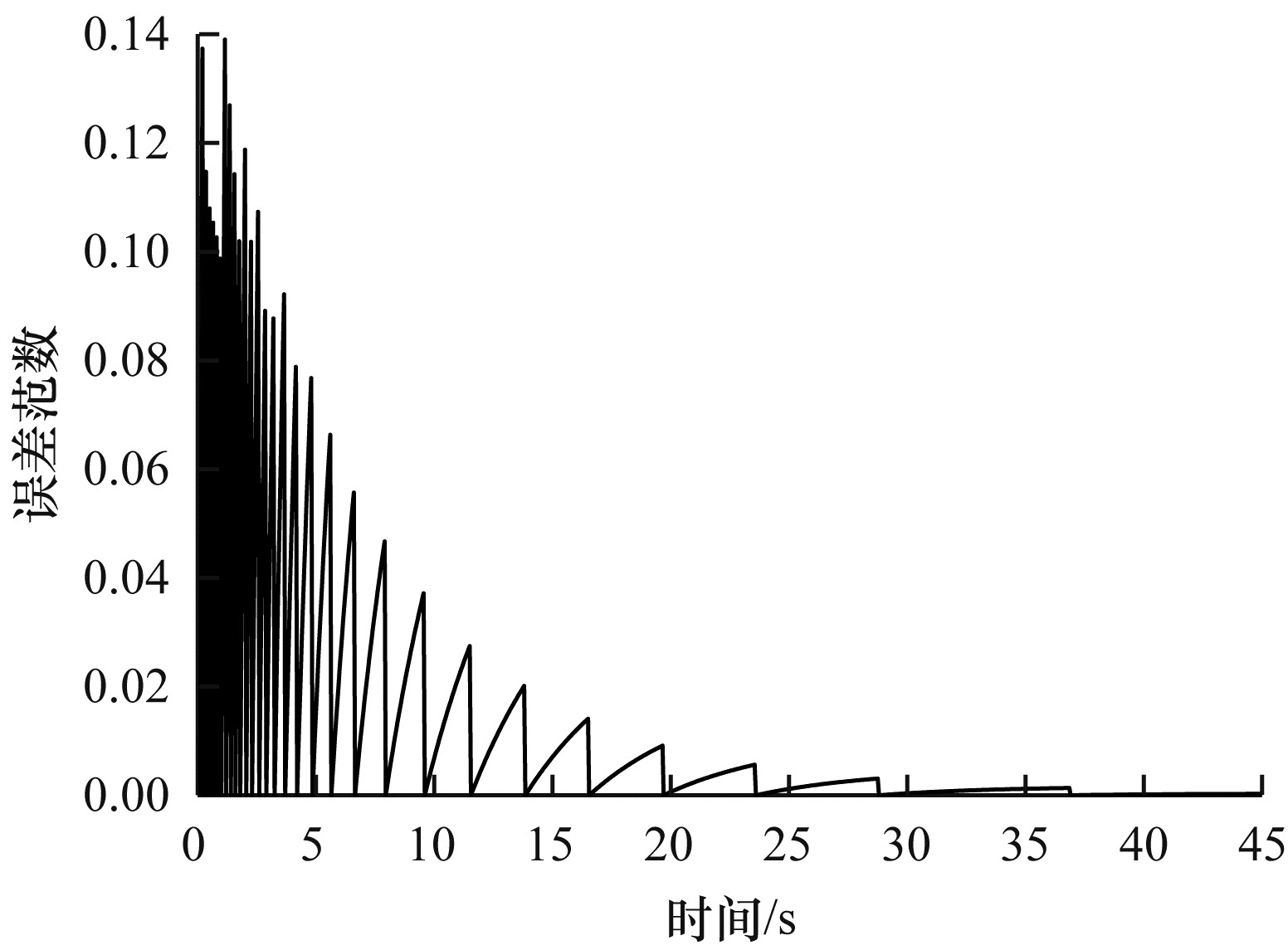
图 2显示了ETM的误差范数, 误差范数一旦达到阈值, 它就会重置为0。图 3显示了动态ETM的误差范数, 当误差范数达到阈值时, 它也会重置为0。从图中可以看出, 动态ETM可容许较大的误差范数阈值, 这是由事件触发条件决定的。ETM的触发次数为201, 动态ETM的触发次数为30, 与ETM相比, 动态ETM减少了触发次数。

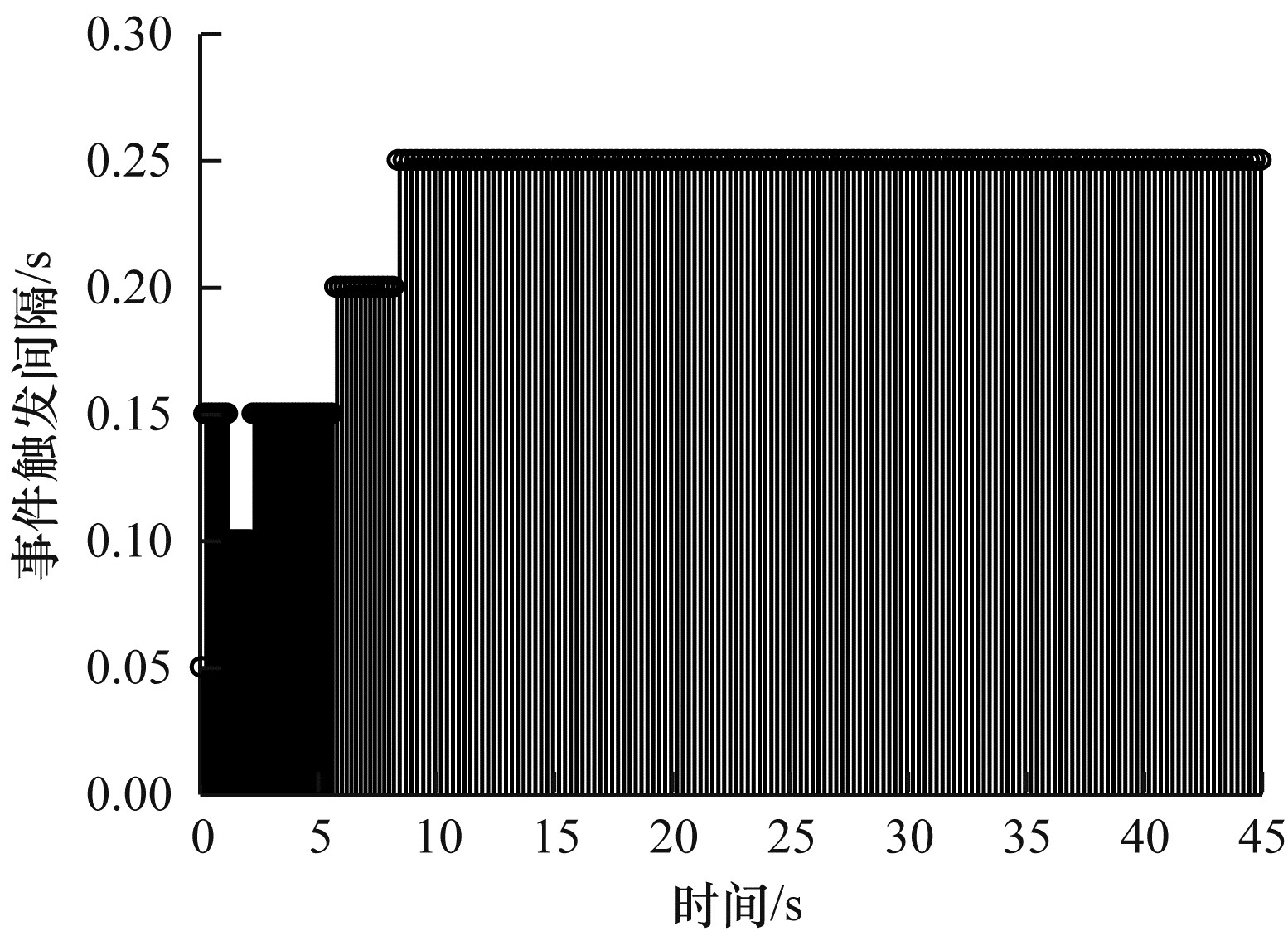
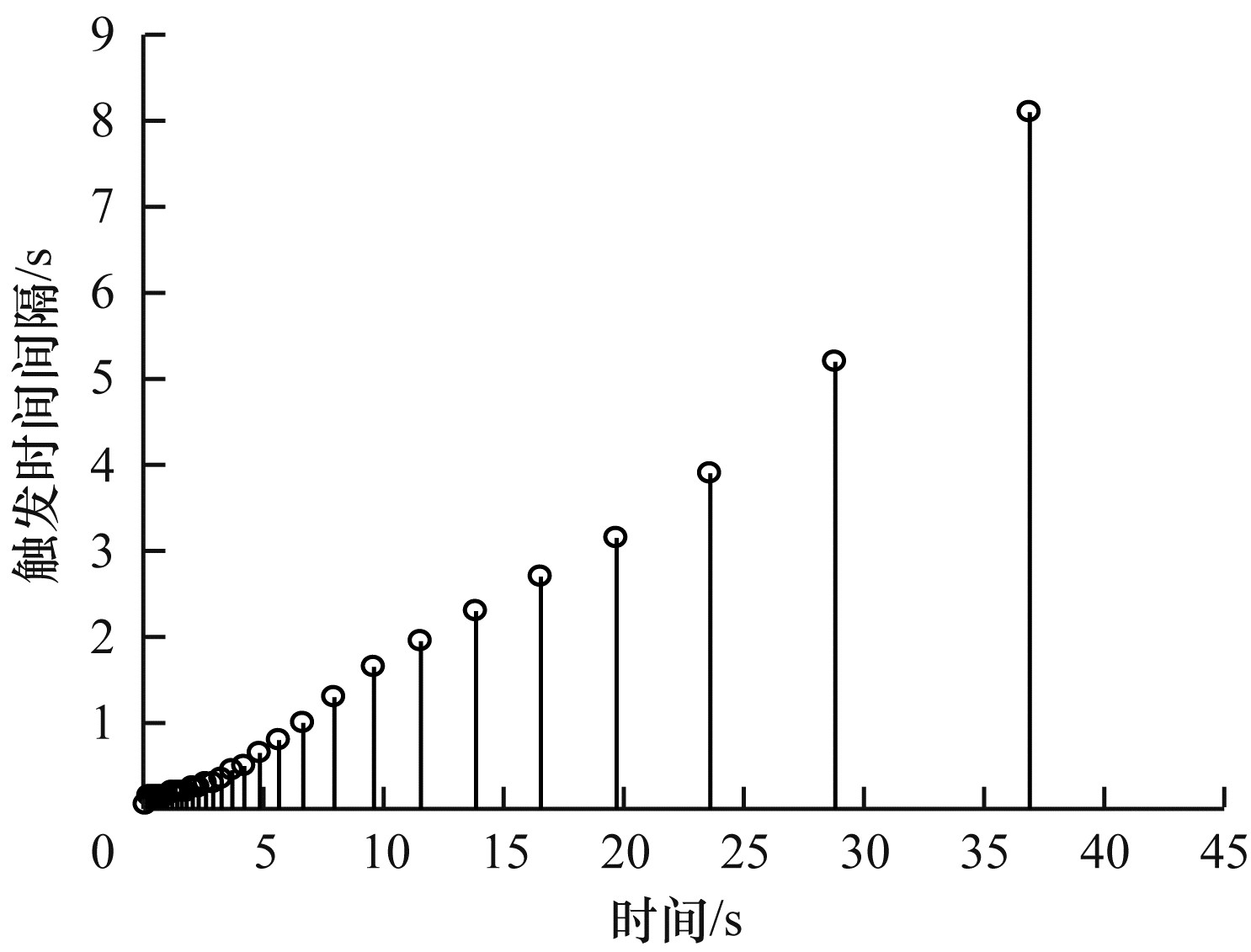
基于观测器ETM的平均触发时间间隔如图 4所示, 触发时间间隔的平均值为0.224 s。图 5所示为基于观测器的动态ETM事件触发机制的平均触发时间间隔, 平均触发时间间隔为1.500 s。ETM的触发时间间隔的平均值远小于动态ETM的平均触发时间间隔。

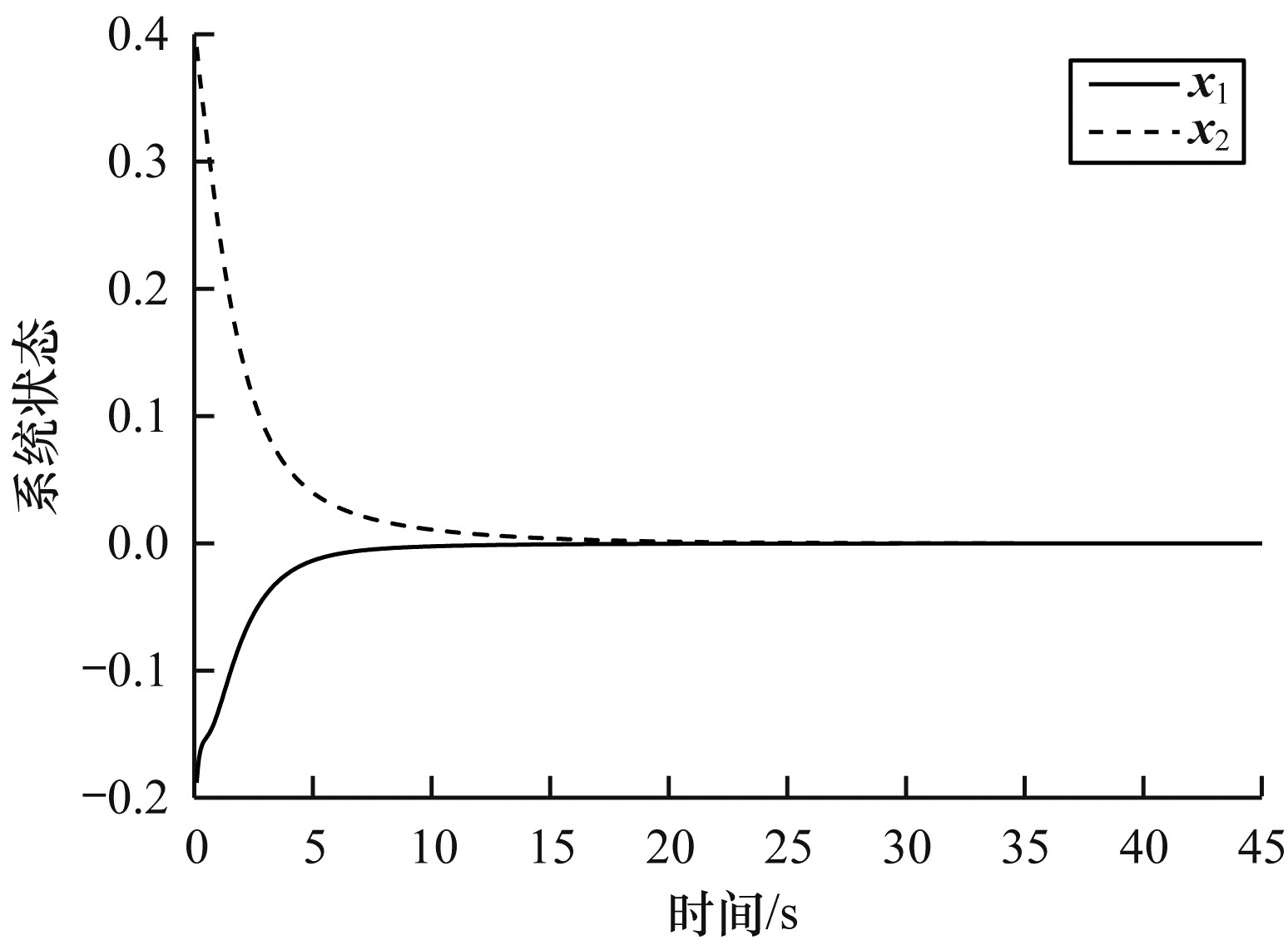
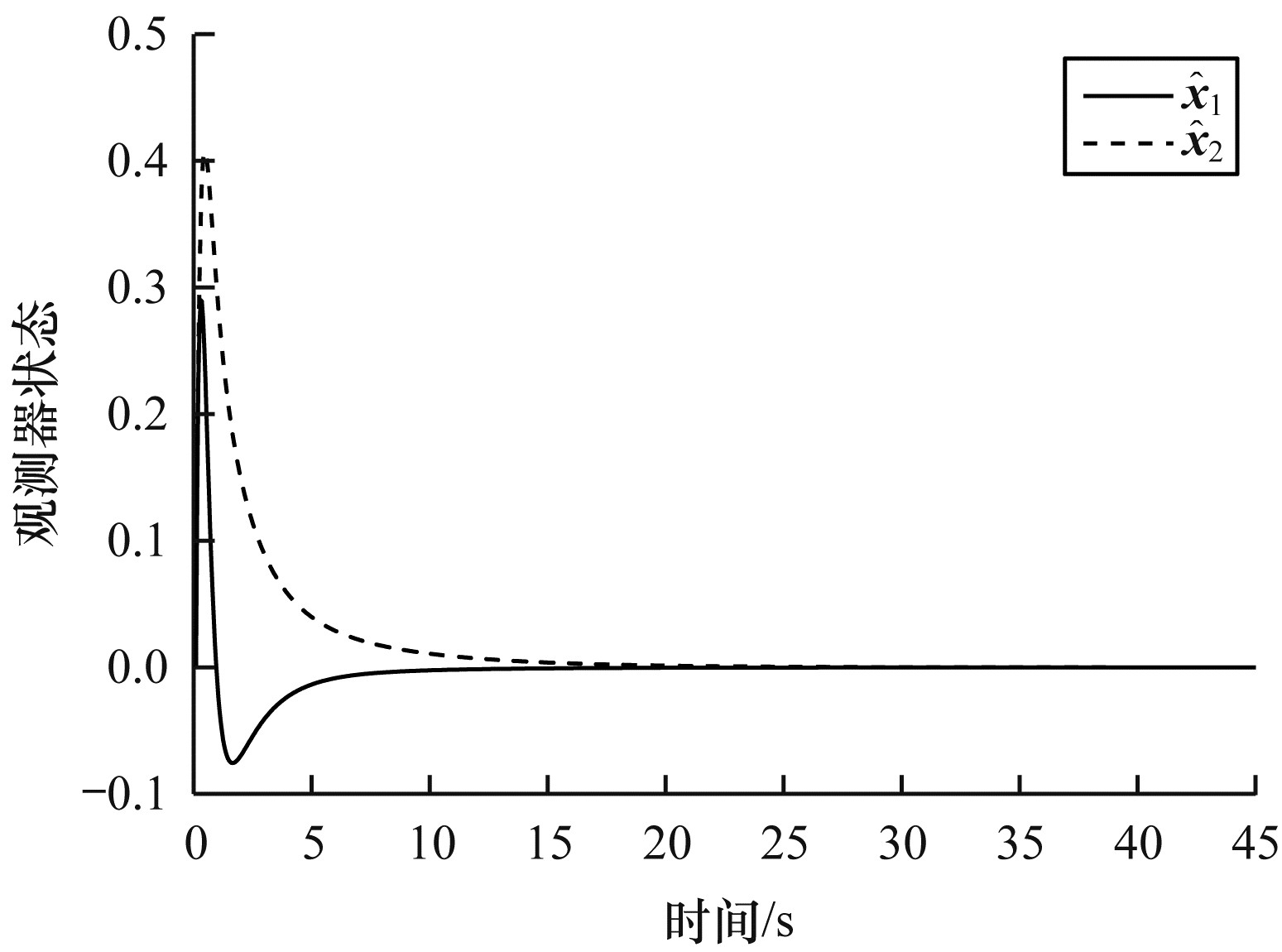
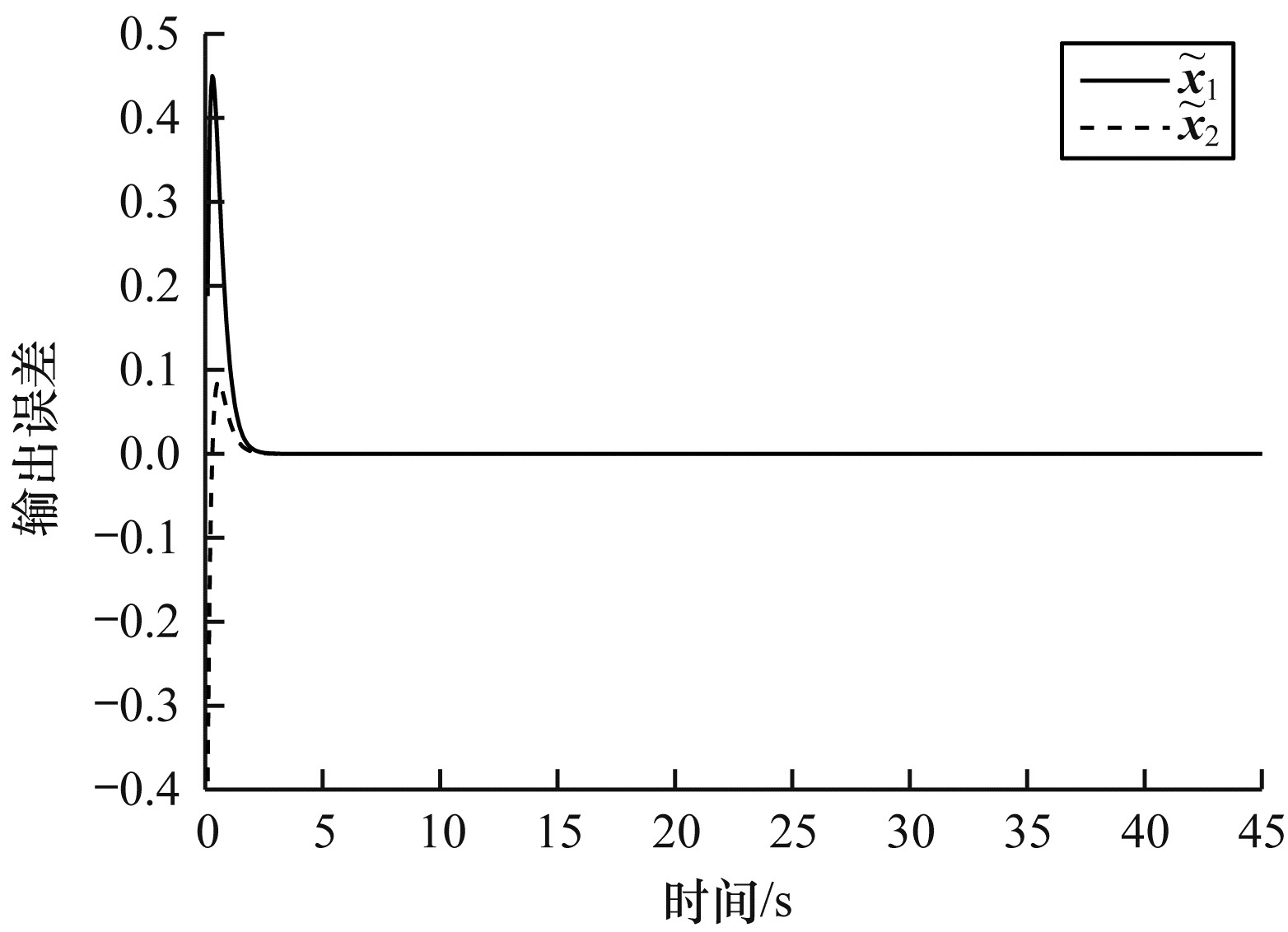
图 6、图 7和图 8中的状态轨迹展示了基于观测器的动态ETM事件触发机制系统的渐近稳定性。图 6显示了系统的状态轨迹, 从图 6可以看出, 系统的状态由初始值[-0.2, 0.4]逐渐趋于原点, 系统是渐近稳定的。图 7显示了观测器的状态轨迹, 从图 7可以看出, 观测器的状态由初始值[0, 0]逐渐逼近系统实际状态, 且最终趋于稳定。图 8显示了观测器误差的状态轨迹, 在初始时刻, 针对状态不可测现象, 令观测器状态和系统实际状态初始值不同, 因此观测器误差较大, 随着系统的运行, 误差可以迅速减小并趋于0。

4 结束语

本文提出一种基于观测器的动态事件触发机制, 根据2个LMIs建立系统渐近稳定的条件。通过引入额外的内部动态变量, 事件触发条件会更加多样化, 从而减少事件触发次数。本文给出了Zeno行为不存在的证明过程, 并通过仿真实例论证结果, 这些实例可应用于线性时不变系统。下一步可以考虑改善事件触发条件和加入优化控制, 以期达到优化系统性能指标的目的。