b. 中国科学技术大学 计算机科学与技术学院, 合肥 230026
b. School of Computer Science and Technology, University of Science and Technology of China, Hefei 230026, China
智能合约是一种无需中介、自我验证、自动执行合约条款的计算机交易协议, 近年来随着区块链技术的日益普及而备受关注。区块链技术去中心化和数据防篡改等特性, 解决了智能合约的信任问题, 因此使得智能合约更适合在区块链上进行实现。智能合约[1-3]作为一种能自动执行合约条款的计算机程序, 需要尽量避免语法和语义错误, 并且对于正确性及其他属性具有较高要求, 以保证用户的财产安全。由于现有通过专家审计和人工复查生成可信合约代码的方法很难确保代码的绝对安全, 因此导致智能合约存在安全隐患。2016年, 恶意攻击者通过以太坊Solidity[4]语言中的递归调用漏洞对运行在以太坊公有链上的The DAO[2-3]智能合约进行攻击, 导致360万以太币被盗。2017年, 以太坊Parity电子钱包因多重签名漏洞导致数亿美元资金遭到冻结[5]。2018年, 黑客利用ERC-20标准代币合约整数溢出漏洞攻击了美链BEC的智能合约, 导致BEC货币急剧贬值, 价值几乎归零。同年, BAI和EDU智能合约出现重大漏洞, 其代币(token)可被随意转走。可见, 智能合约已成为区块链应用安全的重灾区, 但是到目前为止能够对智能合约漏洞进行完备性和安全性分析的方法仍未被提出, 当前对于智能合约的安全保障主要依靠专家审计和人工复查, 然而该方式不能保证代码的绝对安全。
形式化方法[6]的本质是基于数学的方法来描述目标软件系统属性的一种技术, 适用于计算机软硬件系统的规范、开发和验证。形式化验证[7]是使用基于数学变换的静态分析方法来确定程序规范和代码行为, 如从协议规约出发验证程序的安全属性等, 其是目前安全级别最高的一种验证方法。为对智能合约漏洞进行分析与研究, 本文提出一种针对智能合约整数溢出漏洞的形式化建模与验证方法, 先对合约代码进行建模分析, 再利用形式化验证方法解决建模过程中的无限状态问题。
1 相关研究 1.1 智能合约概念智能合约概念由跨领域法律学者尼克·萨博于1995年提出, 智能合约是一套以数字形式定义的承诺, 包括合约参与方可以在上面执行这些承诺的协议[8]。然而, 受限于可编程的合约数字系统, 智能合约并未在当时得到具体应用。中本聪于2008年底在比特币[9]系统中提出了区块链概念。区块链技术去中心化、防篡改、可编程和高可用等特性, 解决了智能合约的信任问题。BUTERIN于2013年底发表《以太坊:下一代智能合约和去中心化应用平台》一文[10], 致力于将以太坊打造成最佳智能合约平台, 通过将智能合约与区块链技术进行融合, 拓宽区块链技术的应用领域。可见, 以太坊已成为主流的智能合约开发和运行平台。
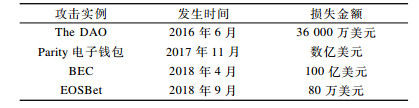
1.2 智能合约安全问题智能合约是部署在区块链系统上的有状态的链上代码。由于执行代码不能保证绝对安全, 因此造成智能合约容易受到黑客攻击。表 1给出了4种智能合约漏洞引发的攻击实例。智能合约除了面临软件安全性和可信性问题外, 还存在以下问题:1)智能合约的不可篡改性使其一旦被部署上线, 便无法进行修改; 2)智能合约的源码公开导致其被恶意攻击的成本大幅降低; 3)智能合约在代码开发过程中存在的Bug容易产生智能合约漏洞。由此可见, 智能合约需要一种安全高效的审计方式来保障其安全性。
|
下载CSV 表 1 智能合约攻击实例 Table 1 Attack examples of smart contract |
为解决智能合约中存在的安全问题, 本文引入形式化方法。形式化方法通常运用数学归纳法验证目标的完备性和安全性, 主要包括:
1) 基于类BAN逻辑的形式化方法[11]。该方法本质上是基于知识和信念推理的模态逻辑分析方法, 其从事先定义的公理出发, 通过一系列推理公理推证协议满足安全性, 但不能确保验证结果的可靠性。
2) 基于模型检验的形式化方法[12]。该方法是分析有穷状态系统正确性的重要方法。BOREALE提出基于符号化模型检验的形式化方法[13], 该方法的基本思想是推迟实例化, 在只进行值的匹配或比较时, 才对变量进行实例化。符号化方法可以缓解攻击者生成无穷多个消息导致的状态组合爆炸问题。现有的智能合约形式化验证工作主要使用该方法对合约进行检验[14-15], 但是其不能验证智能合约的完备性。
3) 基于密码学原语代数属性的形式化方法。该方法能对含有代数运算算子的协议或者合约进行形式化验证, 如文献[16]给出了能对含有异或算子的一类无穷会话并发协议完成验证的方法。
4) 基于定理证明的形式化方法。该方法将协议形式化描述为一系列逻辑子句, 并通过归纳证明[17]和Applied Pi演算[18-19]等方式验证其相应的安全属性是得到满足还是遭到破坏, 该方法的主流验证工具包括Tamarin、ProVerif等, 但是上述验证工具在验证过程中均需要人工辅助, 且学习成本较高。SmartVerif[20]是一款支持全自动形式化验证的工具。本文使用基于定理证明的SmartVerif形式化验证工具对模型进行验证。
2 形式化建模与验证方法设计为对代币智能合约进行形式化验证, 需先对程序的一系列逻辑代码进行建模, 再通过演算证明其相应的安全属性是得到满足还是遭到破坏, 但由于目前智能合约的形式化验证只针对单个协议进行建模, 因此无法对某类漏洞合约进行建模, 如整数溢出漏洞, 并且因为智能合约没有固定的主函数入口, 每个外部可见的函数都可被任意用户进行任意多次调用, 所以建模后得到的模型状态空间为无限大, 验证时无法对所有情况进行遍历。针对以上问题, 本文设计一种基于数学归纳法的形式化建模与验证方法。
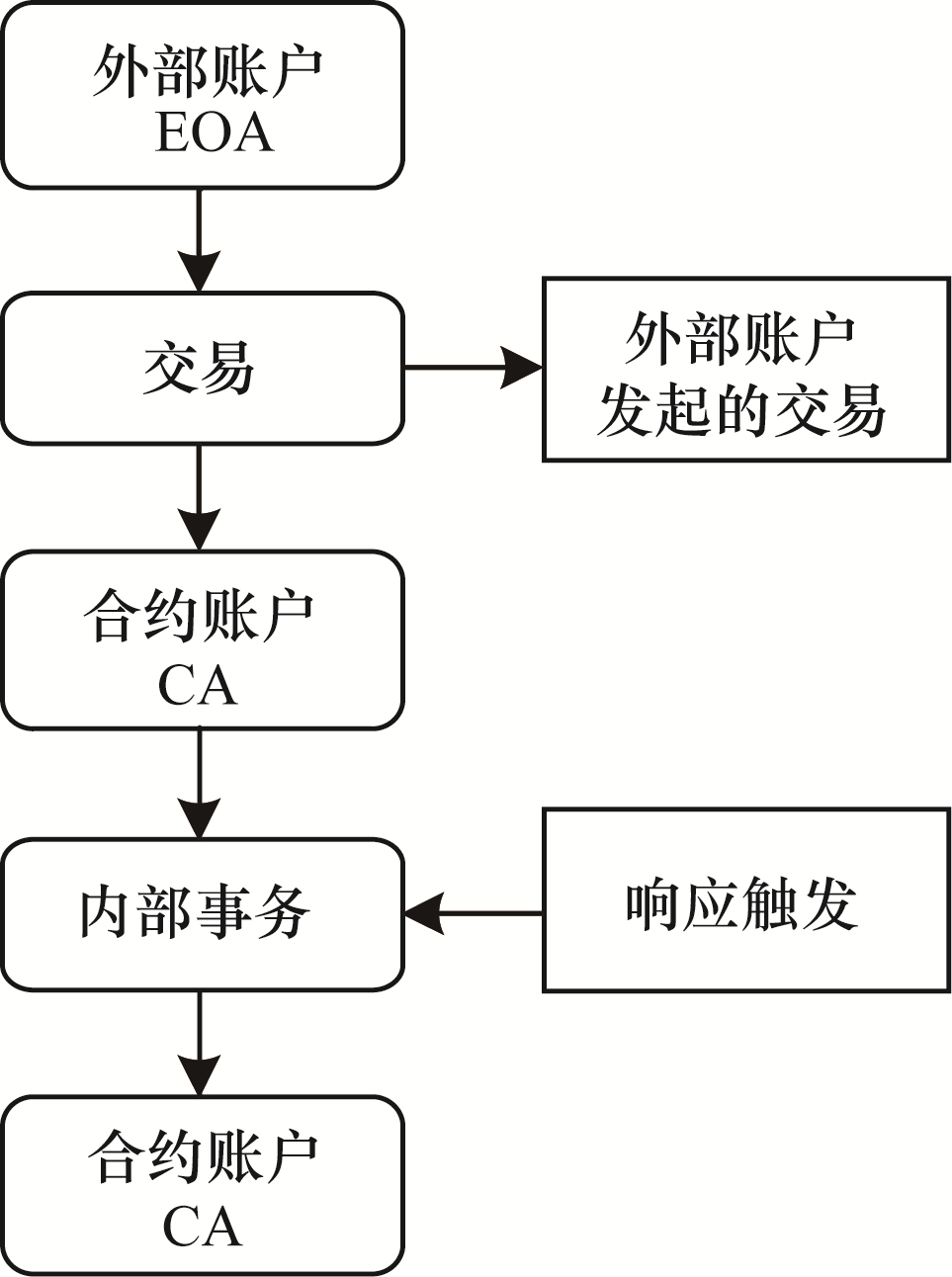
2.1 模型角色 2.1.1 不诚实的用户在以太坊中有外部账户(Externally Owned Accounts, EOA)和合约账户(Contract Accounts, CA)两种不同类型的账户, 其共用一个地址空间, 如图 1所示。外部账户由公钥-私钥对控制, 即被分配给用户, 其地址由公钥决定。合约账户由存储在账户中的代码控制, 其地址在创建合约时确定。

|
Download:
|
| 图 1 外部账户与合约账户 Fig. 1 EOA and CA | |
以太坊中的账户包括随机数(nonce)、账户余额(balance)、合约代码(codeHash)和存储(storageRoot)4个字段, 其中只有合约账户才有代码且存储codeHash, 即该账户的以太坊虚拟机代码的哈希值, 并且由于codeHash在生成后不可修改, 因此意味着智能合约代码也不可修改。外部账户可以触发交易, 而合约账户不能主动发起交易, 只能在被触发后按预先编写的智能合约代码执行, 其交易流程如图 2所示。
|
Download:
|
| 图 2 外部账户与合约账户的交易流程 Fig. 2 Transaction process of EOA and CA | |
由于不诚实用户可能是外部账户也可能是合约账户, 因此本文构建的模型角色需要包含两个账户的功能。若不诚实的用户是外部账户, 则其恶意构造函数会使转账逻辑中产生整数溢出漏洞, 导致代币的任意转账或无限增发。若不诚实的用户是合约账户, 则其会通过直接实现某段恶意代码并等待智能合约转账, 从而触发合约代码。当调用外部合约或指定合约进行外部调用时, 若此时外部调用被攻击者劫持, 则合约会执行恶意代码, 包括利用fallback函数回调, 其等同于代码重入攻击, The DAO事件就是典型的重入攻击实例。
2.1.2 合约自身及合约拥有者因为合约中存在一些函数只有合约拥有者才能调用执行, 所以模型建立时要有合约拥有者才能进行后续建模。因此, 本文需要对合约的拥有者进行模型构建, 满足合约中函数的正常调用执行。
2.2 建模属性智能合约具有独立运行、不可篡改等特性。由于开发者可以自定义智能合约的交易逻辑并将其代码发布在区块链上, 因此智能合约无法避免地存在与传统程序类似的安全漏洞, 但不同的是智能合约代码运行于开放的区块链网络且可被任意调用, 合约执行后具有不可篡改的特性, 因此若有不诚实的用户利用了合约漏洞, 则会造成更大的危害。
本文主要针对智能合约的整数溢出漏洞进行研究。整数溢出漏洞是一种常见的高危漏洞。因为计算机中整型变量存在上下界, 所以如果在算术运算中结果超出其上下界, 即整型变量最大或者最小表示范围, 则虚拟机会自动截断高位, 导致运算结果异常。典型的智能合约整数溢出漏洞事件有BEC、SMT、EDU和BAI等, 恶意攻击者通过构造参数绕过合约中的检测语句, 使得转账逻辑中产生了整数溢出, 导致代币无限增发或任意转账。产生整数溢出漏洞的主要原因为直接通过简单的加减乘除等数值运算操作, 而未使用assert或require语句以保证运算不产生整数溢出。
本文通过对BEC、SMT等漏洞事件的观察, 发现不诚实的用户利用整数溢出漏洞攻击代币智能合约的主要目的是非法修改账户余额获利, 因此本文定义安全属性
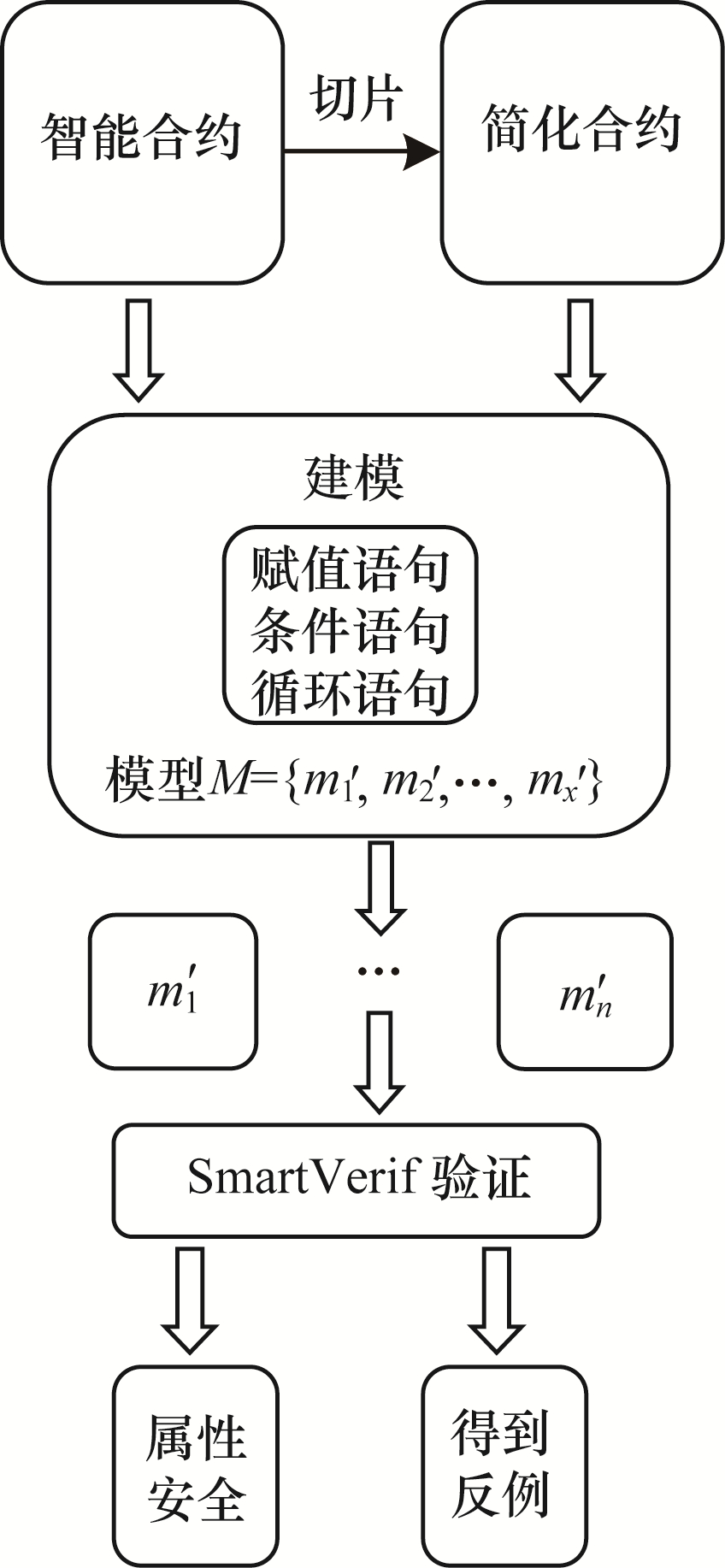
对于一个给定的智能合约C, 本文提出一个将智能合约转化为形式化模型的通用方法并对其进行验证。智能合约的建模与验证流程如图 3所示。
|
Download:
|
| 图 3 智能合约的建模与验证流程 Fig. 3 Modeling and verification process of smart contract | |
程序切片是对程序进行理解和分析的常用技术。考虑到直接利用合约进行建模得到的模型状态空间过大, 不便于后续验证。因此, 本文根据智能合约C={f1, f2, …, fx}和安全属性φ生成切片准则, 在对合约进行切片后得到简化合约C={f1′, f2′, …, fx′}。
2.3.2 建模本文建模后得到的模型为M={m1′, m2′, …, mx′}, 使用基于定理证明的SmartVerif形式化验证工具对其进行验证。根据SmartVerif的建模要求, 需要引入多重集合重写规则。多重集合重写规则为m1′三元组, 记为l-[a]→r, 其中, l代表一组前提或假设, a代表待选的动作或者行为, [a]表示动作a的集合, r代表假设成立并采取动作a后产生的结果。
本文主要的建模过程是将智能合约的各类语句转换为多重集合重写规则:
1) 对于赋值语句, 由于SmartVerif的模型语言暂不支持全局变量, 为能对合约进行建模, 因此本文引入全局变量约束, 具体如下:
1.restriction set_in:
2.“All x y #t3.Exist(x, y)@t3==>
3.(Ex #t2.Store(x, y)@t2 & #t2 < #t3
4. & (All #t1.Del(x)@t1==> (#t1 < #t2 | #t3 < #t1))
5. & (All #t1 yp.Store(x, yp)@t1==> (#t1 < #t2\\#t1=#t2 | #t3 < #t1))
6.)”
7.restriction set_notin:
8.“All x #t3.NotExist(x)@t3 ==>
9.(All #t1 y.Store (x, y) @t1 ==> #t3 < #t1)
10.(Ex #t1.Del(x)@t1 & #t1 < #t3
11. & (All #t2 y.Store(x, y)@t2 & #t2 < #t3 ==> #tw < #t1))”
在全局变量约束中, Store(x, y)事件表示全局变量的赋值操作, Del(x)事件表示对全局变量做清空操作, Exist(x, y)表示获取全局变量x的y值, Set_in约束表示Exist(x, y)操作获得的y值需满足以下条件:
(1) 在Exist(x, y)操作前存在给x赋值的Store(x, y)事件。
(2) 该Store(x, y)事件和Exist(x, y)事件之间不存在Del(x)事件。
(3) 该Store(x, y)事件是距Exist(x, y)事件时间最近的一个Store(x, y)事件。
Set_notin约束与Set_in约束相反。在引入上述约束条件后, 即可对全局变量进行建模。
2) 对于条件语句, 由于SmartVerif的模型语言没有实现数值比较的相关约束, 因此本文引入数值比较约束, 具体如下:
1.restriction predicate l:
2.“All #i a b.Pred_not_equals (a, b)@i==>not((a=b))”
3.restriction predicate 2:
4.“All #i a b.Pred_equals (a, b)@i==>(a=b)”
5.restriction predicate 3:
6.“All #i a b.Pred_not_Bigger(a, b)@i==>not(Ex c.(a=(b)+(c)))”
7.restriction predicate 4:
8.“All #i a b.Pred_Bigger (a, b)@i==>(Exc.(a=(b)+(c)))”
以predicate 4为例, 当Pred_Bigger(a, b)事件发生时, 一定存在a=b+c, 其他约束也与此类似。
3) 对于循环语句, 本文只处理有界循环, 将其展开为条件语句和赋值语句的集合。
2.3.3 验证因为智能合约没有固定的主函数入口, 每个外部可见的函数都可被任意用户进行任意多次调用, 所以建模后得到的模型状态空间为无限大, 验证时无法对所有情况进行遍历。本文借鉴数学归纳法的思想优化模型验证过程:对于每个函数, 假设其安全属性φ在运行前成立, 并通过验证工具判断其在验证后是否成立。如果成立, 则该函数的安全属性得到证明, 即此函数不存在溢出漏洞; 反之, 则证明此函数存在溢出漏洞, 并可以得到反例。智能合约的抽象过程表示为:
1.while true
2.(user, func, args):= // arbitrary
3.run func (args) as user
3 实验结果与分析 3.1 整数溢出漏洞分析通过对代币合约FountainToken进行建模分析后, 找出以下代码中的第12行和第14行为整数溢出漏洞:
1.function batchTransfers (address[] receivers, uint256[] amounts) {
2.uint receiveLegth = receivers.length;
3.requuire (receiveLength == amounts.length);
4.unit receiverCount = 0;
5.unit256 totalAmount = 0;
6.unit i;
7.address r;
8.for(i=0;i < receiveLength; i++) {
9.r=receivers[i];
10.if (r==address(0) || r==owner) continue;
11.receiverCount++;
12.totalAmount+=amounts[i];
13.}
14.require(totalAmount >0);
15.require(canPay(msg.sender, totalAmount)):
16.wallets[msg.sender]-=totalAmount;
17.unit256 amount;
18.for (i = 0; i < receiveLength; i++) {
19.r=receivers[i];
20.if (r==address(0) || r==owner) continue;
21.amount = amounts[i];
22.if (amout == 0) continue;
23.wallets[r]=wallets[r].add(amount);
24.emit Transfer (msg.sender, r, amount);
25.}
26.return true;
27.}
分析发现:由于该溢出漏洞的攻击发生条件是amounts数组中的元素存在极大值, receivers数组中的地址账户余额为极小值, 因此totalAmount在累加过程中会发生上溢出, 最终wallets[msg.sender]只减少极小值, 而receivers数组中某一地址r的wallets[r]余额增加为极大值, 使得合约不具备本文定义的安全属性φ。本文共对5个存在整数溢出漏洞的代币智能合约进行建模与验证, 成功找出了其中的溢出漏洞, 如表 2所示。

|
下载CSV 表 2 代币智能合约的整数溢出漏洞 Table 2 Integer overflow vulnerabilities of token smart contract |
本文提出的代币智能合约形式化建模与验证方法同样适用于其他类型的合约漏洞。以The DAO攻击为例验证该建模方法对重入漏洞的有效性, 发现不诚实的用户利用重入漏洞攻击代币智能合约的主要目的是从账户中非法重复提取代币, 因此本文定义了安全属性φ2:balanceu+etheru=balanceu′+etheru′, 其中, u表示任意账户, balanceu表示u的代币余额, etheru表示u的以太币余额, balanceu′和etheru′表示任意一次交易后的两类余额。通过验证该属性可以发现当合约存在重入漏洞时, 一定存在某次交易使得该安全属性不成立。由此得出, 本文提出的形式化建模与验证方法对智能合约的漏洞检测具有通用性。
4 结束语随着智能合约应用的快速增长, 其频发的安全事件严重威胁大众经济财产安全。针对代币智能合约的安全问题, 本文提出一种形式化建模与验证方法。使用切片技术和基于数学归纳法的形式化验证方法, 解决了状态空间爆炸和函数无限调用问题。对5个存在整数溢出漏洞的代币智能合约和The DAO攻击进行形式化建模与验证实验, 结果表明本文方法能成功找出代币智能合约漏洞。下一步可将研究范围扩展至更多的智能合约及漏洞类型, 通过归纳总结不同类型的漏洞得到其特有的安全属性, 从而实现智能合约的形式化建模与验证。
| [1] |
SZABO N. Formalizing and securing relationships on public networks[J]. First Monday, 1997, 2(9): 1-19. |
| [2] |
MEHAR M I, SHIER C L, GIAMBATTISTA A, et al. Understanding a revolutionary and flawed grand experiment in blockchain[J]. Journal of Cases on Information Technology, 2019, 21(1): 19-32. |
| [3] |
WU Xuchuan, LIU Xue. Analysis and thinking of The DAO attack[J]. Financial Perspectives Journal, 2016(7): 19-24. (in Chinese) 伍旭川, 刘学. The DAO被攻击事件分析与思考[J]. 金融纵横, 2016(7): 19-24. |
| [4] |
Solidity documentation[EB/OL].[2019-11-20].https://solidity.readthedoc.io.
|
| [5] |
BOCEK T, STILLER B.Smart contracts-blockchains in the wings[M]//LINNHOFF-POPIEN C, SCHNEIDER R, ZADDACH M.Digital marketplaces unleashed.Berlin, Germany: Springer, 2017: 169-184.
|
| [6] |
Formal methods[EB/OL].[2019-11-20].http://en.wikipedia.orgi/Formal_methods.
|
| [7] |
ZAKI M H, TAHAR S, BOIS G. Formal verification of analog and mixed signal designs:a survey[J]. Microelectronics Journal, 2008, 39(12): 1395-1404. DOI:10.1016/j.mejo.2008.05.013 |
| [8] |
MA Ang, PAN Xiao, WU Lei, et al. A survey of the basic technology and application of block chain[J]. Journal of Information Security Research, 2017, 3(11): 968-980. (in Chinese) 马昂, 潘晓, 吴雷, 等. 区块链技术基础及应用研究综述[J]. 信息安全研究, 2017, 3(11): 968-980. |
| [9] |
BERENTSEN A.Aleksander Berentsen recommends "bitcoin: a peer-to-peer electronic cash system" by Satoshi Nakamoto[M]//FREY B S, SCHALTEGGER C A.21st century economics.Berlin, Germany: Springer, 2019: 7-8.
|
| [10] |
BUTERIN V.A next-generation smart contract and decentralized application platform[EB/OL].[2019-11-20].https://www.mendeley.com/catalogue/7f15213c-fdfa-3247-8f64-5997b917c898/.
|
| [11] |
BURROWS M, ABADI M, NEEDHAM R. A logic of authentication[J]. ACM SIGOPS Operating Systems Review, 1989, 23(5): 1-13. DOI:10.1145/74851.74852 |
| [12] |
MAJUMDAR R. Paul Ammann and Jeff Offutt introduction to software testing[J]. The Computer Journal, 2010, 53(5): 615-616. |
| [13] |
BAUDET M.Deciding security of protocols against off-line guessing attacks[C]//Proceedings of the 12th Conference on Computer and Communication Security.New York, USA: ACM Press, 2005: 16-25.
|
| [14] |
HU Kai, BAI Xiaomin, GAO Lingchao, et al. Formal verification method of smart contract[J]. Journal of Information Security Research, 2016, 2(12): 1080-1089. (in Chinese) 胡凯, 白晓敏, 高灵超, 等. 智能合约的形式化验证方法[J]. 信息安全研究, 2016, 2(12): 1080-1089. |
| [15] |
BHARGAVAN K, SWAMY N, ZANELLA-BÉGUELIN S, et al.Formal verification of smart contracts[C]//Proceedings of 2016 ACM Workshop on Programming Languages and Analysis for Security.New York, USA: ACM Press, 2016: 1-10.
|
| [16] |
BLANCHET B. A computationally sound mechanized prover for security protocols[J]. IEEE Transactions on Dependable and Secure Computing, 2008, 5(4): 193-207. DOI:10.1109/TDSC.2007.1005 |
| [17] |
PAULSON L C. The inductive approach to verifying cryptographic protocols[J]. Journal of Computer Security, 1998, 6(1/2): 85-128. |
| [18] |
ABADI M, FOURNET C.Mobile values, new names, and secure communication[C]//Proceedings of the 28th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages.New York, USA: ACM Press, 2001: 1-13.
|
| [19] |
ABADI M, CORTIER V. Deciding knowledge in security protocols under equational theories[J]. Theoretical Computer Science, 2006, 367(1/2): 2-32. |
| [20] |
XIONG Yan, SU Cheng, HUANG Wenchao, et al.SmartVerif: push the limit of automation capability of verifying security protocols by dynamic strategies[C]//Proceedings of the 29th USENIX Security Symposium.Boston, USA: USENIX Association, 2020: 1-5.
|
 2020, Vol. 46
2020, Vol. 46
