0 概述

在未来空战中, 无人机(Unmanned Aerial Vehicle, UAV)集群作战将是重要的作战形式之一, 针对其高动态、网络拓扑结构多变等特性, 采用分布式网络结构可提高无人机集群网络的抗毁性。此外, 实现信息安全、可靠传输是其完成任务的关键, 确保无人机之间的可靠通信, 将成为一项重要的研究内容^[1]。

近年来, 如何有效对抗智能性干扰与提高通信安全已成为研究热点^[1]。在抗干扰技术研究中, 认知抗干扰算法已成为研究热点方向之一^[2], 该算法可归纳为如下两类:一类是基于强化学习理论^[3]进行可用信道的选择, 主动规避干扰信道, 从而实现频域抗干扰。文献[4]提出基于协作Q学习(Q-Learning, QL)的信道选择算法, 该算法可提高数据传输成功率, 但当状态空间规模较大时, 其面临维数灾难的问题^[5-6]。针对该问题, 文献[7]提出将深度Q网络(DQN)在线学习算法应用于信道选择。当信道数量较多时, 文献[8-9]利用演员-评论家(Actor-Critic, AC)算法进行信道选择, 但是该算法存在方差较大以及稳定性较差的问题。另一类是基于博弈论的方法^[10-12], 根据敌我双方的竞争关系, 建立功率域抗干扰博弈模型, 通过求解博弈均衡得到最佳传输功率, 实现从功率上压制干扰信号以达到抗干扰的目的。以上算法均是仅从单个频域或者功率域角度考虑, 针对智能性干扰攻击的灵活性较差^[13]。

为提高网络抗智能干扰的能力, 本文将功率域和频域抗干扰方法相结合, 基于优势演员-评论家(Advantage Actor-Critic, A2C)^[14]与Stackelberg博弈(Stackelberg Game, SG), 提出一种多域联合认知抗干扰(Multiple Domain Joint Cognitive Anti-Jamming, MDJC-AJ)算法。该算法将可用信道探索问题转化为序贯决策问题, 由感知到的环境频谱状态进行信道选择。根据设定的干扰容忍双阈值将信道干扰程度分为严重、中度与轻微3个等级, 并对处于中度干扰等级的信道建立功率域斯塔克伯格博弈模型, 通过求解博弈均衡得到最佳传输功率。与此同时, 本文采用簇头协助决策方式来协助簇内信道决策成功率较低的节点, 以提高网络整体感知环境的准确性与干扰信道决策成功率。

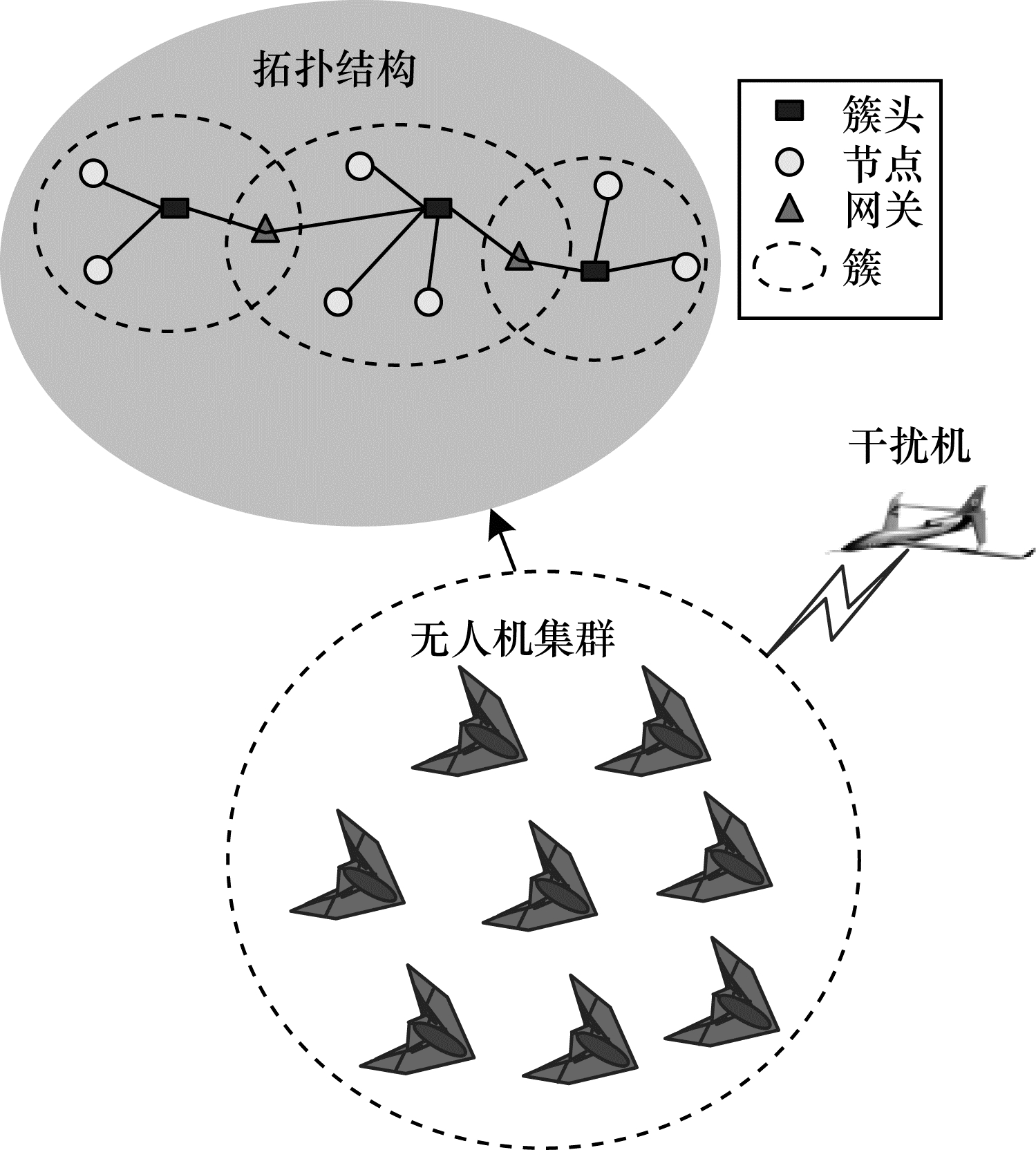
1 无人机集群网络模型

无人机集群网络采用层次结构的移动Ad-Hoc网络, 当无人机的数量大于6架时, 适合采用分层式结构^[15]。无人机集群网络对抗智能干扰机示意图如图 1所示。

假设网络中干扰机为J, 干扰机个数为1, 节点总数为N_S, 分簇数M=N_S/N_C, N_C为簇内节点个数, 节点i的簇内邻节点个数C_-i⊂Ω_S, 其中, Ω_S为网络节点集合。假设簇头具有较高的等级, 数据处理能力最强, 其在簇内则充当局部控制中心的角色, 簇间节点通过所在簇的簇头转发数据进行通信。

2 多域联合认知抗干扰算法 2.1 基于A2C的频域抗干扰算法

信道选择过程可建模为马尔可夫决策过程^[16], 由四元组(S, A, R, λ)来描述, 其中, S为状态空间, A为动作空间, 累计奖励函数$R = \sum\limits_{t = 1}^T {{\lambda ^{t - 1}}} {R_t}, \lambda \in [0, 1]$为有损因子, R_t为t时刻得到的即时奖励。马尔可夫决策过程是序贯决策问题, 其最终目标是找到最优决策序列π(s, a):S×A→ ${\mathbb{R}}_+ $, 以得到最大期望奖励Q^*(s, a), 即给定状态s∈S和动作a∈A下, 选择最优策略π(s, a)获得最大期望奖励Q^*(s, a)=max_πQ^π(s, a)=E[R_t|s_t=s, a_t=a]。信道选择的最终目标是根据感知环境干扰状况得到最有效的抗干扰策略, 将信道选择问题转化为序贯决策问题, 需要设定信道选择过程对应的奖励函数、状态空间以及动作空间。

2.1.1 奖励函数

在t时刻, 且无干扰机时, 节点i接收信号的信干噪比(Signal to Interference-plus Noise Ratio, SINR)为γ_NJ(t), 存在干扰机时, SINR为γ_YJ(t), 可表示为:

$ {{\gamma _{NJ}}(t) = \frac{{g_S^iP_S^i(t)}}{{P_S^{ - i}(t) + \varepsilon }}} $

(1)

$ {{\gamma _{YJ}}(t) = \frac{{g_S^i(t)P_S^i(t)}}{{{g_J}(t){P_J}(t) + P_S^{ - i}(t) + \varepsilon }}} $

(2)

其中, P_Sⁱ(t)为节点i的传输功率, P_J(t)为干扰机J的干扰功率, g_Sⁱ(t)、g_J分别为节点i和干扰机J的信道增益, $P_s^{ - i}(t) = \sum\limits_{j \ne i} {g_s^j} P_s^j(t)$为网络中不包含节点i的其他邻居节点对节点i的干扰功率总和, ε为高斯加性白噪声。

假设网络通信总带宽为W, 将其均分为K个子信道b, 则有$\sum\limits_{k = 1}^K {{b_k}} = W$。在无干扰机的情况下, 在时间步Δt内, 节点i的信息传输速率如式(3)所示, 存在干扰机的情况下, 节点i的信息传输速率如式(4)所示:

$ {{r_S}(t) = {{\tilde b}_k}(t){\rm{lb}}(1 + {\gamma _{NJ}}(t))} $

(3)

$ {r_J^i(t) = {{\tilde b}_k}(t){\rm{lb}}(1 + {\gamma _{YJ}}(t))} $

(4)

其中, ${{\tilde b}_k}(t)$为t时刻的通信信道。

抗干扰通信的目标是确保信息安全以及可靠传输, 将即时奖励R_t定义为通信安全容量C_sec^i[17], 可表示为:

$ C_{{\rm{sec}}}^i = {[r_S^i(t) - r_J^i(t)]^ + } $

(5)

其中, [·]⁺=max{0, ·}, 即时奖励R_t=C_secⁱ。

2.1.2 状态空间与动作空间

假设环境状态空间S为节点i的前一时刻感知频谱 b_t－1, 则时刻t的状态s_t可表示为:

$ {s_t} = {\mathit{\boldsymbol{b}}_{t - 1}},{s_t} \in S $

(6)

节点根据观测状态s_t和即时奖励R_t进行信道选择, 将动作空间定义为可选信道, 则有A={1, 2, …, K}, 且其对应于信道索引。信道选择过程可描述为:在t时刻, 节点由状态s_t选择信道a_t=k∈A, 并获得即时奖励C_secⁱ。

2.1.3 基于优势演员-评论家的频域抗干扰算法

AC算法是由行动者(Actor)与评论家(Critic)组成的强化学习算法, 其中, Actor负责更新策略, Critic负责更新动作值函数。与AC算法相比, A2C算法通过引入基线能够降低学习过程中的方差, 以较准确的动作值指导策略更新, 可带来更好的求解效果。在实际应用中真实价值很难得到, 一般采用函数近似法对价值和动作函数进行参数化, 利用神经网络等机器学习算法求解, 求解过程如下:

1) 对于Critic而言, 其目标是通过不断地更新参数θ, 使得值函数V_θ(s)更加逼近真实的累计奖励值C_secⁱ(s), 即:

$ {\theta ^*} = \mathop {{\rm{ argmin }}}\limits_\theta \left\{ {\frac{1}{2}{{(C_{{\rm{sec}}}^i + \lambda C_{{\rm{sec}}}^i({s^\prime }) - {V_\theta }(s))}^2}} \right\} $

(7)

2) 对于Actor而言, 其目标是通过不断地更新参数w, 使得其尽可能得到好的策略π_w(s, a), 即:

$ {w^*} = \mathop {{\rm{ argmax }}}\limits_w \left\{ {\sum\limits_{s \in S} d (s)\sum\limits_{a \in A} {{\pi _w}} (s,a)C_{{\rm{sec}}}^i(s)} \right\} $

(8)

其中, d(s)对应起始状态s。

3) 在每一步更新中, Actor根据当前状态s和策略π_w(s, a), 执行动作a并转到下一状态s′, 得到即时奖励C_secⁱ。Critic根据真实奖励和之前标准下的评分C_secⁱ+λC_secⁱ(s′)来修正评价标准, 使得估计价值更加逼近真实奖励值。

为增加模型探索能力, 在模型目标函数中加入策略的熵正则化项, 其可衡量概率策略分布的不确定性, 且其值越大说明模型具有更好的多样性^[18-19]。Actor网络的参数w基于策略梯度下降的计算方法为:

$ \begin{array}{l} w \leftarrow w + \alpha \sum\limits_t {{\nabla _w}} {\rm{lb}} {\pi _w}(s,a)\underbrace {(C_{{\rm{sec}}}^i(s) - {V_\theta }(s))}_{{\rm{优势函数的估计}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \eta {E_s}[{\nabla _w}{H^\pi }(s)] \end{array} $

(9)

其中, ${H^\pi }(s) = - \sum\limits_a {{\pi _w}} (s, a){\rm{ lb }}\pi (s, a)$为策略梯度的熵, E[·]为期望, η为策略梯度的熵在目标函数中的权重, α、β分别为Actor和Critic网络学习率, 值网络模型目标函数梯度为:

$ \theta \leftarrow \theta + \beta \sum\limits_t \partial \left[ {\frac{1}{2}{{(C_{{\rm{sec}}}^i(s) - {V_\theta }(s))}^2}} \right]/\partial \theta $

(10)

通过A2C算法决策出各信道干扰情况后, 根据给定信道干扰容忍双阈值P_Jth1^sec与P_Jth2^sec将干扰功率划分为严重、中度与轻微3个等级, 信道干扰等级判定规则如表 1所示。

2.2 基于SG的功率域抗干扰算法

在2.1节的基础上, 当上一时刻所用信道在当前时刻被判决为等级2时, 则对该信道建立功率域SG模型, 并通过求解Stackelberg均衡(Stackelberg Equilibrium, SE)得到最佳传输功率, 实现功率域抗干扰。

假设网络中的节点为领导者, 干扰机为跟随者, 参与者的行动受功率约束。定义博弈模型为G_{s, j}=〈{Ω_S, J}, {P_S, P_J}, {U_S, U_J}〉, 其中, P_S和P_J分别为节点和干扰机的传输功率, U_S与U_J分别为节点与干扰机的效用函数。以节点作为领导者, 并假定其可精确估计出干扰功率, 而干扰机对节点的功率估计存在观测误差^[10], 且观测误差为$e = \left| {\hat P_s^i - P_s^i} \right|/P_s^i, \hat P_s^i$为干扰机观测的节点i的功率。根据式(2)得到的接收信号SINR, 并考虑节点间的通信开销, 则节点i的效用函数可表示为:

$ U_S^i(P_S^i,P_S^{ - i},{P_J}) = {\gamma _{YJ}} - L_S^iP_S^i $

(11)

其中, L_SⁱP_Sⁱ为节点i的通信代价。

干扰机J的效用函数可表示为:

$ {U_J}(P_S^i,P_S^{ - i},{P_J}) = - {\hat \gamma _{YJ}} + L_S^i\hat P_S^i - {L_J}{P_J} $

(12)

其中, L_JP_J为干扰代价, ${{\hat \gamma }_{YJ}}$为γ_YJ的观测值。

求解SE是博弈理论的重要内容。当处于SE状态时, 节点可得到保证本身损失最小的传输功率, 而干扰机可得到最佳的干扰功率。本文利用逆向归纳法求解SE, 并定义功率约束下的SE为(P_S^SE, P_J^SE), 且P_S^SE、P_J^SE分别表示为:

$ {P_S^{{\rm{SE}}} = \mathop {{\rm{ arg}}{\kern 1pt} {\rm{max }}}\limits_{0 \le {P_S} \le P_S^{{\rm{Max}}}} {U_S}(P_S^i,P_S^{ - i},{P_J})} $

(13)

$ {P_J^{{\rm{SE}}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{max}}}\limits_{0 \le {P_J} \le P_J^{{\rm{Max}}}} {U_J}(\hat P_S^i,\hat P_S^{ - i},{P_J})} $

(14)

其中, P_S^Max、P_J^Max分别为节点最大传输功率与干扰机最大干扰功率, P_S^SE、P_J^SE分别为节点最佳传输功率与干扰机最佳干扰功率。

P_J^SE的求解过程如下:

1) 考虑一般情况, 基于式(12), ${U_J}\left( {\hat P_s^i, \hat P_s^{ - i}, {P_J}} \right)$关于P_J的一阶导数为${\rm{d}}{U_J}/{\rm{d}}{P_J} = g_s^i{g_J}\hat P_s^i/\left( {\hat P_s^{ - i} + } \right.{\left. {\varepsilon + {g_J}{P_J}} \right)^2} - {L_J}$, 二阶导数为${{\rm{d}}^2}{U_J}/{\rm{d}}P_J^2 \le 0$, 则${U_J}\left( {\hat P_s^i} \right., \left. {\hat P_s^{ - i}, {P_J}} \right)$关于P_J为凹函数。令一阶导数等于0, 得到U_J^Max, 对应$P_J^{{\rm{SE}}} = {{\hat P}_J} = \left( {\sqrt {g_S^i{g_J}\hat P_s^i/{L_J}} - \varepsilon - \hat P_s^{ - i}} \right)/{g_J}$, 其中, ${{\hat P}_J} \in \left( {0, P_J^{{\rm{Max}}}} \right)$。

2) 考虑极端情况, 有以下2种情况:

(1) 相比阻断节点间的信息传输, 干扰机本身的损失更低, 此时干扰机的P_J^SE=P_J^Max。

(2) 相比阻断节点间的信息传输, 干扰机本身的损失更大, 此时P_J^SE=0, 则求得P_J^SE为:

$ P_J^{{\rm{SE}}} = \left\{ {\begin{array}{*{20}{l}} {0,\hat P_S^i \le {L_J}(\hat P_S^{ - i} + {\varepsilon ^2})/(g_S^i{g_J})}\\ {P_J^{{\rm{Max}}},\hat P_S^i \ge {L_J}{{(P_J^{{\rm{Max}}}{g_J} + \hat P_S^{ - i} + \varepsilon )}^2}/(g_S^i{g_J})}\\ {{{\hat P}_J} = \left( {\sqrt {g_S^i{g_J}P_S^i/{L_J}} - \varepsilon - \hat P_S^{ - i}} \right)/{g_J},{\rm{ 其他 }}} \end{array}} \right. $

(15)

P_S^SE的求解过程如下:

假设对节点i而言, 其认为干扰机的观测不存在误差, 即$\hat P_s^i = P_s^i$, 将式(15)代入式(11), 则有:

$ \begin{array}{l} {U_S}\left( {P_S^i,P_S^{ - i},{P_J}} \right) = \\ \left\{ \begin{array}{l} \frac{{g_S^i}}{{\left( {\varepsilon + P_S^{ - i}} \right)}} - L_S^i,P_S^i \le \frac{{{\varepsilon ^2} + P_S^{ - i}}}{{g_S^i{g_J}}}\\ \left( {\frac{{g_S^i}}{{P_J^{{\rm{Max}}}{g_J} + P_S^{ - i} + \varepsilon }} - L_S^i} \right)P_S^i,P_S^i \ge \frac{{{L_J}{{\left( {P_J^{{\rm{Max}}}{g_J} + P_S^{ - i} + \varepsilon } \right)}^2}}}{{\left( {g_S^i{g_J}} \right)}}\\ \sqrt {\frac{{g_S^iP_S^i{L_J}}}{{{g_J}}}} - L_S^iP_S^i,{\rm{ 其他 }} \end{array} \right. \end{array} $

(16)

假设函数$H\left( {P_s^i} \right) = \sqrt {g_s^iP_s^i{L_J}/{g_J}} - L_s^iP_s^i$, 其一阶导数${\rm{d}}H/{\rm{d}}P_s^i = 0.5\sqrt {g_S^i{L_J}/P_S^i{g_J}} - L_S^i$, 二阶导数d_H²/d(P_sⁱ)²≤0, 因此H(P_Sⁱ)为凹函数, 则有$\tilde P_s^i = \max H = L_S^ig_S^i/\left( {4{g_J}L_S^i} \right)$。由式(16)可知, 节点i的P_S^SE存在以下情况:

1) L_Sⁱ>g_Sⁱ/(ε+P_S^-i):U_S(P_Sⁱ, P_S^-i, P_J)关于P_Sⁱ递减, 此时P_S^SE=0。

2) $g_s^i/\left( {\varepsilon + P_s^{ - i} + P_J^{{\rm{Max}}}} \right) < L_s^i < g_s^i/\left( {\varepsilon + P_s^{ - i}} \right)$:如果$P_s^i \le {L_J}\left( {{\varepsilon ^2} + P_s^{ - i}} \right)/\left( {g_s^i{g_J}} \right), {U_s}\left( {P_s^i, P_s^{ - i}, {P_J}} \right)$关于P_Sⁱ不减, 当$P_S^i \ge {L_J}{\left( {P_J^{{\rm{Max}}}{g_J} + P_s^{ - i} + \varepsilon } \right)^2}/\left( {g_S^i{g_J}} \right)$时, ${U_S}\left( {P_s^i, P_s^{ - i}, {P_J}} \right)$递减, 此时$P_s^{{\rm{SE}}} = \hat P_s^i$。

3) $L_s^i < g_s^i/\left( {\varepsilon + P_s^{ - i} + P_J^{{\rm{Max}}}} \right):{U_s}\left( {P_s^i, P_s^{ - i}, {P_J}} \right)$关于P_Sⁱ递增, 此时P_S^SE=P_S^Max, 则求得P_S^SE为:

$ P_S^{{\rm{SE}}} = \left\{ {\begin{array}{*{20}{l}} {0,L_S^i > \frac{{g_S^i}}{{\varepsilon + P_S^{ - i}}}}\\ {\frac{{g_S^i{L_J}}}{{4{g_J}L{{_S^i}^2}}}\frac{{g_S^i}}{{\varepsilon + P_S^{ - i} + P_J^{{\rm{Max}}}}} < L_S^i < \frac{{g_S^i}}{{\varepsilon + P_J^{{\rm{Max}}}}}}\\ {P_S^{{\rm{Max}}},L_S^i < \frac{{g_S^i}}{{\varepsilon + P_S^{ - i} + P_J^{{\rm{Max}}}}}} \end{array}} \right. $

(17)

综上所述, 本文提出的MDJC-AJ算法实现过程描述如下:

输入   训练数据$D = \left\{ {\left( {{s_i}, {b_i}} \right)\mid {s_i} \in S, {b_i} \in A} \right\}$, 经验池E

输出   最优策略的估计π_θ^*, 接收信号的信干噪比γ

1) 初始化。C_secⁱ(0)=0, 最大迭代次数N_it, 网络参数θ←0, w←0, 学习率α与β, 折扣因子λ, 熵正则化系数η, 干扰容忍阈值P_Jth1^sec与P_Jth2^sec。

2) 迭代更新。对每个智能体(节点/簇头), 每幕执行以下操作:

(1) 采样:根据状态s和动作b得到采样值C_secⁱ和下一个状态s′, 数据存储E←{s, b, C_secⁱ, s′}。

(2) 执行:利用π_θ(·|s′)得到动作b′。

(3) 通信安全容量:C_secⁱ(s)←C_secⁱ+λC_secⁱ(s′)。

(4) 策略更新:基于式(9), 更新策略网络参数w。

(5) 价值更新:基于式(10), 更新策略网络参数θ。

(6) 更新状态与动作:s←s′, b←b′。

(7) 信道选用策略:判断前一时刻被选信道在当前时刻的干扰等级, 当等级为3时, 最佳传输功率为0, 奖励函数C_secⁱ(s)=0时, 则转至(1)采样操作; 当等级为2时, 建立功率域博弈模型, 由式(17)得到最佳传输功率; 当等级为1时, 则保持使用当前信道。

3) 直至达到最大迭代次数N_it, 结束。

2.3 算法复杂度分析

参考文献[12], 本文对MDJC-AJ算法的复杂度进行分析, 结果如表 2所示。

本文算法的运算复杂度分析描述如下:

1) 对于单个节点i或簇头, 获得观测状态和得到采样值C_secⁱ的复杂度为O(C_i), C₁为与采样过程相关的常数, 所有的节点运算复杂度为O(N_SC₁), 该部分对应算法迭代更新中的步骤1。

2) 对于单个节点, 根据策略π_θ(·|s′), 在每个状态下执行相应动作得到奖励值的复杂度为O(C₂), C₂为与策略类型相关的常数, 所有节点的运算复杂度为O(N_SC₂), 该部分对应算法迭代更新中的步骤2、步骤3。

3) 对于单个节点, 基于式(9)、式(10), 更新参数w、θ以及状态s、动作b, 运算复杂度为O(C₃), C₃为与每幕的时间步长或收敛迭代次数相关的常数, 所有节点的运算复杂度为O(N_SC₃), 该部分对应算法迭代更新中的步骤4~步骤6。

4) 对于单个节点, 根据阈值进行等级划分, 运算复杂度为O(C₄), C₄为与阈值个数相关的常数, 所有节点的运算复杂度为O(N_SC₄)。

5) 干扰机最佳干扰功率运算复杂度为O(C₅), C₅为与式(15)相关的常数。

6) 对单个节点, 根据式(17)计算节点最佳传输功率运算复杂度为O(C₆), C₆为常数, 所有节点的运算复杂度为O(N_SC₆)。

通过以上分析, 可得到MDJC-AJ算法的总运算复杂度为:

$ \begin{array}{*{20}{l}} {{C_{{\rm{ sum }}}} = {N_{it}}(O({N_S}{C_1}) + O({N_S}{C_2}) + O({N_S}{C_3}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} O({N_S}{C_4}) + O({C_5}) + O({C_6}))} \end{array} $

(18)

2.4 基于簇头协助的信道选择算法

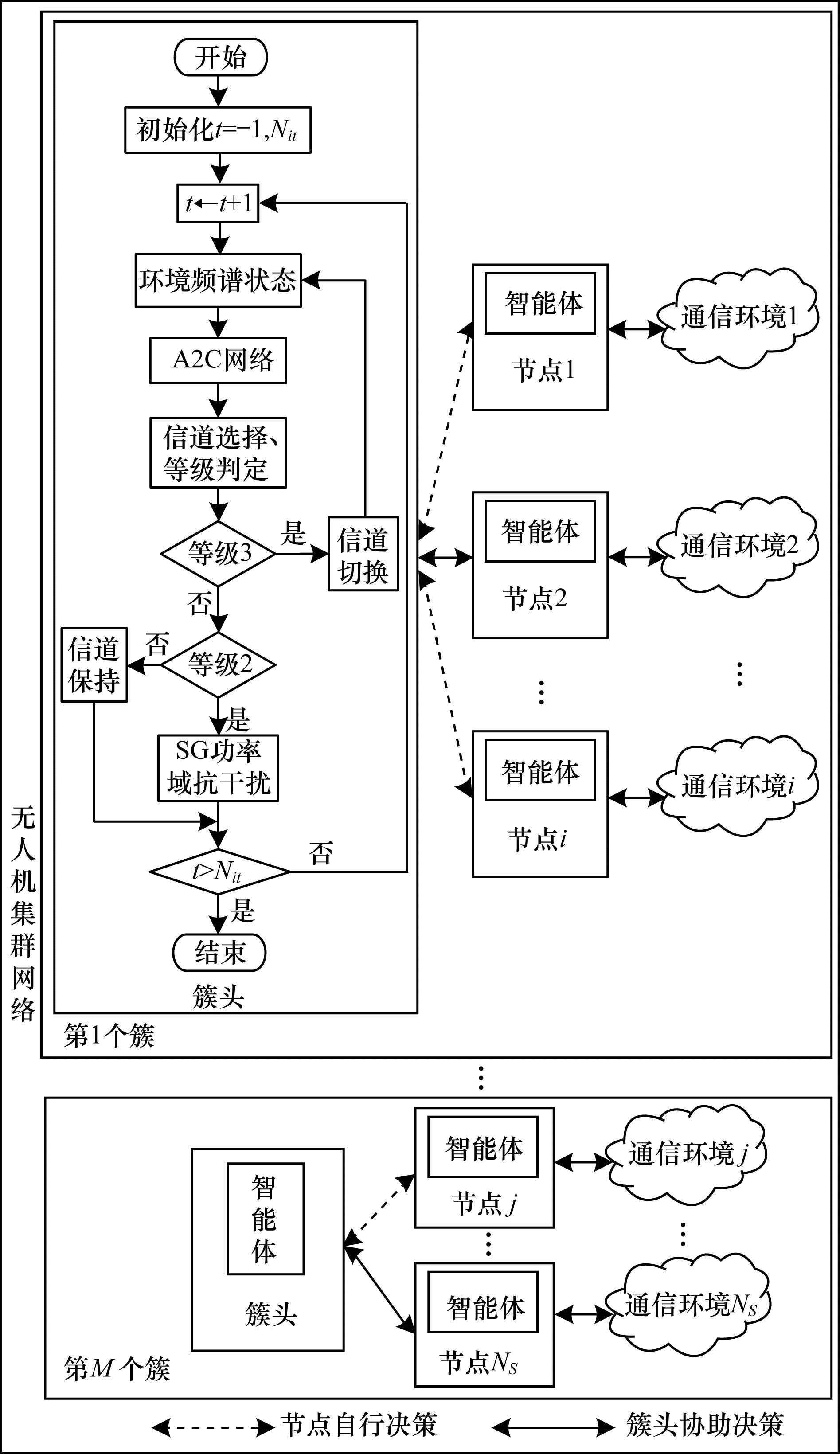
由于实际环境态势的多变性以及信息的局部性, 存在单个节点局部频谱感知能力有限的问题, 为此引入簇头协助从节点决策方法。基于簇头协助的无人机集群网络抗干扰示意图如图 2所示。

簇头协助从节点决策方法可描述为:各节点进行局部环境感知与信道决策时, 若某节点所得结果无法达到期望值, 则向簇头发出Help信息, 簇头收到求助信息后, 则向其传输无干扰信道数据信息, 使其能够进行可靠通信。需要说明的是, 所有节点和簇头均采用MDJC-AJ算法进行抗干扰。为了不失一般性, 图 2中仅详细说明第一个簇头内部抗干扰算法的实现流程。

3 实验仿真与分析

为验证本文所提算法的有效性, 实验选用卷积神经网络来拟合值函数和策略函数。仿真环境为Intel^®Core^TM i7-4790 CPU@3.60 GHz四核八线程处理器, 采用Pytorch1.2.0深度学习框架与Matlab2018a仿真平台。

仿真条件设置为:每幕训练时长T=5 000, 每个时间步长Δt=0.1 s, 每100幕为一个训练周期, 总共设有10个仿真周期, 经验池容量大小为E=10 000。设定信道个数K=32, 并将状态空间重塑为6×6的排列作为网络输入。为确保Critic有足够的时间计算奖励值, Critic网络学习率β=0.02, Actor网络学习率α=0.005, 惩罚系数η=0.3, 干扰功率阈值P_Jth1^sec=0.5、P_Jth2^sec=6。

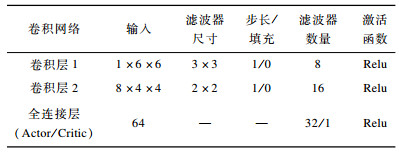
Actor网络与Critic网络基本一致, 不同的是最后的全连接层^[20]。Actor网络输出维度为32×1, 对应32个待选信道, Critic的输出维度为1, 用于计算Actor所获奖励。网络结构参数设置如表 3所示。

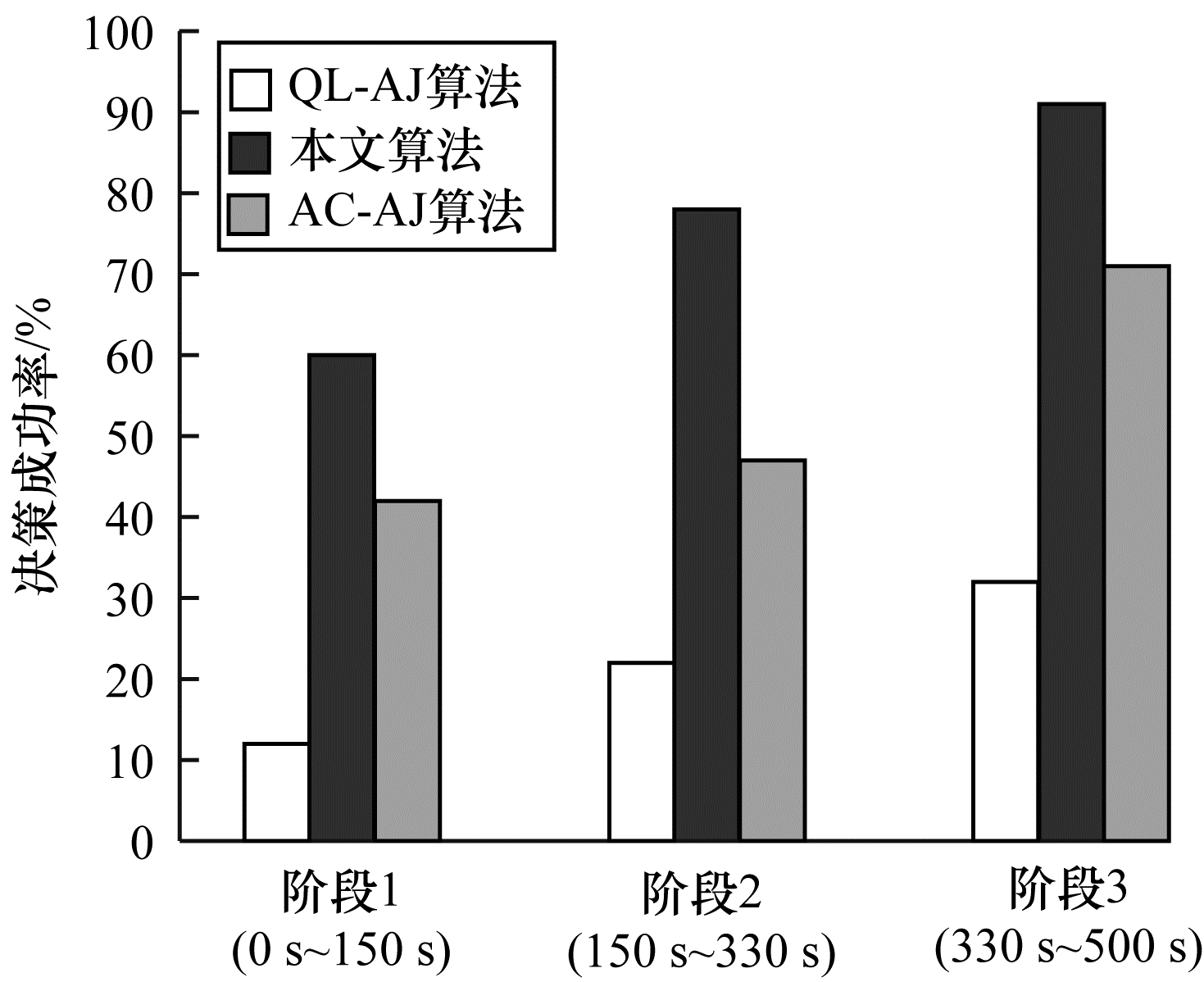
仿真1   为验证本文所提算法的信道选择性能, 考虑干扰机采用智能性干扰, 即不同时间段干扰机干扰的信道和功率均不同, 为便于分析将环境状态的时变点分别设在t_change=1 500和t_change=3 300, 网络中节点个数为4, 编队及所选簇头已最优。实验对文献[4]Q学习抗干扰(QL-AJ)算法、文献[8]演员-评论家抗干扰(AC-AJ)算法与本文算法的信道干扰情况决策成功率进行比较, 结果如图 3所示。从图 3可以看出, 在各个阶段内, 相比QL-AJ算法与AC-AJ算法, 本文所提MDJC-AJ算法的信道干扰情况决策成功率更高。

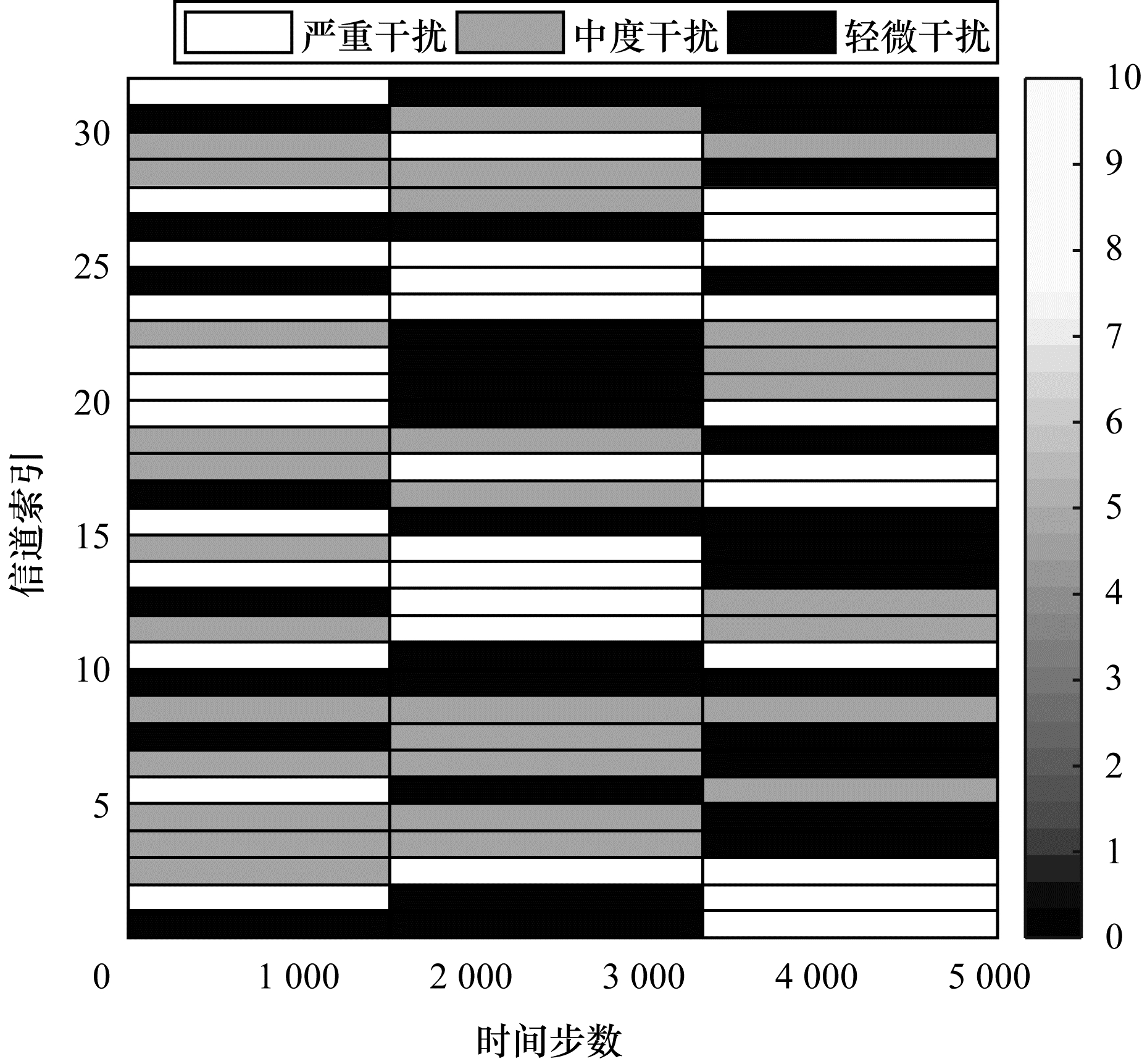
为进一步说明MDJC-AJ算法在智能性干扰情况下信道决策有效性, 由仿真所得信道干扰情况判决结果, 如图 4所示。从图 4可以看出, MDJC-AJ算法在决策出可用信道索引情况下, 对信道干扰功率情况进行判决, 可为功率域抗干扰提供依据。

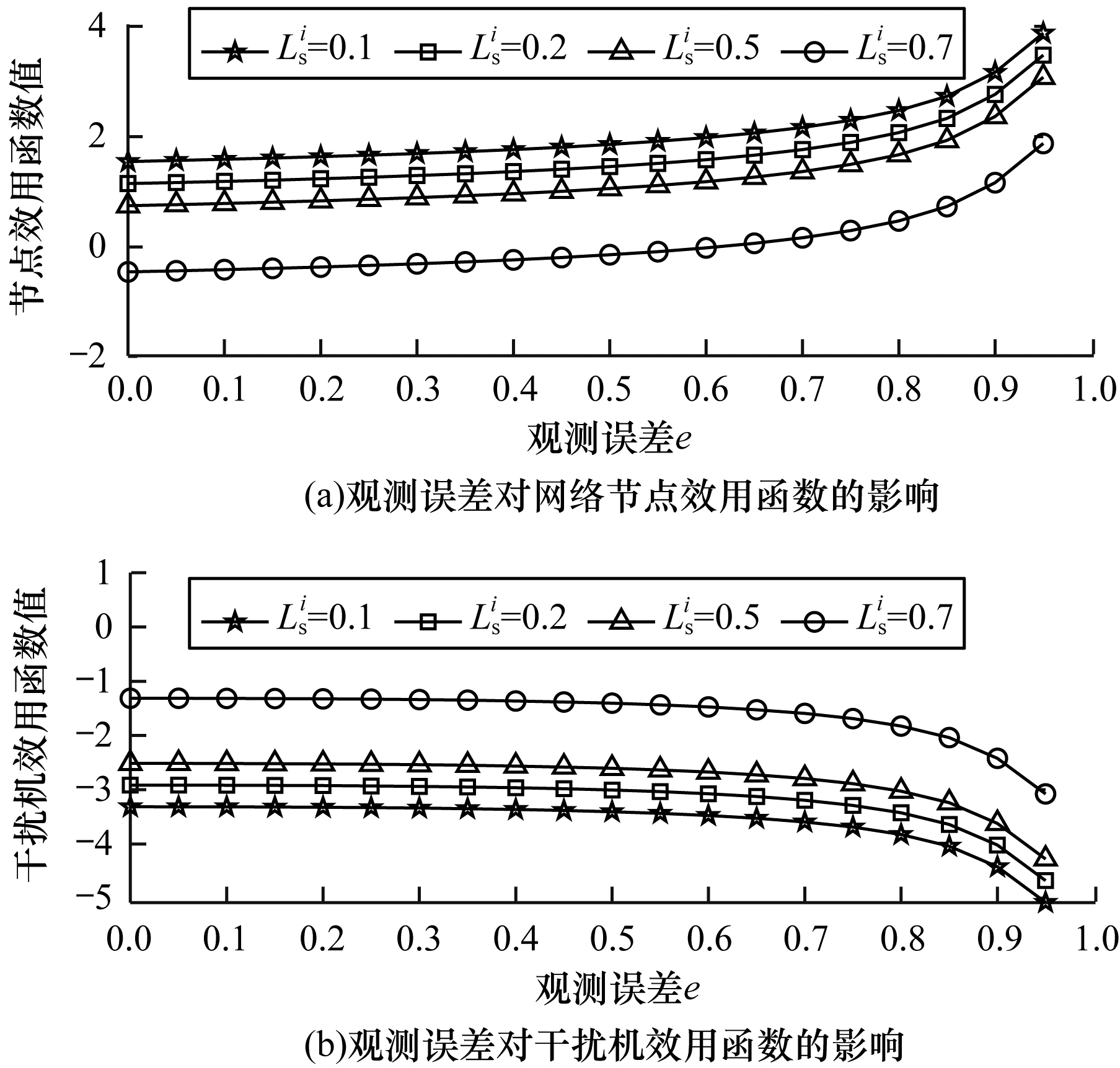
仿真2   考虑干扰机观测误差, 实验对干扰机偏离SE对节点效用函数及其自身效用函数的影响进行研究, 以检验网络的抗干扰性能。仿真参数设置为:通信信道增益g_Sⁱ=0.7、g_S^-i=0.2, 干扰机损耗系数L_J=0.4, 节点i传输功率与干扰机干扰功率分别为P_Sⁱ=12、P_J=10。为实现方便, 将簇内邻节点对节点i的互干扰功率均设为常数P_S^-i=2, 噪声功率ε=0.5, 节点损耗系数为L_Sⁱ=[0.1, 0.2, 0.3, 0.7]。干扰机观测误差e对节点效用函数之和${U_s} = \sum\limits_i^{{N_S}} {U_s^i} $与干扰机效用函数U_J的影响如图 5所示。

从图 5可以看出, 随着干扰机观测误差e的增加, 节点效用函数之和呈现递增趋势, 然而干扰机的效用函数呈现递减趋势。这是因为随着观测误差的增加, 使得干扰机最佳传输功率偏离SE, 导致其效用函数减小, 干扰机观测误差等效于削弱了干扰机干扰的强度, 而这将有利于提高节点效用函数, 使其通信性能提升。

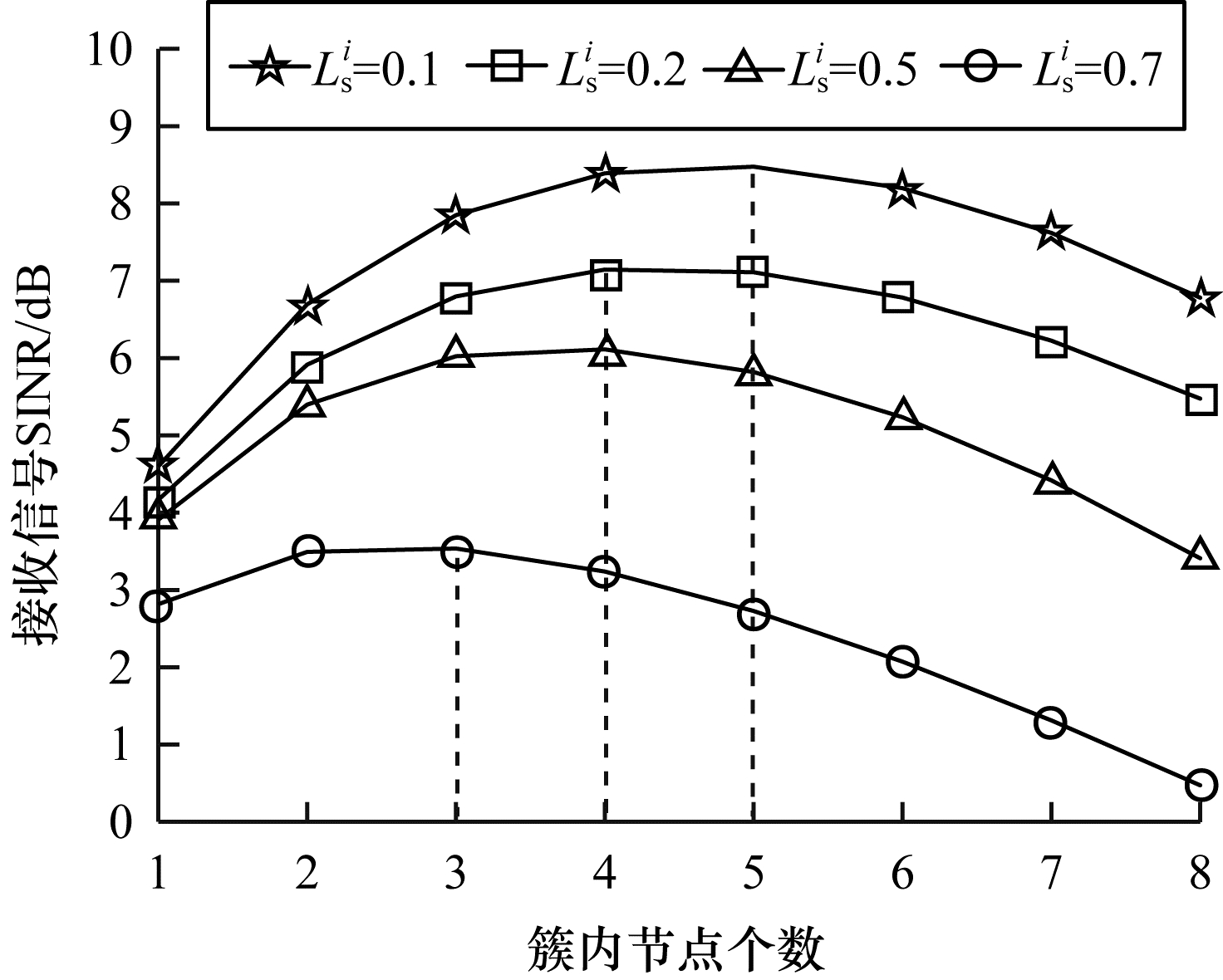
簇内节点个数对接收信号的SINR的影响如图 6所示。

从图 6可以看出, 随着节点数的增加, 接收信号的SINR呈现先增大后减小的趋势。这是由于随着簇内节点数的增加, 节点之间的互干扰不断增加, 使得单个节点接收信号的SINR降低, 进而导致簇内各节点接收信号的SINR降低。此外, 在不同的节点损耗系数L_Sⁱ=[0.1, 0.2, 0.3, 0.7]下, 簇内节点数存在一个最佳个数, 分别对应最佳簇内节点的个数为N_C=[5, 4, 4, 3], 在一定程度上可为无人机集群网络簇的划分提供有益参考。

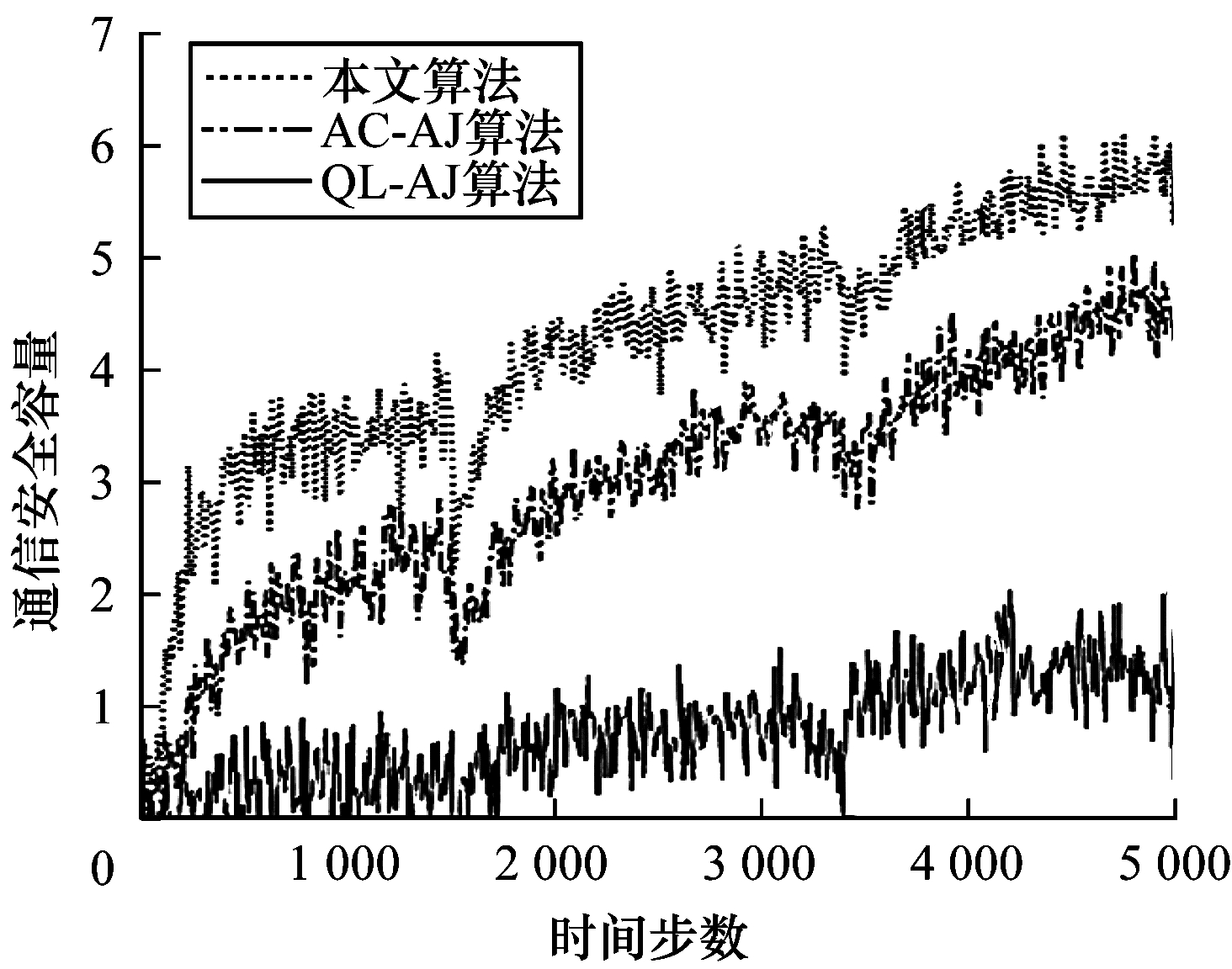
仿真3   实验比较了QL-AJ算法、AC-AJ算法与本文算法的抗智能干扰性能, 如图 7所示。从图 7可以看出, 在3种不同算法下, 网络通信安全容量均随着训练时间的增加而不断提高, 且与QL-AJ算法、AC-AJ算法相比, 本文算法的网络通信安全容量更高。值得注意的是, 在3个阶段的突变点, 上述3种算法得到的通信安全容量均骤减, 之后恢复, 然而本文算法较其他2种算法恢复的更快, 其原因是:由于状态空间和动作空间较大, QL-AJ算法遍历Q表所有状态的计算量庞大, 算法收敛较慢; 同时, AC算法利用卷积神经网络强大的计算能力, 相比QL算法提高了近4倍的计算速度; 另外, 相比于AC-AJ算法, 本文算法能够降低学习过程的方差, 算法稳定性好、收敛更快, 且通过联合功率域抗干扰减少信道切换的时间, 同时提高了接收信号SINR, 从而得到的通信安全容量更高。

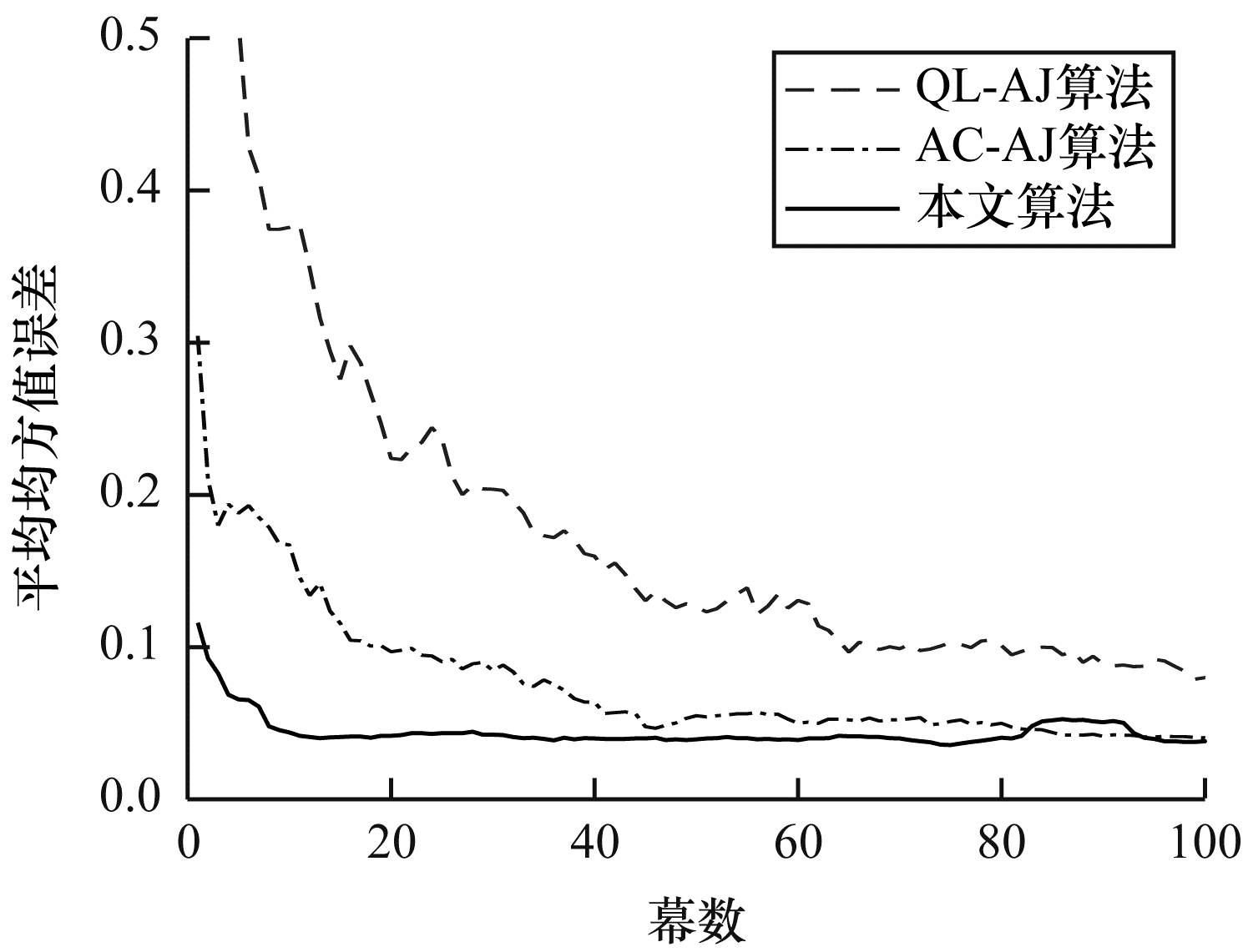
为进一步说明本文算法的稳健性, 定义单个状态s的均方值误差表示为近似值函数V_θ(s)与真实C_secⁱ(s)差的平方, 并记作VE :

$ \overline {{\rm{VE}}} = \sqrt {\frac{1}{{|S|}}\sum\limits_{s \in S} {{{\left[ {C_{{\rm{sec}}}^i(s) - {V_\theta }(s)} \right]}^2}} } $

(19)

其中, | S |为系统状态个数。

为验证所提方法算法收敛性能, 实验对比了QL-AJ算法、AC-AJ算法与本文算法的收敛情况。10个仿真周期的平均均方值误差如图 8所示。从图 8可以看出, 本文算法在经过10幕左右后已经收敛, 比其他2种算法的收敛性能好, 且得到的平均均方值误差更小。

4 结束语

针对无人机集群网络对抗智能性干扰能力较弱的问题, 本文提出一种MDJC-AJ算法。该算法基于A2C频域算法, 利用感知到的频谱状态信息进行信道选择, 以提高算法的收敛速度与信道决策成功率, 并在此基础上, 根据得到的功率干扰等级, 利用功率域进行抗干扰, 以减少信道切换时间、提高接收信号SINR。通过仿真对比QL-AJ算法与AC-AJ算法, 说明本文所提MDJC-AJ算法的整体抗干扰性能较好。同时, 本文采用簇头协助的方法进一步改善网络的抗干扰性能。后续将考虑实际物理场景中存在不完全观测信息的情况, 开展基于贝叶斯博弈理论的抗干扰方法研究, 以满足实际工程需要。