2. 中国科学院大学 电子电气与通信工程学院, 北京 100049;
3. 上海科技大学 信息科学与技术学院, 上海 201210;
4. 中国科学院上海微系统与信息技术研究所, 上海 200050
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Information Science and Technology, ShanghaiTech University, Shanghai 201210, China;
4. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China
随着信息社会的不断发展, 人们对定位服务的需求日益增多, 对室内环境而言, 由于信号的严重衰减和多径效应[1-2], 通用的室外定位设施并不能在建筑物内有效地进行工作, 因此人们需要更精密准确的定位方法。无线保真(Wireless Fidelity, WiFi)[3]作为基础定位设施成为研究人员首先考虑的方法。另外的一些技术, 如无线射频识别(Radio Frequency Identification, RFID)[4]、超声波、激光等, 也可以实现室内定位, 但是这些技术在真实环境中的实用性较低, 同时存在额外搭建网络设施导致的安装和工作成本增加的问题。
对WiFi定位算法而言[5], 由于WiFi的接收信号强度(Received Signal Strength, RSS)获取比较简单, 不受信号带宽的影响, 因此RSS是广泛应用于WiFi定位中的信号特征。WiFi定位最普遍应用的算法是指纹定位算法[6], 目前已有大量高准确率的改进算法被提出, 经典算法有贝叶斯算法[7-9]、EZ算法[10]等, 文献[11]提出一种新的高斯过程回归模型, 以估计室内环境的非均匀RSS分布, 但是误差在2 m以内占比仅60%, 1 m以内占比仅20%。
除经典算法外, 运用机器学习进行匹配的算法也被大量运用在WiFi室内定位领域。文献[12]引入一种相似度度量信号趋势指数, 使得定位精度平均达到2 m~3.5 m, 但是误差在2 m以内的占比仍不超过60%。文献[13]对离线指纹进行稀疏表示, 但是结果与采样点自身RSS变动规律严重冲突, 同时波动性太大, 标准差达到1.91 m。一般而言, 定位算法的采样点间距(网格)仅为1 m~2 m, 因此上述算法50%以上数据将被误定位成相邻网格, 严重影响定位精度。实际上, 无论是传统算法还是运用机器学习的算法都存在在低于2 m的误差范围内定位累计准确率过低的问题。特别是当相邻网格指代完全不同的信息时, 如在室内环境中智能手机使用者是生活区的某家餐厅内还是门外的走廊, 此时定位问题转化为了二分类问题, 在低于2 m的误差范围内过低的准确率会造成客观事实的严重错误。目前相邻网格问题的研究较少, 文献[14]利用Adaboost算法反复迭代和合并弱学习者的结果最终将定位数据分为室内和室外, 属于二分类问题, 并且没有研究相邻网格。
本文将室内场景下的相邻网格定位问题, 转化为对无线访问接入点(Access Point, AP)收集到的高维RSS数据进行0、1判决的问题, 为使判决具有有效性和稳定性, 提出一种去异常值的线性判别低维组合算法, 根据信号强度数据的自身特征对数据进行处理, 并运用线性判别低维组合算法对数据进行约束, 以满足WiFi室内定位的高精度要求。
1 系统模型和问题描述WiFi室内定位算法通常采用基于RSS的指纹定位算法, 指纹定位算法在离线训练阶段将室内区域划分为网格(间距1 m~2 m), 使用接收设备对网格采样点逐个进行采样, 每个网格对应一个独特的指纹, 这个指纹可以是单维或多维的, 是接收信息或信号的一个特征或多个特征, 通常可记录该点位置、所获取的RSS及AP地址等, 对指纹数据进行处理(滤波、均值等), 在大量的已知位置上建立一个细粒度的指纹数据库。在线定位阶段用户持移动设备在定位区域移动, 实时获取当前RSS及AP地址, 将该信息上传到服务器进行匹配。其中, 待定位设备的信号强度d与固定信号发射源的距离q符合如下传播模型:
| $ d = \frac{{{{10}^{\left( {\left| {{r_{{\rm{rss}}}}} \right| - E} \right)}}}}{{{{10}^q}}} $ | (1) |
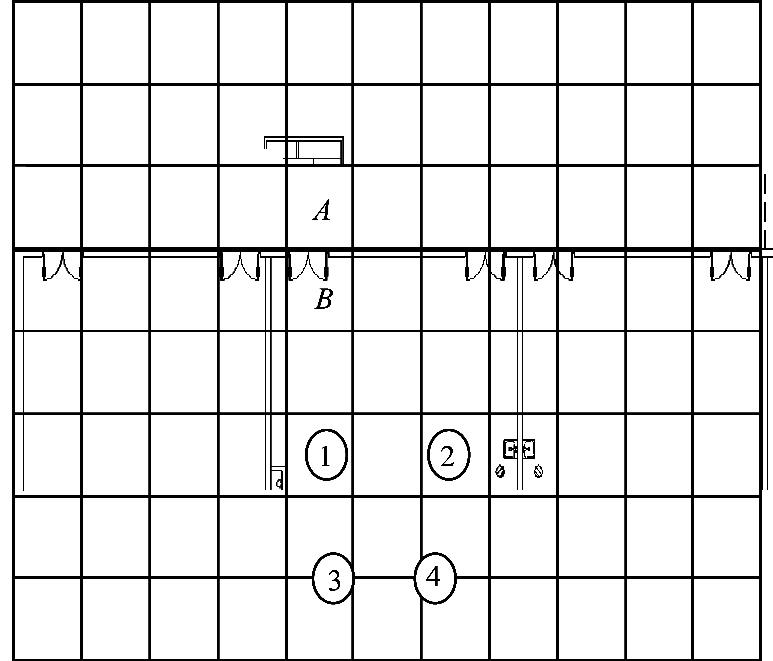
其中, E为发射端和接收端相隔1 m时的信号强度, q为环境衰减因子。本文选取的室内场景如图 1所示, 图 1中环境区域被划为不同网格(a m×b m), 虚线为网格边界, 总共有k个AP(k≥4), 其中AP用圆形表示, 特别地, 有4个AP分别为AP1、AP2、AP3、AP4, 用1、2、3、4标注。同一时刻k个AP对应收集的k维RSS数据为m=[RSS1, RSS2, …, RSSk]=M, 这里M为m组成的数据集合, M分为由离线阶段收集的数据m1组成的集合M1(训练集和验证集集合)和在线训练阶段收集的数据m2组成的集合M2(测试集)。
|
Download:
|
| 图 1 室内场景 Fig. 1 Indoor scene | |
本文的目的是通过对离线阶段收集的数据m1和对应的标签进行学习得到映射f, 从而判断在线训练阶段收集的数据m2输出的标签所对应的网格, 假设输出的标签为集合L={0, 1, …, T}, 分别对应T个网格, 室内定位问题即变成多分类问题, 数学形式如下:
| $ f:{M_2} \to L $ | (2) |
由于目前存在在低于2 m的误差范围内定位累计准确率过低导致误判为相邻网格的问题, 因此选择一对相邻网格作为研究对象, 特别地, 图 1中A和B两点分别代表门内网格和门外网格, 对应的标签为0或1这2个值, 集合为G={0, 1}, 离线学习得到模型g, 多分类问题转变为二分类问题, 如现实场景中具有较高实际价值的门内门外状态, 数学形式转变为:
| $ g:{M_2} \to G $ | (3) |
对于WiFi室内定位算法, 人们采用度量迁移学习(Metric Transfer Learning, MTL)、主成分分析(Principal Component Analysis, PCA)、随机森林(Random Forest, RF)算法、稀疏表达(Sparse Presentation, SP)等算法得到估算位置[15-17], 然而这些算法都是从整体区域的大尺度分类角度进行匹配, 最终的分类结果为适用于误差可允许范围在2 m以上的场景, 并不适合处理相邻网格的数据。因此, 本文引入线性判别分析(Linear Discriminant Analysis, LDA)算法[18], 首先处理异常值, 并且对LDA算法在低维情况下进行排列组合, 通过概率求和对在线训练数据进行新的约束, 最终确定智能手机使用者具体的二分类状态(如门内或门外)。
LDA算法是将高维的模式(多个AP样本, 不同AP对应不同维度)投影到最佳鉴别矢量空间, 以达到抽取分类信息和压缩特征空间维数的效果, 使投影后模式样本的类间散布矩阵最大, 同时类内散布矩阵最小, 保证投影后在新的空间中有最小的类内距离和最大的类间距离, 即相邻网格的高维数据在该空间中有最佳的可分离性。区分方法为:首先获取每类高维数据的均值(中心点)ui, 其中, w是投影方向, n为投影值, n=wTm, 投影值n被划分为2个集合。ti是所有被判定为i(i为0或1)的n的集合, 对应地, 集合si是判定为i的所有m的集合, Ni是所有被判定为i且属于集合M1点的个数。可以求得高维数据中心点ui为:
| $ {u_i} = \frac{1}{{{N_i}}}\sum\limits_{m \in {s_i}} m $ | (4) |
由m通过投影w后的样本点均值为vi:
| $ {v_i} = \frac{1}{{{N_i}}}\sum\limits_{m \in {s_i}} {{\mathit{\boldsymbol{w}}^{\rm{T}}}} m = {\mathit{\boldsymbol{w}}^{\rm{T}}}{u_i} $ | (5) |
投影后的均值即为样本中心点的投影, 则类间距离为J(w), 可表示为:
| $ J\left( \mathit{\boldsymbol{w}} \right) = \left| {{v_1} - {v_2}} \right| = \left| {{\mathit{\boldsymbol{w}}^{\rm{T}}}\left( {{u_1} - {u_2}} \right)} \right| $ | (6) |
类内距离ri2可表示为:
| $ r_i^2 = \sum\limits_{n \in {t_i}} {{{\left( {n - {v_i}} \right)}^2}} $ | (7) |
则最大化目标函数为:
| $ G\left( \mathit{\boldsymbol{w}} \right) = \frac{{{{\left| {{v_1} - {v_2}} \right|}^2}}}{{r_1^2 - r_2^2}} $ | (8) |
最终得到映射关系, 并根据映射关系w得到预测值:
| $ \mathit{\boldsymbol{w}} = K_\mathit{\boldsymbol{w}}^{ - 1}\left( {{u_1} - {u_2}} \right) $ | (9) |
其中,
在WiFi室内定位场景中, 本文选择LDA算法的原因是只要AP不是紧邻被测相邻网格, 就可以得到室内相邻网格(如门内门外)数据在各自网格内近似方差相等, 区分相邻网格主要与均值有关, 以证明以门内门外网格为例, 如果AP紧邻被测相邻网格, 根据式(1), 相邻网格信号强度差异巨大, 此时定位准确率本身就很高, 不是本文以及所有WiFi室内定位相关论文的讨论范围, 本文讨论的是普遍存在的一般定位研究中出现的在低于2 m的误差范围内定位累计准确率过低的问题。因此, 从理论上确立一个边界, 此边界可广泛适用于室内WiFi定位场景。WiFi信号传播示意图如图 2所示。
|
Download:
|
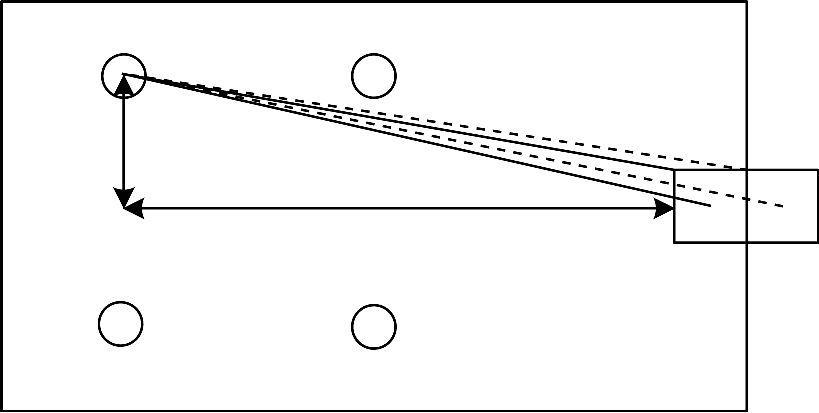
| 图 2 WiFi信号传播示意图 Fig. 2 Schematic diagram of WiFi signal propagation | |
在图 2中任意选择一个AP, AP用圆形表示, 门内门外的相邻网格分别用2个网格表示, 2条实线分别代表WiFi信号传播到门内的中心点和边缘点的2条视线传输的路径, 路径的距离分别用d1、c1表示, 2条虚线分别代表传播到门外的中心点和边缘点的2条视线传输的路径, 路径的距离分别用d2、c2, 横向双箭头所示距离为x, 纵向双箭头所示距离为y, 门内的中心点和边缘点的信号强度值为rrss1、rrss2, 则根据信号强度与距离式(1), 有:
| $ \frac{{{d_1}}}{{{c_1}}} = {10^{\left| {\Delta {r_{{\rm{rss}}1}}} \right|}} $ | (10) |
| $ \frac{{{d_2}}}{{{c_2}}} = {10^{\left| {\Delta {r_{{\rm{rss}}2}}} \right|}} $ | (11) |
从而可以得到:
| $ \Delta {r_{{\rm{rss}}1}} - \Delta {r_{{\rm{rss}}2}} = \lg \left( {\frac{{{d_1}{c_2}}}{{{d_2}{c_1}}}} \right) $ | (12) |
其中, Δrss1、Δrrss2分别是图 2所示门内、门外点在各自网格的角与中心的信号强度差值, 根据大小关系可知RSS同号。网格为a、b的格子形, 通过对下面等式做变换:
| $ \frac{{{d_1}{c_2}}}{{{d_2}{c_1}}} = \frac{{\left( {{{\left( {x + \frac{a}{2}} \right)}^2} + {y^2}} \right)\left( {{{\left( {x + a} \right)}^2} + {{\left( {y - \frac{b}{2}} \right)}^2}} \right)}}{{\left( {{x^2} + {{\left( {y - b\frac{b}{2}} \right)}^2}} \right)\left( {{{\left( {x + \frac{{3a}}{2}} \right)}^2} + {y^2}} \right)}} $ | (13) |
记
| $ \begin{array}{l} \frac{{{d_1}{c_2}}}{{{d_2}{c_1}}} = \\ \frac{Q}{{Q + \left( {2ax + 2{a^2}} \right)\left( {\frac{{ - {a^2}}}{4} + \frac{{ - {b^2}}}{4} - ax - by} \right) + {a^2}{{\left( {x + \frac{a}{2}} \right)}^2}}} = \\ \frac{Q}{{Q + {a^2}\left( {{y^2} - ax + by + \frac{{{b^2}}}{2} - \frac{{{a^2}}}{4}} \right) + ax\left( {\frac{{{b^2}}}{2} - ax - by - \frac{{{a^2}}}{2}} \right)}} \end{array} $ | (14) |
由于网格的边长a、b一般都在1 m到2 m之间(网格边长等于相邻网格的中心距离, 而低于2 m的误差范围内是相邻网格的中心距离, 即本文所研究的距离区分度), 距离比较小, 记:a2(y2-ax-by)+ax(-ax-by)为R, 式(14)可近似为:
| $ \begin{array}{l} \frac{{{d_1}{c_2}}}{{{d_2}{c_1}}} = \frac{Q}{{Q + {a^2}\left( {{y^2} - ax - by} \right) + ax\left( { - ax - by} \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\frac{Q}{{Q + R}} \end{array} $ | (15) |
任意AP需满足如下条件:
| $ {x^2} + {y^2} \in \left( {4a\max \left( {a,b} \right),\infty } \right) $ | (16) |
对式(15)中的R进行缩放, 可以得到:
| $ \begin{array}{l} - 2a\max \left( {a,b} \right)\left( {{x^2} + {y^2}} \right) \le \\ - a\max \left( {a,b} \right){\left( {x + y} \right)^2} \le - \left( {{a^2} + ax} \right)\left( {ax + by} \right) \le R\\ R \le {a^2}\left( {{y^2} - {x^2}} \right) \le {a^2}\left( {{x^2} + {y^2}} \right) \end{array} $ | (17) |
从而比较式(15)分子分母, 近似可得:
| $ \begin{array}{l} \frac{{{x^2} + {y^2}}}{{\left( {{x^2} + {y^2}} \right) + {a^2}}} \le \frac{{{d_1}{c_2}}}{{{d_2}{c_1}}} \approx \frac{{\left( {{x^2} + {y^2}} \right)\left( {{x^2} + {y^2}} \right)}}{{\left( {{x^2} + {y^2}} \right)\left( {{x^2} + {y^2}} \right) + R}} \le \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{x^2} + {y^2}}}{{\left( {{x^2} + {y^2}} \right) - 2\max \left( {a,b} \right)}} \end{array} $ | (18) |
不等式(18)两端边界均在式(16)的下确界取得, 因而对式(18)进行边界处理, 由式(12)得:
| $ \Delta {r_{{\rm{rss}}1}} - \Delta {r_{{\rm{rss}}2}} \in \left( {\lg \frac{4}{5},\lg 2} \right) = \left( { - 0.097,0.301} \right) $ | (19) |
上述推导过程证明了网格的角符合信号强度差值几乎相等的结论, 网格其他边界的点与上述推导过程类似, 网格内部的点到AP距离差值较小, 而信号强度值差值则更小, 由于任何在内网格的两点位置相对空间关系, 都可以找到对应向右(或者相邻方向)平移a的外网格的相对空间关系, 因此因空间位置改变的信号强度值在各自网格内方差几乎相同。相邻网格数据的方差主要分为空间位置σ1和自身能量波动σ2两部分, 而自身能量波动主要受发射点能量变化和到达时间变化决定, 因而对同一个AP发射点可认为在相邻网格自身能量波动σ2近似, 从而一维数据方差近似, k维数据方差由于独立性是一维数据方差的简单代数相加, 因此k维数据在各自网格内方差近似, 所以LDA算法用以突出类间距离对于处理中心距离低于2 m以内的相邻网格是合理的。
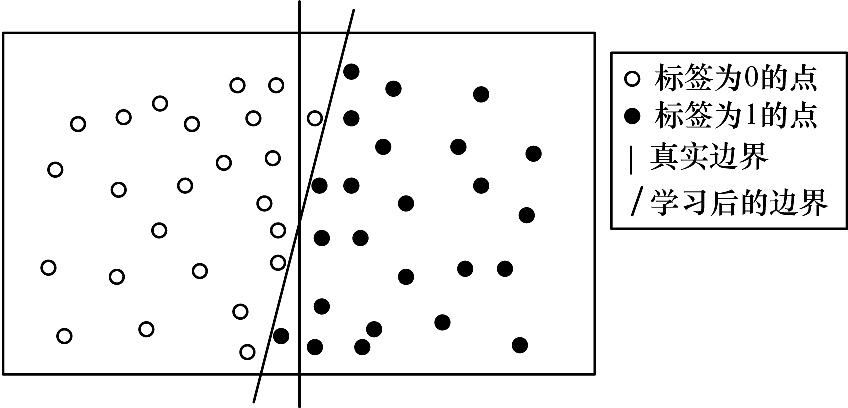
4 异常值处理方法对搜集的相邻网格的高维数据, 其数据部分交互重叠的特征如图 3所示(图 2描述的是3维)。在图 3中, 假设实际真正有效的分界线是中垂线, 但由于出现一些波动值(位于中垂线左边的黑点, 右边的白点), 若简单地以训练集位置划分, 则训练出的分界线是斜线, 显然失真, 必须设计一种异常值去除方法。异常值处理的原理是把数据集分为内群数据和离群数据, 其中离群数据则是不适合模型化的数据, 对模型构造有负面效果。在以m=[RSS1, RSS2, …, RSSk]的k维数据建立的坐标空间内, 由于每一维的RSS自身波动性较大而且处于相邻网格点, k维数据会出现混叠, 如式(7)所示会造成ri2失真, 进而影响式(8)的结果, 最终使w出现偏移。在图像拼接等领域, 人们通常采用Ransac算法[19]进行异常值去除, Ransac算法通过设置若干内点, 将离线训练的点代入内点模型, 如果残差不在预先设定的阈值内, 则被认为是异常值。
|
Download:
|
| 图 3 异常值对结果影响的示意图 Fig. 3 Schematic diagram of the effect of outliers on the results | |
如果运用Ransac算法, 则无法设定阈值。本文的处理方法是将离线训练的k维数据代入离线训练集自身, 寻找欧几里得距离最近的N0个点, 用欧几里得距离直接判断, 当检测任意的m0为k维数据异常点时, m′是异于m0的其他点, 欧几里得距离表达公式如下:
| $ {d_m} = {\left\| {{m_0} - {m^\prime }} \right\|_2} $ | (20) |
如果最近的N0个点中至少有一半以上的点与对应的网格一致, 则认为不是异常点; 否则视为异常点。
5 LDA低维组合算法采用LDA算法对k维数据进行0、1判决, 等价于0概率是否为0.5的判断, 实际上可以在数据的判断方面进行更严格的约束, 以提升判决准确率, 因而本文提出一种可以严约束的低维组合算法进行低维排列组合, 对所得的若干个概率值求和, 并设置门限。
算法描述分为训练验证和测试, 本文已经证明满足给定条件的任意AP均完全适用LDA算法。
训练验证阶段步骤如下:
1) 对k个AP产生的时序校准过的一维训练数据集分别进行归一化。
2) 对归一化后的数据进行异常值处理。
3) 对进行异常值处理后的数据运用LDA算法构建模型h。
4) 排列组合k个AP, 并分为k组, 每组依次去除一个AP(一维), 得到k-1维数据, 对k组k-1维数据运用LDA算法, 分别得到输出的预测值为0的概率P1, P2, …, Pk, 则对应预测值为1的概率分别为(1-P1), (1-P2), …, (1-Pk)。
5) 设置约束门限, 点m如果满足下式, 则m判决值取0:
| $ {P_1} + {P_2} + \cdots + {P_k} \ge k\lambda $ | (21) |
6) 对应地, 如果满足下式, 则m判决值取1:
| $ {P_1} + {P_2} + \cdots + {P_k} \le k\left( {1 - \lambda } \right) $ | (22) |
7) 如果概率和不在步骤4)和步骤5)范围, 则认为步骤2)的预测值是对的, 其中, λ∈(0.5, 1)。
测试阶段步骤如下:
1) 对k个AP产生的时序校准过的每一维在线训练数据分别进行归一化。
2) 用模型h预测k维归一化后的在线训练数据, 得到预测值(0或1)。
3) 重复训练验证阶段的步骤4)~步骤7)。
6 实验结果与分析 6.1 真实数据实验实验选用华为手机NEM-10作为接收设备, 其中手机内置有WiFi模块, 办公室内放置有4个AP, 通过HL-340 USB串行口分别与4台个人计算机相连。在测试前对AP内核写入程序并充分调试, 使AP在接收到手机反向的应答信号时, 将RSS信息、手机的MAC地址、收到应答信号的时刻通过串行口输出到个人计算机上, 并进行同时性校准。测试时个人计算机保存记录并整合4台个人计算机的信息。
实验所用的真实环境为办公室环境(见图 1), 其中办公室所在的门内网格和走廊所在的门外格点用A、B标注, 4个AP位置分别是AP1、AP2、AP3、AP4所在的位置, 选取的相邻格点是门内以门为边界线的内网格和门外对应的外网格(本文网格为1 m×1 m的正方形, 即相邻网格中心距离可以充分保证算法处理的数据低于2 m误差范围, 实现网格区分度最小时的准确率提升, 同时为使准确率提升更具有一般性, 门内门外没有门的阻隔, 这样相邻网格信号强度差异本身更小, 网格之间区分难度更大), 实验时实验人员携带手机在室内室外网格的时间相等, 实验人员每6 min轮换网格(这样可以保证训练数据的均衡性), 共分3个时间段进行3次不同真实办公室环境(如办公室内物体的摆放以及人员的变化)的实验。具体而言, 该办公室环境内外人员和物体(如人员的背包、笔记本等放置的位置)具有一定的流动性和进行社会活动的特征, 3次实验环境的人数在8人到13人之间波动, 同时办公室外的走廊上也会有行人经过。对办公室内部署的4个AP而言, 有2个AP部署在附近(约一个小网格尺度)较为空旷的地方, 其信号会被流动人员的活动(比如行走聚集等)随机干扰; 另有2个AP部署在两张有人持续使用的的办公桌上, 其信号不仅被随机干扰, 还会被办公设施具体使用者频繁干扰(如翻阅文件、变换坐姿等)。这样可以保证3次实验环境的不同, 对应地可以分别获取3种在真实变动环境(实际环境中存在人员和物体相对无变化的环境, 真实变动环境要求算法泛化能力更强)的不同数据集。第1种环境共收集2 383组的4维数据, 第2种环境总共收集535组的4维数据, 第3种环境总共收集957组的4维数据, 计算机总计收集到3 875组的4维数据。
6.2 结果分析根据实验设备得到的数据, 对数据处理后的去异常值的LDA低维组合算法与LDA算法、支持向量机(Support Vector Machine, SVM)算法进行比较研究[20], 其中文献[21]运用SVM算法通过基站确定全球移动通信系统(GSM)制式手机位置, 具有较好的鲁棒性, 并具备泛化能力强的特征。
对去异常值的LDA低维组合算法的λ分别取0.7、0.8、0.9, N0分别取50、75、100, 结果表明, 去异常值的LDA低维组合算法本身对于λ和N0这2个参数不敏感, 当λ比较大而N0不是太小时, 去异常值的LDA低维组合算法在各种环境下总的判断准确的数据个数波动始终在2个以内, 对测试集准确率影响忽略不计, 原因在于算法准确率提高, 对参数依赖性比较低。
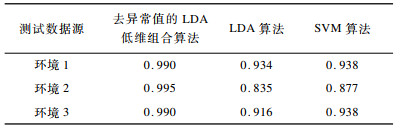
本文首先对每种相同环境划分为训练集、验证集和测试集3个部分。如环境1自身被随机分为3个部分, 即测试集也来自于环境1, 同理环境2、环境3自身内部也被随机地划分为3个部分, 分别得到各自在3种算法下的测试集准确率, 如表 1所示。
|
下载CSV 表 1 不同环境下3种算法测试集准确率比较 Table 1 Comparison of testing sets accuracy of three algorithms in the different environment |
从表 1可以看出, 去异常值的LDA低维组合算法在同一种环境下, 能准确地区分出多维数据位于相邻网格的哪一侧, 相对于LDA算法、SVM算法有比较明显的提升。
利用任一环境下的数据集作为训练集进行3种算法的训练和验证, 在实验中表示一次离线数据收集过程, 用其他环境下的实测数据集的任一实测数据作为测试集进行测试, 获得测试集的准确率, 如环境1作为训练验证集, 其他环境作为测试集, 用来验证算法的泛化能力, 以检验算法在一次离线采集基础上对不同环境下相邻网格的分辨能力。
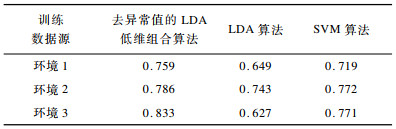
表 2为去异常值的LDA低维组合算法、LDA算法、SVM算法在办公室不同环境下对完整的训练集进行学习的准确率, 可以看出去异常值的LDA低维组合算法对比另外2种算法, 在每一种状态下准确率都有提高。这是由于去异常值的LDA低维组合算法根据相邻网格点RSS数据特征进行了合理的处理, 并且低维组合的思想通过概率和和门限的设置, 进行了对数据的约束。在上述方法的应用下, 在环境1中, LDA的准确率为65%, SVM的准确率为72%, 去异常值的LDA低维组合有至少4%的提升; 在环境2中, LDA的准确率为74%, SVM的准确率为77%, 去异常值的LDA低维组合为79%;在环境3中, LDA的准确率为63%, SVM的准确率为77%, 去异常值的LDA低维组合为83%, 具有显著提升。3种环境下的实验结果表明了本文算法的正确性和有效性。
|
下载CSV 表 2 不同环境下3种算法训练集准确率比较 Table 2 Comparison of training sets accuracy of three algorithms in different environments |
对于不同的环境, 3种算法的准确率具有比在相同环境下区分相邻网格有显著下降, 这符合信号强度受外界因素变化较大的现实情况, 表明室内Wifi定位的准确率在低于2 m的误差范围内过低的问题确实存在, 文献[6-8]的准确率与本文实际测试的LDA算法、SVM算法准确率结果是一致的, 这也表明本文算法是有效的。
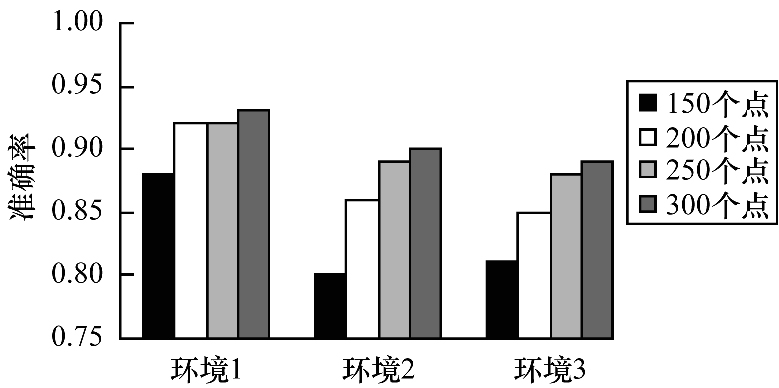
图 4是在不同办公室环境下, 训练集抽取不同数量的数据对去异常值的LDA降维组合算法的准确率, 从图中可以看出, 在相同的办公室状态下, 环境1要随机抽取250个数据, 训练达到测试集准确率的上限0.93, 在实际训练过程中抽取200个点时, 准确率虽然平均达到0.92, 但是随着抽取的随机状态不同而波动, 表明随机抽取200个点数据具有局限性而容易过拟合, 训练集至少需要250个点; 环境2要随机抽取300个数据, 训练达到准确率的上限0.90, 环境3要随机抽取300个数据, 训练达到准确率的上限0.89, 在实际训练过程中抽取250个点时, 环境2、环境3准确率虽然平均达到0.89、0.88, 但也会随着抽取的随机状态不同而波动, 表明随机抽取250个点数据具有局限性而容易过拟合, 至少需要300个点, 因而实施算法所需的训练集至少要有300个点。同时, 在实际训练过程中, 只要训练集抽取超过300个点, 无论选择何种环境, 去异常值的LDA低维组合算法的准确率不随抽取的随机状态而改变, 这表明该算法具有鲁棒性。
|
Download:
|
| 图 4 不同办公室环境下LDA降维组合算法的准确率 Fig. 4 Accuracy of LDA dimensionality reduction combined algorithm in different office environments | |
从表 1、表 2、图 4的结果可以看出, 去异常值的LDA低维组合算法可以有效提高本文所述二分类(如门内门外状态)的判决准确率, 具有正确性和鲁棒性。
7 结束语本文提出一种去异常值的线性判别低维组合算法。通过对室内WiFi定位的信号强度数据自身特征的研究, 完成LDA适用性和去异常值的理论分析, 并利用线性判别算法在低维情况下进行排列组合, 对所得的若干个概率值求和, 通过门限的设置对数据进行额外的约束。实验结果表明, 该算法能满足企业和用户对基于位置的定位服务的需求。本文方法主要用于小网格, 下一步将研究传统大尺度粗略分类与小尺度精确定位的联合算法, 以及WiFi定位与其他定位方法的联合判决来提高定位准确率。
| [1] |
JIANG Fang, DU Zhiqiang, GU Xiaopeng. Analysis of direction finding error caused for multipath effect[J]. Communication Confrontation, 2004(4): 30-32. (in Chinese) 姜芳, 杜志强, 谷晓鹏. 对多径效应引起测向误差的分析[J]. 通信对抗, 2004(4): 30-32. |
| [2] |
CHAO Whenxi, WU Tingfang, YANG Yuezhong, et al. Monte Carlo simulations of the optical buoy's shading effects[J]. High Technology Letters, 2003, 13(3): 80-84. (in Chinese) 曹文熙, 吴廷芳, 杨跃忠, 等. 光学浮标阴影效应的蒙特卡洛模拟[J]. 高技术通讯, 2003, 13(3): 80-84. DOI:10.3321/j.issn:1002-0470.2003.03.019 |
| [3] |
ATIA M M, NOURELDIN A, KORENBERG M J. Dynamic online calibrated radio maps for indoor positioning in wireless local area networks[J]. IEEE Transactions on Mobile Computing, 2013, 12(9): 1774-1787. DOI:10.1109/TMC.2012.143 |
| [4] |
QI Lilei, LIANG Zhixue, FENG Gaofeng. Design and implementation of an indoor location method based on UHF-RFID[J]. Computer and Digital Engineering, 2013, 41(4): 673-675. (in Chinese) 齐立磊, 梁智学, 冯高峰. 一种基于高频RFID的室内定位方法的设计与实现[J]. 计算机与数字工程, 2013, 41(4): 673-675. DOI:10.3969/j.issn.1672-9722.2013.04.051 |
| [5] |
DU Yuanfeng, YANG Dongkai, XIU Chundi. A novel method for constructing a WiFi positioning system with efficient manpower[J]. Sensors, 2015, 15(4): 8358-8381. DOI:10.3390/s150408358 |
| [6] |
NOGUEIRA R F, LOTUFO R D A, MACHADO R C. Fingerprint liveness detection using convolutional neural networks[J]. IEEE Transactions on Information Forensics and Security, 2017, 11(6): 1206-1213. DOI:10.1109/TIFS.2016.2520880 |
| [7] |
ANDREW M L, KOSTAS E B, ALGIS R, et al. Robotics-based location sensing using wireless Ethernet[J]. Computer Networking, 2002, 11(1/2): 227-238. |
| [8] |
TEEMU R, PETRI M, HENRY T, et al. A probabilistic approach to WLAN user location estimation[J]. International Journal of Wireless Information Networks, 2002, 9(3): 155-164. DOI:10.1023/A:1016003126882 |
| [9] |
GU Fufei, LUO Ying, CHEN Yijun, et al. Cognitive ISAR imaging technique of moving targets based on sparse processing[J]. Modern Radar, 2018, 40(11): 37-42. (in Chinese) 顾福飞, 罗迎, 陈怡君, 等. 基于稀疏处理的运动目标认知ISAR成像技术[J]. 现代雷达, 2018, 40(11): 37-42. |
| [10] |
KRISHNA C, ANAND P I, VENKATA N P. Indoor localization without the pain[J]. Computer Networking, 2010, 49(1): 173-184. |
| [11] |
ZOU H, JIN M, JIANG H, et al. WinIPS:WiFi-based non-intrusive indoor positioning system with online radio map construction and adaptation[J]. IEEE Transactions on Wireless Communications, 2017, 16(12): 8118-8130. DOI:10.1109/TWC.2017.2757472 |
| [12] |
ZOU Han, HUANG Baoqi, LU Xiaoxuan, et al. A robust indoor positioning system based on the procrustes analysis and weighted extreme learning machine[J]. IEEE Transactions on Wireless Communications, 2016, 15(2): 1252-1266. DOI:10.1109/TWC.2015.2487963 |
| [13] |
CHEN K Y, YUE M, SHEN Y, et al. SparseLoc:indoor localization using sparse representation[J]. IEEE Access, 2017, 5: 20171-20182. DOI:10.1109/ACCESS.2017.2727504 |
| [14] |
LOPEZ-DE-TERUEL P E, CANOVAS O, RUIZ A. Detecting indoor/outdoor places using WiFi signals and AdaBoost[J]. IEEE Sensors Journal, 2017, 17(5): 1443-1453. DOI:10.1109/JSEN.2016.2640358 |
| [15] |
SUN Tangle, LI Guohui. EEMD and RBF neural network prediction of sunspot monthly mean[J]. Computer Engineering and Applications, 2017, 53(24): 252-256. (in Chinese) 孙堂乐, 李国辉. EEMD与RBF神经网络的太阳黑子月均值预测[J]. 计算机工程与应用, 2017, 53(24): 252-256. DOI:10.3778/j.issn.1002-8331.1606-0395 |
| [16] |
BAO Hongyun, LI Qiudan, SONG Shuangyong, et al. Relevance feedback-based search of topic time series similarity in micro-blogging[J]. Computer Science, 2013, 40(4): 169-171. (in Chinese) 包红云, 李秋丹, 宋双永, 等. 基于相关反馈的微博相似主题时序查询[J]. 计算机科学, 2013, 40(4): 169-171. DOI:10.3969/j.issn.1002-137X.2013.04.037 |
| [17] |
DONG Yadong, LI Zhengyu, WANG Yang. Tree-structured data processing method based on model space[J]. Computer Engineering, 2017, 43(4): 194-199, 206. (in Chinese) 董亚东, 李正宇, 汪阳. 基于模型空间的树形数据处理方法[J]. 计算机工程, 2017, 43(4): 194-199, 206. DOI:10.3969/j.issn.1000-3428.2017.04.033 |
| [18] |
BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs.fisherfaces:recognition using class specific linear projection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(7): 711-720. DOI:10.1109/34.598228 |
| [19] |
FISCHlER M A, BOLLES R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. DOI:10.1145/358669.358692 |
| [20] |
HSU C W, LIN C J. A comparison of methods for multiclass support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415-425. DOI:10.1109/72.991427 |
| [21] |
WU Z L, LI C H, NG J K Y, et al. Location estimation via support vector regression[J]. IEEE Transactions on Mobile Computing, 2007, 6(3): 311-321. DOI:10.1109/TMC.2007.42 |
 2020, Vol. 46
2020, Vol. 46
