0 概述

随着智能无线设备的不断更新, 人们对其传输速率的要求也越来越高^[1]。大规模多输入多输出(Multiple-Input Multiple-Output, MIMO)中继预编码通信技术因其具有高波束增益^[2], 能够补偿毫米波信道传输中的路径损耗, 且扩大了通信范围, 已成为下一代移动通信的关键技术之一^[3-4]。

当利用大规模天线阵列进行传输时, 采用全数字预编码结构具有高昂的射频链成本^[5]。因此, 具有较少射频链路的混合预编码方案成为大规模MIMO中继预编码技术的研究热点^[6-7]。文献[8]将传统通信网络中混合预编码问题表述为空间稀疏重构问题, 并提出空间稀疏预编码算法, 实现接近全数字预编码的性能。针对部分连接结构的最佳混合预编码问题, 文献[9]分析高信噪比和低信噪比下的优化方案, 并采用注水算法实现最佳混合预编码器。

相比于传统通信, 中继通信在求解最优中继混合预编码矩阵时涉及多变量联合优化, 并且优化约束具有多个非凸条件, 导致直接对中继混合预编码进行设计变得极其复杂。针对具有最小均方误差的中继混合预编码系统, 文献[10]通过将六阶联合优化问题分解成3个二次约束二次优化的子问题, 采用逐次逼近的迭代算法高度近似该问题, 从而求得最优化混合预编码矩阵。针对全双工中继混合预编码系统, 文献[11]通过使用正交匹配追踪理论对存在自干扰的混合预编码矩阵进行干扰消除, 并对能量效率与频谱效率进行联合优化分析。针对存在不完美信道状态信息条件下的中继混合预编码设计问题, 文献[12]利用信道的长期特性, 设计模拟波束形成矩阵, 并推导得出可实现频谱效率的分析界限。上述设计通常假设模拟预编码器的相位是通过使用无限量化精度移相器产生的, 但是现如今的技术无法实现过高量化精度移相器的设计^[13], 并且过高的量化精度需要高昂的硬件成本与功耗^[14-15]。

针对中继节点混合预编码的多阶非凸特性, 为突破因采用过高量化精度移相器所带来的系统硬件限制, 本文提出一种基于有限量化精度移相器的中继混合预编码算法。该算法以最大化系统信息速率为目标, 将中继节点预编码问题描述为空间稀疏重构问题, 并利用离散化正交匹配混合预编码算法进行求解。

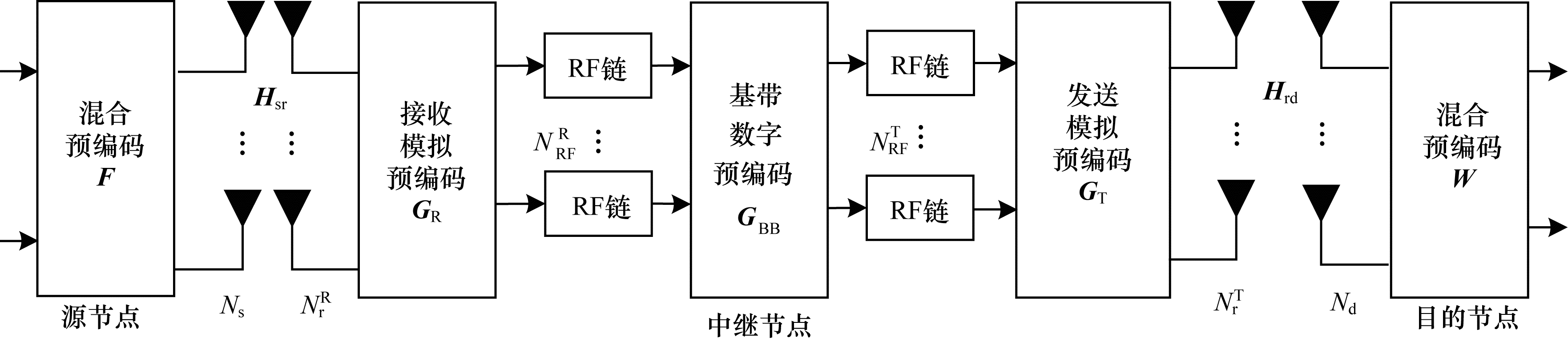
1 系统模型 1.1 中继大规模MIMO系统

本文研究具有单用户与单基站的中继大规模MIMO系统, 全连接的中继混合预编码结构如图 1所示。相比源节点与目的节点, 中继节点的结构更为复杂, 包括接收模拟预编码器G_R、基带数字预编码器G_BB、发送预编码器G_T, 接收端配备N_r^R根天线与N_RF^R个接收RF链, 发送端配备N_r^T根天线与N_RF^T个发送RF链。

源节点使用N_S根天线与N_RF^S个RF链对L_S个数据流进行多流传输, 其中满足L_S≤N_RF^S≤N_S条件。数据流通过混合预编码器F=F_RFF_BB(模拟预编码器F_RF∈${{\mathbb{C}}^{{{N}_{\text{S}}}\times N_{\text{RF}}^{\text{S}}}}$、数字预编码器F_BB∈${{\mathbb{C}}^{N_{\text{RF}}^{\text{S}}\times N_{\text{RF}}^{\text{S}}}}$)进行处理后发送, 中继端接收到的信号表示为:

$ {x_r} = \sqrt {{P_{\rm{r}}}} {\mathit{\boldsymbol{H}}_{{\rm{sr}}}}{\mathit{\boldsymbol{F}}_{{\rm{RF}}}}{\mathit{\boldsymbol{F}}_{{\rm{BB}}}}\mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{n}}_{{\rm{sr}}}} = \sqrt {{P_{\rm{r}}}} {\mathit{\boldsymbol{H}}_{{\rm{sr}}}}\mathit{\boldsymbol{Fs}} + {\mathit{\boldsymbol{n}}_{{\rm{sr}}}} $

(1)

其中, s为发射信号, 满足$\mathbb{E}${ss^H}=I_LS/L_S, H_sr为源节点到中继节点的毫米波信道矩阵, n_sr为满足复高斯分布的噪声矩阵, 即n_sr∈$\mathcal{CN}$(0, σ_sr²I), 混合预编码矩阵满足功率约束${{\left\| \boldsymbol{F} \right\|}_{\text{F}}}^{2}={{L}_{\text{S}}}$。

中继节点将接收到的信号分别通过接收端模拟预编码器G_R∈${{\mathbb{C}}^{N_{\text{r}}^{\text{R}}\times N_{\text{RF}}^{\text{R}}}}$、基带数字预编码器G_BB∈${{\mathbb{C}}^{N_{\text{RF}}^{\text{R}}\times N_{\text{RF}}^{\text{R}}}}$、发送端模拟预编码器G_T∈${{\mathbb{C}}^{N_{t}^{\text{R}}\times N_{\text{RF}}^{\text{R}}}}$进行处理, 通过发射端天线发送至目的节点, 目的节点接收到的信号表示为:

$ {x_{\rm{d}}} = \sqrt {{P_{\rm{d}}}} {\mathit{\boldsymbol{H}}_{{\rm{rd}}}}{\mathit{\boldsymbol{G}}_{\rm{T}}}{\mathit{\boldsymbol{G}}_{{\rm{BB}}}}\mathit{\boldsymbol{G}}_{\rm{R}}^{\rm{H}}{x_{\rm{r}}} + {\mathit{\boldsymbol{n}}_{{\rm{rd}}}} = \sqrt {{P_{\rm{d}}}} {\mathit{\boldsymbol{H}}_{{\rm{rd}}}}G{x_{\rm{r}}} + {\mathit{\boldsymbol{n}}_{{\rm{rd}}}} $

(2)

其中, G=G_TG_BBG_R^H为中继端混合预编码矩阵, H_rd为中继端到目的端毫米波信道矩阵, n_rd为满足复高斯分布的噪声矩阵, 即n_rd∈$\mathcal{CN}$(0, σ_rd²I)。

目的节点采用最小均方误差准则接收, 且与源节点呈对称结构, 即配置N_d根天线与N_RF^d个RF链。用户处理后的信号表示为:

$ y = {\mathit{\boldsymbol{W}}^{\rm{H}}}{x_{\rm{d}}} $

(3)

其中, W=W_RFW_BB为目的端混合预编码器, W_RF∈${{\mathbb{C}}^{{{N}_{\text{d}}}\times N_{\text{RF}}^{\text{d}}}}$为接收模拟预编码器, W_BB∈${{\mathbb{C}}^{N_{\text{RF}}^{\text{d}}\times N_{\text{RF}}^{\text{d}}}}$为接收数字预编码器。

1.2 毫米波信道模型

毫米波信道通常为集群信道, 且具有可由低阶矩阵表示的稀疏结构。本文采用Saleh-Valenzuela信道模型^[16]来体现毫米波通信的信道特性。

源节点至中继节点信道以及中继节点至目的节点信道分别表示为:

$ {{\mathit{\boldsymbol{H}}_{{\rm{sr}}}} = \sum\limits_{l = 1}^{{L_{\rm{h}}}} {{\alpha _l}} \mathit{\boldsymbol{a}}_l^{\rm{R}}(\theta _l^{\rm{R}}){{(\mathit{\boldsymbol{a}}_l^{\rm{S}}(\theta _l^{\rm{S}}))}^{\rm{H}}}} $

(4)

$ {{\mathit{\boldsymbol{H}}_{{\rm{rd}}}} = \sum\limits_{l = 1}^{{L_{\rm{g}}}} {{\gamma _l}} \mathit{\boldsymbol{a}}_l^{\rm{R}}(\beta _l^{\rm{R}}){{(\mathit{\boldsymbol{a}}_l^{\rm{D}}(\beta _l^{\rm{D}}))}^{\rm{H}}}} $

(5)

其中, L_h与L_g为上述两信道传播路径数, α_l与γ_l为各自信道传输过程中的增益, a_l^R、a_l^S、a_l^D为各节点天线阵列响应矢量, θ_l^R、θ_l^S、β_l^R、β_l^D为各自信道发送与接收方位角。

本文采用均匀平面天线阵列, 水平方向具有间距为d_x的N个天线, 其阵列响应矢量表示为:

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{a}}_x^\zeta (\theta ) = }\\ {\frac{1}{{\sqrt {{N_\zeta }} }}{{[1,{{\rm{e}}^{j\frac{{2\pi }}{\lambda }{d_x}{\rm{sin}}(\theta )}},{{\rm{e}}^{j\frac{{4\pi }}{\lambda }{d_x}{\rm{sin}}(\theta )}}, \cdots ,{{\rm{e}}^{j({N_\zeta } - 1)\frac{{2\pi }}{\lambda }{d_x}{\rm{sin}}(\theta )}}]}^{\rm{T}}}} \end{array} $

(6)

其中, λ为波长, ζ∈{S, R, D}为各节点集合。

垂直方向具有间距为d_y的M个天线, 其阵列响应矢量表示为:

$ \mathit{\boldsymbol{a}}_y^\zeta (\theta ) = \frac{1}{{\sqrt {{M_\zeta }} }}{[1,{{\rm{e}}^{j\frac{{2\pi }}{\lambda }{d_y}{\rm{sin}}(\theta )}},{{\rm{e}}^{j\frac{{4\pi }}{\lambda }{d_y}{\rm{sin}}(\theta )}}, \cdots ,{{\rm{e}}^{j({M_\zeta } - 1)\frac{{2\pi }}{\lambda }{d_y}{\rm{sin}}(\theta )}}]^{\rm{T}}} $

(7)

其中, λ为波长, ζ∈{S, R, D}为各节点集合。

2 离散化中继混合预编码方案 2.1 混合预编码矩阵求解

针对中继混合预编码问题, 假设发送的信号满足高斯分布, 并且所有信道状态信息均为已知。结合式(2)和式(3), 毫米波中继大规模MIMO系统的频谱效率可以表示为:

$ \mathit{\boldsymbol{R}} = {\rm{lb}}|{\mathit{\boldsymbol{I}}_{{L_{\rm{S}}}}} + \frac{P}{{{L_{\rm{S}}}}}[{\mathit{\boldsymbol{R}}_{\rm{s}}}] \times {[{\mathit{\boldsymbol{R}}_{\rm{s}}}]^{\rm{H}}} \times \mathit{\boldsymbol{R}}_n^{ - 1}| $

(8)

其中, R_s=W^HH_rdGH_srF为有效接收信号的协方差矩阵, R_n为噪声和干扰的协方差矩阵, 具体表示为R_n=σ²[(W^HH_rdG)(W^HH_rdG)^H+W^HW]。

为了求得最大化的系统频谱效率, 需要将所有的模拟与数字预编码器联合进行设计。模拟预编码器通过使用移相器对相位进行调整, 将移相器的值量化为以δ=2π/2^B为量化单位的具有2^B个有限数量元素的量化集合Φ。该集合表示为:

$ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }} \buildrel \Delta \over = \{ 0,\delta ,2\delta , \cdots ,({2^B} - 1)\delta \} $

(9)

其中, B为最大量化精度。

根据量化移相器的取值, 所有模拟预编码器的恒模约束转变为:

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{Q}} \buildrel \Delta \over = \{ 1,{{\rm{e}}^{j\delta }},{{\rm{e}}^{j2\delta }}, \cdots ,{{\rm{e}}^{j({2^B} - 1)\delta }}\} }\\ {{{(\varGamma )}_{n,m}} \in \mathit{\boldsymbol{Q}}} \end{array}} \right. $

(10)

其中, Γ为所有模拟预编码器的集合。

在系统总功率的约束下, 通过使用量化移相器, 中继混合预编码优化问题可以转化为:

$ \begin{array}{*{20}{l}} {\mathop {{\rm{max}}}\limits_{\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}},\mathit{\boldsymbol{W}}} R(\mathit{\boldsymbol{F}},\mathit{\boldsymbol{G}},\mathit{\boldsymbol{W}})}\\ {{\rm{s}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{tr}} (\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}}) \le {P_{\rm{r}}}}\\ {{\rm{tr}} (\mathit{\boldsymbol{G}}({\mathit{\boldsymbol{H}}_{{\rm{sr}}}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{H}}_{{\rm{sr}}}^{\rm{H}} + \sigma _n^2{\mathit{\boldsymbol{I}}_{{N_d}}}){\mathit{\boldsymbol{G}}^{\rm{H}}}) \le {P_{\rm{R}}}}\\ {{{({\mathit{\boldsymbol{F}}_{{\rm{RF}}}})}_{m,n}} \in \mathit{\boldsymbol{Q}},{{({\mathit{\boldsymbol{W}}_{{\rm{RF}}}})}_{m,n}} \in \mathit{\boldsymbol{Q}}}\\ {{{({\mathit{\boldsymbol{G}}_{\rm{T}}})}_{m,n}} \in \mathit{\boldsymbol{Q}},{{({\mathit{\boldsymbol{G}}_{\rm{R}}})}_{m,n}} \in \mathit{\boldsymbol{Q}}} \end{array} $

(11)

为了求得式(10)中的最大化频谱效率, 需要设计每个节点的混合预编码器。其中, 源节点与目的节点的优化问题为传统点对点优化问题, 其约束条件仅与其自身节点预编码矩阵有关, 而与其他节点的预编码矩阵无关。因此, 可以通过迭代算法来对源节点与目的节点的优化问题进行求解, 如采用文献[17]中提出的基于几何平均分解算法求得源节点与目的节点的混合预编码矩阵F和W。本文将主要针对中继节点的量化进行求解, 不对源节点与目的节点进行赘述。

将联合优化问题式(11)进行解耦, 分离各个节点的恒模约束与功率约束, 其中分离重构后的中继节点优化问题表示如下:

$ \begin{array}{*{20}{l}} {\mathop {{\rm{max}}}\limits_\mathit{\boldsymbol{G}} R = {\rm{lb}}|{\mathit{\boldsymbol{I}}_{{L_{\rm{S}}}}} + \frac{P}{{{L_{\rm{S}}}}}{\mathit{\boldsymbol{R}}_{\rm{s}}}{\mathit{\boldsymbol{R}}^{\rm{H}}}\mathit{\boldsymbol{R}}_n^{ - 1}|}\\ {{\mathop{\rm s}\nolimits} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm t}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm tr} (\mathit{\boldsymbol{G}}({\mathit{\boldsymbol{H}}_{{\rm{sr}}}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{H}}_{{\rm{sr}}}^{\rm{H}} + \sigma _n^2{\mathit{\boldsymbol{I}}_{{N_{\rm{d}}}}}){\mathit{\boldsymbol{G}}^{\rm{H}}}) \le {P_{\rm{R}}}}\\ {{{({\mathit{\boldsymbol{G}}_{\rm{T}}},{\mathit{\boldsymbol{G}}_{\rm{R}}})}_{m,n}} \in \mathit{\boldsymbol{Q}}} \end{array} $

(12)

其中, 目标函数设置为最大化该系统频谱效率, 优化约束为中继节点的功率约束与中继节点模拟预编码器的恒模约束。

针对所分解出的中继端混合预编码优化问题, 由于该优化问题需要同时对3个预编码矩阵进行联合优化, 并且该优化问题同时具有恒模约束与功率约束的非凸约束条件。因此对混合预编码问题分离非凸约束与功率约束, 并基于稀疏近似方法进行求解。暂时不考虑模拟预编码器的量化影响, 并将优化问题转换为范数最小化问题, 具体表示为:

$ \begin{array}{*{20}{l}} {\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{G}} \left\| {{\mathit{\boldsymbol{G}}_{{\rm{opt}}}} - {\mathit{\boldsymbol{G}}_{\rm{T}}}{\mathit{\boldsymbol{G}}_{{\rm{BB}}}}\mathit{\boldsymbol{G}}_{\rm{R}}^{\rm{H}}} \right\|{\kern 1pt} {{\kern 1pt} _{\rm{F}}}}\\ {{\mathop{\rm s}\nolimits} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm t}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm tr} (\mathit{\boldsymbol{G}}({\mathit{\boldsymbol{H}}_{{\rm{sr}}}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{H}}_{{\rm{sr}}}^{\rm{H}} + \sigma _n^2{\mathit{\boldsymbol{I}}_{{N_d}}}){\mathit{\boldsymbol{G}}^{\rm{H}}}) \le {P_{\rm{R}}}}\\ {{\mathit{\boldsymbol{G}}_{\rm{T}}} \in \{ \mathit{\boldsymbol{a}}_l^{{\rm{Rt}}},\forall l\} {\mathit{\boldsymbol{G}}_{\rm{R}}} \in \{ \mathit{\boldsymbol{a}}_l^{{\rm{Rt}}},\forall l\} } \end{array} $

(13)

其中, G_opt为无约束最佳预编码矩阵, a_l^Rt与a_l^Rr为中继节点发送与接收天线响应矢量。定义信道矩阵H_i的奇异值分解为H_i=U_iΣ_iVH_i, i∈{sr, rd}, 其中U_i为左奇异值酉矩阵, V_i为右奇异值酉矩阵, Σ_i为单位的对角矩阵。

将无约束的奇异值分解预编码矩阵G_opt=G_T^optG_R^{opt H}作为目标矩阵, 其中G_T^opt由奇异值分解后的中继到目的端的信道H_rd的右奇异向量构成, G_R^opt由源节点到中继的信道H_sr的左奇异值组成。将模拟预编码矩阵代入, 其问题可以转化表示为^[8]:

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{G}}_{{\rm{BB}}}^{{\rm{opt}}} = \mathop {{\rm{ argmin }}}\limits_\mathit{\boldsymbol{G}} {{\left\| {{\mathit{\boldsymbol{G}}_{{\rm{opt}}}} - {A_{\rm{T}}}{{\mathit{\boldsymbol{\tilde G}}}_{{\rm{BB}}}}A_{\rm{R}}^{\rm{H}}} \right\|}_{\rm{F}}}}\\ {{\mathop{\rm s}\nolimits} .{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm t}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm tr} (\mathit{\boldsymbol{\tilde G}}({\mathit{\boldsymbol{H}}_{{\rm{sr}}}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{F}}^{\rm{H}}}\mathit{\boldsymbol{H}}_{{\rm{sr}}}^{\rm{H}} + \sigma _n^2{\mathit{\boldsymbol{I}}_{{N_d}}}){{\mathit{\boldsymbol{\tilde G}}}^{\rm{H}}}) \le {P_{\rm{R}}}}\\ {\left\| {{\rm{diag}} ({{\mathit{\boldsymbol{\tilde G}}}_{{\rm{BB}}}}\mathit{\boldsymbol{\tilde G}}_{{\rm{BB}}}^{\rm{H}})} \right\|{{\kern 1pt} _0} = N_{{\rm{RF}}}^{\rm{R}}} \end{array} $

(14)

其中, $\tilde{\boldsymbol{G}}=\boldsymbol{A}_{\mathrm{T}} \tilde{\boldsymbol{G}}_{\mathrm{BB}} \boldsymbol{A}_{\mathrm{R}}^{\mathrm{H}}$, A_T与A_R为天线阵列响应向量矩阵的辅助矩阵, 稀疏约束$\left\|\operatorname{diag}\left(\tilde{\boldsymbol{G}}_{\mathrm{BB}} \tilde{\boldsymbol{G}}_{\mathrm{BB}}^{\mathrm{H}}\right)\right\|_{0}=N_{\mathrm{RF}}^{\mathrm{R}}$表示${{\widetilde{\mathrm{G}}}_{\text{BB}}}$是由G_BB组成的具有N_RF^R个非零行的稀疏矩阵。

通过优化式(13)可以求得最佳数字预编码矩阵与最佳模拟预编码矩阵, 然而所求得的模拟预编码矩阵仍基于无限量化精度移相器, 因此需要对模拟预编码器进行量化。定义量化函数为:

$ {\hat \tau _{n,m}} = Q({\tau _{m,n}}) = \left( {\mathop {{\rm{minimize}}}\limits_{\zeta \in \{ 0,1, \cdots ,{2^B} - 1\} } |{\tau _{m,n}} - \zeta \delta |} \right)\delta $

(15)

其中, ${{\widehat{\tau }}_{m, n}}$为τ_{m, n}的量化值, 量化器Q将输入的τ_{m, n}量化为距离量化集合Φ最近的一个点后并输出量化值${{\widehat{\tau }}_{m, n}}$。将模拟预编码器的每一个元素分别通过量化器, 以此得到量化后的模拟预编码矩阵。

2.2 离散化正交匹配算法

与文献[18]不同, 中继混合预编码稀疏近似问题具有两个天线阵列响应矩阵, 并且需要对其进行联合求解。本文提出的求解算法主要步骤如下:

输入  H_srH_rd

输出  G_TG_BBG_R^H

步骤1 将接收天线响应矩阵A_R中与残差矩阵G最相关的行r赋值于接收模拟预编码矩阵G_Rⁿ。

步骤2 根据式(14)对获取的接收模拟预编码矩阵G_Rⁿ中每个元素进行量化处理, 并重构G_Rⁿ。

步骤3 将发送天线响应矩阵A_T与接收模拟预编码矩阵G_Rⁿ和残差G共同相关的列c赋值于发送模拟预编码矩阵G_Tⁿ。

步骤4 通过与接收端相同的量化方式对G_Tⁿ进行量化。

步骤5 根据最小二乘法原理对数字预编码矩阵进行求解。

步骤6 通过计算无约束预编码器与混合预编码器之间的归一化距离来对残差进行更新。

步骤7 对功率约束进行设计。

2.3 算法时间复杂度

本文算法通过步骤2、步骤4进行迭代求解, 其中步骤2的时间复杂度为${{T}_{\text{r}}}=O\left({{2}^{{{{\hat{B}}}_{\text{r}}}}}N_{\text{r}}^{\text{R}}{{{\hat{N}}}_{\text{RF}}} \right)$, 步骤4的时间复杂度为$T_{\mathrm{t}}=O\left(2^{\hat{B}_{t}} N_{t}^{\mathrm{R}} \hat{N}_{\mathrm{RF}}\right)$。通过利用步骤1与步骤3进行外部迭代, 其功能是将模拟预编码矩阵中每一列进行单独投影计算, 其复杂度为$O({{\widehat{N}}_{\text{RF}}}\times \text{max}({{T}_{\text{r}}}, {{T}_{\text{t}}}))$。综合计算步骤1~步骤4的时间复杂度, 则系统总的时间复杂度为$O\left(2^{\hat{B}} \hat{N} \hat{N}_{\mathrm{RF}}^{2}\right)$, 其中$\hat{B}=\text{max}\left({{{\hat{B}}}_{\text{r}}}, {{{\hat{B}}}_{\text{t}}} \right)$为中继接收端与发送端之间最大量化精度, $\hat{N}$=max(N_r^R, N_t^R)为中继接收端与中继发送端之间的最大天线数量。

相比于文献[7]中全精度混合预编码算法, 本文算法增加了量化处理, 因此在时间复杂度方面略有增加, 但是系统的能量效率却得到了显著提升。

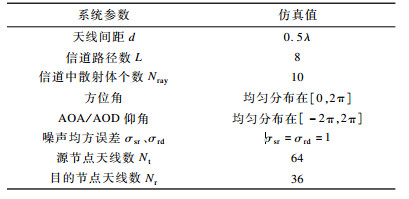
3 仿真分析

为了验证本文提出的离散化中继混合预编码算法的有效性, 通过MATLAB对该系统的频谱效率进行仿真分析。由于在毫米波信道中无约束的全数字预编码器能够达到系统的最佳性能, 因此将使用全数字预编码器^[19]作为仿真对比的上限。假设系统的所有信道增益均符合高斯分布。采用1.2节中的信道环境进行传输, 信道参数设置如表 1所示。

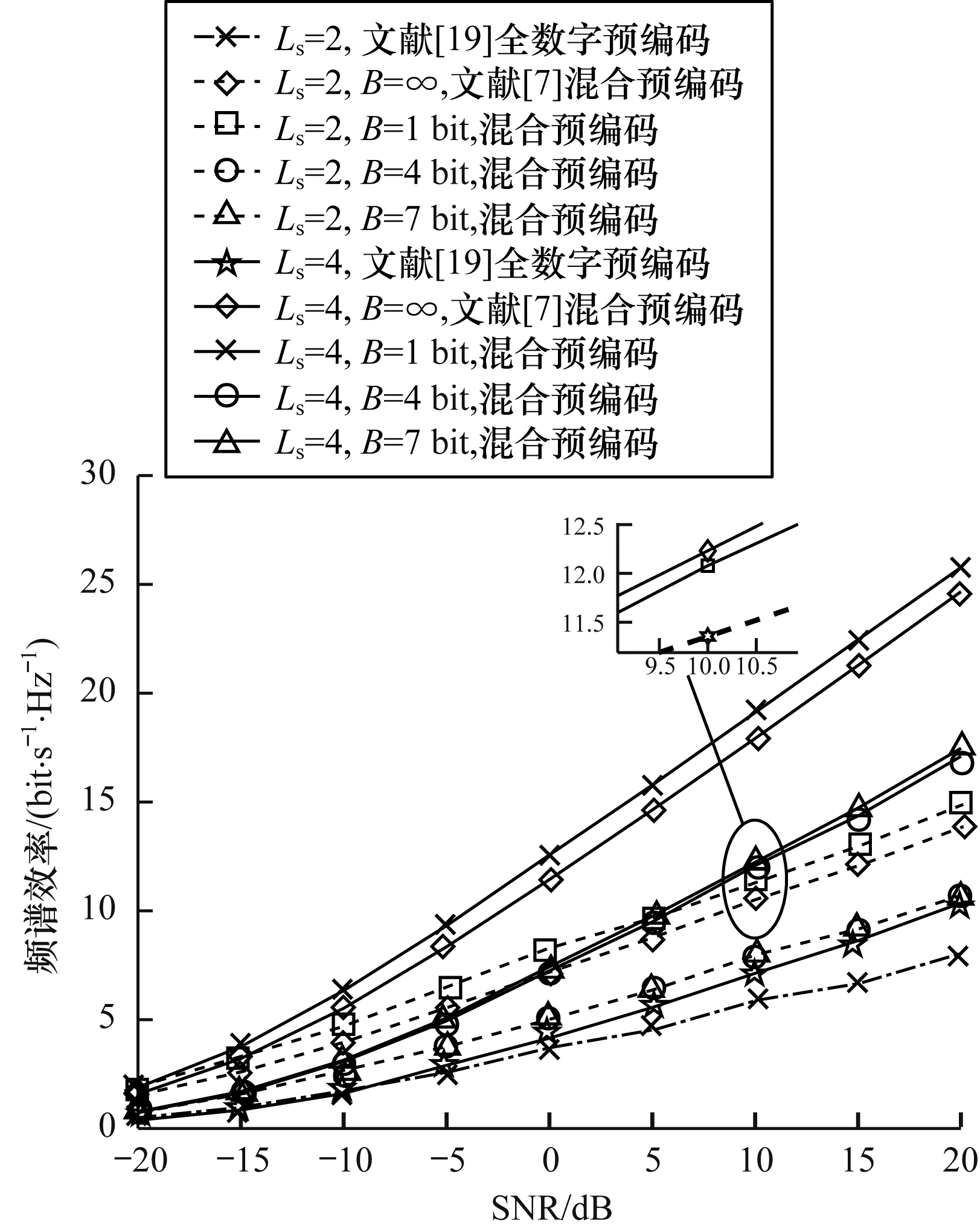
图 2为输入不同信噪比(Signal to Noise Ratio, SNR)情况下, 不同数据流中不同量化精度的中继混合预编码频谱效率的变化曲线, 其中中继节点发送端与接收端采用同一量化精度。由图 2可知, 当数据流L_s一定时, 随着量化精度B的提高, 系统的频谱效率也越来越高, 但当量化精度B增大至4 bit后, 频谱效率将不会大幅度增长。同时, 增加数据流数L_s能够明显地提升系统的频谱效率。因此得益于量化预编码算法通过每次迭代对量化所造成的性能损耗进行了补偿, 混合预编码器采用较低量化精度移相器就能够达到最大化的量化频谱效率。由于中继节点混合预编码器需要同时对中继接收端和发送端进行量化处理, 因此量化后的混合预编码器与不进行量化的混合预编码器的效果存在一定的差距。

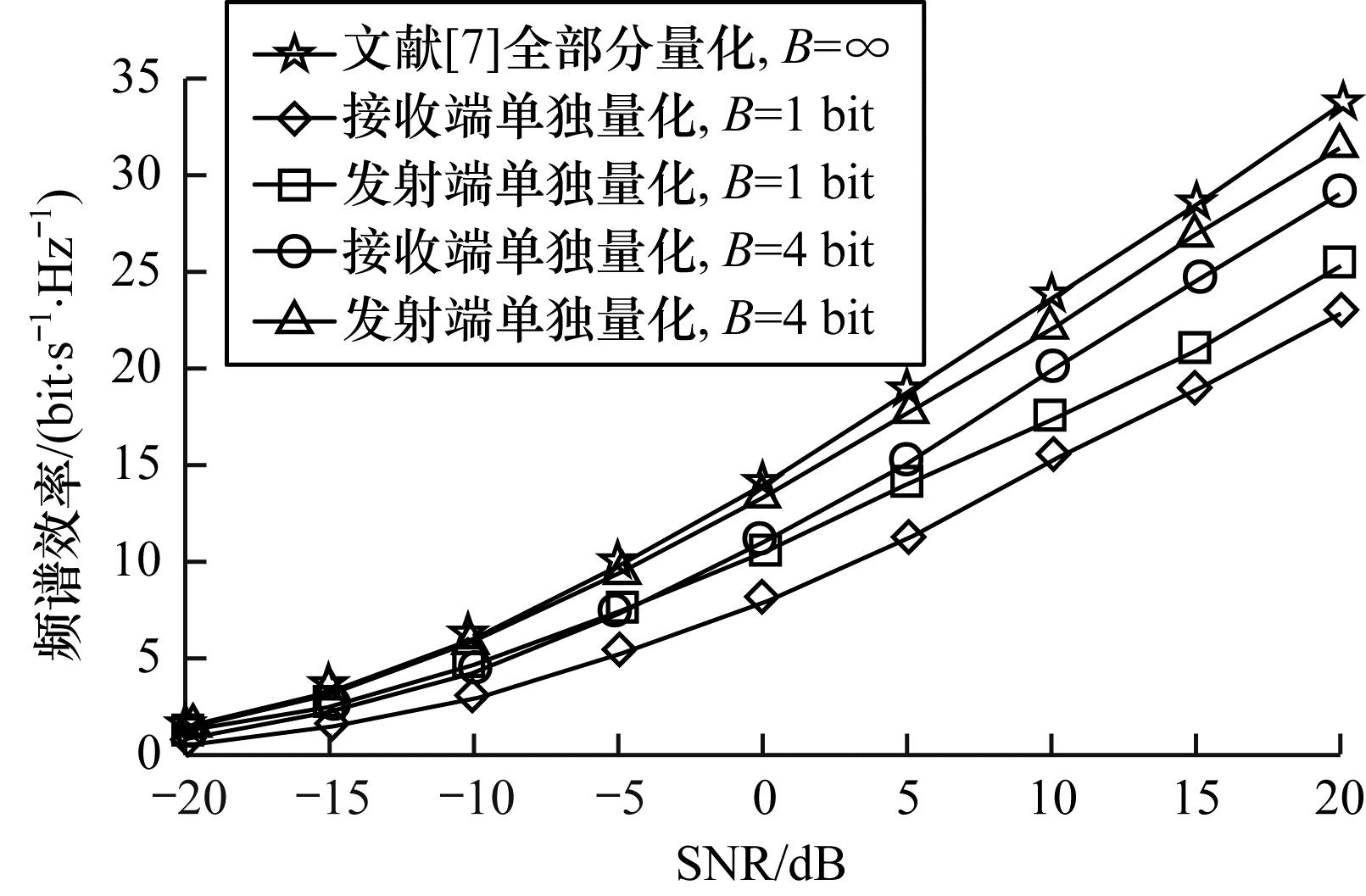
图 3为数据流L_s与RF链数量一定时, 中继接收端与中继发送端单独进行量化时频谱效率随着SNR的变化曲线。由图 3可以看出, 当采用同样量化精度时, 量化后的接收端比量化后的发送端对频谱效率的影响更大。同时, 从单独量化的发送端来看, 当量化精度B为1 bit时, 其频谱效率与无限精度的混合预编码器存在一定的差距, 并且当量化精度为4 bit时, 其频谱效率较为接近无限精度的混合预编码器。当对中继节点的混合预编码器进行求解时, 需要先对接收端进行量化求解, 而发送端是根据量化后的接收端所进行的优化, 并且通过迭代求解将量化损耗降为更低, 因此后进行量化求解的发送端具有较少的量化损耗。

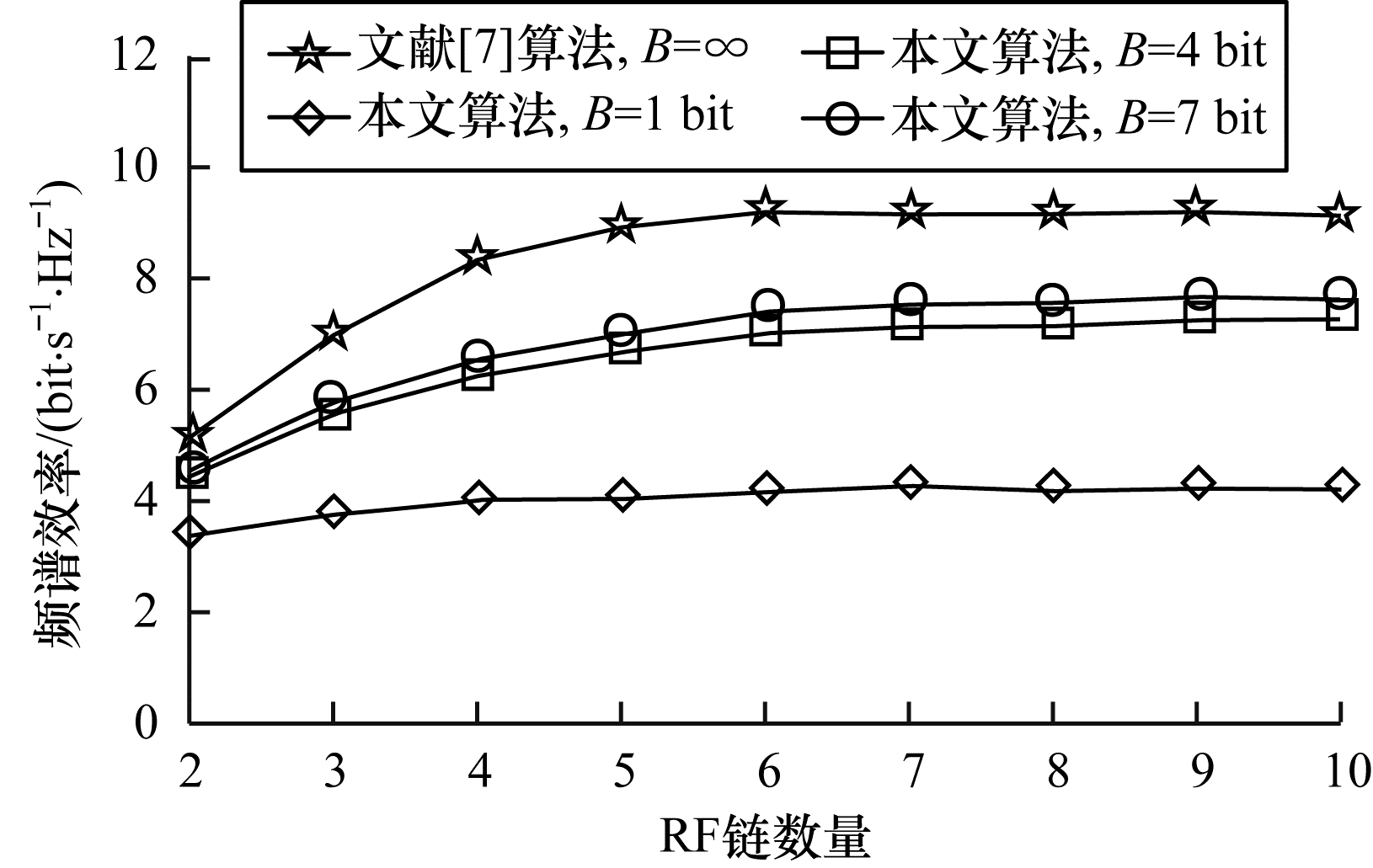
图 4为在不同量化精度下, 使用不同数量的RF链对系统频谱效率的影响, 其中系统SNR为0^[20], 数据流L_s=2, 中继接收端与发送端采用相同数量的RF链。由图 4可知, 当RF链的数量小于5个时, 不同量化精度的离散化中继预编码的频谱效率均随着RF链的增加而呈现增大趋势。同时, 当RF链的数量由2个增加至3个时, 系统的频谱效率增加显著。此外, 当RF链的数量增加至一定数值后, 系统的性能逐渐稳定, 继续增加RF链的数量时, 系统性能不会继续提高, 并且功耗反而增多。

图 5为在不同量化精度下, 使用不同数量的天线情况对系统频谱效率的影响, 其中数据流L_s=8, 中继发送端与中继接收端采用相同数量的RF链与天线。由图 5可以看出, 当天线的数量小于50根时, 不同量化精度下离散化中继混合预编码的频谱效率均随着天线数量的增加而呈现快速增长趋势, 并且当天线数量增加至一定数量后, 系统的性能逐渐稳定。同时, 当量化精度B达到4 bit时, 中继混合预编码的频谱效率接近于使用高量化精度的频谱效率, 继续提高量化精度不能显著增加系统频谱效率。因此, 当系统无法通过增加量化精度提高性能增益时, 可以增加天线数量来提高系统性能。

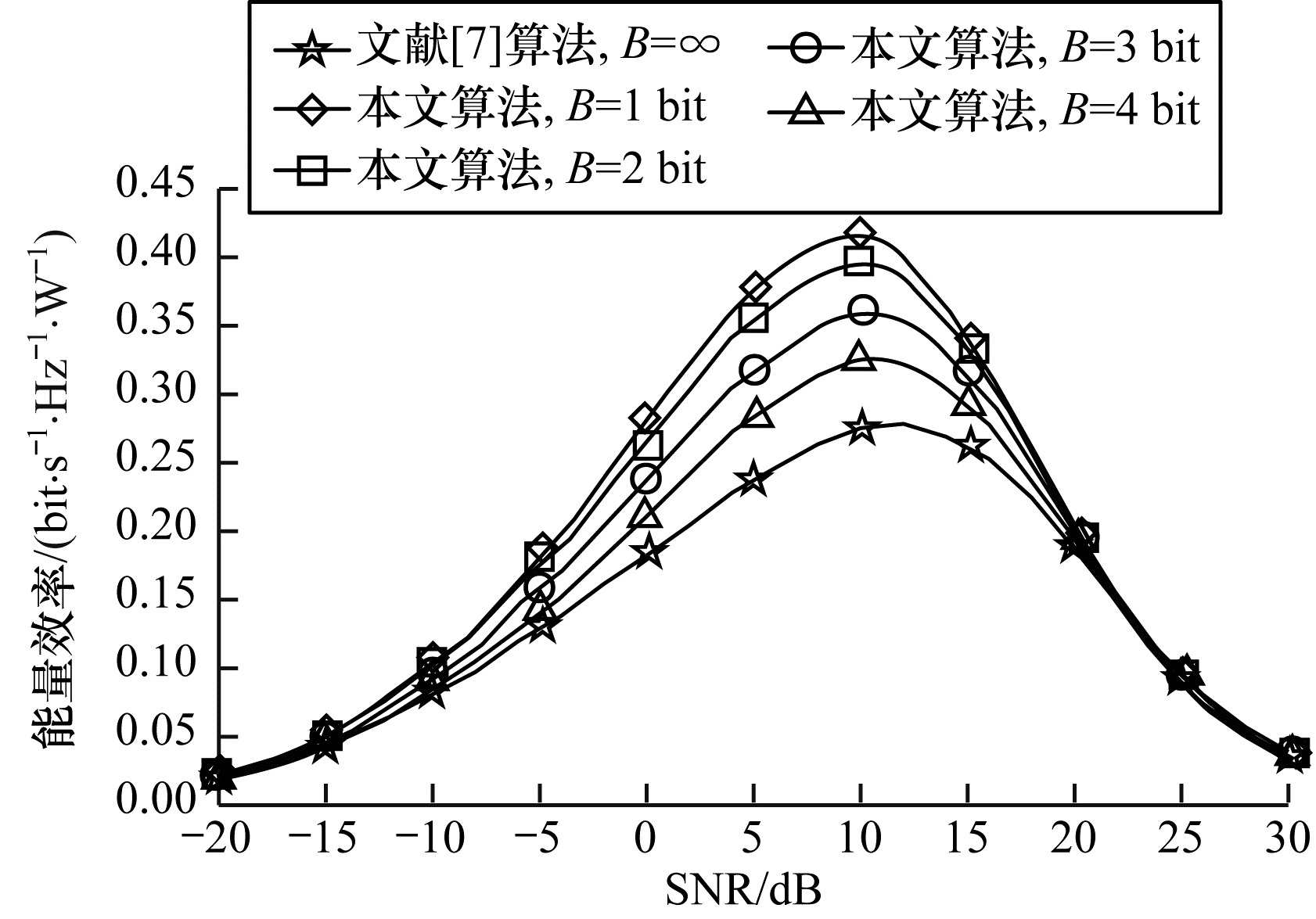
图 6为不同量化精度下中继混合预编码的能量效率随着平均SNR的变化曲线, 采用文献[21]中的功耗参数。由图 6可知, 具有低量化精度的中继混合预编码具有较高的能量效率, 但是随着量化精度的增加, 系统能量效率逐渐减小。同时, 当SNR接近10 dB时, 该系统具有能量效率峰值。

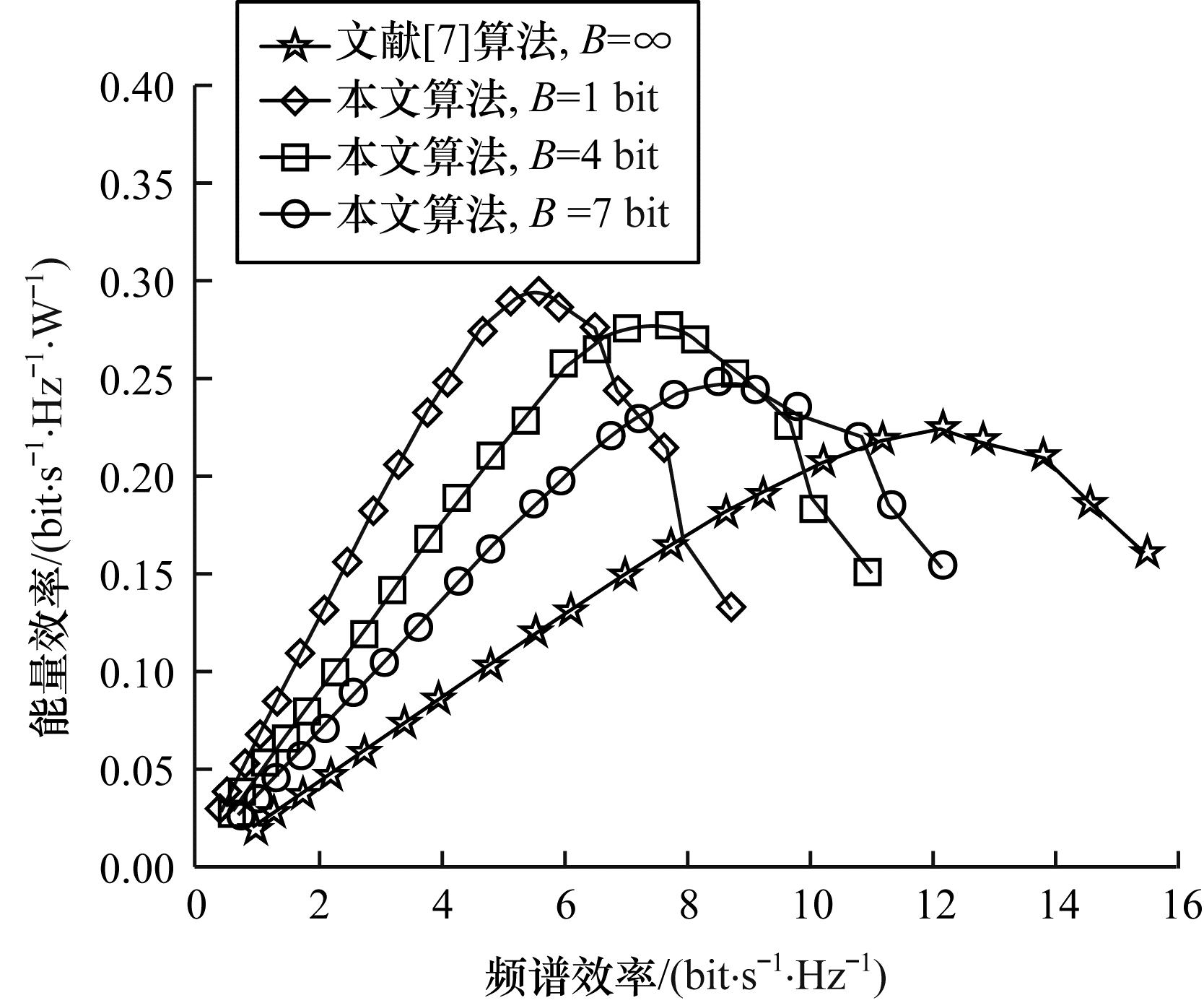
图 7为输入不同SNR条件下, 不同量化精度的中继混合预编码的能量效率与频谱效率的均衡变化曲线。从图 7可以看出, 不同量化精度下混合预编码的能量效率与频谱效率变化趋势相同, 量化精度越低的混合预编码具有越高的能量效率, 但其频谱效率相对较低。随着频谱效率的不断增加, 能量效率将达到峰值, 但是当继续小幅度增加频谱效率时, 能量效率却大幅度下降。当系统频谱效率增加至11 bit/s/Hz时, 量化精度B为4 bit时的中继混合预编码的能量效率接近全精度量化的峰值能量效率, 同时其频谱效率也较为接近全精度量化时的频谱效率。因此, 当采用较低量化精度移相器时, 在牺牲频谱效率的前提下能够获得较大的能量效率。综合考虑中继混合预编码的频谱效率与能量效率, 本文采用较低量化精度的移相器能够使中继混合预编码在具有最大能量效率的同时获得相对较大的频谱效率。

4 结束语

针对毫米波中继大规模MIMO系统, 本文提出一种基于离散化正交匹配追踪的中继混合预编码算法。将中继预编码系统的复杂优化问题解耦为单独节点优化问题, 采用稀疏近似方法分离优化问题中的非凸约束, 再利用离散化正交匹配追踪算法对中继节点混合预编码矩阵进行量化求解。将本文算法与全数字预编码和无限精度正交匹配追踪算法进行对比, 仿真结果表明, 本文算法能够在使用较低量化精度的条件下达到接近最优化的性能, 并且中继节点接收端需使用较高精度量化来抵消量化损耗, 同时发送端使用较低精度量化就能达到最优性能。下一步考虑将该算法推广至不完美信道环境下的中继通信网络, 使其在复杂通信网络中具有更强的适用性。