自从2012年Hinton团队的深度卷积神经网络AlexNet在ImageNet挑战赛上获得冠军后[1],深度学习技术得到快速发展,各种针对语音识别和图像分类任务的新型深度网络被不断提出并取得了很好的处理效果,而基于深度学习技术的通信信号调制识别方法也成为当前国内外的研究热点。文献[2]对基于手工特征与卷积神经网络(Convolutional Neural Network,CNN)提取特征的通信信号调制识别方法进行比较,实验结果证明了CNN对于信号特征有较强的表征能力。文献[3]对通信信号进行预处理后将时频图作为CNN的样本输入,该方法取得了较好的识别效果。文献[4]将手工特征与CNN提取特征相融合,提高了低信噪比条件下的信号识别准确率。然而传统基于CNN的深度学习方法存在对训练样本需求量大的问题,在很多无法提供足够丰富样本量的应用场景下,深度学习网络无法进行有效收敛,导致其在小样本条件下的通信信号调制样式识别中受到了一定的限制。
目前,研究人员通常使用数据增强、基于迁移学习的元学习以及度量学习等方法解决小样本学习[5]问题。数据增强方法通过扩充训练样本集[6]和构造特征[7-8]来有效缓解过拟合现象,但由于生成的样本或构造的特征相似度较高无法完全解决过拟合问题。基于迁移学习的元学习方法[9-11]通过迁移其他任务上的权值网络实现小样本条件下新任务的快速学习,常用方法包括学习最优的初始化条件、迁移梯度更新策略或通过循环神经网络(Recurrent Neural Network,RNN)构建外部存储器。这些基于迁移学习的元学习方法方法虽取得了较为理想的分类效果,但也存在一定的局限性,如使用RNN记忆单元导致算法复杂度高。度量学习方法[12-14]通过特征提取模块将样本映射至低维特征空间中,在特征空间中对特征进行度量并利用最近邻分类器实现分类识别[15-17],其中最具代表性的度量学习方法为VINYALS提出的基于匹配网络的度量学习方法[13],该方法利用注意力机制在支持集上通过嵌入网络预测测试集类别,在训练过程中使用加权平均法对支持集的小样本数据进行分段抽样以模拟测试任务,整体识别效果较好,但是其复杂度随着样本类别的增多而增大。SNELL利用归纳偏置思想提出原型网络[14],在特征空间中以类内的样本均值作为该类的原型表达,通过计算待测样本与类原型之间的距离进行分类。原型网络相比匹配网络算法复杂度有所降低,但由于未考虑类内样本存在偏差时学习到的类原型不够准确,因此导致识别误差较高。本文根据度量学习方法,借鉴原型网络思想,提出一种基于深度级联孪生神经网络的小样本调制识别算法。
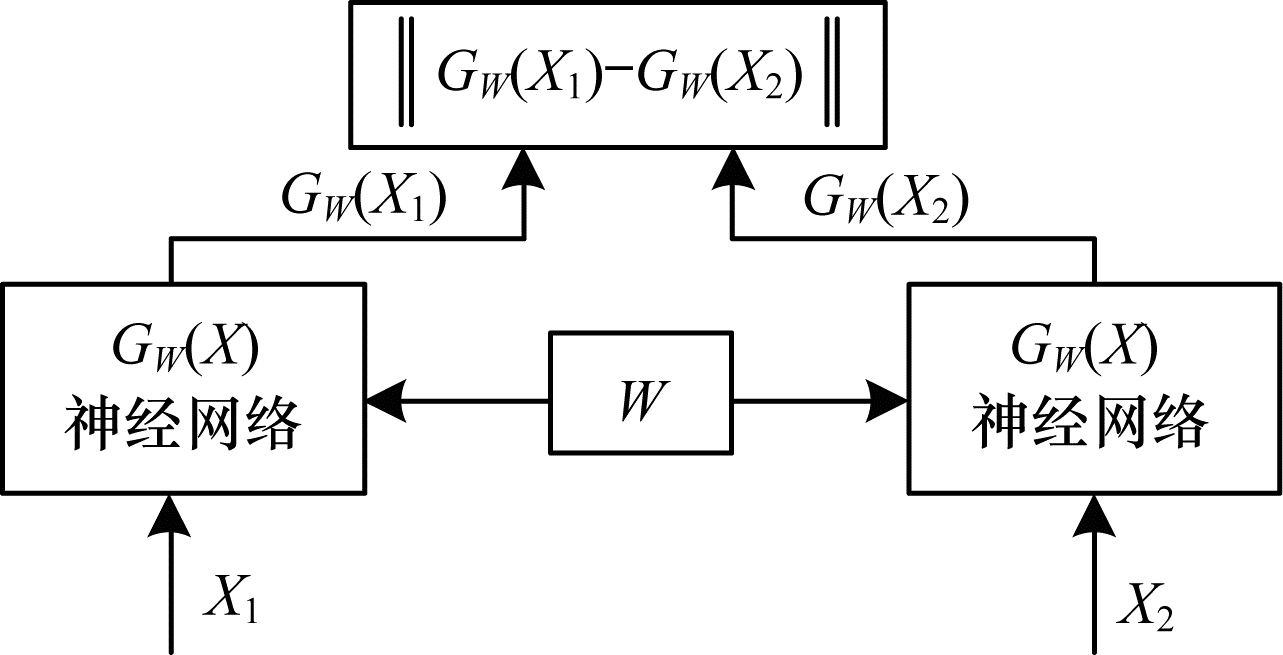
1 孪生神经网络 1.1 孪生神经网络结构孪生神经网络系统[17-18]由一对孪生的子神经网络构成,这两个子神经网络之间共享权值与偏置等参数,输入为一对样本。通过神经网络提取该对样本的特征向量,即将输入映射至目标空间,在孪生神经网络后端计算提取到的特征向量的距离度量,通过该距离来度量输入的一对样本之间的相似度。孪生神经网络结构如图 1所示,其中,
|
Download:
|
| 图 1 孪生神经网络结构 Fig. 1 Structure of Siamese neural network | |
在训练阶段,通过将训练样本对输入至两个权值共享的子神经网络中,利用反向传播算法调节网络权值W,使用最小化损失函数值学习优化模型的所有参数,即当
为最小化相同类别之间的距离度量且最大化不同类别之间的距离度量,定义损失函数如式(1)所示:
| $ L(W, y)=\frac{1}{2}(1-y){E}_{W}^{2}+\frac{1}{2}y\left[\mathrm{m}\mathrm{a}\mathrm{x}\right(0, d-{E}_{W}{\left)\right]}^{2} $ | (1) |
其中:d为阈值约束,用于选取适合网络训练的异类样本对;y为类别因子,定义为
为使损失函数最小化,使用随机梯度下降算法优化神经网络参数
| $ {L}_{\mathrm{S}}(W, y)=\frac{1}{2}{E}_{W}^{2} $ | (2) |
参数优化更新过程为:
| $ {W}^{k}={W}^{k}-\mu {E}_{W}\frac{\partial {E}_{W}}{\partial {W}^{k}} $ | (3) |
| $ {b}^{k}={b}^{k}-\mu {E}_{W}\frac{\partial {E}_{W}}{\partial {b}^{k}} $ | (4) |
其中,
| $ {L}_{\mathrm{D}}(W, y)=\frac{1}{2}\left[\mathrm{m}\mathrm{a}\mathrm{x}\right(0, d-{E}_{W}{\left)\right]}^{2} $ | (5) |
当输入的不同类别样本对的距离
| $ {W}^{k}={W}^{k}-\mu (d-{E}_{W})\frac{\partial {E}_{W}}{\partial {W}^{k}} $ | (6) |
| $ {b}^{k}={b}^{k}-\mu (d-{E}_{W})\frac{\partial {E}_{W}}{\partial {b}^{k}} $ | (7) |
孪生神经网络的优化目标是通过对权重矩阵与偏置的不断更新,在最小化损失函数
若利用小样本数据训练基于cross-entropy的神经网络分类器,则会由于神经网络分类器中参数量过大导致分类结果过拟合或者由于训练样本过少导致训练欠拟合,而K-近邻、K-means等非参数化识别方法无需优化参数,通过对样本间的分布距离进行建模,使得同类样本之间的距离更近,而异类样本之间的距离更远,其中典型的非参数化识别方法为度量学习方法,其通过特征提取模块将原始信号特征映射至特征空间,然后在特征空间中通过最近邻分类器进行小样本分类识别。
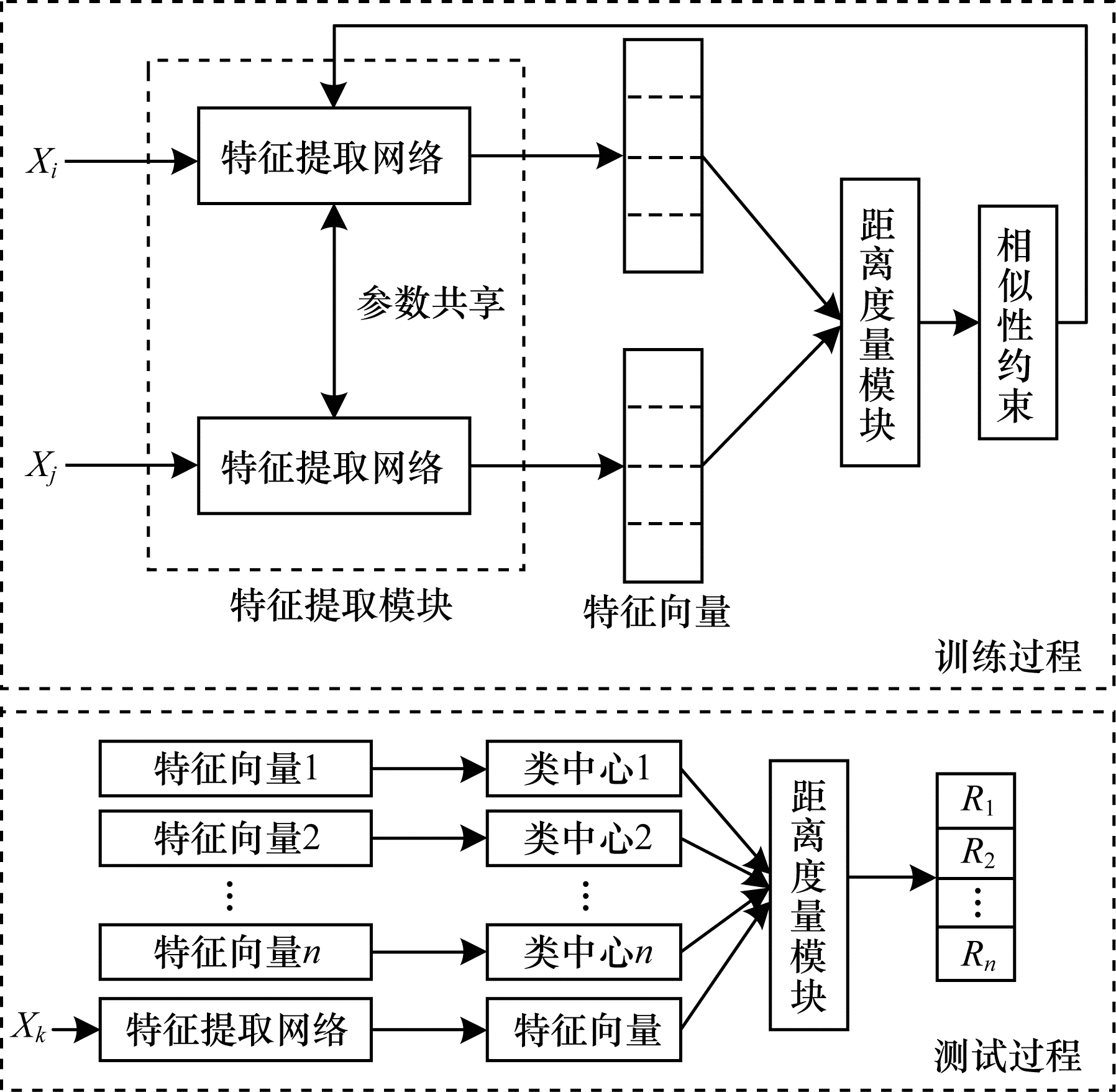
现有度量学习方法的特征提取模块设置相对简单,通常由卷积层堆叠而成,导致特征提取不够完善。本文针对通信信号IQ路时序图的图像空间特性与信号时序特性,设计由CNN和长短时记忆(Long Short Term Memory,LSTM)网络级联的特征提取模块CLS,提取更具代表性的特征并在孪生网络架构下对提取的特征进行距离度量,以相似性约束训练网络并使特征提取网络收敛。本文算法实现过程分为训练过程和测试过程,算法框架如图 2所示,其中:Xi和Xj为训练样本对输入;Xk为测试样本;R1、R2和Rn为测试样本与不同训练样本类别之间的相似度。在测试过程中将训练样本通过特征提取模块提取的特征向量生成各个类别的类中心,然后将通过特征提取网络的待测样本分别与各个类别的类中心输入至距离度量模块生成相似度,最终选取相似度最高的类别作为待测样本的类别。
|
Download:
|
| 图 2 本文算法框架 Fig. 2 Framework of the proposed algorithm | |
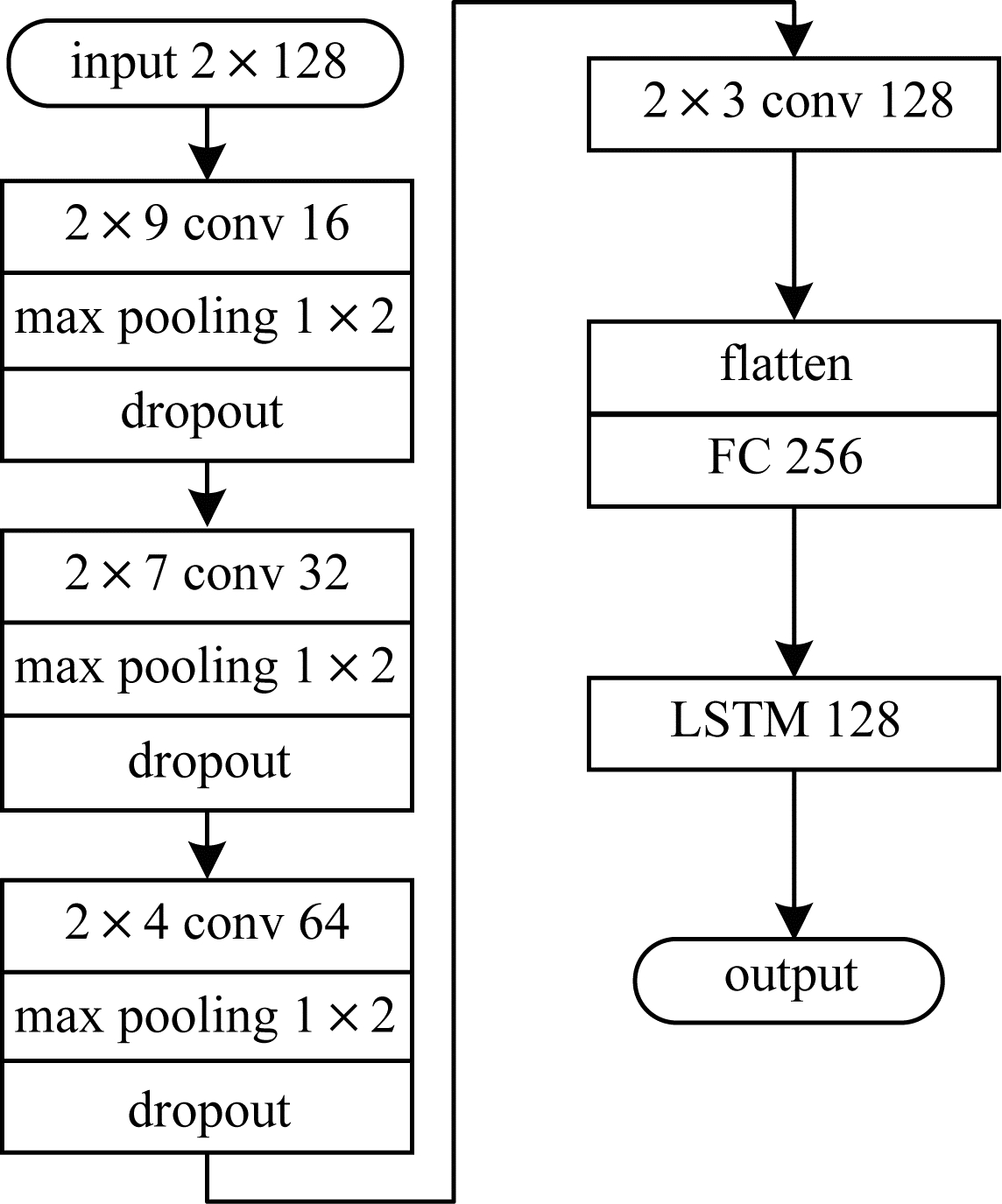
本文在DeepSig公开调制数据集[19]上进行实验,该数据集是通过对信号进行预处理后得到的2×128同相分量I路和正交分量Q路时序图,将其作为特征提取网络的输入,特征提取模块由CNN与LSTM级联而成,具体结构如图 3所示。
|
Download:
|
| 图 3 特征提取模块 Fig. 3 Feature extraction module | |
由于本文算法在小样本条件下实现,网络结构设置不宜过深,因此卷积神经网络由4个卷积层(conv)、3个最大池化层(max pooling)和1个全连接层(FC)组成。根据通信调制信号IQ时序图的稀疏特性,同时为避免卷积核选取过大而增加计算复杂度,选择2×9、2×7、2×4、2×3尺寸的卷积核;在卷积层后添加1个最大池化层,对卷积结果进行非线性下采样,可有效解决卷积层参数误差而引起的均值偏移问题;每层卷积神经网络的输出均采用ReLU激活函数,能有效增加模型的非线性特性,有助于网络模型更好地挖掘样本数据特征。由于每通过1个最大池化层,下一层卷积核数量就会出现倍增,因此将卷积滤波器数量设置为16的倍数。当卷积层输出后,利用flatten层将卷积神经网络提取到的特征输出至具有256个神经元的全连接层,并通过LSTM输出特征。为避免网络训练过程中出现过拟合现象,在每个最大池化层后设置1个dropout层。
2.3 距离度量模块距离度量模块可通过训练使相同类别之间的距离更近而不同类别之间的距离更远,常用的距离度量函数主要包括欧氏距离、马氏距离和余弦相似度度量函数,但此类固定距离度量函数需要嵌入特征提取模块并将样本特征准确地提取至目标子空间。本文通过深度神经网络与特征提取模块联合训练非线性度量函数度量样本之间的相似度。
将特征提取模块输出的特征向量并联后输入至由两个卷积层和两个全连接层组成的距离度量模块(如图 4所示),每个卷积模块后通过最大池化层进行下采样,网络训练同样采用ReLU激活函数激活和dropout层防止网络训练过拟合,最终通过Sigmoid函数将相似度映射至(0,1),计算得到相似度为:
| $ {R}_{i, j}=g\left(c\right(f\left({X}_{i}\right), f\left({X}_{j}\right)\left)\right) $ | (8) |

|
Download:
|
| 图 4 距离度量模块 Fig. 4 Distance measurement module | |
其中,
为同时满足孪生网络中特征提取模块和距离度量模块的约束条件,定义损失函数为:
| $ {L}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=y[{(1-R)]}^{2}+(1-y\left)\right[\mathrm{m}\mathrm{i}\mathrm{n}{(0, d-R)]}^{2} $ | (9) |
由式(9)可知,约束超过相似度阈值的样本对在训练过程中不进行梯度更新,使得网络收敛速度更快。
2.4 算法实现过程本文算法采取测试与训练分离的方法,在训练过程中,通过将相同类别与不同类别的训练样本IQ时序图随机进行两两配对并打上“1”和“0”标签,使相同类别的样本之间更近而不同类别样本之间的距离更远。在测试过程中,借鉴原型网络[14]思想,对于每种调制类别,在特征映射空间中选取最集中的100个训练样本的特征均值作为该类的类别中心,然后使用距离度量模块度量待测样本与类中心之间的相似度,选取具有相似度最高的类中心的类别作为识别类别。本文算法步骤具体为:
步骤1 标签制作。将通信信号IQ路时序图按照相同类别与不同类别进行重新组合,将相同类别的一组图片标签设置为“1”,不同类别的一组图片标签设置为“0”。
步骤2 训练样本对的特征映射。将制作好标签的信号样本对输入至特征提取模块,提取最后一层的LSTM输出作为样本的特征映射。
步骤3 相似度度量。将输出的样本对特征并联后输入至距离度量模块进行相似度度量,并根据损失函数对算法模块进行训练。
步骤4 在测试集中进行类别识别验证。网络训练完成后将待测样本输入到网络中提取特征,并将其与各个类中心的特征通过距离度量模块进行相似度度量,选择相似度最高的类别作为待测样本类别。
3 实验与结果分析 3.1 实验数据集与环境实验采用DeepSig调制识别公开数据集,该数据集中包含8PSK、AM-SSB、BPSK、CPFSK、GFSK、PAM4、QAM16、QAM64、QPSK、WBFM 10种调制样式。在信噪比为-4 dB~18 dB的条件下,每种调制样式的训练样本数量分别为240、360、480、600、720、840、1 200和1 800,测试样本数量为100。实验硬件平台为基于Windows7、32 GB内存和NVDIA P4000显卡的计算机,并通过Python中的Keras开源人工神经网络库完成网络的搭建、训练与测试。
3.2 实验参数设置在模型优化过程中选取Adam[20]优化算法,其相较随机梯度下降算法具有更快的收敛速度和更高的算法稳定性。实验中的优化算法采用超参数默认设置,并设置初始学习率和最小学习率分别为10-3和10-5,当验证损失值增加到10%以上时学习率减少一半,此时选取验证集损失值最低的模型作为最终训练模型。对于实验中损失函数阈值的设置,首先选取初始值为0.1,每次递增0.1,以此递增至0.9,分别记录每个阈值条件下的识别性能,当阈值为0.4时识别效果最佳,因此实验均在损失函数阈值为0.4的条件下进行。在训练过程中为避免出现过拟合现象,本文采用提前终止迭代(Early Stop Iteration,ESI)算法[21]使模型收敛至验证集损失值最低点。
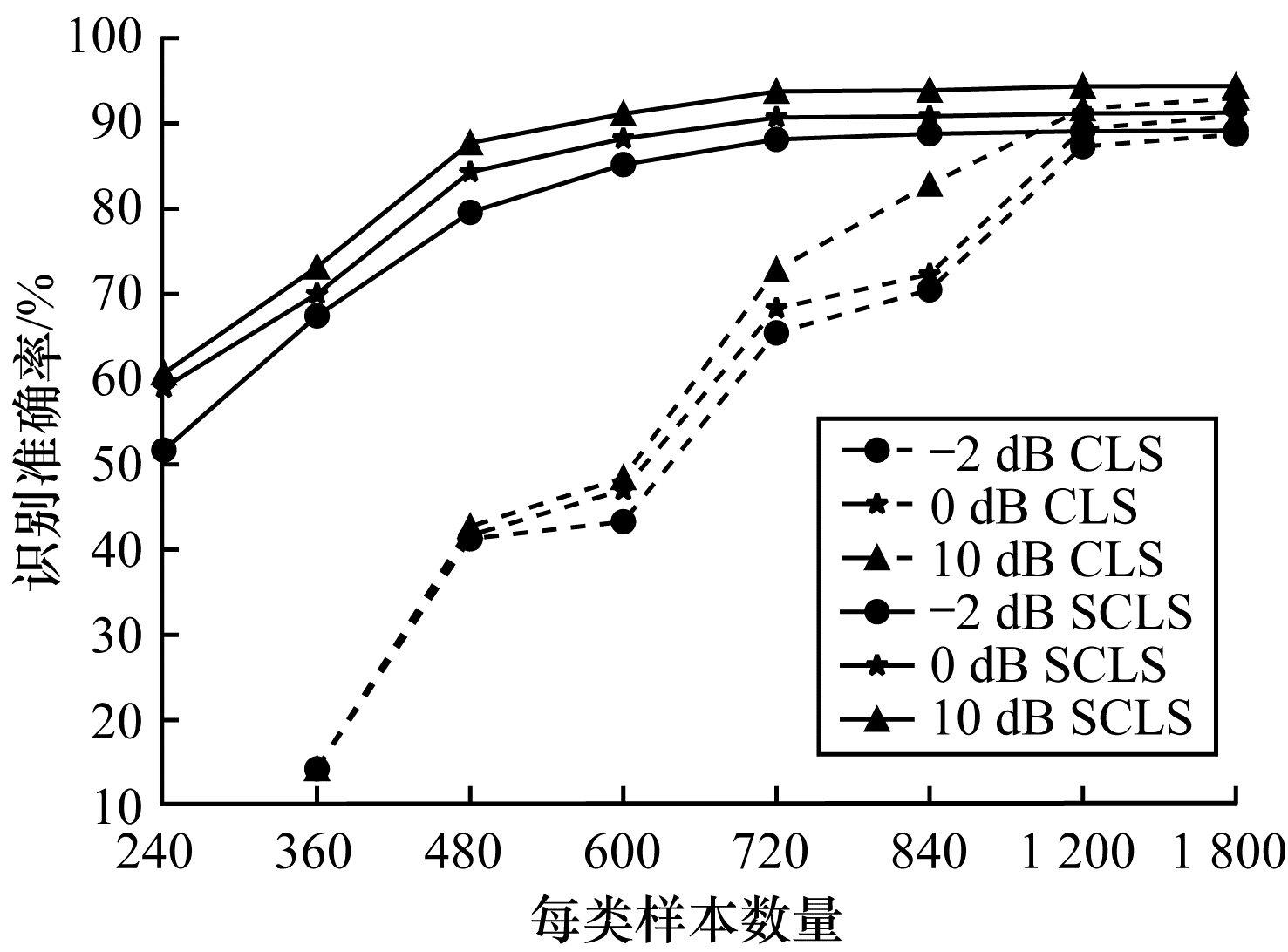
3.3 算法性能分析 3.3.1 孪生神经网络对识别性能的影响为验证在小样本条件下孪生神经网络的作用及其对训练样本数量的需求,训练样本数量分别设置为240、360、480、600、720、840、1 200和1 800,在CLS和孪生CLS(简称SCLS)网络结构下对比信噪比取-2 dB、0 dB和10 dB时调制信号,测试其识别准确率,实验结果如图 5所示。可以看出,SCLS网络结构在训练过程中所需的样本量明显降低,在小样本条件下的识别性能更好,并且当每类调制信号的样本数量为720时,基于SCLS网络结构的调制识别算法的识别准确率基本达到最优。
|
Download:
|
| 图 5 孪生网络结构在小样本条件下的识别性能 Fig. 5 Recognition performance of Siamese network structure under small sample conditions | |
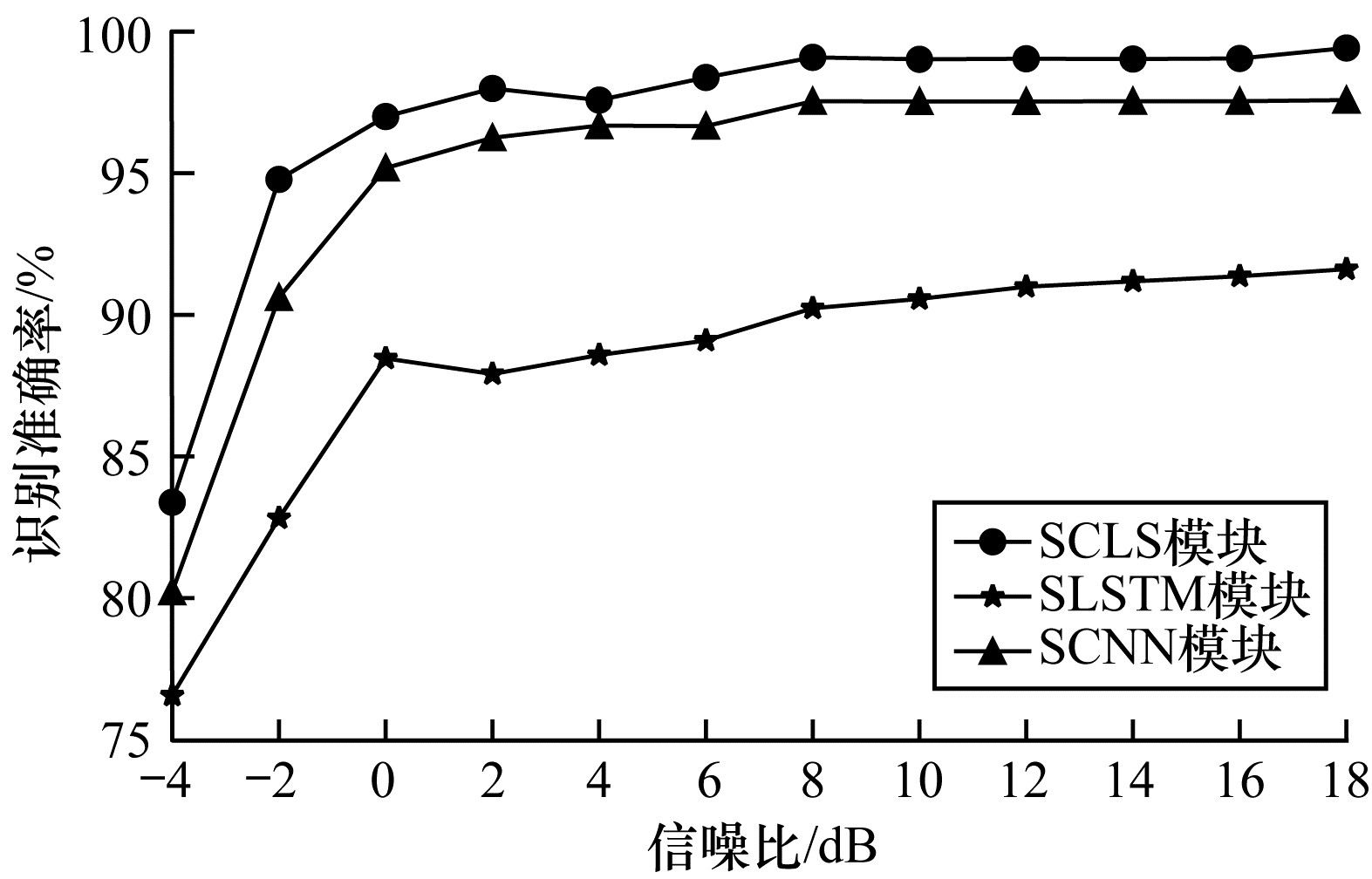
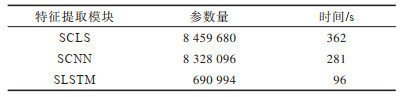
在每类调制信号的样本数量为720的条件下,将基于本文SCLS网络结构的特征提取模块(简称SCLS模块)与基于SCNN网络结构的特征提取模块(简称SCNN模块)和基于SLSTM网络结构的特征提取模块(简称SLSTM模块)进行对比分析,其中,SCNN网络结构为文献[2]中原CNN网络结构与孪生网络相结合的网络结构,SLSTM网络结构为文献[22]中原LSTM网络结构与孪生网络结构相结合的网络结构。3种特征提取模块对10种调制信号的识别准确率如图 6所示。可以看出,在孪生网络结构下基于CNN与LSTM的特征提取模块识别性能最好,其次是基于CNN的特征提取模块,基于LSTM的特征提取模块识别性能最差。当SNR为-4 dB时,SCLS、SCNN和SLSTM特征提取模块的识别准确率分别为82%、79%和75%;随着SNR的增大,SCLS、SCNN和SLSTM特征提取模块的识别准确率分别稳定在98%、96%和90%。在整个测试集中3种特征提取模块的平均识别准确率如表 1所示,其算法实现所需的训练参数与训练时间如表 2所示。由表 1可以看出,SCLS特征提取模块对调制信号的平均识别率最高,比SCNN和SLSTM特征提取模块高2.24和9.04个百分点,这是由于不同调制信号具有不同的空间特征和时序特征,串联的CNN和LSTM可同时提取空间特征和时序特征。由表 2可以看出,SCLS特征提取模块相较其他两种特征提取模块训练参数更多,训练时间更长,算法复杂度更高,这是该模块需要改进之处。
|
Download:
|
| 图 6 3种特征提取模块的识别性能比较 Fig. 6 Comparison of recognition performance of three feature extraction modules | |

|
下载CSV 表 1 3种特征提取模块的平均识别准确率比较 Table 1 Comparison of average recognition accuracy of three feature extraction modules |
|
下载CSV 表 2 3种特征提取模块所需训练参数量与时间比较 Table 2 Comparison of the amount of training parameters and time required for three feature extraction modules |
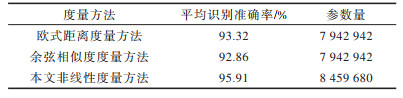
为验证网络相似度度量方法对算法性能的影响,将本文非线性相似度度量方法与欧氏距离和余弦相似度度量方法进行对比分析,结果如表 3所示。由表 3可以看出,与固定的欧式距离度量和余弦相似度度量方法相比,本文非线性相似度度量方法的识别准确率分别提升2.59和3.05个百分点,但是算法复杂度也相应有所增加,其主要原因为本文通过神经网络进行相似度度量,度量网络可与特征提取网络联合训练,所提取的样本特征同时满足度量网络的约束,而固定的欧式距离度量和余弦相似度度量方法则较依赖特征提取模块所提取的特征。
|
下载CSV 表 3 3种度量方法的识别性能对比 Table 3 Comparison of the recognition performance of three measurement methods |
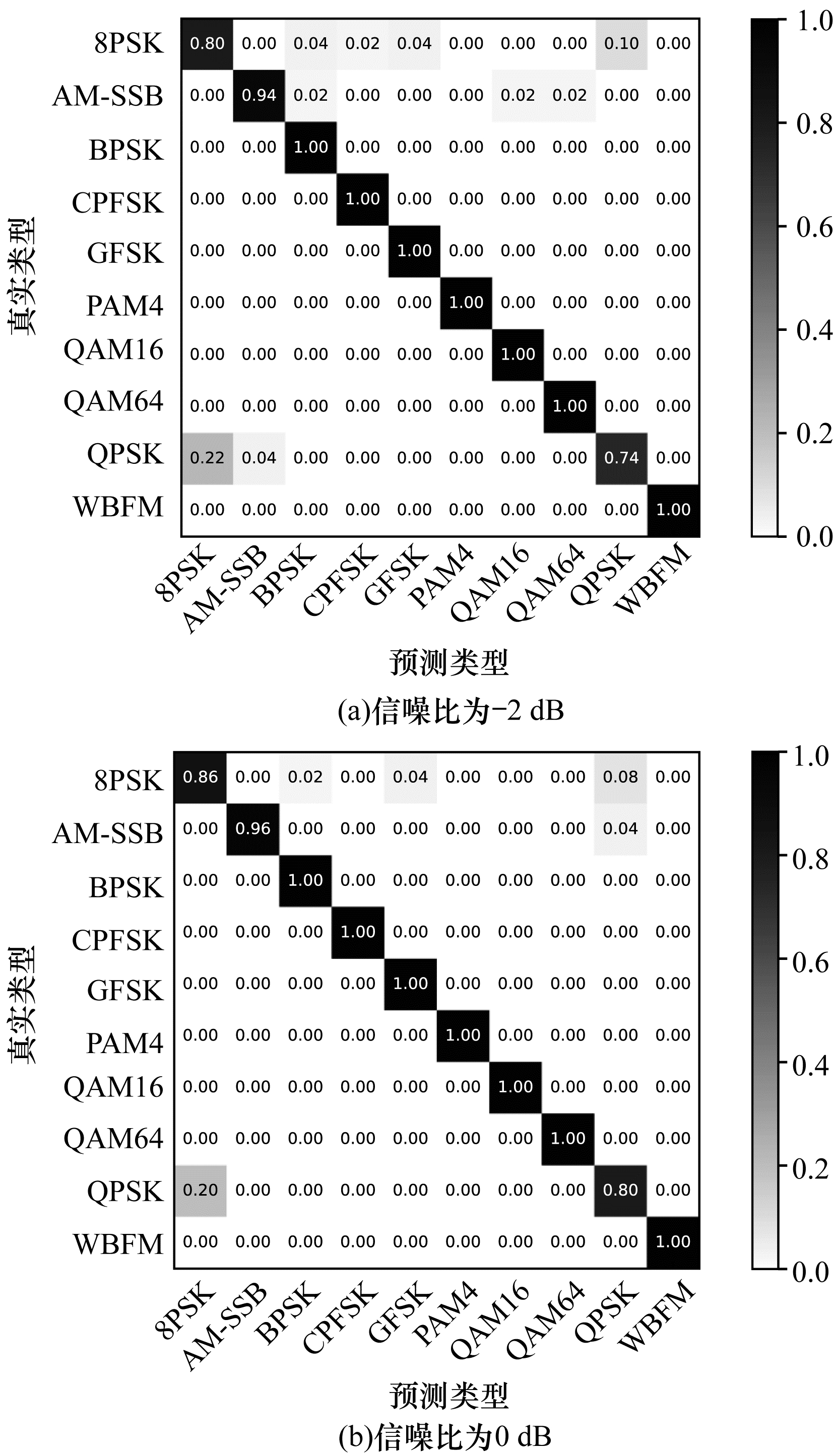
在每类调制信号的样本数量为720的条件下,将随机制作与优先制作类别相近的训练样本标签在低信噪比条件下进行识别性能对比,结果如图 7、图 8所示。可以看出,本文算法在低信噪比时仍具有较好的识别性能,但是其对于8PSK和QPSK的识别容易混淆,主要原因为这两种调制样式在IQ时序图表示上相似性较大,在低信噪比的噪声影响下使得两者更加难以区分,并且在训练过程中由于随机制作标签的影响导致这两种调制方式的类间组合相对较少,提取的特征不能较好地区分这两种调制方式。
|
Download:
|
| 图 7 随机标签在信噪比为-2 dB和0 dB时的混淆矩阵 Fig. 7 Confusion matrix of random label when SNR is -2 dB and 0 dB | |
|
Download:
|
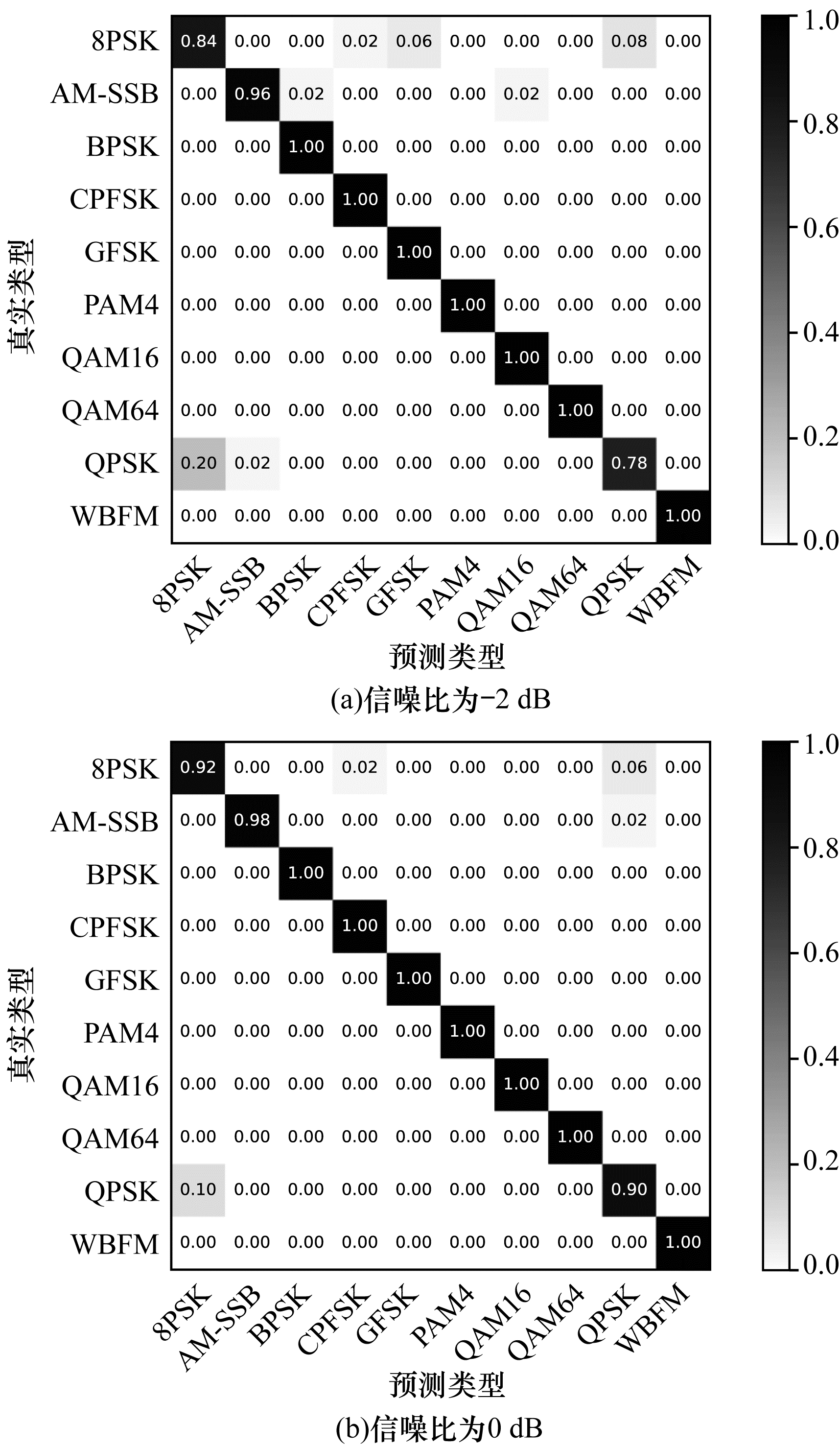
| 图 8 优先标签在信噪比为-2 dB和0 dB时的混淆矩阵 Fig. 8 Confusion matrix of priority label when SNR is -2 dB and 0 dB | |
通过对较相似的调制方式进行优先制作相似类间标签可在训练过程中提取出更好区分两者的特征向量,并且在低信噪比条件下相较随机制作标签具有更好的识别性能。基于以上实验的对比与分析得出,本文算法相比传统基于深度学习的调制识别算法在训练过程中可有效降低所需样本量,并且本文采用的级联特征提取模块与距离度量模块可进一步提升算法的识别性能。
4 结束语本文结合通信信号时序图的时空特性,提出一种基于深度孪生网络的小样本调制识别算法,利用由CNN和LSTM级联的特征提取模块提取特征,并在孪生网络架构上通过距离度量模块对提取特征进行相似度度量,实现小样本条件下的调制识别。实验结果表明,该算法在训练过程中所需样本量明显减少,并且相较单一特征提取网络识别准确率更高。后续将通过半监督学习技术对大量无标签的训练样本进行网络预训练,进一步降低网络训练过程中所需的样本量并提高算法运行速度。
| [1] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E.ImageNet classification with deep convolutional neural networks[C]//Proceedings of the 26th Annual Conference on Neural Information Processing Systems.New York, USA:ACM Press, 2012:1106-1114.
|
| [2] |
O'SHEA T J, CORGAN J, CLANCY T C.Convolutional radio modulation recognition networks[C]//Proceedings of International Conference on Engineering Applications of Neural Networks.Berlin, Germany:Springer, 2016:213-226.
|
| [3] |
BAI Pengyuan, XU Hua, SUN Li. A recognition algorithm for modulation schemes by convolution neural network and spectrum texture[J]. Journal of Northwestern Polytechnical University, 2019, 37(4): 816-823. (in Chinese) 白芃远, 许华, 孙莉. 基于卷积神经网络与时频图纹理信息的信号调制方式分类方法[J]. 西北工业大学学报, 2019, 37(4): 816-823. |
| [4] |
ZHANG Zufan, WANG Chun, GAN Chenquan, et al. Automatic modulation classification using convolutional neural network with features fusion of SPWVD and BJD[J]. IEEE Transactions on Signal and Information Processing over Networks, 2019, 5(3): 469-478. DOI:10.1109/TSIPN.2019.2900201 |
| [5] |
LI F F, FERGUS R, PERONA P. One-shot learning of object categories[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(4): 594-611. DOI:10.1109/TPAMI.2006.79 |
| [6] |
MEHROTRA A, DUKKIPATI A.Generative adversarial residual pairwise networks for one shot learning[EB/OL].[2020-04-03].https://arxiv.org/abs/1703.08033.
|
| [7] |
DIXIT M, KWITT R, NIETHAMMER M, et al.AGA:attribute guided augmentation[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C., USA:IEEE Press, 2017:7455-7463.
|
| [8] |
HARIHARAN B.Low-shot visual recognition by shrinking and hallucinating features[C]//Proceedings of 2017 IEEE International Conference on Computer Vision.Washington D.C., USA:IEEE Press, 2017:3037-3046.
|
| [9] |
FINN C.Model-agnostic meta-learning for fast adaptation of deep networks[C]//Proceedings of the 34th International Conference on Machine Learning.New York, USA:ACM Press, 2017:1126-1135.
|
| [10] |
SANTORO A.Meta-learning with memory-augmented neural networks[C]//Proceedings of the 33rd International Conference on Machine Learning.New York, USA:ACM Press, 2016:1842-1850.
|
| [11] |
RAVI S, LAROCHELLE H.Optimization as a model for few-shot learning[EB/OL].[2020-04-03].https://blog.csdn.net/weixin_37589575/article/details/96995985.
|
| [12] |
KOCH G, ZEMEL R, SALAKHUTDINOV R.Siamese neural networks for one-shot image recognition[EB/OL].[2020-04-03].http://www.cs.utoronto.ca/~gkoch/files/msc-thesis.
|
| [13] |
VINYALS O.Matching networks for one shot learning[C]//Proceedings of the 30th Conference on Neural Information Processing Systems.Washington D.C., USA:IEEE Press, 2016:3630-3638.
|
| [14] |
SNELL J.Prototypical networks for few-shot learning[C]//Proceedings of the 31st Conference on Neural Information Processing Systems.Washington D.C., USA:IEEE Press, 2017:4080-4090.
|
| [15] |
SUNG F.Learning to compare:relation network for few-shot learning[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition.Washington D.C., USA:IEEE Press, 2018:1199-1208.
|
| [16] |
WANG Peng.Multi-attention network for one shot learning[C]//Proceedings of 2017 IEEE Conference on Computer Vision and Pattern Recognition.Washington D.C., USA:IEEE Press, 2017:6212-6220.
|
| [17] |
HILLIARD N, HODAS N O, CORLEY C D.Dynamic input structure and network assembly for few-shot learning[EB/OL].[2020-04-03].https://arxiv.org/abs/1708.06819v1.
|
| [18] |
BROMLEY J, GUYON I, LECUN Y, et al. Signature verification using a Siamese time delay neural network[J]. International Journal of Pattern Recognition and Artificial Intelligence, 1993, 7(4): 669-688. DOI:10.1142/S0218001493000339 |
| [19] |
O'SHEA T J, WEST N.Radio machine learning dataset generation with GNU radio[C]//Proceedings of GNU Radio Conference.Washington D.C., USA:IEEE Press, 2016:1-7.
|
| [20] |
KINGMA D P, BA J.Adam:a method for stochastic optimization[EB/OL].[2020-04-03].https://www.oalib.com/paper/4068193.
|
| [21] |
BISHOP C M. Pattern recognition and machine learning(information science and statistics)[M]. Berlin, Germany: Springer, 2006.
|
| [22] |
ZHOU Jiang.Research and implementation of communication signal modulation recognition based on neural network[D].Chengdu:University of Electronic Science and Technology, 2018.(in Chinese) 周江.基于神经网络的通信信号调制识别研究及实现[D].成都:电子科技大学, 2018. |
 2021, Vol. 47
2021, Vol. 47
