近年来,深度学习方法在图像分类[1-3]、目标检测[4-6]等计算机视觉领域具有广泛应用,而应用的重要前提是使用海量带标注样本对深度学习模型加以训练。在很多特殊的应用场景下,获取大量标注样本成本较高,因此,如何赋予模型在少量样本中具有快速学习的能力并识别新的实体成为亟待解决的问题。
人类视觉模型从少量新事物中快速抽象出具有代表性概念的能力优于深度学习模型的学习过程。对于一类新事物,人类往往仅需要通过观察便可完成学习过程,并能够对新实体进行准确判断。为赋予深度学习模型快速学习的能力,小样本学习[7-9]问题应运而生。其中新实体称为查询样本,已观察的样本称为支持样本。
小样本学习问题是一类特殊的图像分类问题,此类任务要求使用少量待测试类别的训练样本构建性能优良的分类模型,而人类视觉模型的快速学习能力可满足小样本学习任务的需求。考虑人类认识并识别一类新事物的过程,首先需观察一个或数个新事物的实体,并从中抽象出具有代表性的特征,而在遇到新的实体时,则通过对比新实体特征与脑海中各类事物特征的相近程度完成对新实体类别的判断。受此启发,小样本学习的计算机视觉模型通常建模一个用于判断样本间相似度的分类器,该类方法称为度量学习。
度量学习处理过程符合人类在解决小样本问题时的思维方式,基于这一学习方式,研究人员提出了众多具有代表性的小样本学习方法。文献[10]提出孪生网络,通过多层神经网络提取查询样本及支持样本的深层卷积特征,并以二分类网络判断两个样本是否为同一类别。该方法仅计算样本视觉特征间距离,未利用同类别样本间的共同语义信息,如对不同种类的鸟进行分类时,仅利用鸟的视觉特征进行分类是不充分的,因为鸟总体的外形是非常相似的,依靠视觉特征进行分类的方法很可能会将鸟分到错误的类别中。而网络如果可以在图像视觉特征的基础上,进一步利用样本的语义信息,即视觉特征相似的物体属于不同的类别,则可以更加准确地对物体进行分类。文献[11]提出原型网络,该方法首先学习同类支持样本之间的原型(Prototype)表示,然后判断查询样本与支持样本间的原型距离以分类该样本所属的类别,其本质上仍是通过距离度量进行样本识别。文献[12]提出关系网络,通过建模一个小型网络来计算支持集和查询集的样本特征,使用另一个简单的网络判断特征间的距离。文献[13]提出匹配网络,首先提取目标视觉特征,然后以余弦距离表征目标间的相似性。上述方法总体思想均为视觉特征的距离度量,该类方法由于仅考虑视觉相关性,缺失语义显著性特征,在背景干扰等复杂场景下存在明显弊端。
本文提出语义匹配网络的小样本学习方法,提取支持样本的多尺度深层卷积特征,通过双注意力模型匹配样本间的语义信息,使得同类间各尺度特征相近,不同类之间的各尺度特征远离,使网络可以通过学习目标类别间的可区分语义特征提升分类效果。该方法通过多层级特征匹配提取,可缓解ResNet[14]网络结构在小样本学习中的过拟合问题。
1 本文方法本节阐述小样本学习的问题定义,并介绍本文的语义匹配网络方法,该方法主要由特征提取网络、特征语义匹配网络及特征分类网络三部分组成。本文方法的整体流程如图 1所示,其中,EM(Embedding Moudle)为特征提取模块,SM(Semantic Moudle)为语义匹配模块。给定一组支持集图片和一张查询样本,通过HeadNet降维图像输入,根据特征提取模块提取图像的多尺度特征,通过各尺度的语义匹配网络提取语义依赖关系,其中各尺度特征和语义匹配模块均接收其上层模块特征用以特征融合。最后根据分类特征分类网络获取各尺度下的查询样本与所有支持样本的相似度,并加权得到最终分类结果,查询样本的类别与支持样本的相似度呈正相关。
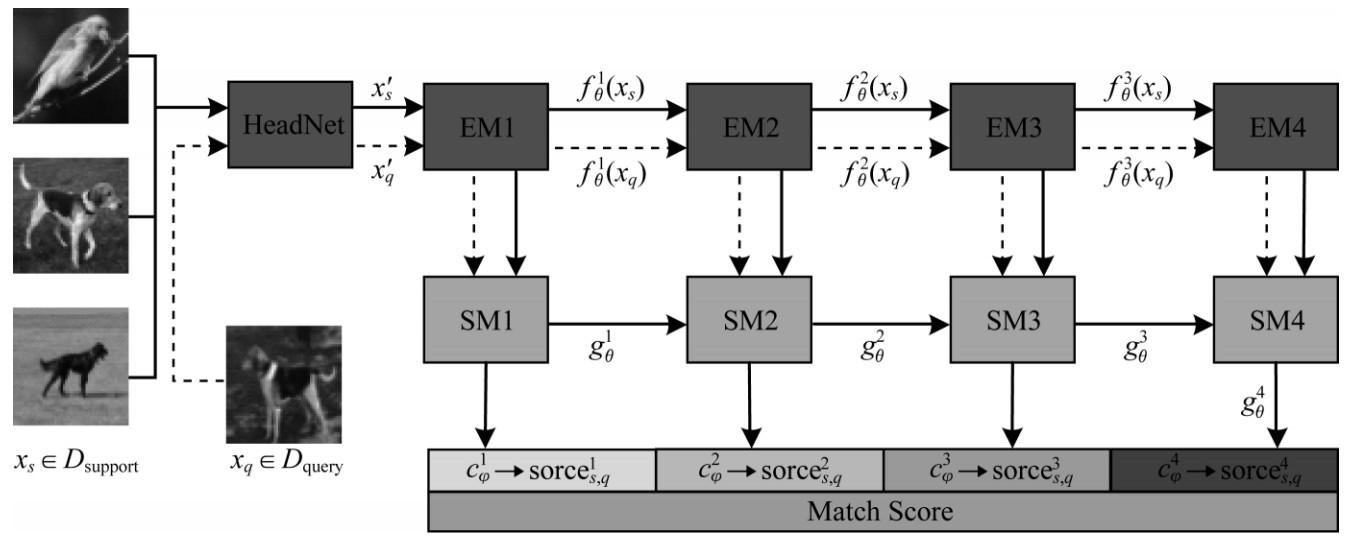
|
Download:
|
| 图 1 语义匹配网络的整体结构 Fig. 1 Overall structure of semantic matching network | |
区别于经典分类问题,小样本学习方法将训练集分为支持集
| $ {D}_{m\mathrm{-}\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}}=\left\{\left\{{x}_{11}, {x}_{12}, \cdots , {x}_{1k};{y}_{1}\right\}, \cdots \left\{{x}_{i1}, {x}_{i2}, \cdots , {x}_{ik};{y}_{i}\right\}\right\} $ | (1) |
其中
| $ {D}_{m\mathrm{-}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{r}\mathrm{y}}=\left\{\left\{{\stackrel{-}{x}}_{11}, {\stackrel{-}{x}}_{12}, \cdots , {\stackrel{-}{x}}_{1k\text{'}};{y}_{1}\right\}, \cdots , \left\{{\stackrel{-}{x}}_{i1}, {\stackrel{-}{x}}_{i2}, \cdots , {\stackrel{-}{x}}_{ik\text{'}};{y}_{i}\right\}\right\} $ | (2) |
其中,
本文网络的整体结构如图 1所示,给定支持样本
| $ {f}_{\theta }^{v}\left({x}_{s}\right)={f}_{\theta }^{v}\left({f}_{\theta }^{v-1}\right({x}_{s}\left)\right)+{f}_{\theta }^{v-1}\left({x}_{s}\right) $ | (3) |
| $ {f}_{\theta }^{v}\left({x}_{q}\right)={f}_{\theta }^{v}\left({f}_{\theta }^{v-1}\right({x}_{q}\left)\right)+{f}_{\theta }^{v-1}\left({x}_{q}\right) $ | (4) |
其中
| $ {g}_{\vartheta }^{v}={g}^{v}\left(\right[{f}_{\theta }^{v}\left({x}_{s}\right)\mathrm{ }, {f}_{\theta }^{v}\left({x}_{q}\right)]+{g}_{\vartheta }^{v-1})) $ | (5) |
其中,
| $ \mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}=\sum \limits_{v=1}^{V}{w}_{v}\cdot \mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}^{v}=\sum\limits_{v=1}^{V}{w}_{v}\cdot {c}_{\phi }^{v}\left({g}_{\vartheta }^{v}\right) $ | (6) |
其中,
视觉识别需要丰富的特征表示,浅层特征包含图像细节纹理而深层特征包含图像抽象语义,本文采用如图 2所示的网络结构来提取特征,通过分别提取不同尺度和深度的卷积特征及特征融合获取图像的表征。该网络主要分为两个部分,即自上而下的编码网络与自下而上的解码网络。在网络结构中,每一层都与同级尺度和上下级尺度连接,由此网络的多尺度特征表示可以更充分有效地提取图像特征。
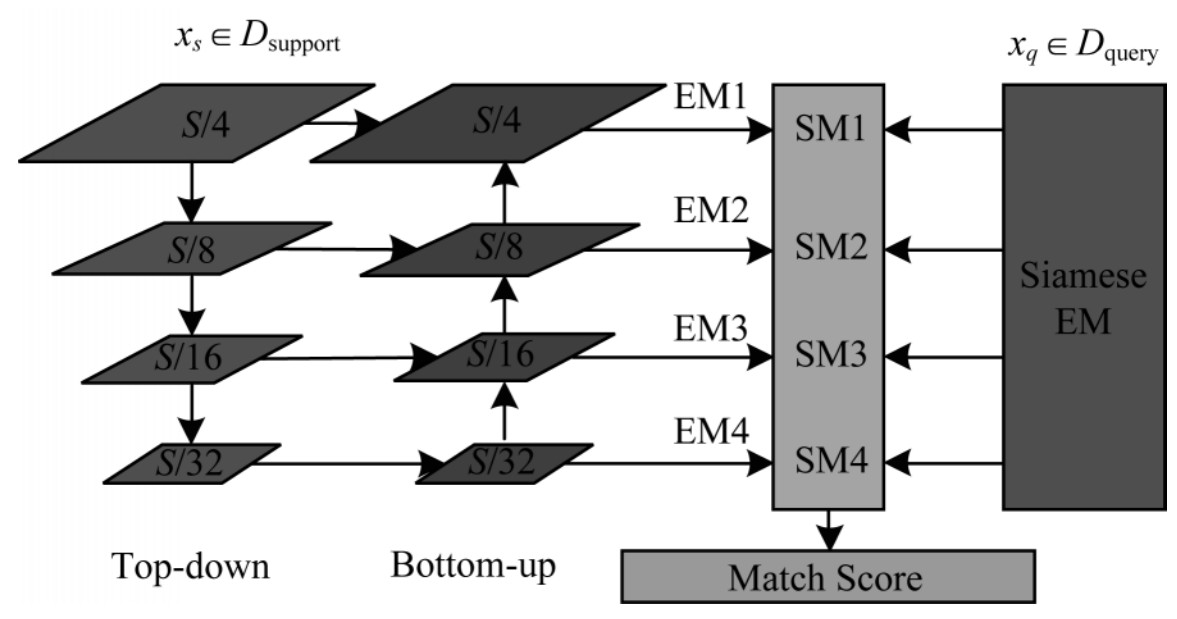
|
Download:
|
| 图 2 特征提取网络结构 Fig. 2 Structure of feature extraction network | |
给定尺度为S×S的图片,经过HeadNet降维后,得到尺度为S/4×S/4的特征,将其输入至特征提取网络可以得到各尺度的输出为:
| $ \mathrm{E}{\mathrm{M}}_{v}\left(x\right)=\phi (T{d}_{v}\left(x\right)+\mu (B{u}_{v}\left(x/2\right)\left)\right) $ | (7) |
其中,
经过特征提取网络后,可得到图像的视觉特征表示,先前基于距离度量的小样本学习方法一般直接将此视觉特征用于后续的距离计算中,并将查询样本归为距离最近的类别。该计算过程仅利用了样本的视觉特征,而忽略了样本间潜在的语义联系。本文在计算视觉特征的距离之前做了语义匹配的操作,进一步提取样本间抽象的语义联系,并利用该语义联系指导特征提取网络的工作,使其更加关注样本间的语义信息而非仅仅是图像的视觉特征,从而使得后续的分类网络可以根据样本间的语义联系更准确地分类。语义匹配的操作如图 3所示,其中
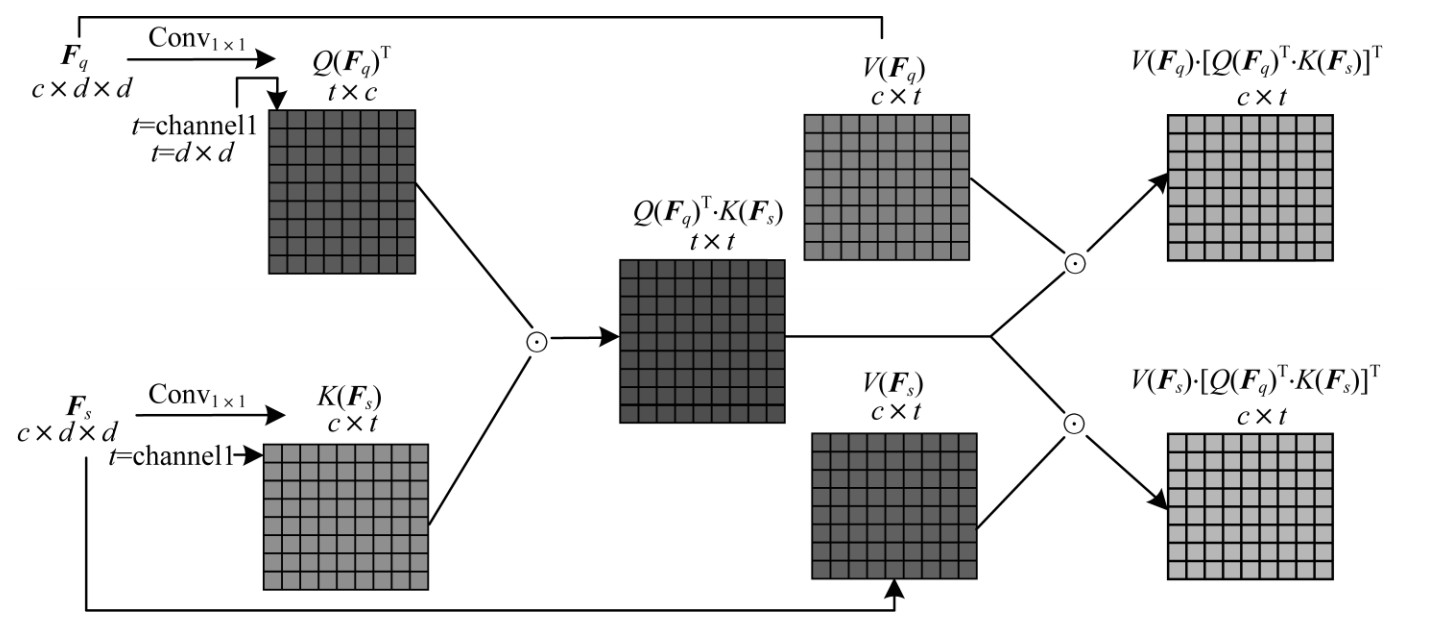
|
Download:
|
| 图 3 dual-attention语义的匹配过程 Fig. 3 Matching process of dual-attention semantics | |
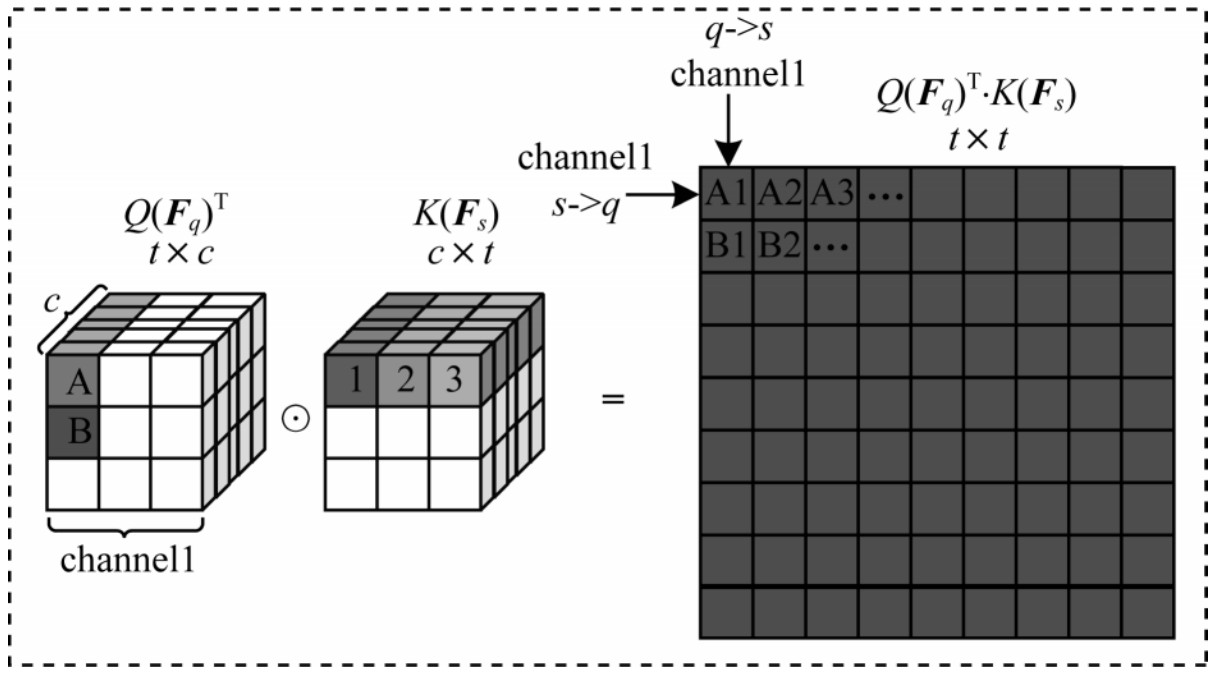
在图 3中,给定支持样本和查询样本的特征尺度为
| $ \boldsymbol{a}\boldsymbol{t}{\boldsymbol{t}}_{sq}=Q\mathrm{C}\mathrm{o}\mathrm{n}{\mathrm{v}}_{1\times 1}({\boldsymbol{F}}_{q}{)}^{\mathrm{T}}\cdot K\mathrm{C}\mathrm{o}\mathrm{n}{\mathrm{v}}_{1\times 1}({\boldsymbol{F}}_{s})\mathrm{ }, \boldsymbol{a}\boldsymbol{t}{\boldsymbol{t}}_{sq}\in {\mathbb{R}}^{{D}^{2}\times {D}^{2}} $ | (8) |
其中,
|
Download:
|
|
图 4 |
|
接着将
| $ \boldsymbol{a}\boldsymbol{t}{\boldsymbol{t}}_{mq}=V\mathrm{C}\mathrm{o}\mathrm{n}{\mathrm{v}}_{1\times 1}\left({\boldsymbol{F}}_{q}\right)\cdot \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{a}\mathrm{t}{\mathrm{t}}_{sq}^{\mathrm{T}}\right)\mathrm{ }, \boldsymbol{a}\boldsymbol{t}{\boldsymbol{t}}_{mq}\in {\mathbb{R}}^{C\times {D}^{2}} $ | (9) |
| $ \boldsymbol{a}\boldsymbol{t}{\boldsymbol{t}}_{ms}=V\mathrm{C}\mathrm{o}\mathrm{n}{\mathrm{v}}_{1\times 1}^{\mathrm{\text{'}}}\left({\boldsymbol{F}}_{s}\right)\cdot \mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}\left(\mathrm{a}\mathrm{t}{\mathrm{t}}_{sq}^{\mathrm{T}}\right)\mathrm{ }, \boldsymbol{a}\boldsymbol{t}{\boldsymbol{t}}_{ms}\in {\mathbb{R}}^{C\times {D}^{2}} $ | (10) |
其中
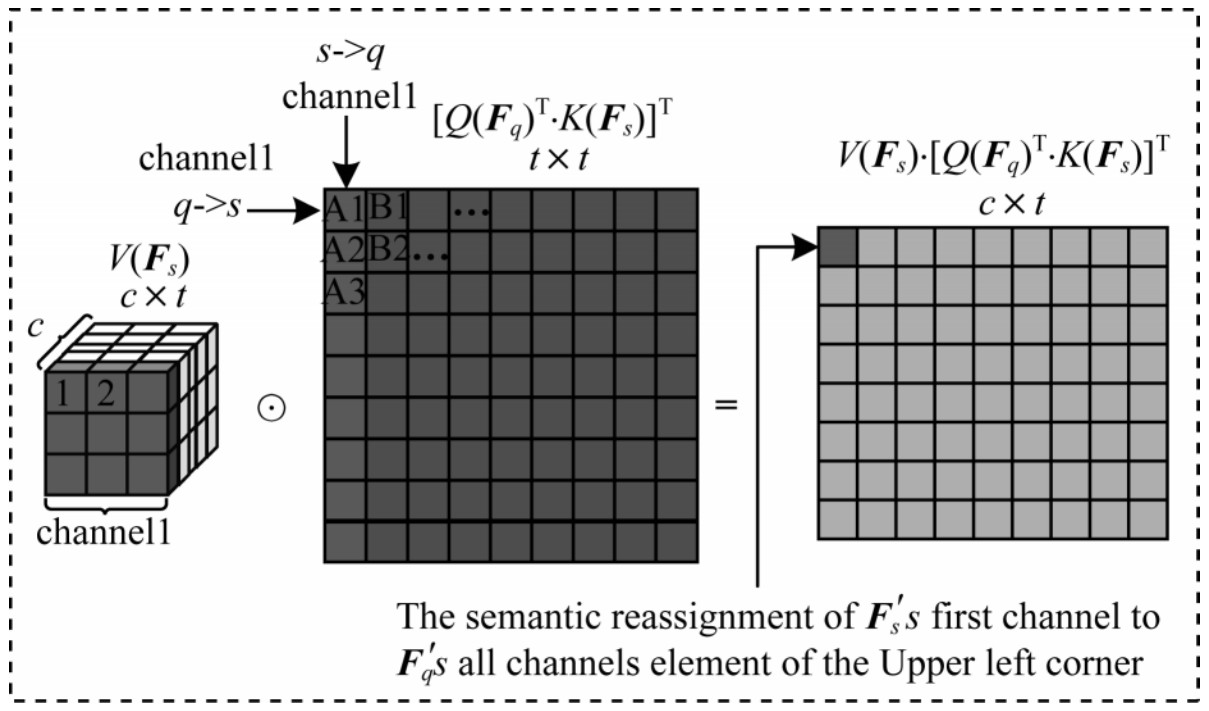
|
Download:
|
|
图 5 |
|
最后经过dual-attention模块匹配和增强语义后的特征为:
| $ \mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}\_\mathrm{a}\mathrm{t}\mathrm{t}\left({\boldsymbol{F}}_{s\cdot q}\right)=\gamma \cdot \boldsymbol{a}\boldsymbol{t}{\boldsymbol{t}}_{ms\cdot q}+{\boldsymbol{F}}_{s\cdot q} $ | (11) |
其中,
图 1中的匹配分数输出为各级尺度下的支持样本和查询样本的匹配分数,该模块主要的作用有两部分:根据不同尺度的输入特征计算该级别下的匹配分数;根据训练和测试的不同,在训练时产生各级别特征尺度下的损失,在测试时对各级别的分数进行加权生成一个查询样本对支持样本的总分数。在训练时各级别的分数如式(12)所示,由于
| $ \mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}^{v}=\mathrm{F}\mathrm{C}\left(\mathrm{A}\mathrm{v}\mathrm{g}\left(\mathrm{d}\mathrm{u}\mathrm{a}\mathrm{l}\_\mathrm{a}\mathrm{t}{\mathrm{t}}^{v}\left({F}_{sq}^{v}\right)\right)\right), \mathrm{ }\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}^{v}\in \left[\mathrm{0, 1}\right] $ | (12) |
| $ \begin{array}{l}\mathrm{b}\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}=-\sum\limits _{v=1}^{V}{w}_{v}\cdot \left[1\right({y}_{s}={y}_{q})\cdot \mathrm{l}\mathrm{o}{\mathrm{g}}_{a}\mathrm{ }\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}^{v}+\\ {\boldsymbol{0}}({y}_{s}={y}_{q})\cdot \mathrm{l}\mathrm{o}{\mathrm{g}}_{a}(1-\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}^{v})]\end{array} $ | (13) |
| $ \mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}=\sum \limits_{v=1}^{V}{w}_{v}\cdot \mathrm{s}\mathrm{o}\mathrm{r}\mathrm{c}{\mathrm{e}}_{s, q}^{v} $ | (14) |
其中
本节主要通过在小样本学习数据集Omniglot和miniImageNet上对比本文方法与其他主流方法,如匹配网络(Matching Net)、原型网络(Prototypical Net)、相关网络(Relation Net)、元学习LSTM(Meta LSTM)[16]、未知模型元学习(MAML)[17]、图网络(Graph Neural Net)[18]、DynamicFSL[19]、AdaResNet[20]和PPA[21]等,并详细验证本文方法Bottom-up模块和dual-att语义匹配模块对最终结果的影响。
本文通过Adam[22]算法优化整个模型,初始学习率为0.001,1 000个episodes为一代,每10代将学习率降为原来的一半,训练过程共有100代。整个模型从零开始训练,在训练前使用xavier[23]方法进行权重的初始化配置。在训练和测试中,使用标准的数据增强方法,如随机将图片裁剪为固定尺度、随机的水平翻转以及图片像素值的归一化操作等。
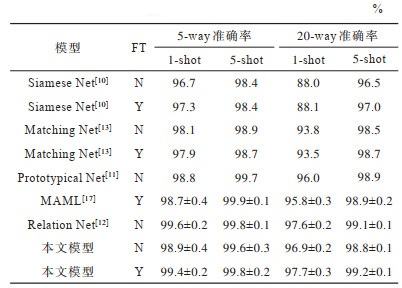
2.1 在Omniglot数据集上的实验Omniglot数据集由50个字母共计1 623类字符组成,每类字母均为20个样本,由不同人手写而成。该数据集是小样本学习领域早期常用的数据集,本文采用和匹配网络一样的数据集设置:将样本大小统一变为28×28,并且使用旋转90°的样本增强方法。使用1 200类用于训练,423类用于测试。由于数据集样本尺度问题,本文提出的网络结构需要稍微修改,将HeadNet的输入通道、步长和padding变为1,以适应图片的输入,为了防止过拟合,将HeadNet和EM的卷积层数变为1,实验结果如表 1所示,其中,FT表示微调。
|
下载CSV 表 1 Omniglot数据集上的小样本分类准确率 Table 1 Few-shot classification accuracy on Omniglot dataset |
从表 1可以看出,500次结果的平均值在95% 置信区间的取值,本文的效果较匹配网络和原型网络都有较大提升,在大部分任务上取得了目前已知的最好效果。实验结果表明,本文语义匹配网络能够较好地提升小样本学习方法的分类准确率。
2.2 在miniImageNet数据集上的实验miniImageNet数据集是在ImageNet数据集基础上选出的,分为100个类别,每个类别挑选600个样本,共计由60 000张样本组成。其中,64类用于训练,16类用于验证,20类用于测试。本文在训练时采用常用的episode中每个类别包含5个查询样本的设置,这样对于5-way-1-shot任务共有5×5+1×5=30张样本参与训练,5-way-5-shot任务共有5×5+5×5=50张样本参与训练。在测试时由于显存不同于其他小样本学习方法常用的每类包含15个查询样本的设置,本文采用的每类10张查询样本用于测试实验效果,并且使用5次实验结果平均值作为最终结果的方法确保实验结果的准确性。
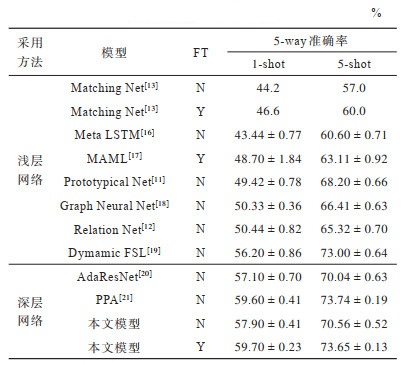
在miniImageNet数据集上的小样本分类准确率实验结果如表 2所示。
|
下载CSV 表 2 miniImageNet数据集上的小样本分类准确率 Table 2 Few-shot classification accuracy on miniImageNet dataset |
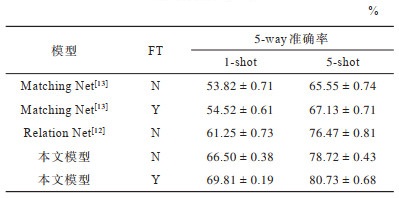
从表 2可以看出,相较于采用浅层网络的传统特征提取和分类方法的模型,本文模型利用特征提取阶段时的语义依赖关系,在数据集上可以提升将近5个百分点。而对于采用深层网络的模型,本文的方法在微调之后依旧有着比较优秀的结果。
为了验证本文方法各个模块对实验结果的影响,本文进行多组对比实验查看各个模块在实验时的表现。表 3为不同模块对实验结果的影响,其中,训练和测试使用的实验配置与5-way-1-shot的相同,√表示使用该模块。

|
下载CSV 表 3 不同模块对实验结果的影响 Table 3 Affect of different modules on experimental results |
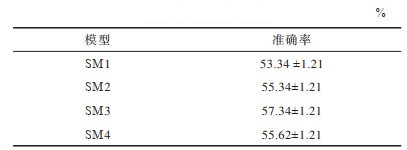
从表 3可以看出,相较于Bottom-up模块,dual-att模块对效果的提升更为显著,表明了样本对之间的语义匹配的重要性,当然结合语义提取的Bottom-up模块,模型可以更好地学习到样本间的语义依赖关系。表 4为不同阶段的输出在数据集上的结果,其实验配置都与5-way-1-shot的相同。
|
下载CSV 表 4 不同阶段输出对实验结果的影响 Table 4 Affect of different stages output on experimental results |
从表 4可以看出,模型的后面阶段特征比较抽象并且更加具有区分性,但是SM4的输出效果没有SM3阶段的效果好,这可能是到SM4阶段时语义匹配产生的输出对分类模块来说尺度较小,不能很好地表达特征差异性的关系,这也是本文在分类模型赋予不同阶段产生的分数对最终查询样本分数权重超参数设置的一个侧面依据。
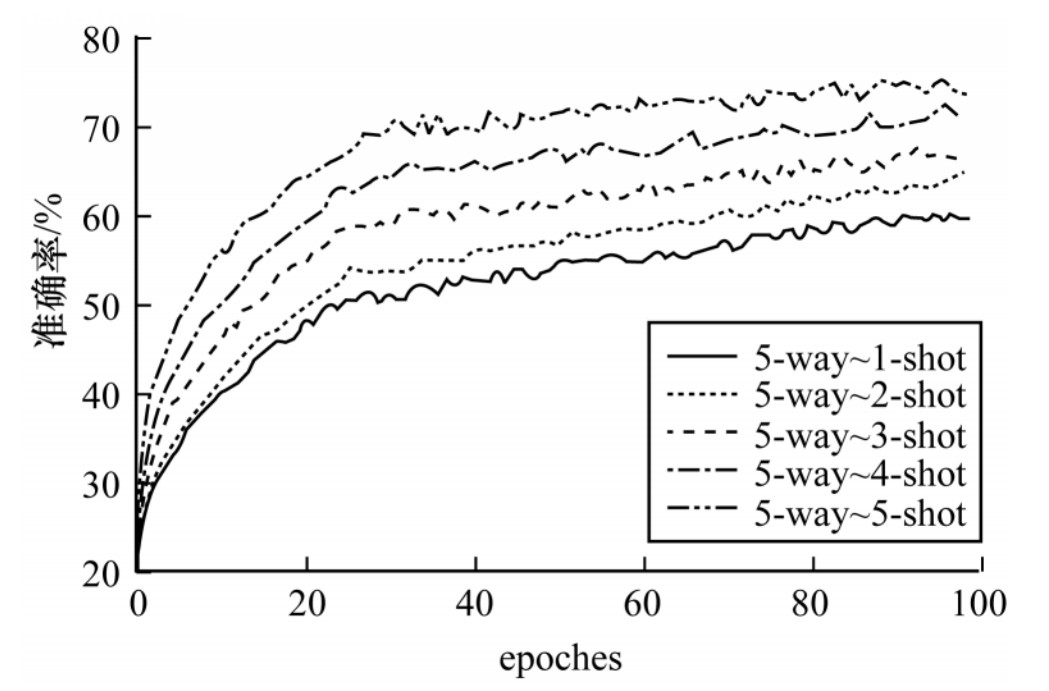
为充分验证本文方法与样本数量的关系,本文分别在5way中1-shot~5-shot的条件下做了对比实验,如图 6所示,可以看出,1-shot~5-shot的测试准确率逐步增加,符合实验预期。
|
Download:
|
| 图 6 5-way-1-shot~5-shot的性能对比结果 Fig. 6 Performance comparison results of 5 -way-1-shot~5-shot | |
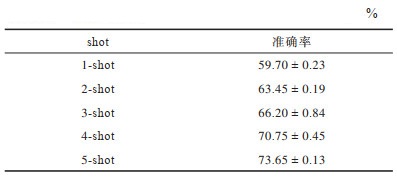
表 5为对比实验的具体数值,其中每增加一个shot的样本数,对测试的准确率都有所提升。并且与一般的分类算法相比,本文算法不需要很多的训练样本数,仅在5个样本数的条件下即可达到73.65%的准确率。而传统的分类算法往往需要成千上百的样本数,如ResNet和DenseNet等算法,在样本数低于10个以下时则不能工作。因此,本文算法仅在少量样本数下即可较好地工作。
|
下载CSV 表 5 5-way-1-shot~5-shot的实验结果 Table 5 Experimental results of 5-way-1-shot~5-shot |
Cifar100数据集有100个类,每个类包含600个样本,分为500个训练样本和100个测试样本,其中100个类被分成20个大类。每个样本都带有一个fine标签(所属的子类)和一个coarse标签(所属的大类)。本文重新组织该数据集,从每个大类中随机挑一个类组成20个类作为测试集,同样不重复地从大类中再各挑一个类组成20个类作为测试集,剩下的60类作为训练集。
与miniImageNet实验相同,本文取5次实验结果平均值作为最终的测试结果,如表 6所示。由表 6可知,相较于匹配网络和关系网络,在5-way-1-shot任务上,本文准确率提高了4个百分点,在5-way-1-shot任务上,本文准确率提高了8个百分点。至此,本文分别在Omniglot、miniImageNet和Cifar100数据集上验证了本文方法的效果,可见本文方法具有一定的泛化能力。
|
下载CSV 表 6 在Cifar100数据集上的小样本分类准确率 Table 6 Few-shot sample classification accuracy on Cifar100 dataset |
本文根据文献[24]中的理论形成注意力热图,可视化查询样本对支持样本各语义依赖层级的输出在原始样本上激活部分。图 7为SM模块在不同层级提取语义聚焦的部分,其中查询样本的类别为狮子,与图中第一个支持样本相同。

|
Download:
|
| 图 7 各语义依赖层级在原始样本上激活部分 Fig. 7 Each semantic dependency level activates parts on the original sample | |
从图 7可以看出,查询样本对与其具有相同类别的样本可以学习到很好的语义信息,其他支持样本的语义信息查询样本则学习很差,查询样本在第二和第三支持样本学到的语义信息大多集中在草地部分,在第四支持样本学到的语义前两层集中在草地,后两层并没有很好地集中在目标物体狮子附近。因为第五支持样本与查询样本比较相似,SM模块可以部分地学到其语义信息,但是对比第一支持样本的语义信息分布,其语义信息并没有第一支持样本语义信息全面。对比SM1~SM4之间各层级的语义信息输出,可以看出,后面层级提取的信息更加抽象和更具有区分性,更好地贴合了目标物体区域。
3 结束语本文针对小样本学习问题提出一种语义匹配网络模型。该模型通过语义提取和匹配操作在样本特征的多尺度语义上提炼出样本之间潜在的语义区别与联系,从而提升后续分类网络的准确率。实验结果表明,本文方法可以有效地归纳出样本之间相似的语义信息,并利用该语义提升网络的性能。样本间的语义联系和注意力机制常见于图像分类和文本理解任务中,但在小样本领域中却未得到足够重视。语义关联和注意力机制能够强化图像表征,在样本量较少的情况下该类特征显得尤为重要,因此下一步将继续研究语义模型和注意力方法在小样本问题中的应用。
| [1] |
KRIZHEVSKY A, SUTSKEVER I, HINTON G E. ImageNet classification with deep convolutional neural networks[C]//Proceedings of NIPS'12. New York, USA: ACM Press, 2012: 84-90.
|
| [2] |
SZEGEDY C, LIU W, JIA Y, et al. Going deeper with convolutions[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1409.4842.
|
| [3] |
HUANG G, LIU Z, VAN DER M L, et al. Densely connected convolutional networks[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1608.06993.
|
| [4] |
REN S, HE K, GIRSHICK R B, et al. Faster R-CNN: towards real-time object detection with region proposal networks[C]//Proceedings of the 28th International Conference on Neural Information Processing Systems. Washington D.C., USA: IEEE Press, 2015: 91-99.
|
| [5] |
REDMON J, DIVVALA S, GIRSHICK R, et al. You only look once: unified, real-time object detection[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2016: 779-788.
|
| [6] |
LIU W, ANGUEIOV D, ERHAN D, et al. SSD: single shot multibox detector[C]//Proceedings of European Conference on Computer Vision. Berlin, Germany: Springer, 2016: 21-37.
|
| [7] |
ZHANG X T, QIANG Y T, SUNG F, et al. RelationNet2: deep comparison columns for few-shot learning[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1811.07100.
|
| [8] |
LI F F, FERGUS L, PERONA R. One-shot learning of object categories[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(4): 594-611. |
| [9] |
LAKE B M, SALAKHUTDINOV R, GROSS J, et al. One shot learning of simple visual concepts[C]//Proceedings of Annual Meeting of the Cognitive Science Society. Boston, USA: [s. n. ], 2011: 1-6.
|
| [10] |
KOCH G, ZEMEL R, SALAKHUTDINOV R. Siamese neural networks for one-shot image recognition[EB/OL]. [2019-11-10]. https://www.cs.cmu.edu/~rsalakhu/papers/oneshot1.pdf.
|
| [11] |
SNELL J, SWERSKY K, ZEMEL R S. Prototypical networks for few-shot learning[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1703.05175.
|
| [12] |
SUNG F, YANG Y, ZHANG W, et al. Learning to compare: relation network for few-shot learning[C]//Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2018: 1199-1208.
|
| [13] |
VINYALS O, BLUNDELL C, LILLICRAP T, et al. Matching networks for one shot learning[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1606.04080.
|
| [14] |
HE Kaiming, ZHANG Xiangyu, REN Shaoqing, et al. Deep residual learning for image recognition[C]//Proceedings of IEEE Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2016: 770-778.
|
| [15] |
VASWANI A, SHAZEER N, PARMAR N, et al. Attention is all you need[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1706.03762.
|
| [16] |
RAVI S, LAROCHELLE H. Optimization as a model for few-shot learning[C]//Proceedings of IEEE International Conference on Learning Representations. Washington D.C., USA: IEEE Press, 2017: 157-168.
|
| [17] |
FINN C, ABBEEL P, LEVINE S. Model-agnostic meta-learning for fast adaptation of deep networks[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1703.03400.
|
| [18] |
GARCIA V, BRUNA J. Few-shot learning with graph neural networks[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1711.04043v1.
|
| [19] |
GIDARIS S, KOMODAKIS N. Dynamic few-shot visual learning without forgetting[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1804.09458.
|
| [20] |
MUNKHDALIA T, YUAN X, MEHRI S, et al. Rapid adaptation with conditionally shifted neurons[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1712.09926v3.
|
| [21] |
QIAO Siyuan, LIU Chenxi, SHEN Wei, et al. Few-shot image recognition by predicting parameters from activations[C]//Proceedings of 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Washington D.C., USA: IEEE Press, 2018: 7229-7238.
|
| [22] |
HAN Zhidong. Dyna: a method of momentum for stochastic optimization[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1805.04933.
|
| [23] |
SHEN Hao. Towards a mathematical understanding of the difficulty in learning with feedforward neural networks[EB/OL]. [2019-11-10]. https://arxiv.org/abs/1611.05827.
|
| [24] |
SELVARAJU R R, COGSWELL M, DAS A, et al. Grad-CAM: visual explanations from deep networks via gradient-based localization[J]. International Journal of Computer Vision, 2020, 128(2): 336-359. |
 2021, Vol. 47
2021, Vol. 47
