开放科学(资源服务)标志码(OSID):
针对传统网络架构部署周期长、运营成本高、网络结构僵化等问题,欧洲电信标准化协会(European Telecommunications Standards Institute,ETSI)提出了网络功能虚拟化(Network Functions Virtualization,NFV)技术[1]。NFV实现了网络功能与专有硬件之间的解耦,通过虚拟化技术实现网络功能的软件化部署,提高了网络的灵活性和资源的利用率,降低了运营商的资本支出(Capital Expenditure,CPEX)和运营开销(Operation Expenses,OPEX)。然而,NFV资源共享的特点也给网络带来了新的安全风险[2]。传统的被动防御手段面向已知特征的威胁,防御滞后于攻击,在应对NFV带来的新的安全风险时缺乏主动性和对攻击的预测能力。
应对上述攻防不对等的格局,可基于拟态防御思想[3]构建NFV拟态防御架构,利用网络系统环境的动态性和不确定性获得防御功能或属性,其基本原理是:通过为每一个网络功能构建多个功能等价的异构体,为系统引入多样性,同时利用动态调度策略定期或不定期地对线上执行体进行替换,为系统引入动态性与随机性,使得攻击者可利用的攻击面不断变化,从而增加攻击者的攻击难度。此外,利用裁决机制对输出结果进行多模裁决,提高系统可靠性与防御鲁棒性。其中动态调度策略是实现拟态防御的关键技术之一,设计合理的调度策略可以有效提升系统的安全性和异构体的利用率。在现有针对调度策略的相关研究中:文献[4]引入了信誉度与相异度2个指标,提出一种基于信誉度与相异度联合优化的执行体选择算法,在保证执行体之间差异性的同时避免了脆弱程度较低的执行体;文献[5]在考虑系统负载因素的情况下,将调度问题转化为安全与负载的动态双目标优化问题,兼顾了系统的安全性与计算性能;文献[6]提出一种随机种子最小相似度的调度策略,首先随机确定种子执行体,然后根据相似度指标选择整体相似度最小的调度方案,实现了动态性和可靠性之间的平衡;文献[7]提出一种基于优先级和时间片的执行体调度算法,首先从时空维度对执行体的相似性进行定义,然后基于相似性指标进行优先级预排序,最后结合时间片策略进行执行体调度。
上述调度策略虽然在一定程度上改善了拟态防御架构的动态性与随机性,但都是根据执行体自身固有的特点进行调度,没有进一步利用裁决机制对异常执行体的定位感知能力做优化调整。拟态裁决机制可以通过对执行体的输出结果进行对比,发现输出异常的执行体,并利用态势感知技术以及大数据分析对异常执行体的系统信息深入研究,从而得到当前环境下攻击的类型和分布。各异构体由于其组成结构不同,暴露的攻击面不同,对不同攻击的防御能力也不同,因此利用拟态裁决机制的反馈结果对调度策略进行适应性地优化调整,可以提高调度策略的有效性和系统的安全性。
为提升NFV拟态防御架构的安全性和调度策略的有效性,本文利用分析器对裁决器的裁决信息进行分析,得到关于攻击状态的反馈信息,并利用演化博弈理论构建一个多状态动态调度演化博弈模型,将在线执行体的不同组合作为NFV拟态防御架构的不同状态。在此基础上,利用复制动态方程和李雅普诺夫间接法对不同状态下攻防策略的演化趋势和稳定性进行分析,提出基于演化博弈的最优动态调度策略选取算法。
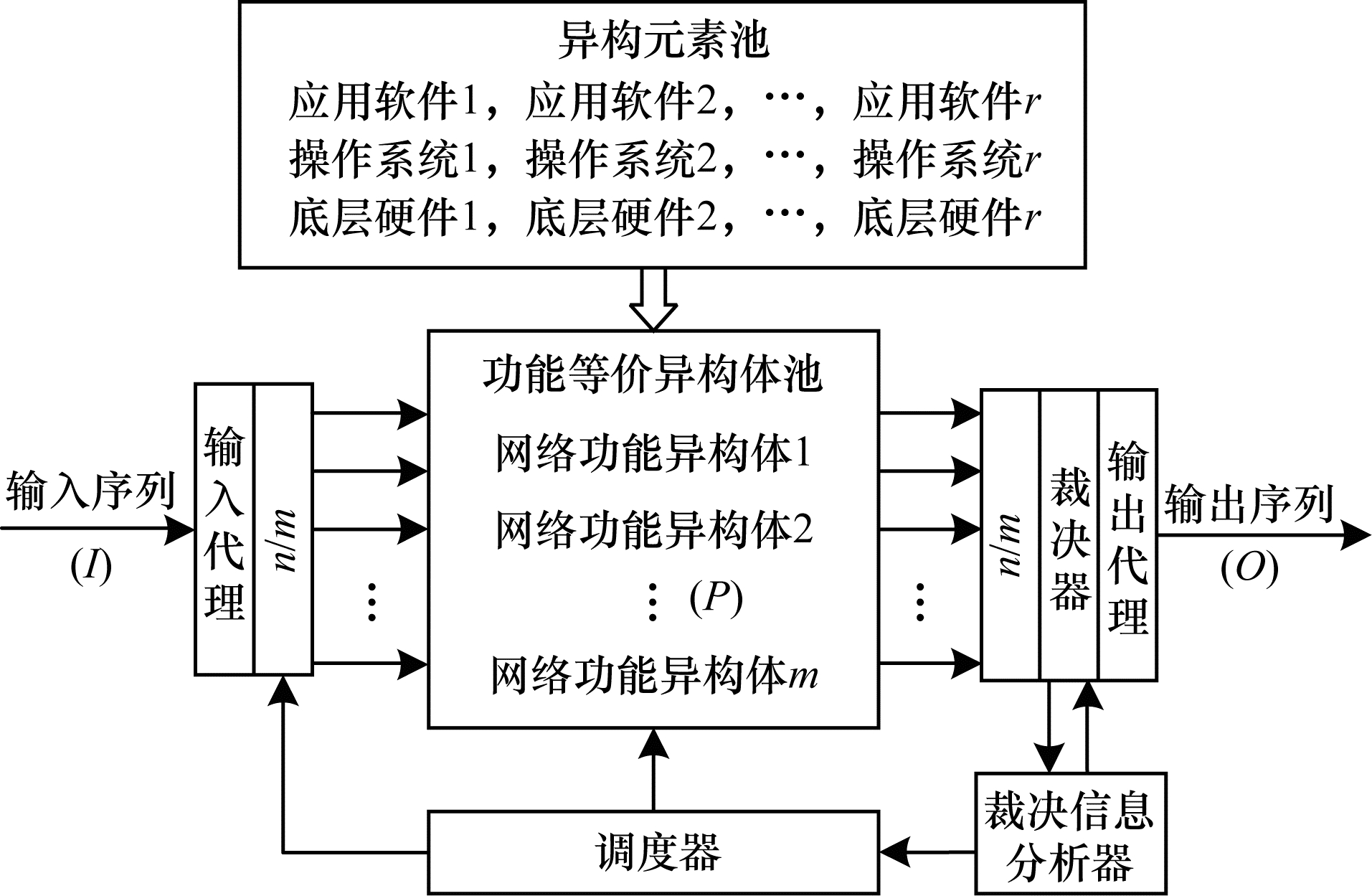
1 NFV拟态防御架构NFV拟态防御架构是一个基于拟态防御理论的内生安全防御体系。图 1为NFV拟态防御架构的示意图,可以看出该架构由异构元素池、异构体池、调度器、输入代理、裁决器、输出代理和分析器组成。
|
Download:
|
| 图 1 NFV拟态防御架构 Fig. 1 NFV mimic defense architecture | |
在NFV拟态防御架构中,每一个网络功能异构体由上而下分为3层:
1)应用软件层:采用不同编程语言或算法实现的虚拟网络功能(Virtual Network Function,VNF),是处理服务请求的逻辑功能。
2)操作系统层:包含不同的操作系统和虚拟化软件,操作系统可以采用Windows、Ubuntu、Centos等,虚拟化软件可以采用OpenStack、XEN等,为应用软件层提供必要的运行环境。
3)底层硬件层:可以使用不同厂家的服务器,如X86和ARM,其作用是搭载整个操作系统。
这些异构体在功能上是等效的,但是具有不同的组成结构,因此降低了共模漏洞的可能性。
演化博弈[9]是把传统博弈理论和生物进化理论结合起来的一种理论,其以有限理性作为理论分析的基础。演化博弈可以对博弈双方长期稳定趋势进行分析,符合实际网络攻防对抗动态演化的现实,能够有效提高利用博弈论分析网络对抗行为的准确性和可信度[10]。本节以演化博弈理论为基础构建多状态动态调度演化博弈模型。与模型相关的前提假设如下:
假设1 NFV拟态防御架构是基于“输入-处理-输出”的IPO(Inputs Process Outputs)模型[3],对于相同的输入,会产生一致的输出。因此,本文仅针对由系统漏洞和后门引发的系统异常或者输出错误,而不考虑DDoS(Distributed Denial of Service)[11]等资源消耗型攻击,这样裁决器才能对输出结果进行比较,以判决执行体是否被攻击。
假设2 系统输出异常可能是由内部故障或者外部攻击导致。本文的研究目标是制定适应性的调度策略防御攻击者的攻击,因此,在导致执行体输出异常的因素中不考虑非攻击因素,如环境等原因导致的系统崩溃。
假设3 由于网络环境复杂多变,攻防双方获得的攻防信息是不完全的。此外,由于分析能力和计算能力有限,攻防双方无法通过一次博弈就能找到最优策略,因此本文假设攻防双方都是有限理性的,具有一定的统计分析能力和事后判断能力,但没有事先的预测能力,需要通过不断学习和调整来找到合适的策略。攻击者可以通过网络扫描和渗透等手段对NFV拟态防御架构进行探测,获取防御者的漏洞和后门信息;NFV拟态防御架构可以通过裁决机制感知异常执行体,并利用分析器得到攻击者的分布和攻击的类型。
基于以上假设,下文给出多状态动态调度演化博弈模型(Multi State Dynamic Scheduling Evolutionary Game Model,MSDSEGM)的相关定义。
定义1 多状态动态调度演化博弈模型可用一个五元组表示:
1)
2)
3)
4)
5)
| $ \left(\begin{array}{cccc}{U}_{\mathrm{A}}^{11}, {U}_{\mathrm{D}}^{11}& {U}_{\mathrm{A}}^{12}, {U}_{\mathrm{D}}^{12}& \cdots & {U}_{\mathrm{A}}^{1n}, {U}_{\mathrm{D}}^{1n}\\ {U}_{\mathrm{A}}^{21}, {U}_{\mathrm{D}}^{21}& {U}_{\mathrm{A}}^{22}, {U}_{\mathrm{D}}^{22}& \cdots & {U}_{\mathrm{A}}^{2n}, {U}_{\mathrm{D}}^{2n}\\ \vdots & \vdots & & \vdots \\ {U}_{\mathrm{A}}^{m1}, {U}_{\mathrm{D}}^{m1}& {U}_{\mathrm{A}}^{m2}, {U}_{\mathrm{D}}^{m2}& \cdots & {U}_{\mathrm{A}}^{mn}, {U}_{\mathrm{D}}^{mn}\end{array}\right) $ | (1) |
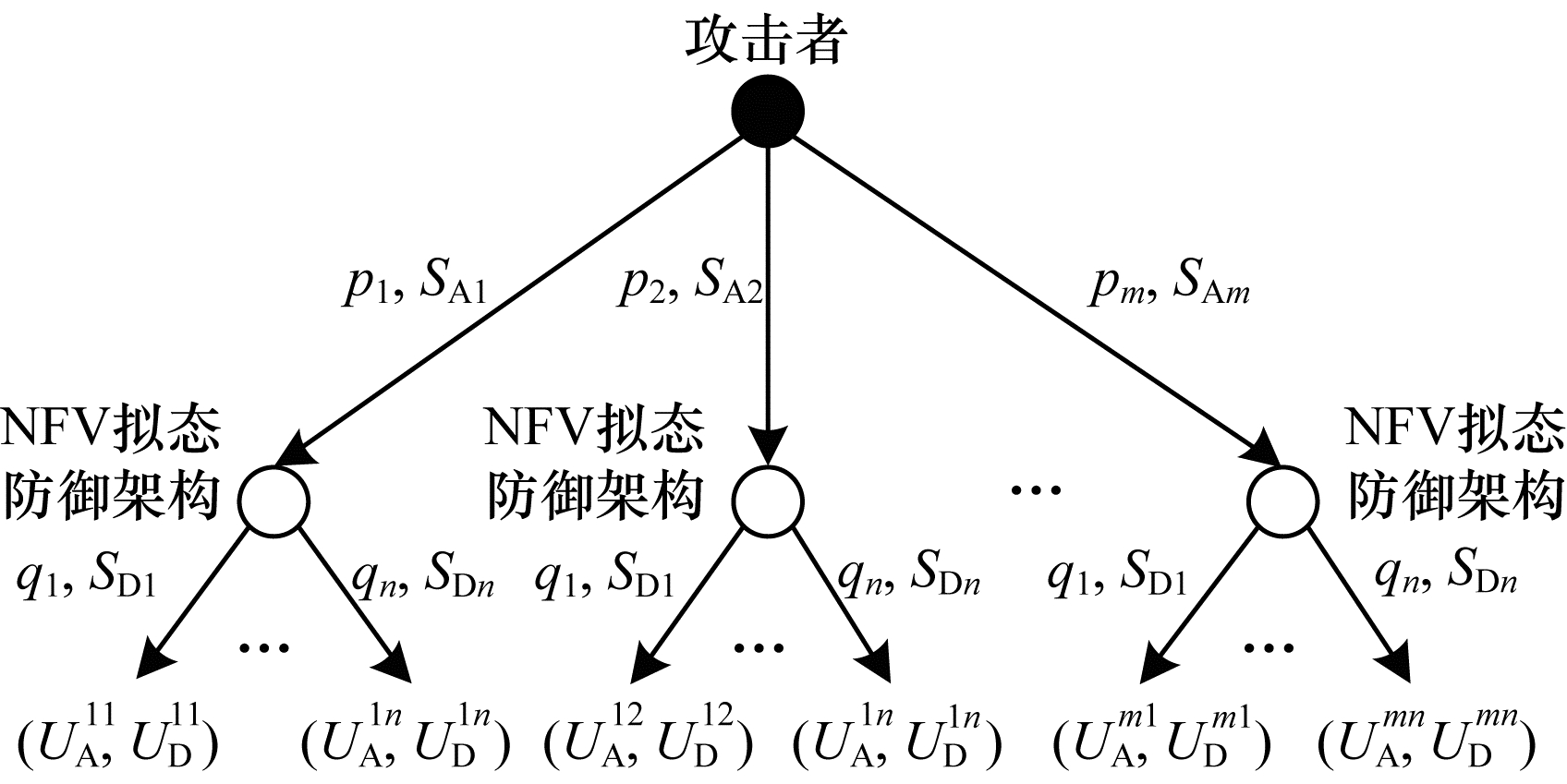
MSDSEGM模型对应的攻防博弈树如图 2所示,由图可知攻击者和NFV拟态防御架构采取不同攻防策略时得到的攻防收益也会不同。该收益不仅与其自身的策略有关,而且还与对方的策略密切相关。
|
Download:
|
| 图 2 网络攻防博弈树 Fig. 2 Network attack and defense game tree | |
对攻击者和防御者的博弈收益进行量化是MSDSEGM模型演化均衡求解和稳定性分析的基础,其量化是否合理直接决定最终博弈结果的准确性。文献[12]在总结多种攻击防御策略分类的基础上,提出了成本/回报量化方法,即收益为回报减去成本。基于此,在对MSDSEGM模型进行分析之前,结合NFV拟态防御架构的特点给出以下关于攻防双方收益的定义。
定义2(攻击成本AC) 攻击者发动一次攻击所需耗费的时间开销、软硬件资源开销、风险开销等。
定义3(攻击回报
定义4(防御成本
| $ {D}_{\mathrm{C}}=\alpha \times {O}_{\mathrm{C}}+{N}_{\mathrm{C}} $ | (2) |
其中:
定义5(防御损失
| $ {D}_{\mathrm{L}}=\beta \times \mu \times {V}_{\mathrm{L}}+{F}_{\mathrm{L}} $ | (3) |
由式(3)可知,防御损失由漏洞损失
定义6(防御回报
定义7(底层负载
根据上述定义,可以得到博弈收益函数的具体表达式:
| $ {U}_{\mathrm{A}}^{ij}={A}_{\mathrm{R}}-{A}_{\mathrm{C}} $ | (4) |
| $ {U}_{\mathrm{D}}^{ij}=N\times {D}_{\mathrm{R}}-{D}_{\mathrm{C}}-{D}_{\mathrm{L}}-{U}_{\mathrm{L}} $ | (5) |
本节涉及的相关变量及含义如表 1所示。

|
下载CSV 表 1 主要变量及含义 Table 1 Main variables and their significance |
本节使用复制动态(Replicator Dynamics,RD)方法对MSDSEGM模型进行演化均衡求解。复制动态方程就是策略选取概率的动态变化速率,描述的是博弈过程中攻防策略随时间的动态调整过程,是目前应用最为广泛的一种动力学演化机制[14]。由于在有限理性的条件下博弈参与者掌握的初始知识是有限的,因此采取的策略并非完全理性条件下的最优策略,在博弈的过程中通过不断调整和改进,收益低的策略的选取概率逐渐降低,收益高的策略的选取概率逐渐提高,最终达到策略均衡的结果。
采用复制动态方程求解MSDSEGM模型演化均衡的具体过程为:
1)根据攻防策略概率集合
| $ {U}_{\mathrm{A}i}={q}_{1}{U}_{\mathrm{A}}^{i1}+{q}_{2}{U}_{\mathrm{A}}^{i2}+\cdots +{q}_{n}{U}_{\mathrm{A}}^{in}=\sum \limits_{j=1}^{n}{q}_{j}{U}_{\mathrm{A}}^{ij} $ | (6) |
| $ {U}_{\mathrm{A}}={p}_{1}{U}_{\mathrm{A}1}+{p}_{2}{U}_{\mathrm{A}2}+\cdots +{p}_{m}{U}_{\mathrm{A}m}=\sum\limits _{i=1}^{m}{p}_{i}{U}_{\mathrm{A}i} $ | (7) |
2)计算攻击者的复制动态方程:
| $ A\left({p}_{i}\right)=\frac{\mathrm{d}{p}_{i}\left(t\right)}{\mathrm{d}t}={p}_{i}\left(t\right)({U}_{\mathrm{A}i}-{U}_{\mathrm{A}}) $ | (8) |
其中:
3)根据攻防策略概率集合
| $ {U}_{\mathrm{D}j}={p}_{1}{U}_{\mathrm{D}}^{1j}+{p}_{2}{U}_{\mathrm{D}}^{2j}+\cdots +{p}_{m}{U}_{\mathrm{D}}^{mj}=\sum \limits_{i=1}^{m}{p}_{i}{U}_{\mathrm{D}}^{ij} $ | (9) |
| $ {U}_{\mathrm{D}}={q}_{1}{U}_{\mathrm{D}1}+{q}_{2}{U}_{\mathrm{D}2}+\cdots +{q}_{n}{U}_{\mathrm{D}n}=\sum \limits_{j=1}^{n}{q}_{j}{U}_{\mathrm{D}j} $ | (10) |
4)计算NFV拟态防御架构的复制动态方程:
| $ D\left({q}_{j}\right)=\frac{\mathrm{d}{q}_{j}\left(t\right)}{\mathrm{d}t}={q}_{j}\left(t\right)({U}_{\mathrm{D}j}-{U}_{\mathrm{D}}) $ | (11) |
其中:
5)联立攻击者与NFV拟态防御架构的复制动态方程进行演化均衡求解:
| $ \left\{\begin{array}{l}\begin{array}{l}\begin{array}{l}A\left({p}_{1}\right)=\frac{\mathrm{d}{p}_{1}\left(t\right)}{\mathrm{d}t}={p}_{1}\left(t\right)({U}_{\mathrm{A}1}-{U}_{\mathrm{A}})=0\\ \vdots \end{array}\\ A\left({p}_{m}\right)=\frac{\mathrm{d}{p}_{m}\left(t\right)}{\mathrm{d}t}={p}_{m}\left(t\right)({U}_{\mathrm{A}m}-{U}_{\mathrm{A}})=0\end{array}\\ D\left({q}_{1}\right)=\frac{\mathrm{d}{q}_{1}\left(t\right)}{\mathrm{d}t}={q}_{1}\left(t\right)({U}_{\mathrm{D}1}-{U}_{\mathrm{D}})=0\\ \vdots \\ D\left({q}_{n}\right)=\frac{\mathrm{d}{q}_{n}\left(t\right)}{\mathrm{d}t}={q}_{n}\left(t\right)({U}_{\mathrm{D}n}-{U}_{\mathrm{D}})=0\end{array}\right. $ | (12) |
对式(12)进行求解,可以得到MSDSEGM模型的演化均衡策略,即在该策略下各个博弈行为的选择概率不变。但是其中的一些演化均衡策略存在不稳定性,即一旦发生博弈双方的策略偏离该均衡状态的情况,复制动态方程就会使演化结果不再收敛于该策略。因此,需要对演化均衡策略进行稳定性分析,得到演化均衡策略中的稳定策略,实现最优动态调度策略选取。
2.4 演化稳定策略演化稳定策略(Evolutionarily Stable Strategy,ESS)是演化博弈中的一个核心概念[15],是对纳什均衡的改进,具有较强的稳定性和预测能力,其在受到少量干扰后仍能恢复。演化稳定策略的数学定义为:
定义8 如果
| $ U\left[x, { \varepsilon }_{y}+(1- \varepsilon )x\right] > U\left[y, { \varepsilon }_{y}+(1- \varepsilon )x\right] $ | (13) |
其中:
针对2.3节采用复制动态方程求出的演化均衡策略,利用李雅普诺夫间接法[16]对其进行稳定性分析。由于式(12)是一个非线性微分方程组并且二阶连续可微,因此可以通过研究其在均衡点
| $ \left\{\begin{array}{l}A\left({p}_{1}\right)=A\left({p}_{1}\right)\left|{}_{\boldsymbol{O}}\right.+\frac{\partial A\left({p}_{1}\right)}{\partial {p}_{1}}\left(\boldsymbol{O}\right)({p}_{1}-{p}_{O1})+\cdots +\frac{\partial A\left({p}_{1}\right)}{\partial {p}_{m}}\left(\boldsymbol{O}\right)({p}_{m}-{p}_{Om})+\frac{\partial A\left({p}_{1}\right)}{\partial {q}_{1}}\left(\boldsymbol{O}\right)({q}_{1}-{q}_{O1})+\cdots +\\ \frac{\partial A\left({p}_{1}\right)}{\partial {q}_{n}}\left(\boldsymbol{O}\right)({q}_{n}-{q}_{On})+{\xi }_{1}({p}_{1}, {p}_{2}, \cdots , {p}_{m}, {q}_{1}, {q}_{2}, \cdots , {q}_{n})\\ \vdots \\ A\left({p}_{m}\right)=A\left({p}_{m}\right)\left|{}_{\boldsymbol{O}}\right.+\frac{\partial A\left({p}_{m}\right)}{\partial {p}_{1}}\left(\boldsymbol{O}\right)({p}_{1}-{p}_{O1})+\cdots +\frac{\partial A\left({p}_{m}\right)}{\partial {p}_{m}}\left(\boldsymbol{O}\right)({p}_{m}-{p}_{Om})+\frac{\partial A\left({p}_{m}\right)}{\partial {q}_{1}}\left(\boldsymbol{O}\right)({q}_{1}-{q}_{O1})+\cdots +\\ \frac{\partial A\left({p}_{m}\right)}{\partial {q}_{n}}\left(\boldsymbol{O}\right)({q}_{n}-{q}_{On})+{\xi }_{m}({p}_{1}, {p}_{2}, \cdots , {p}_{m}, {q}_{1}, {q}_{2}, \cdots , {q}_{n})\\ D\left({q}_{1}\right)=D\left({q}_{1}\right)\left|{}_{\boldsymbol{O}}\right.+\frac{\partial D\left({q}_{1}\right)}{\partial {p}_{1}}\left(\boldsymbol{O}\right)({p}_{1}-{p}_{O1})+\cdots +\frac{\partial D\left({q}_{1}\right)}{\partial {p}_{m}}\left(\boldsymbol{O}\right)({p}_{m}-{p}_{Om})+\frac{\partial D\left({q}_{1}\right)}{\partial {q}_{1}}\left(\boldsymbol{O}\right)({q}_{1}-{q}_{O1})+\cdots +\\ \frac{\partial D\left({q}_{1}\right)}{\partial {q}_{n}}\left(\boldsymbol{O}\right)({q}_{n}-{q}_{On})+{\zeta }_{1}({p}_{1}, {p}_{2}, \cdots , {p}_{m}, {q}_{1}, {q}_{2}, \cdots , {q}_{n})\\ \vdots\\ D\left({q}_{n}\right)=D\left({q}_{n}\right)\left|{}_{\boldsymbol{O}}\right.+\frac{\partial D\left({q}_{n}\right)}{\partial {p}_{1}}\left(\boldsymbol{O}\right)({p}_{1}-{p}_{O1})+\cdots +\frac{\partial D\left({q}_{n}\right)}{\partial {p}_{m}}\left(\boldsymbol{O}\right)({p}_{m}-{p}_{Om})+\frac{\partial D\left({q}_{n}\right)}{\partial {q}_{1}}\left(\boldsymbol{O}\right)({q}_{1}-{q}_{O1})+\cdots +\\ \frac{\partial D\left({q}_{n}\right)}{\partial {q}_{n}}\left(\boldsymbol{O}\right)({q}_{n}-{q}_{On})+{\zeta }_{n}({p}_{1}, {p}_{2}, \cdots , {p}_{m}, {q}_{1}, {q}_{2}, \cdots , {q}_{n})\end{array}\right. $ | (14) |
其中:
| $ \boldsymbol{x}=[{p}_{1}, {p}_{2}, \cdots , {p}_{m}, {q}_{1}, {q}_{2}, \cdots , {q}_{n}{]}^{\mathrm{T}} $ | (15) |
| $ \boldsymbol{f}=\left[A\right({p}_{1}), A({p}_{2}), \cdots , A({p}_{m}), D({q}_{1}), D({q}_{2}), \cdots , D({q}_{n}{\left)\right]}^{\mathrm{T}} $ | (16) |
| $ {\boldsymbol{f}}_{\boldsymbol{O}}=\left[A\right({p}_{1})\left|{}_{\boldsymbol{O}}\right., \cdots , A({p}_{m}\left)\left|{}_{\boldsymbol{O}}, D\left({q}_{1}\right)\left|{}_{\boldsymbol{O}}\right., \cdots , \right.D\right({q}_{n}{\left)\left|{}_{\boldsymbol{O}}\right.\right]}^{\mathrm{T}} $ | (17) |
令
| $ \boldsymbol{J}=\\ \left(\begin{array}{cccc}\begin{array}{cc}\begin{array}{c}\frac{\partial A\left({p}_{1}\right)}{\partial {p}_{1}}\\ \vdots \end{array}& \begin{array}{c}\cdots \\ \end{array}\end{array}& \begin{array}{c}\frac{\partial A\left({p}_{1}\right)}{\partial {p}_{m}}\\ \vdots \end{array}& \begin{array}{cc}\begin{array}{c}\frac{\partial A\left({p}_{1}\right)}{\partial {q}_{1}}\\ \vdots \end{array}& \begin{array}{c}\cdots \\ \end{array}\end{array}& \begin{array}{c}\frac{\partial A\left({p}_{1}\right)}{\partial {q}_{n}}\\ \vdots \end{array}\\ \begin{array}{cc}\frac{\partial A\left({p}_{m}\right)}{\partial {p}_{1}}& \cdots \end{array}& \frac{\partial A\left({p}_{m}\right)}{\partial {p}_{m}}& \begin{array}{cc}\frac{\partial A\left({p}_{m}\right)}{\partial {q}_{1}}& \cdots \end{array}& \frac{\partial A\left({p}_{m}\right)}{\partial {q}_{n}}\\ \begin{array}{cc}\begin{array}{c}\frac{\partial D\left({q}_{1}\right)}{\partial {p}_{1}}\\ \vdots \end{array}& \begin{array}{c}\cdots \\ \end{array}\end{array}& \begin{array}{c}\frac{\partial D\left({q}_{1}\right)}{\partial {p}_{m}}\\ \vdots \end{array}& \begin{array}{cc}\begin{array}{c}\frac{\partial D\left({q}_{1}\right)}{\partial {q}_{1}}\\ \vdots \end{array}& \begin{array}{c}\cdots \\ \end{array}\end{array}& \begin{array}{c}\frac{\partial D\left({q}_{1}\right)}{\partial {q}_{n}}\\ \vdots \end{array}\\ \begin{array}{cc}\frac{\partial D\left({q}_{n}\right)}{\partial {p}_{1}}& \cdots \end{array}& \frac{\partial D\left({q}_{n}\right)}{\partial {p}_{m}}& \begin{array}{cc}\frac{\partial D\left({q}_{n}\right)}{\partial {q}_{1}}& \cdots \end{array}& \frac{\partial D\left({q}_{n}\right)}{\partial {q}_{n}}\end{array}\right) $ | (18) |
当带入均衡点
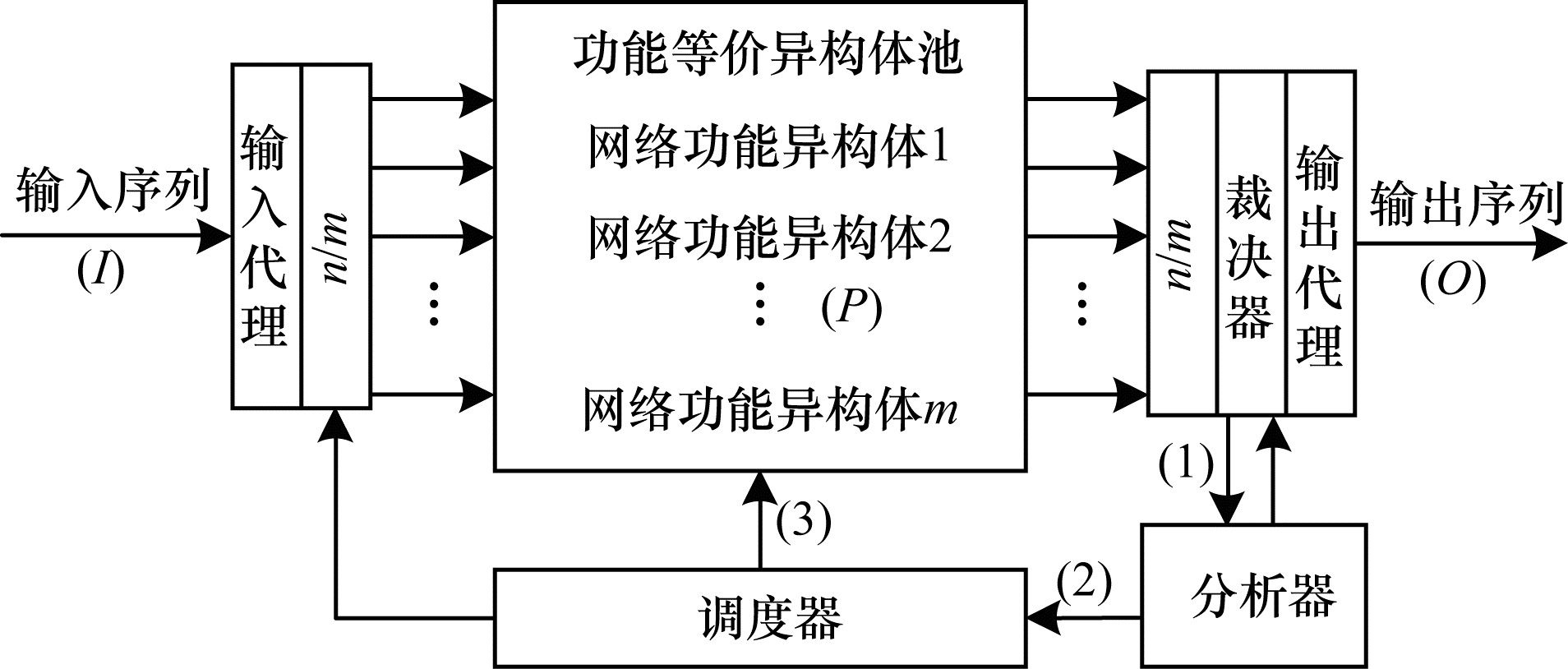
基于演化博弈的动态调度策略工作流程如图 3所示。
|
Download:
|
| 图 3 基于演化博弈的动态调度策略工作流程 Fig. 3 Workflow of dynamic scheduling strategy based on evolutionary game | |
1)分析器根据裁决结果,利用漏洞扫描、数据采集、查杀病毒木马、沙箱隔离等防护手段对异常执行体进行故障查找和安全问题排查,或利用态势感知和大数据分析技术对异常执行体的系统信息深入研究,得到当前环境下的攻防状态信息(攻击的类型和分布、各异构体对不同攻击的防御情况)。
2)调度器利用博弈论方法构建一个MSDSEGM模型,并根据拟态防御架构的系统组成(例如异构体的数量、异构体的组成构件、执行体的数量)和分析器中的反馈信息,得到攻防双方的策略集合、策略概率集合和收益函数集合,以及NFV拟态防御架构的状态集合。
3)调度器根据演化博弈理论,利用复制动态方程方法对异构体动态调度策略进行不断优化调整。
基于演化博弈的最优动态调度策略选取算法描述如下:
算法1 基于演化博弈的最优动态调度策略选取算法
输入 攻防双方状态信息
输出 动态调度策略
1.while攻防博弈未结束do
2.
3.
4.
5.
6.
7.
8.if
9.
10.
11.
12.
13.
14.
15.end;
16.end;
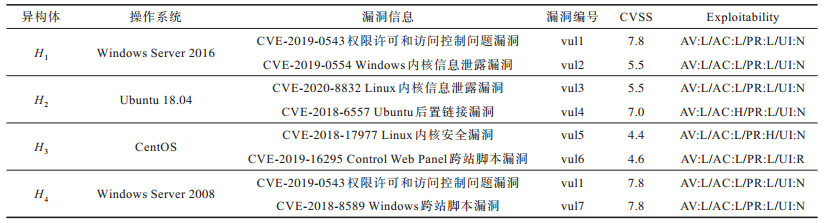
4 仿真结果与分析 4.1 仿真设置为验证MSDSEGM模型和最优调度策略选取算法的可行性和有效性,在MATLAB仿真平台上对博弈过程进行仿真与分析,仿真平台主机配置为Intel® CoreTM i7-7700 CPU 3.60 GHz,8 GB RAM。为便于展示分析,本节仅对异构体的操作系统层进行异构化。设定异构体数量为4,操作系统分别采用Windows Server 2016、Ubuntu 18.04、CentOS和Windows Server 2008。由通用漏洞披露(Common Vulnerabilities & Exposures,CVE)[17]和通用漏洞评分系统(Common Vulnerability Scoring System,CVSS)[18]得到异构体操作系统配置参数及相关漏洞信息,如表 2所示,其中CVSS分值反映了漏洞的严重程度,漏洞的得分最大为10,最小为0。CVSS得分在7~10的是高级漏洞,得分在4~6.9之间的是中级漏洞,得分在0~3.9的则是低级漏洞。Exploitability为CVSS中的可利用度指标,反映了漏洞受攻击的难易程度。从上述4个异构体中选择3个上线作为执行体,则NFV拟态防御架构共有
|
下载CSV 表 2 操作系统配置参数及漏洞信息 Table 2 Operating system configuration parameters and vulnerability information |
本节假设攻防双方在初始时刻对对方的信息均不了解,分别以
图 4和图 5分别为
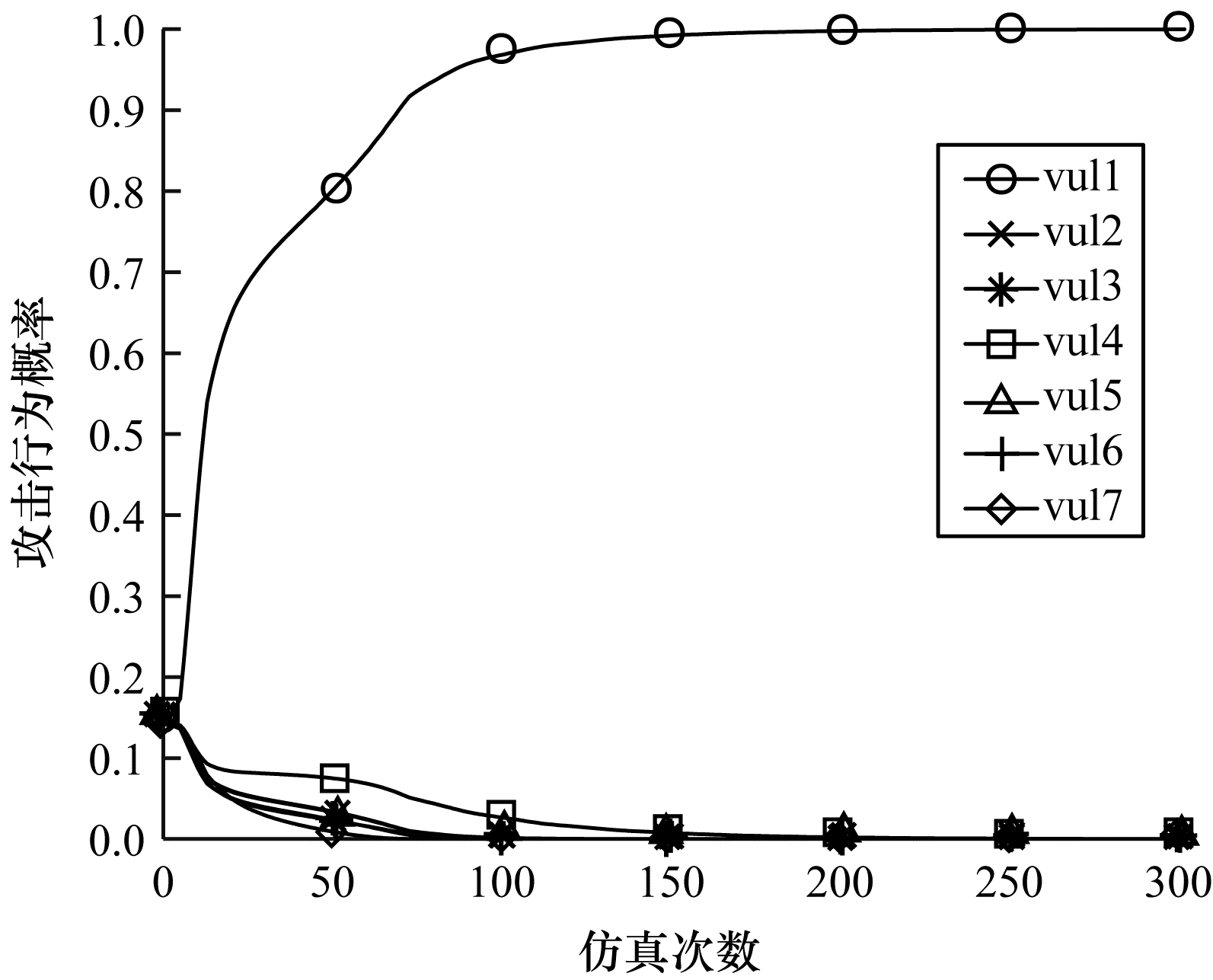
|
Download:
|
|
图 4 |
|
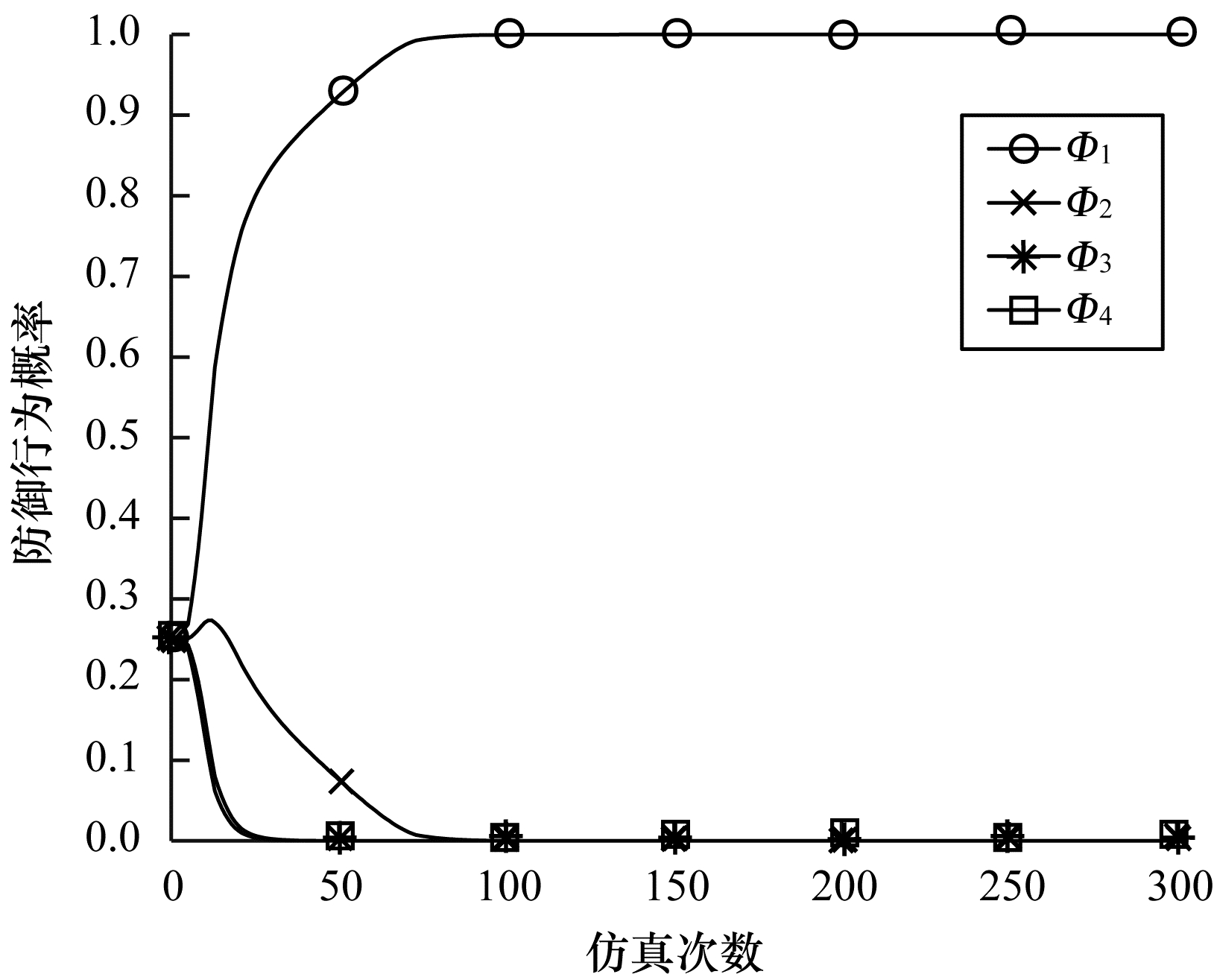
|
Download:
|
|
图 5 |
|
图 6和图 7分别为
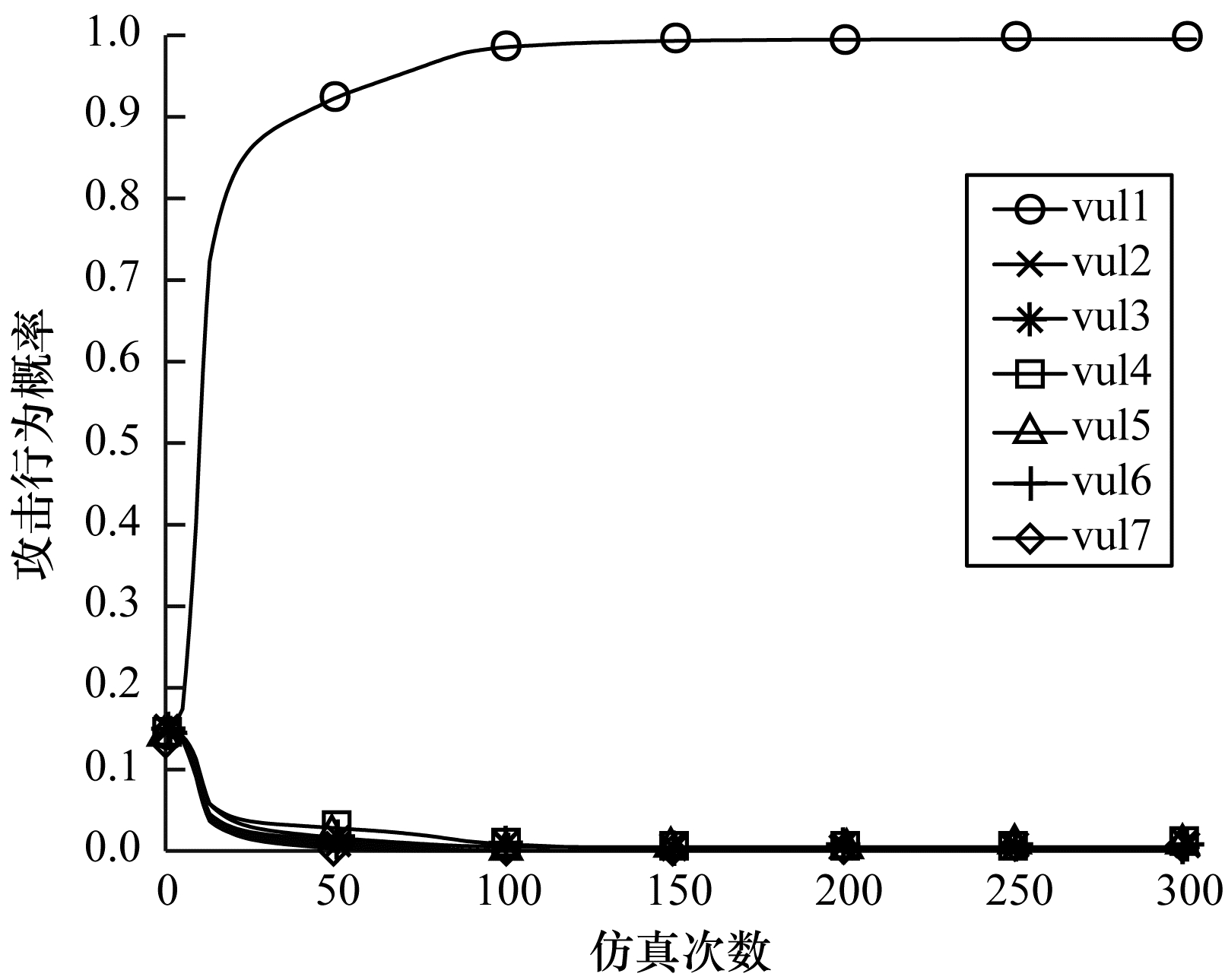
|
Download:
|
|
图 6 |
|
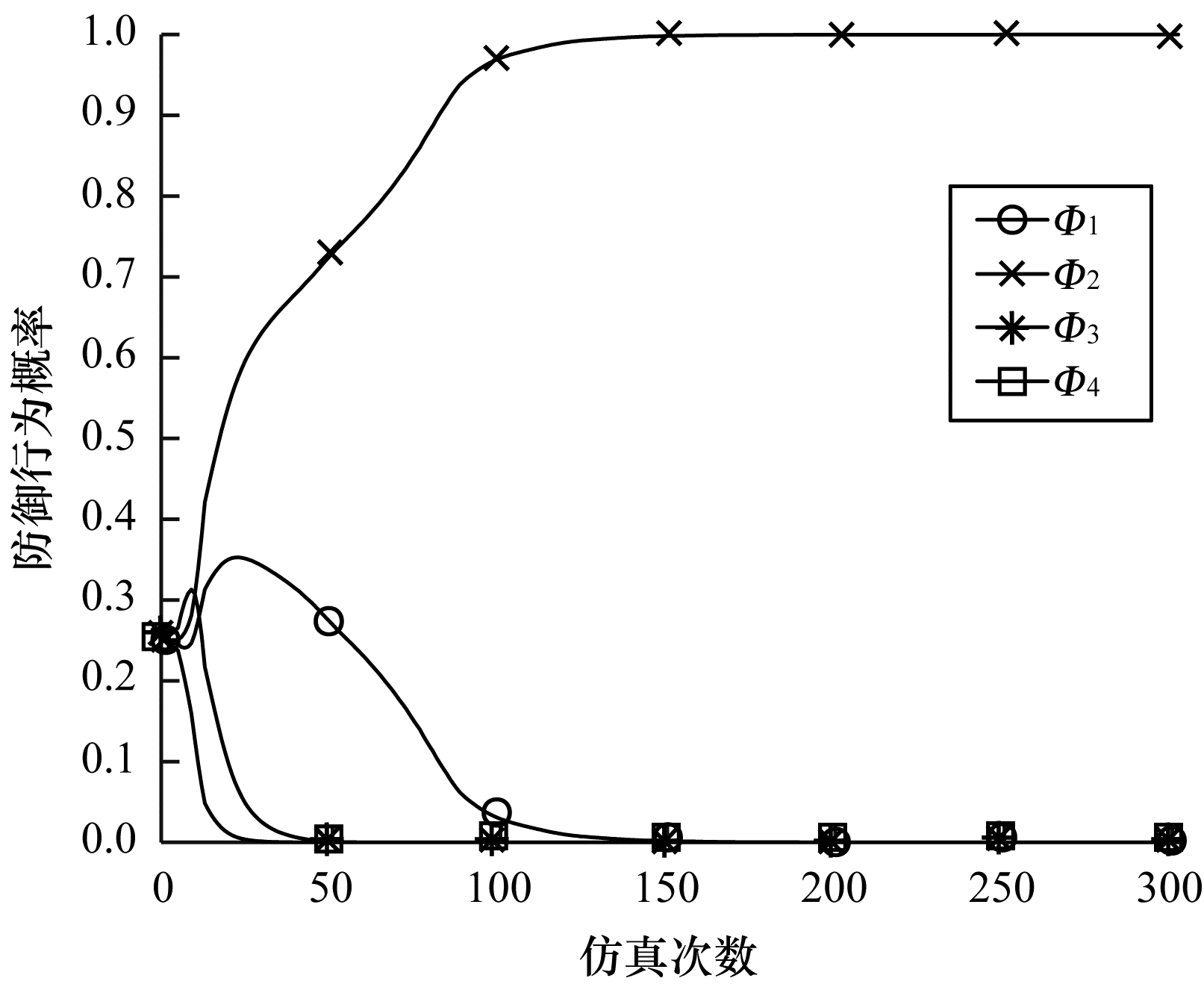
|
Download:
|
|
图 7 |
|
图 8和图 9分别为
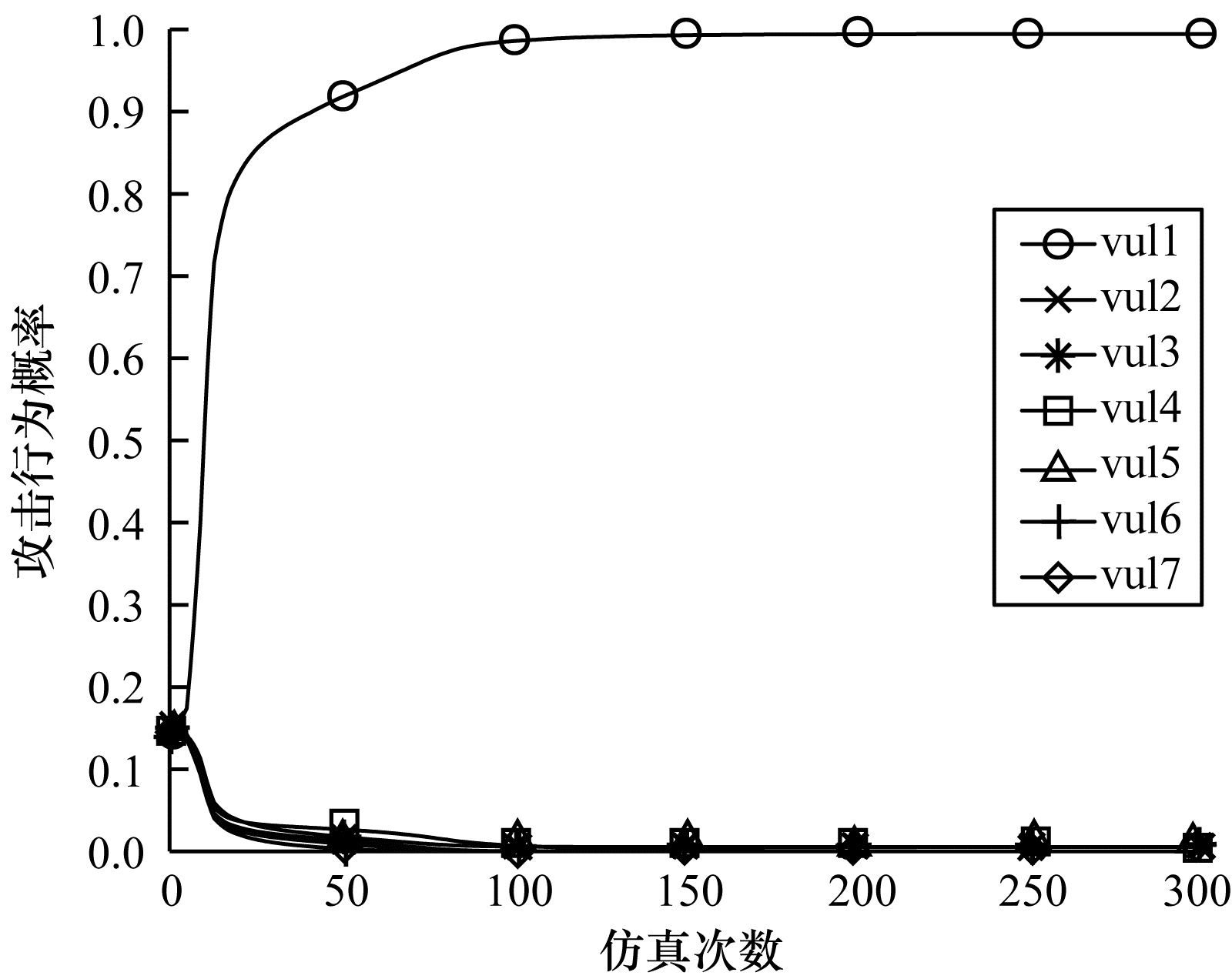
|
Download:
|
|
图 8 |
|
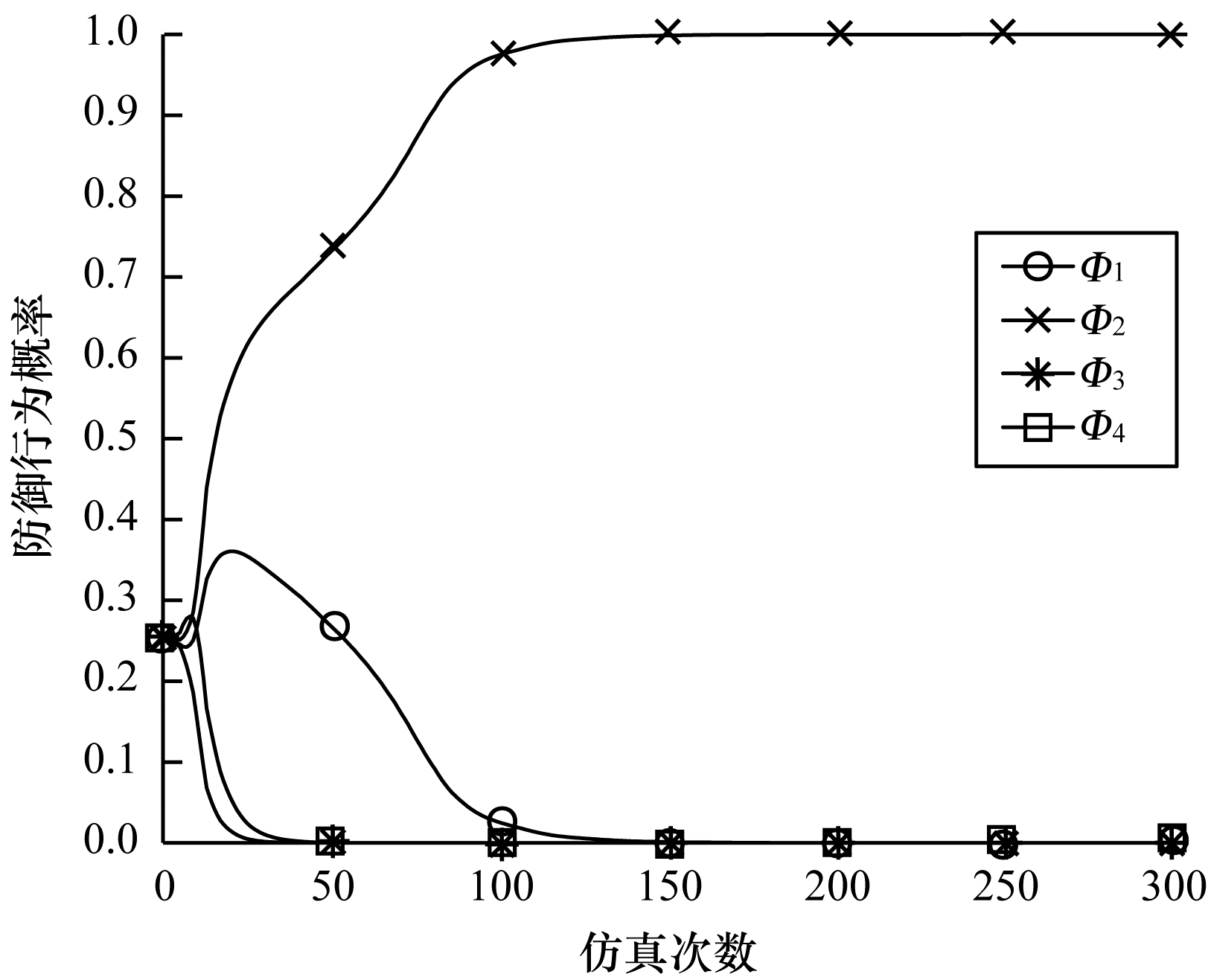
|
Download:
|
|
图 9 |
|
图 10和图 11分别为
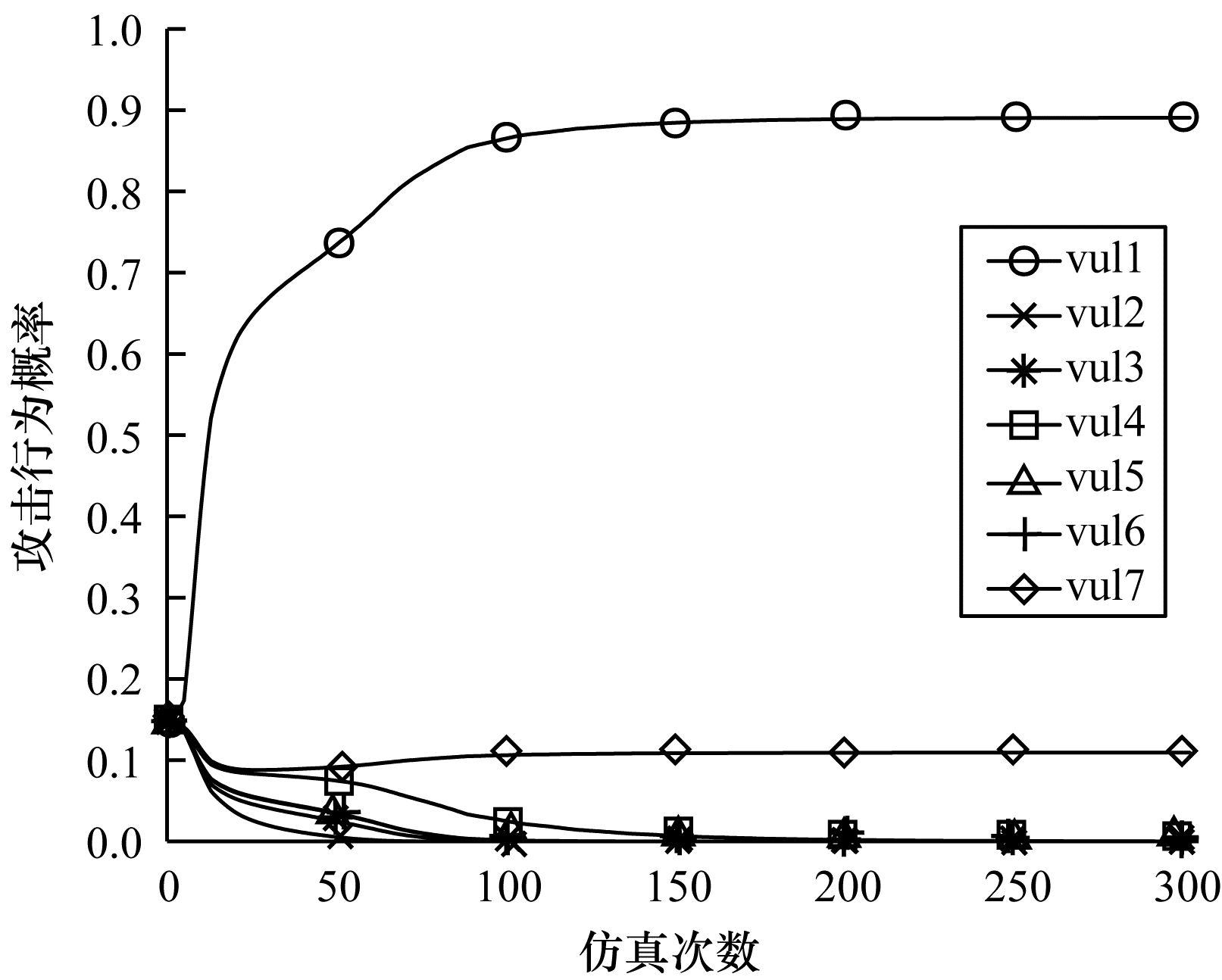
|
Download:
|
|
图 10 |
|
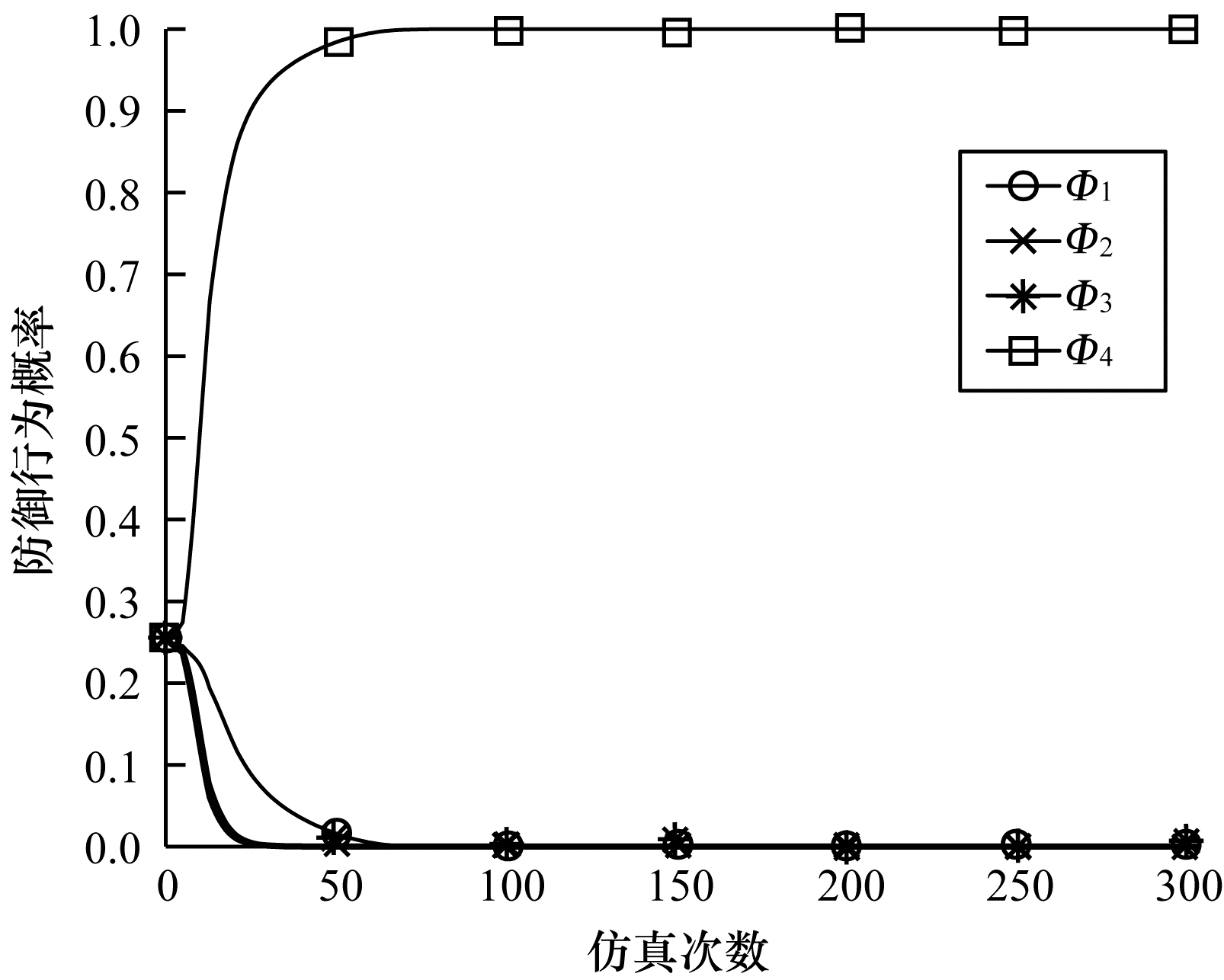
|
Download:
|
|
图 11 |
|
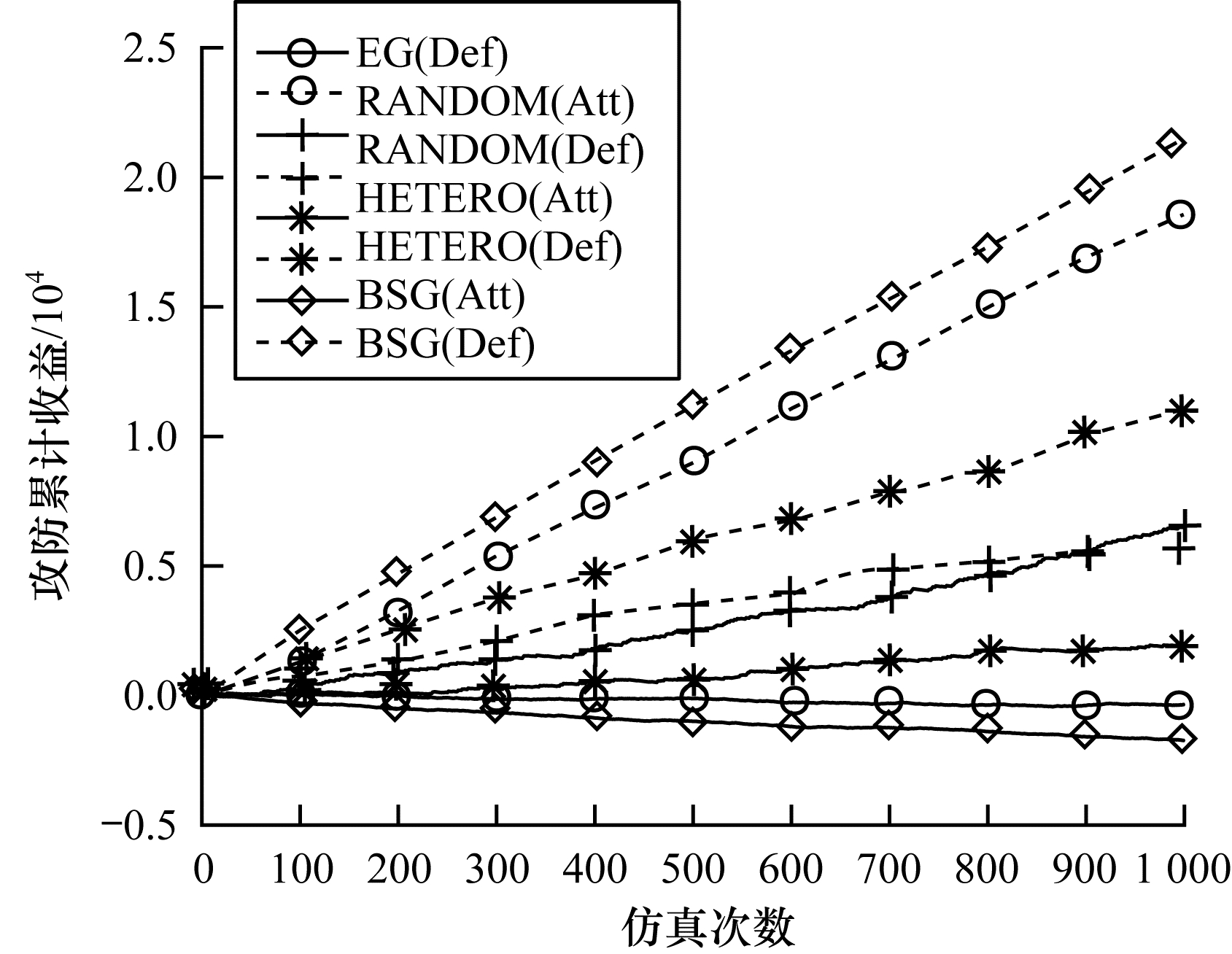
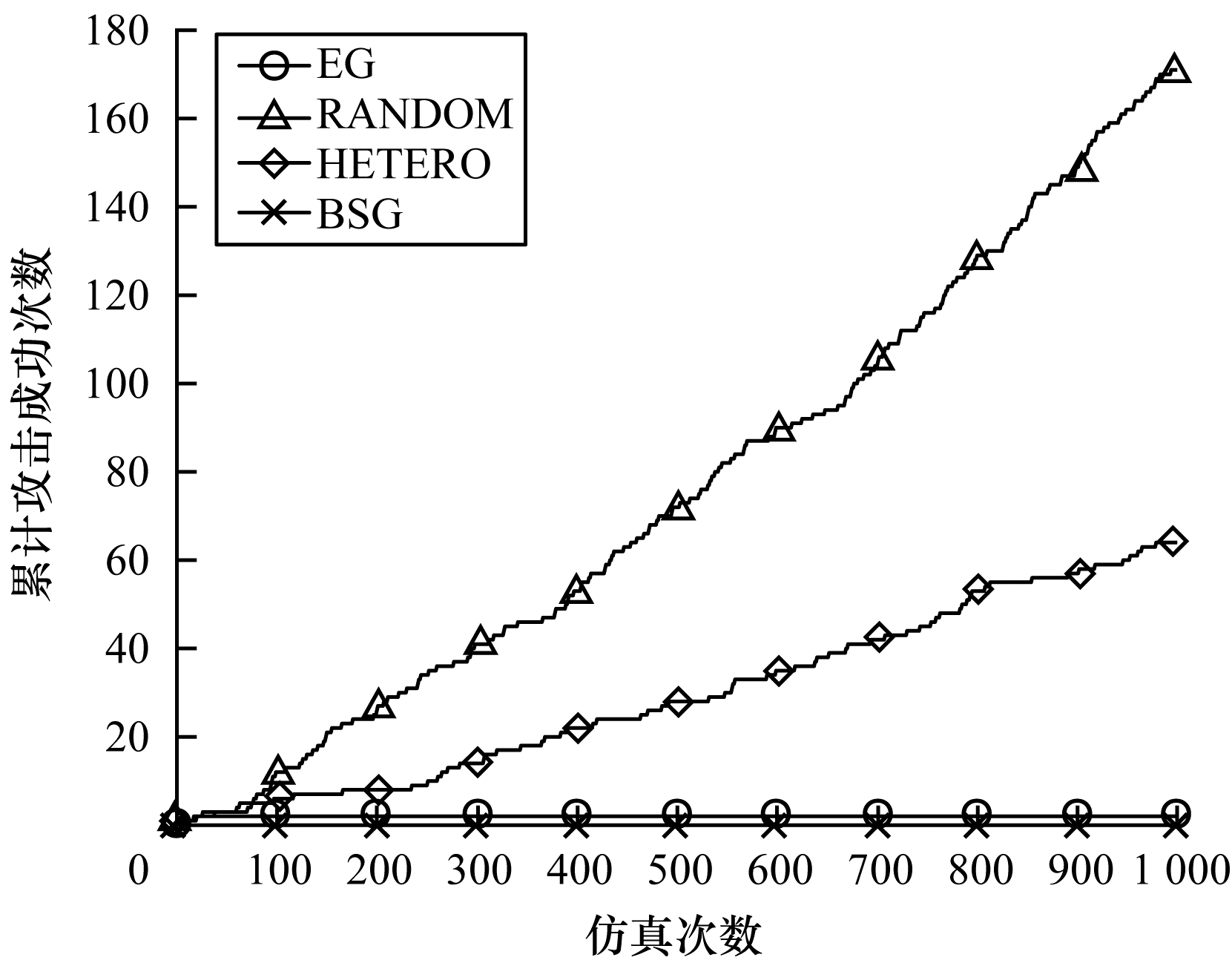
为展现本文提出的调度策略所带来的安全收益和防御效能情况,将本文提出的基于演化博弈的调度策略(EG)与随机调度策略[21](RANDOM)、基于执行体异构度的调度策略(HETERO)[6]以及基于Bayesian-Stackelberg博弈的调度策略[22](BSG)中攻防双方的累计博弈收益和攻击者累计攻击成功的次数进行对比,如图 12和图 13所示。
|
Download:
|
| 图 12 攻防累计收益对比 Fig. 12 Comparison of cumulative benefits of offense and defense | |
|
Download:
|
| 图 13 攻击者累计攻击成功次数 Fig. 13 Cumulative number of successful attacks by attacker | |
图 12为攻防累计收益对比图,其中:实线表示攻击者(Att)的累计收益;虚线表示防御者(Def)的累计收益。如图所示,EG和BSG都是基于博弈论的调度策略,NFV拟态防御架构可以根据实际的网络攻防环境找到有针对性的调度策略,实现防御收益的大幅提升,同时将攻击者的收益降低到负值。BSG在基于攻防双方都是完全理性的前提下,可以在得到更多的防御收益的同时进一步降低攻击者的收益。EG需要通过不断学习与调整逐渐找到最佳调度策略,防御收益相比BSG略低,但更符合实际网络中攻防双方的认知规律。HETERO和RANDOM虽然增加了系统的动态性,但是不具有针对性,防御收益相对较低。HETERO是基于执行体异构度的调度策略,异构度越大的执行体调度上线的概率就越大,一定程度上降低了共模漏洞存在的可能性,因此,HETERO的防御收益高于RANDOM。
NFV拟态防御架构将静态空间的单一确定目标攻击难度增强为动态异构空间、多元目标协同一致攻击难度,难度等级呈非线性提升,使得攻击者利用共模漏洞攻击成功防御系统成为小概率事件。但为便于展示基于演化博弈的调度策略对系统防御效能的影响,本文将攻击者攻击成功NFV拟态防御架构的条件放宽为利用同一漏洞攻破半数以上的执行体,但不考虑是否输出相同的错误结果,并对不同调度策略下攻击者的累计攻击成功次数进行对比。如图 13所示,经过1 000次仿真后,HETERO策略下攻击者的累计攻击成功次数为64次,RANDOM策略下攻击者的累计攻击成功次数为171次,同时由于HETERO和RANDOM没有充分利用裁决机制对异常执行体的感知定位功能对调度策略进行有针对性的调整优化,因此随着仿真次数的增加,攻击者的累计攻击成功次数会持续增长。EG相比于HETERO和RANDOM提升了NFV拟态防御架构的安全性,在1 000次仿真过程中,攻击者仅在博弈初期攻击成功了2次,之后通过对分析器中的反馈信息不断学习,优化调度策略,使得累计攻击成功次数维持在该水平不变,有效提高了NFV拟态防御架构的防御效能。BSG基于攻防双方完全理性的前提,在博弈初期就可以找到最优调度策略,避免了攻击者成功攻击NFV拟态防御架构的情况,因此,攻击者的累计攻击成功次数始终为零。需要说明的是,图 13的仿真结果是基于本文的参数设置条件下产生的,而在实际的网络环境中,异构体之间由于组成结构不同,共模漏洞存在概率较低,攻击者利用共模漏洞攻击成功的次数将小于该值。
5 结束语现有拟态防御架构中的动态调度策略大多未利用裁决机制对异常执行体的定位感知能力进行优化调整,策略缺乏针对性和适应性。本文在NFV拟态防御架构中增加一个分析器,用于对历史裁决信息进行分析研究。在此基础上,利用分析器得到的反馈信息和演化博弈理论,从攻防双方的有限理性出发构建多状态动态调度演化博弈模型,采用复制动态方程和李雅普诺夫间接法对攻防双方的策略演化趋势和稳定性进行分析,提出一种基于演化博弈的最优动态调度策略选取算法。仿真结果表明,该算法可以根据拟态裁决的反馈结果,通过不断调整优化选择出具有针对性和适应性的调度策略,有效提升NFV拟态防御架构的安全收益和防御效能。本文对异构体的操作系统层做异构化处理,利用操作系统的具体漏洞信息对基于演化博弈的调度策略进行有效性分析。考虑到网络功能异构体由三层异构元素组成,下一步将对异构体的三层异构元素做异构化处理,并通过对漏洞进行分类来降低分析复杂度。
| [1] |
ETSI. Network Functions Virtualization(NFV): architectural framework[EB/OL]. (2014-12-01)[2021-03-24]. https://www.etsi.org/technologies/nfv.
|
| [2] |
FIROOZJAEI M D, JEONG J P, KO H, et al. Security challenges with network functions virtualization[J]. Future Generation Computer Systems, 2016, 67(2): 315-324. |
| [3] |
邬江兴. 网络空间拟态防御研究[J]. 信息安全学报, 2016, 1(4): 1-10. WU J X. Research on cyber mimic defense[J]. Journal of Cyber Security, 2016, 1(4): 1-10. (in Chinese) |
| [4] |
沈丛麒, 陈双喜, 吴春明. 基于信誉度与相异度的自适应拟态控制器研究[J]. 通信学报, 2018, 39(z2): 173-180. SHEN C Q, CHEN S X, WU C M. Adaptive mimic defensive controller framework based on reputation and dissimilarity[J]. Journal on Communications, 2018, 39(z2): 173-180. (in Chinese) |
| [5] |
顾泽宇, 张兴明, 林森杰. 基于安全策略的负载感知动态调度机制[J]. 计算机应用, 2017, 37(11): 3304-3310. GU Z Y, ZHANG X M, LIN S J. Load-aware dynamic scheduling mechanism based on security strategies[J]. Journal of Computer Applications, 2017, 37(11): 3304-3310. (in Chinese) |
| [6] |
刘勤让, 林森杰, 顾泽宇. 面向拟态安全防御的异构功能等价体调度算法[J]. 通信学报, 2018, 39(7): 192-202. LIU Q R, LIN S J, GU Z Y. Heterogeneous redundancies scheduling algorithm for mimic security defense[J]. Journal on Communications, 2018, 39(7): 192-202. (in Chinese) |
| [7] |
普黎明, 刘树新, 丁瑞浩, 等. 面向拟态云服务的异构执行体调度算法[J]. 通信学报, 2020, 41(3): 17-24. PU L M, LIU S X, DING R H, et al. Heterogeneous executor scheduling algorithm for mimic cloud service[J]. Journal on Communications, 2020, 41(3): 17-24. (in Chinese) |
| [8] |
盖伟麟, 辛丹, 王璐, 等. 态势感知中的数据融合和决策方法综述[J]. 计算机工程, 2014, 40(5): 21-25, 30. GAI W L, XIN D, WANG L, et al. Overview of data fusion and decision-making methods in situational awareness[J]. Computer Engineering, 2014, 40(5): 21-25, 30. (in Chinese) |
| [9] |
FRIEDMAN D. Evolutionary game in economics[J]. Econometrica, 1991, 59(3): 637-666. DOI:10.2307/2938222 |
| [10] |
黄健明, 张恒巍. 基于随机演化博弈模型的网络防御策略选取方法[J]. 电子学报, 2018, 46(9): 2222-2228. HUANG J M, ZHANG H W. A method for selecting defense strategies based on stochastic evolutionary game model[J]. Acta Electronica Sinica, 2018, 46(9): 2222-2228. (in Chinese) |
| [11] |
李鹤飞, 黄新力, 郑正奇. 基于软件定义网络的DDoS攻击检测方法及其应用[J]. 计算机工程, 2016, 42(2): 118-123. LI H F, HUANG X L, ZHENG Z Q. DDoS attack detection method based on software-defined network and its application[J]. Computer Engineering, 2016, 42(2): 118-123. (in Chinese) |
| [12] |
姜伟, 方滨兴, 田志宏, 等. 基于攻防博弈模型的网络安全测评和最优主动防御[J]. 计算机学报, 2009, 32(4): 817-827. JIANG W, FANG B X, TIAN Z H, et al. Evaluating network security and optimal active defense based on attack-defense game model[J]. Chinese Journal of Computers, 2009, 32(4): 817-827. (in Chinese) |
| [13] |
海梅生, 伊鹏, 江逸茗. 基于服务质量与资源约束的服务链部署策略[J]. 计算机工程, 2019, 45(3): 54-59. HAI M S, YI P, JIANG Y M. Service chain deployment strategy based on service quality and resource constraints[J]. Computer Engineering, 2019, 45(3): 54-59. (in Chinese) |
| [14] |
TAYLOR P D, JONKER L B. Evolutionarily stable strategies and game dynamics[J]. Mathematical Biosciences, 1978, 40(1/2): 145-156. |
| [15] |
SMITH J M, PRICE G R. The logic of animal conflict[J]. Nature, 1973, 246(5427): 15-18. DOI:10.1038/246015a0 |
| [16] |
ZAK S H. Systems and control[M]. Oxford, USA: Oxford University Press, 2003.
|
| [17] |
National Vulnerability Database. Common vulnerabilities and exposures[EB/OL]. [2020-12-03]. https://nvd.nist.gov.
|
| [18] |
OU X, SINGHAL A. The common vulnerability scoring system(CVSS)[EB/OL]. [2020-12-03]. http://forms.first.org/cvss/cvss_basic-2.0.pdf.
|
| [19] |
高妮, 高岭, 贺毅岳, 等. 基于贝叶斯攻击图的动态安全风险评估模型[J]. 四川大学学报(工程科学版), 2016, 48(1): 111-118. GAO N, GAO L, HE Y Y, et al. Dynamic security risk assessment model based on Bayesian attack graph[J]. Journal of Sichuan University (Engineering Science Edition), 2016, 48(1): 111-118. (in Chinese) |
| [20] |
姜伟, 方滨兴, 田志宏, 等. 基于攻防随机博弈模型的防御策略选取研究[J]. 计算机研究与发展, 2010, 47(10): 1714-1723. JIANG W, FANG B X, TIAN Z H, et al. Research on defense strategies selection based on attack-defense stochastic game model[J]. Journal of Computer Research and Development, 2010, 47(10): 1714-1723. (in Chinese) |
| [21] |
邬江兴, 李军飞, 张帆, 等. 一种异构功能等价体调度装置及方法: CN106161417A[P]. 2016-11-23. WU J X, LI J F, ZHANG F, et al. A heterogeneous redundancies scheduling equipment and method: CN106161417A[P]. 2016-11-23. |
| [22] |
王晓梅, 杨文晗, 张维, 等. 基于BSG的拟态Web服务器调度策略研究[J]. 通信学报, 2018, 39(z2): 112-120. WANG X M, YANG W H, ZHANG W, et al. Research on scheduling strategy of mimic Web server based on BSG[J]. Journal on Communications, 2018, 39(z2): 112-120. (in Chinese) |
 2022, Vol. 48
2022, Vol. 48
