密码设备在数据加密过程中通常会有功耗[1]、时间[2]和电磁辐射[3]等侧信道信息泄漏。侧信道攻击(Side Channel Attack, SCA)即利用泄漏的侧信道信息攻击密码设备, 采用数学统计分析方法计算泄漏信息与加密数据(或者解密数据)之间的关系以破解密钥。功耗攻击是侧信道攻击的一种, 其中, BRIER等人在2004年提出的相关功耗攻击(Correlation Power Attack, CPA)[4]因具有较强攻击性和密钥破解高效性被广泛应用。
在实施侧信道攻击前, 通常要对密码设备泄漏信息进行采样, 采样数据的纯净度与攻击效率和密钥破解正确率密切相关。在实际功耗攻击中, 采集功耗信息会受到环境噪声、热噪声和算法噪声等干扰, 而噪声在一定程度上会降低功耗攻击效率与密钥破解正确率, 甚至导致攻击失败。为消除噪声影响, 提高采样信号质量, 研究人员采用多种方法对数据降噪。文献[5]用估计的4阶累积量代替原始信号来执行传统CPA和差分功耗攻击(Differential Power Attack, DPA)以提高攻击性能。文献[6]利用小波变换对功耗曲线进行对准, 增强功耗的信噪比信息, 提高了DPA的攻击效率。文献[7]提出一种基于信息论的特殊降噪阈值, 但其在功耗数据降噪方面不具备普遍性。文献[8]通过仿真验证了小波变换的降噪效率要优于高阶累积量。基于小波变换的去噪过程能较好地表征以低频信息为主的信号, 但其忽略高频信息, 不能很好地分解包含大量细节信息的信号, 在表征数据细节信息方面存在一定缺陷[9]。针对小波变换无法处理高频信号的问题, 文献[10]在进行数据预处理时使用小波包阈值法对数据降噪, 从而提高功耗攻击效率。在实际采用小波包阈值对不同功耗数据降噪时, 阈值选取通常随功耗数据特征而变化, 并会影响到小波包降噪性能。此外, 小波包阈值只对低频信息降噪, 忽略了高频信息中仍存在噪声含量, 从而降低功耗数据质量。
针对上述问题, 本文提出一种改进的小波包分解降噪方法。采用奇异谱分析(Singular Spectrum Analysis, SSA)[11]通过奇异值分解将复杂信号分为不同的子序列。奇异谱分析与主成分分析[12]不同, 可基于特殊的矩阵结构处理单次功耗数据, 因此将奇异谱分析用于处理小波包分解的低频部分和高频部分, 并依据奇异熵的波动趋势[13]自适应地从各部分提取功耗信息, 以提高功耗数据的质量与纯净度。在此基础上, 使用原始功耗数据以及改进前后的小波包降噪功耗数据对硬件实现的SM4算法进行选择明文攻击, 对所得相关功耗攻击的攻击效率和密钥破解准确率进行对比分析。
1 基础知识 1.1 相关功耗攻击的原理与流程侧信道攻击中相关功耗攻击方法是利用真实功耗数据与模拟功耗数据之间线性关系来破解密钥, 该方法包括以下4个步骤:
1) 选取N组不同明文(或者密文)通过密码设备进行加密(或者解密)操作, 采集密码设备的功耗曲线, 记为P。
2) 选取中间值函数f(d, k), 中间值函数的选取与部分密钥和部分明文(或者密文)有关, 然后猜测密钥, 通过中间值函数计算对应中间值, 根据中间值的汉明重量模型或者汉明距离模型, 计算模拟功耗数据, 记为H。
3) 根据式(1)将真实功耗P与模拟功耗H按列求出相关系数ρ, 最后得到相关系数矩阵R。
| $ \rho (P,H) = \frac{{E(P,H) - E(P)E(H)}}{{\sqrt { {\rm{Var}} (P) {\rm{Var}} (H)} }} $ | (1) |
4) 观察矩阵R中各值, 其中最大值对应的猜测密钥即为破解的正确密钥[14]。
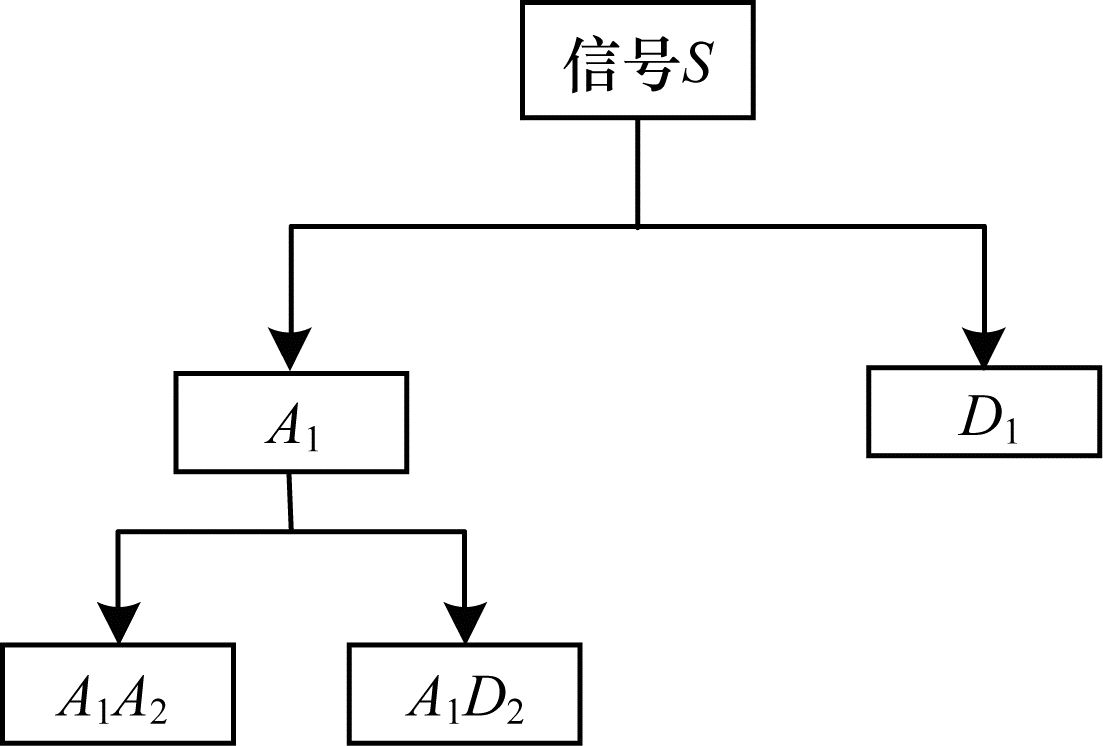
1.2 小波包分解小波变换(Wavelet Transform, WT)方法是基于傅里叶变换、泛函数分析、数值分析等数学分析方法提出的一种信号分析与处理方法, 广泛应用于信号处理、图像分析、语音处理等领域[15]。小波变换方法根据频率不同, 通过对小波基采取伸缩和平移等操作对信号进行多尺度精细化分析, 从而实现对信号时域和频域的局部变换, 提取信号中有效信息。信号S的两层小波分解流程如图 1所示。其中:A为信号低频数据(即近似部分), 为信号的主要信息; D为信号高频数据(即细节部分), 为信号的次要信息, 通常被视为噪声。由图 1可知, 小波变换方法只是针对信号低频数据, 而忽略信号高频数据[16], 这导致小波变换无法充分表征包含高频数据的信号, 因此小波变换方法去噪存在一定缺陷。
|
Download:
|
| 图 1 信号S的两层小波分解流程 Fig. 1 Two-layer wavelet decomposition flow of signal S | |
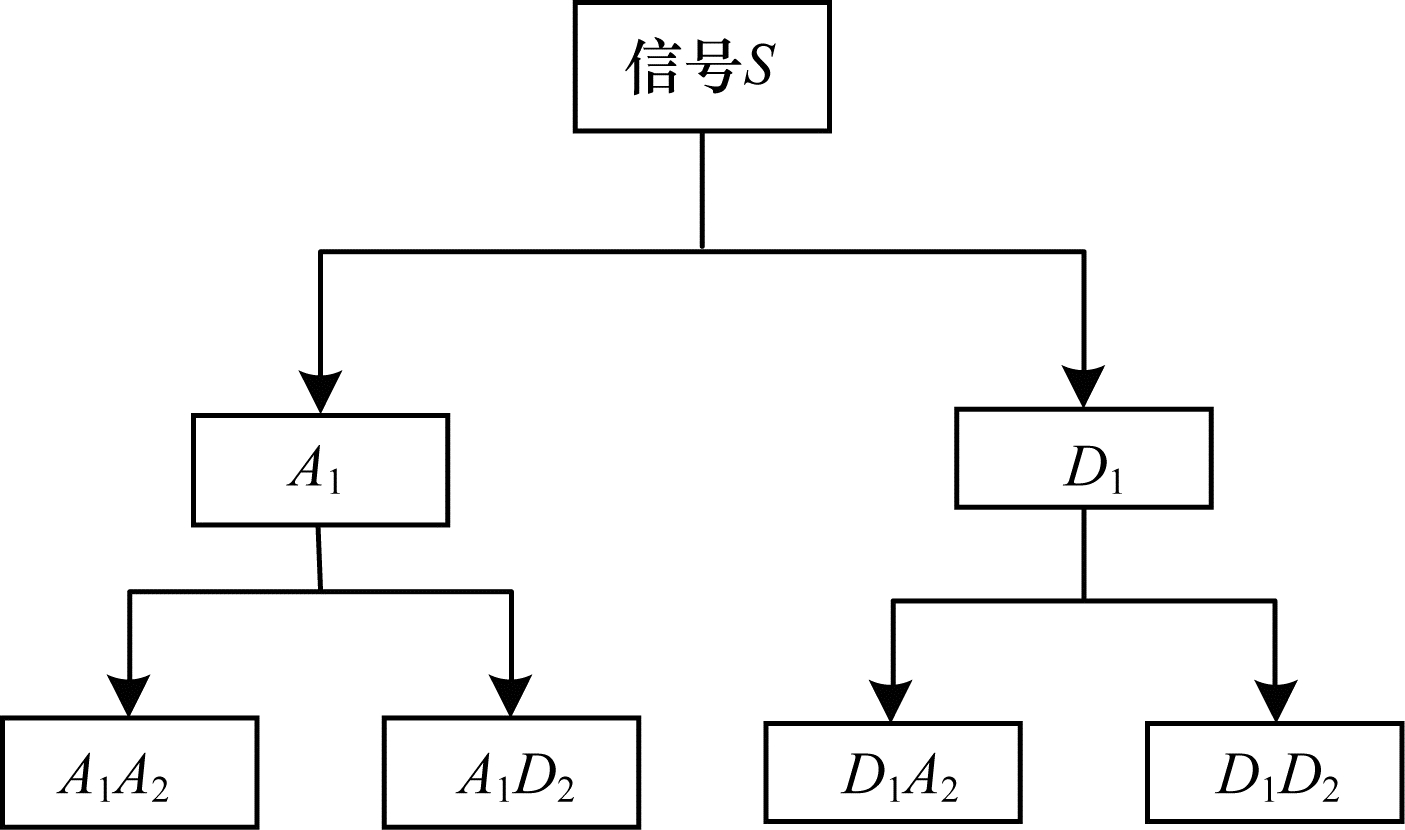
小波包变换(Wavelet Packet Transform, WPT)方法是对小波变换方法的提升与改进[17], 其基本思想是让信息能量集中, 在细节中寻找有序性并筛选出其中规律, 从而对信号进行精细分析。与小波变换方法仅对信号低频数据分解不同, 小波包变换方法对信号高频数据也进行分解, 并根据被分析信号的特征自适应地选择相应频带, 使之与信号频谱相匹配, 从而提高时频分辨率。小波包变换在小波变换基础上提供更多可使用的正交基, 信号S的两层小波包分解流程如图 2所示。
|
Download:
|
| 图 2 信号S的两层小波包分解流程 Fig. 2 Two-layer wavelet packet decomposition flow of signal S | |
小波包分解的函数方程如式(2)[18]所示:
| $ W_{j,k}^n(t) = {2^{j/2}}{W^n}({2^j}t - k) $ | (2) |
其中, j为尺度指标(频域参数), k为位置指标(时间参数), 2j为分辨率, n=0, 1, …, N为振荡次数。
在使用小波包分析信号时, 通常选择n=0时函数φ(t)和ψ(t)作为正交尺度函数和小波函数进行分解和变换, 表达式如下:
| $ {W_{0,0}^0(t) = \varphi (t) = \sqrt 2 \sum\limits_k {{h_{0,k}}} \varphi (2t - k)} $ | (3) |
| $ {W_{0,0}^1(t) = \psi (t) = \sqrt 2 \sum \limits_k{{h_{1,k}}} \varphi (2t - k)} $ | (4) |
其中, h0, k和h1, k为滤波器系数。
当n=1, 2, …, N时, 对应的小波包函数为:
| $ {W_{0,0}^{2n}(t) = \sqrt 2 \sum\limits_k h (k)W_{1,k}^n(2t - k)} $ | (5) |
| $ {W_{0,0}^{2n + 1}(t) = \sqrt 2 \sum\limits_t g (k)W_{1,k}^n(2t - k)} $ | (6) |
由式(5)和式(6)确定的函数集合
假设信号用函数f(t)表示, 使用小波包对其进行分解, 用Pji(t)表示分解后第j层上第i个分解系数, G和H为小波分解滤波器, 则两层小波包分解的快速算法为:
| $ {P_0^1 = f(t)} $ | (7) |
| $ {P_j^{2i - 1} = \sum\limits_k H (k - 2t)P_{j - 1}^i(t)} $ | (8) |
| $ {P_j^{2i} = \sum\limits_k G (k - 2t)P_{j - 1}^i(t)} $ | (9) |
两层小波包分解的重构算法为:
| $ {P_j^i = 2\left[ {\sum\limits_k h (t - 2k)P_{j + 1}^{2i - 1}(t) + \sum\limits_k g (t - 2k)P_{j + 1}^{2i}(t)} \right]} $ | (10) |
其中, j=J-1, …, 1, 0;i=2j, …, 2, 1;J=lb N; h和g为小波重构滤波器。
1.3 奇异谱分析奇异谱分析方法是一种分析数据不同成分分布的方法, 主要应用于非线性数据。该方法先将数据在轨迹矩阵重构变换, 经奇异值分解(Singular Value Decomposition, SVD)[19]后将数据分组重构, 最终使用不同成分数据取代原始数据。与主成分分析(Principal Component Analysis, PCA)[12]不同的是, 由于奇异谱分析可以基于特殊的矩阵结构处理单次功耗数据, 因此其用于处理小波包分解低频部分和高频部分。
奇异谱分析包括分解和重构两部分[20]:
1) 分解。
假设待分析数据是长度为T的1维离散时间序列, 选择适当窗口宽度L(2≤L≤T), 将待分析数据YT=(y1, y2, …, yT)转化为多维轨迹矩阵X:
| $ \mathit{\boldsymbol{X}} = ({x_{ij}})_{i,j = 1}^{L,K} = \left( {\begin{array}{*{20}{c}} {{y_1}}&{{y_2}}& \cdots &{{y_K}}\\ {{y_2}}&{{y_3}}& \cdots &{{y_{K + 1}}}\\ \vdots & \vdots &{}& \vdots \\ {{y_L}}&{{y_{L + 1}}}& \cdots &{{y_T}} \end{array}} \right) $ | (11) |
其中, K=T-L+1, 窗口宽度L按照式(12)[21]选取最优值。
| $ L = \left\lfloor {{\rm{lg}}{{(T)}^c}} \right\rfloor ,c \in [1.5,3] $ | (12) |
计算XXT得到L个特征值λ1≥λ2≥…≥λL≥0, U1, U2, …, UL为相应的特征向量, 另外选取d=max(i, λi>0)=R(A), 将多维轨迹矩阵X分解如下:
| $ \mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{X}}_1} + {\mathit{\boldsymbol{X}}_2} + \cdots + {\mathit{\boldsymbol{X}}_d} $ | (13) |
其中,
2) 重构。
对式(13)中Xi进行变换生成相应时间序列, 得到的每组数据均表征原始数据某方面的特征。处理后的数据通常存于几个主要奇异值对应的时间序列中, 例如
| $ {\mathit{\boldsymbol{X}}_L} = \sum\limits_{i \in \mathit{\boldsymbol{M}}} {\sqrt {{\lambda _i}} } {\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{V}}_i^\prime \to \mathit{\boldsymbol{H}} \subset \{ {h_0},{h_1}, \cdots ,{h_{T - 1}}\} $ | (14) |
根据式(15)对XL矩阵求对角平均可计算得到H。
| $ {h_n} = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{n}\sum\limits_{K = 1}^{n + 1} {x_{k,n - k + 2}^*} ,0 \le n \le {L^*} - 1}\\ {\frac{1}{{{L^*}}}\sum\limits_{K = 1}^{L*} {x_{k,n - k + 2}^*} ,{L^*} - 1 \le n \le {K^*}}\\ {\frac{1}{{T - {n_K}}}\sum\limits_{n - {K^*} + 2}^{T - {K^*} + 1} {x_{k,n - k + 2}^*} ,{K^*} \le n \le T} \end{array}} \right. $ | (15) |
其中, x*为矩阵XL中的元素, 且:
| $ {{L^*} = {\rm{min}}\{ L,K\} } $ | (16) |
| $ {{K^*} = {\rm{max}}\{ L,K\} } $ | (17) |
在使用小波包变换方法降噪的过程中, 阈值选择和阈值量化方法与数据降噪效果紧密相关[22]。在实际应用中, 可选择默认阈值或者不断测试调整参数两种方式进行降噪。其中, 默认阈值的方式缺乏针对性, 无法根据功耗数据特点进行准确降噪。而在不断测试调整参数的方式中, 参数只适用于当前功耗数据降噪, 不具有普遍性。此外, 小波包变换方法只针对每层高频系数阈值进行降噪, 忽略低频系数中大量噪声[23], 从而降低功耗攻击效率与密钥破解准确率。
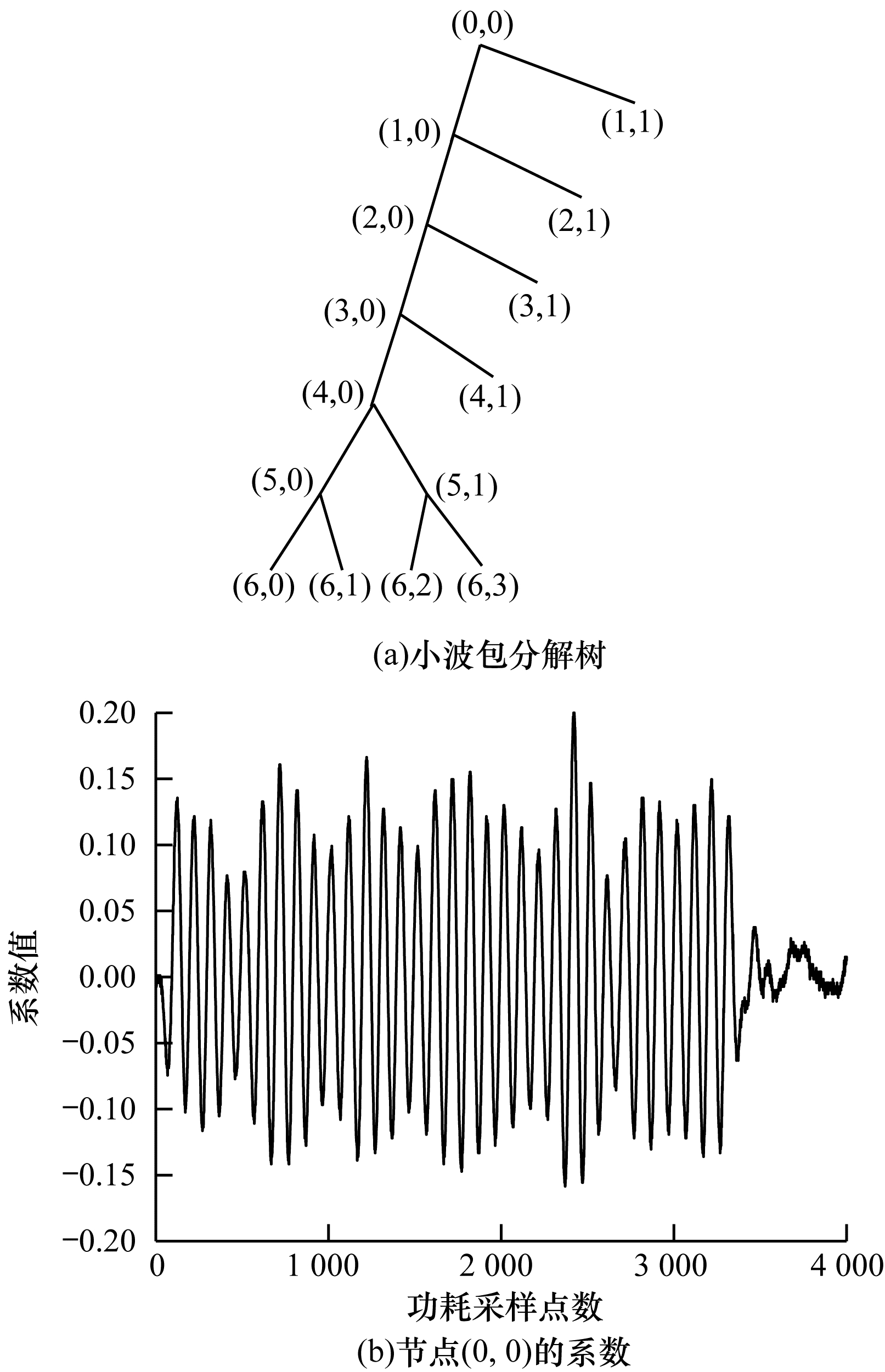
针对上述问题, 本文将奇异谱分析添加到小波包分解降噪过程中, 对功耗数据进行预处理以提高功耗攻击效率和密钥破解准确率。针对从实验室采集到的功耗数据, 使用小波包对每条功耗高频信息与低频信息逐层分解形成小波包分解树(本文选择使用sym6小波, 分解6层), 选择一个合适熵标准, 使用Matlab自带的小波包相关函数(besttree()函数计算小波包最佳树, 由leaves()函数获得小波包树所有节点, wpcoef()函数计算节点系数值)求解小波包分解的最佳小波包树, 如图 3所示。
|
Download:
|
| 图 3 最佳小波包分解树 Fig. 3 Optimal wavelet packet decomposition tree | |
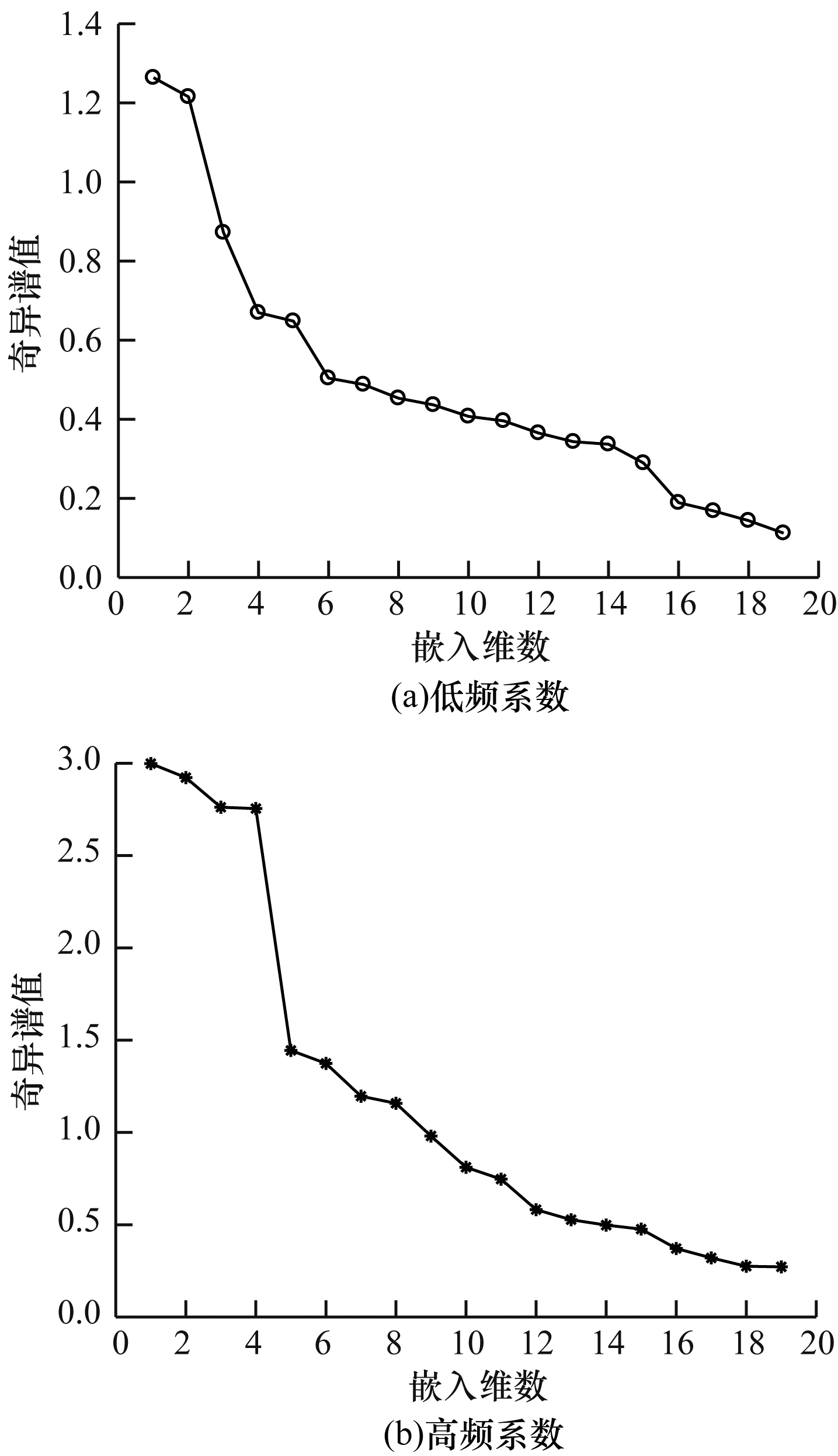
使用奇异谱分析计算小波包树各节点最佳奇异谱值。某节点分解后低频系数和高频系数的奇异谱值分布如图 4所示。而根据奇异熵定义:
| $ \begin{array}{*{20}{l}} {\Delta {E_i} = - \left( {{\lambda _i}\sum\limits_{j = 1}^i {{\lambda _j}} } \right){\rm{lb}}\left( {{\lambda _i}\sum\limits_{j = 1}^i {{\lambda _j}} } \right)}\\ {{E_k} = \sum\limits_{i = 1}^k \Delta {E_i}} \end{array} $ | (18) |
|
Download:
|
| 图 4 节点低频系数和高频系数奇异谱值分布 Fig. 4 Singular spectrum value distribution of low and high frequency coefficients of nodes | |
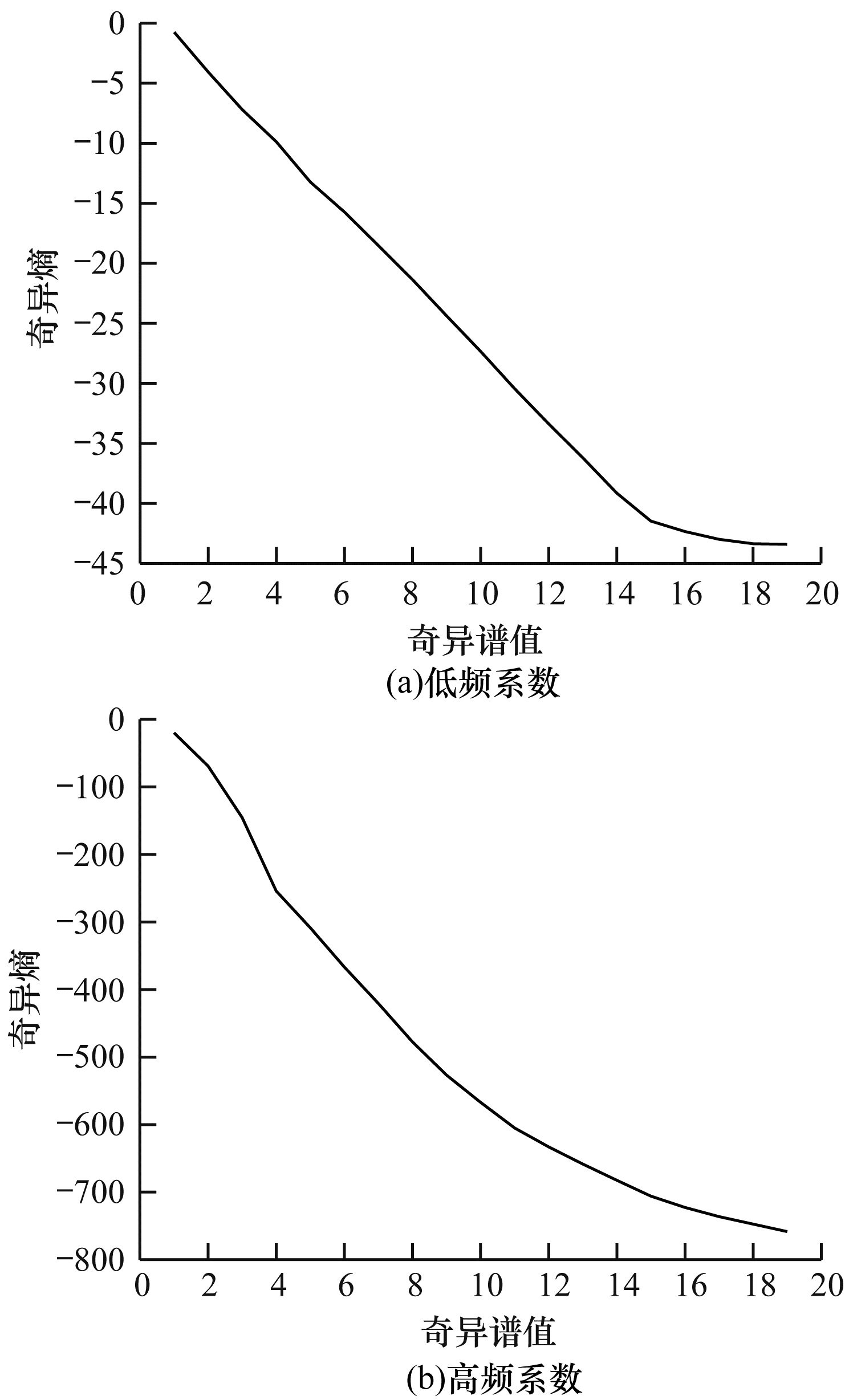
其中, λ为对应的奇异值, k为奇异熵阶次, ΔEi为奇异熵在阶次i处的增量, Ek为k阶对应的奇异熵。由式(18)计算得到各奇异值对应的奇异熵, 获得节点奇异熵分布, 如图 5所示。
|
Download:
|
| 图 5 节点低频系数和高频系数奇异熵分布 Fig. 5 Singular entropy distribution of low and high frequency coefficients of nodes | |
由图 5可以看出, 节点低频系数和高频系数奇异熵均随奇异值的增大而减小, 最终趋于平缓, 可认为处于平缓位置的奇异熵值所代表的节点信息为噪声含量。根据奇异熵分布趋势去除其中的噪声, 通过奇异谱分析重构去除噪声节点系数, 对处理后各节点进行小波包重构, 可得到预处理后的功耗数据。
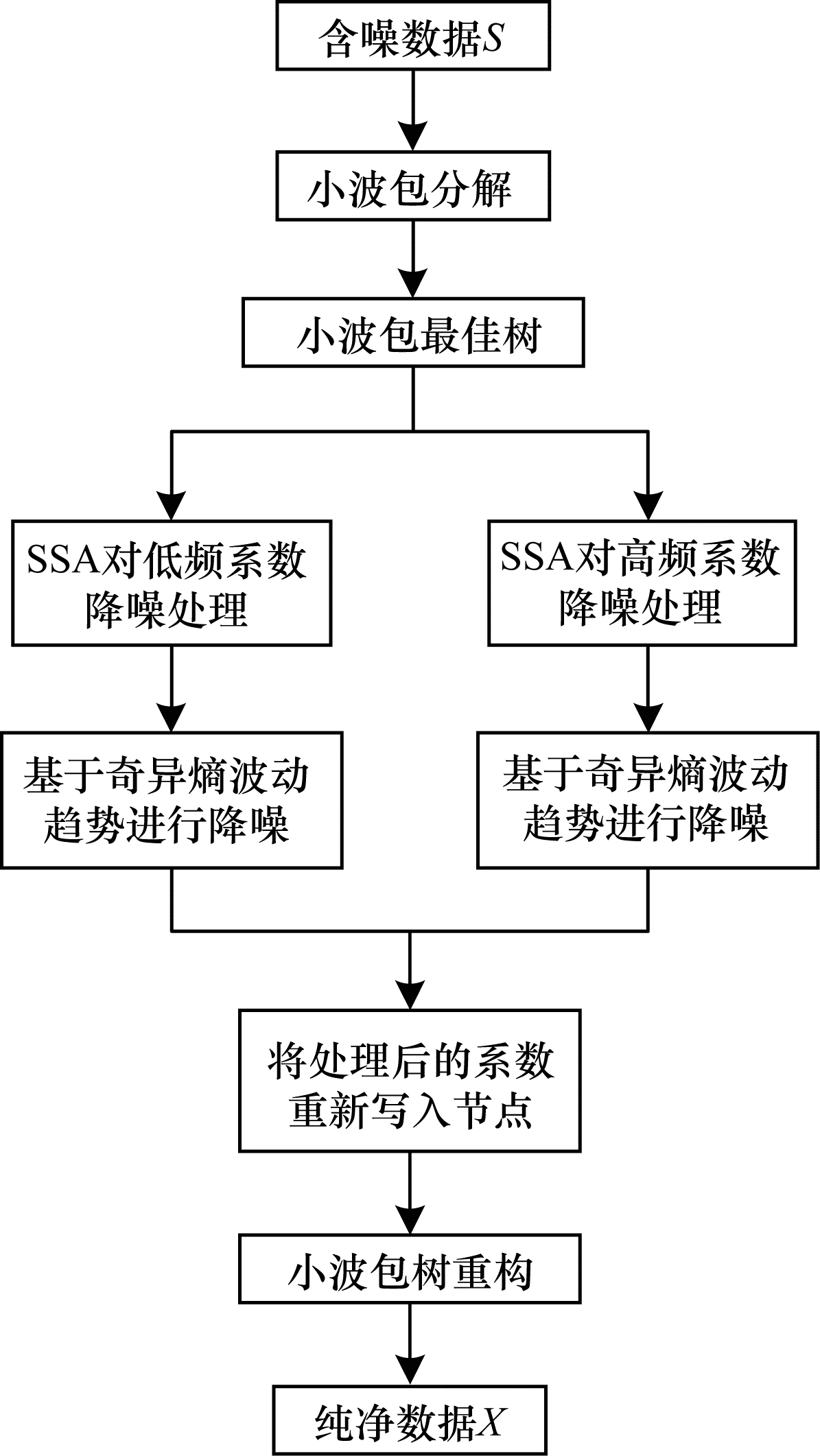
图 6为改进后的小波包降噪流程, 具体步骤为:
|
Download:
|
| 图 6 改进后小波包降噪流程 Fig. 6 Denoising flow of improved wavelet packet | |
1) 利用小波包分解功耗数据。先挑选一个对称性、紧支撑性和正交性较好的小波作为小波包分解的小波基, 再确定小波包分解层数。
2) 获得最佳小波包树。
3) 使用奇异谱分析奇异熵分布趋势, 对小波包分解系数进行降噪处理。
4) 小波包重构。将上述步骤中处理的节点系数重新写入小波包树节点, 通过小波包重构得到降噪后的功耗数据。
3 实验与结果分析为评估本文方法对相关功耗攻击效率和密钥破解准确率的提升效果, 选择基于硬件的SM4算法进行选择明文攻击。通过SM4对特定明文进行加密, 选择第1轮4个S盒作为泄漏点采集功耗数据, 其中采集的1条功耗数据如图 7所示, 采样速率为5 Gp/s。使用原始功耗数据、改进前小波包降噪功耗数据和改进后小波包降噪功耗数据进行相关功耗攻击, 分析不同功耗数据对应的攻击效率和密钥破解准确率。
|
Download:
|
| 图 7 功耗数据 Fig. 7 Power consumption data | |
在相关功耗攻击中, 相关系数是衡量去噪方法性能的重要指标。使用原始功耗数据与经过预处理的功耗数据进行相关功耗攻击, 通过比较正确密钥攻击结果的相关系数大小可确定去噪性能高低。图 8为使用原始功耗数据、改进前小波包降噪功耗数据和改进后小波包降噪功耗数据的相关功耗攻击对比结果, 可见正确密钥(242)对应的相关系数均最大, 表示3种功耗数据都能确保相关功耗攻击成功破解密钥。在原始功耗数据与改进前小波包降噪功耗数据下相关功耗攻击中, 出现与正确密钥相关系数0.192 9、0.191 2对应峰形较接近的尖峰, 通常被称为“鬼峰”。鬼峰会对相关功耗攻击结果造成干扰, 导致功耗曲线条数增加。而使用改进后小波包降噪功耗数据在相关功耗攻击下, 其鬼峰与正确密钥相关系数对应峰形距离较大, 对相关功耗攻击结果干扰较小, 相关功耗攻击结果可靠性得到提高。此外, 原始功耗曲线、改进前小波包降噪功耗曲线和改进后小波包降噪功耗曲线对应的最大相关系数分别为0.194 5、0.242 1和0.412 7。由相关功耗攻击原理可知, 最大相关系数值越大则越易区分出正确密钥对应的功耗, 因此, 使用改进后小波包降噪功耗数据的相关功耗攻击性能较原始功耗数据和小波包降噪功耗数据分别提升了53%与41%。

|
Download:
|
| 图 8 3种数据相关功耗攻击结果对比 Fig. 8 Comparison of three kinds of data related power attack results | |
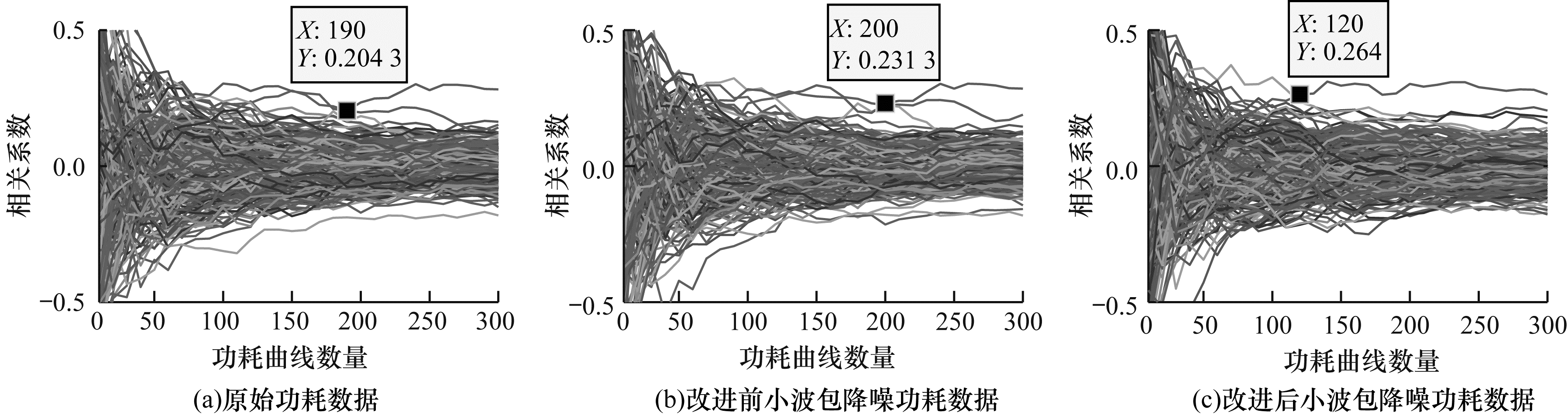
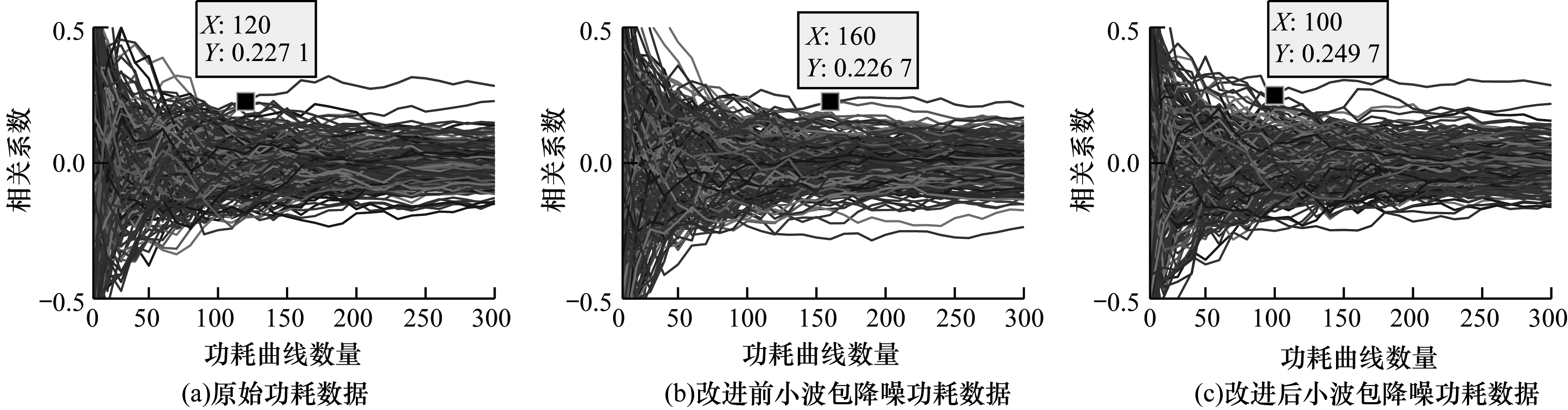
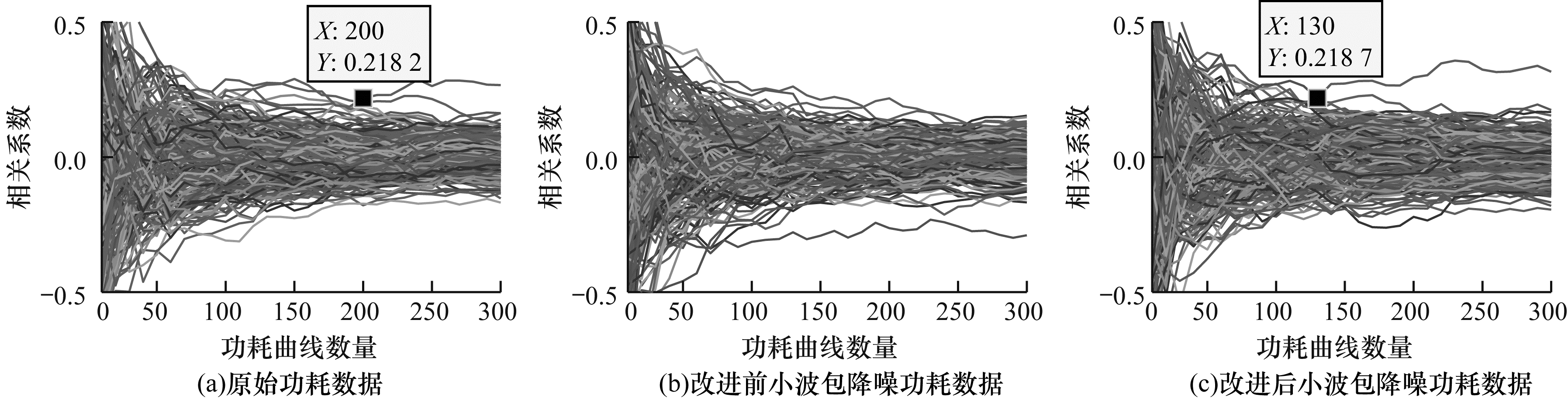
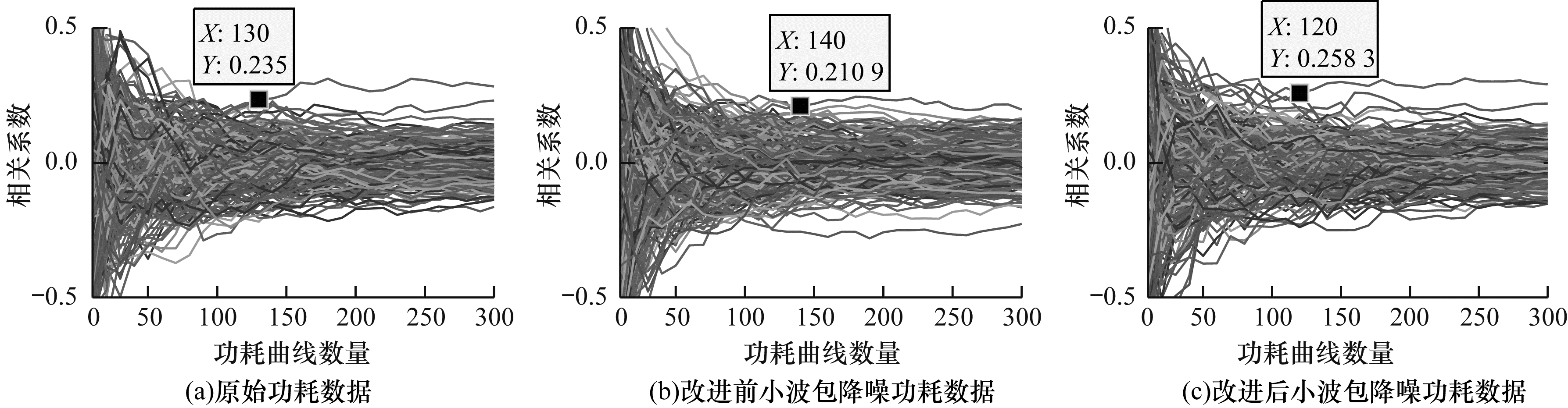
图 9~图 12分别为使用原始功耗数据、改进前小波包降噪功耗数据和改进后小波包降噪功耗数据对4个S盒进行相关功耗攻击, 得到相关系数与功耗曲线数量之间的关系。可以看出:当原始功耗曲线数量分别为190条、120条、200条和130条时成功破解密钥(此时正确密钥与错误密钥的相关系数开始分离且后续不再重合); 使用改进前小波包降噪对数据处理后, 在破解密钥上会导致功耗曲线数量增长, 无法正确破解第3个S盒的密钥; 使用改进后小波包降噪对数据处理后, 在破解密钥上功耗曲线数量会出现不同程度地减少, 破解4个S盒密钥分别需要120条、100条、130条和120条功耗曲线, 其攻击效率较使用原始功耗数据分别提高37%、17%、35%和8%。
|
Download:
|
| 图 9 第1个S盒功耗曲线数量与相关系数的关系 Fig. 9 Relationship between the number of power consumption curves of the first S-box and correlation coefficient | |
|
Download:
|
| 图 10 第2个S盒功耗曲线数量与相关系数的关系 Fig. 10 Relationship between the number of power consumption curves of the second S-box and correlation coefficient | |
|
Download:
|
| 图 11 第3个S盒功耗曲线数量与相关系数的关系 Fig. 11 Relationship between the number of power consumption curves of the third S-box and correlation coefficient | |
|
Download:
|
| 图 12 第4个S盒功耗曲线数量与相关系数的关系 Fig. 12 Relationship between the number of power consumption curves of the fourth S-box and correlation coefficient | |
本文将奇异谱分析与小波包降噪相结合, 提出一种基于改进小波包分解的相关功耗攻击降噪方法。使用小波包分解求出最优小波包树, 提取各节点中功耗数据的低频系数及高频系数, 运用奇异谱分析并根据各奇异熵分布趋势去除节点系数的噪声信息, 并将处理后的节点系数写入小波包树, 通过数据重构获得降噪后的功耗数据。对SM4算法进行选择明文的相关功耗攻击实验表明, 该方法能有效解决小波包分解中功耗数据预处理缺乏针对性的问题, 保留高频功耗数据信息并提高功耗质量, 较改进前小波包降噪方法的攻击效率更高。虽然本文方法在攻击性能和效率上有所提升, 但其本质是将功耗数据作为信号数据来进行预处理降噪, 并未考虑功耗数据本身特征, 导致降噪效果和攻击效率不稳定。后续将分析功耗数据特征并提出更具针对性的功耗数据预处理方法, 以进一步提升相关功耗攻击性能和效率。
| [1] |
KOCHER P C, JAFFE J M, JUN B C.Differential power analysis: US0059826[P]. 2009-12-15.
|
| [2] |
KOCHER P C.Timing attacks on implementations of Diffie-Hellman, RSA, DSS, and other systems[C]//Proceedings of CRYPTO'96.Berlin, Germany: Springer, 1996: 104-113.
|
| [3] |
AGRAWAL D, ARCHAMBEAULT B, RAO J R, et al.The EM side-channel(s): attacks and assessment methodologies[EB/OL].[2019-06-08]. https://www.researchgate.net/publication/253323767_The_EM_Side-ChannelsAttacks_and_Assessment_Methodologies.
|
| [4] |
BRIER E, CLAVIER C, OLIVIER F.Correlation power analysis with a leakage model[C]//Proceedings of International Workshop on Cryptographic Hardware and Embedded Systems.Berlin, Germany: Springer, 2004: 16-29.
|
| [5] |
LE T H, CLEDIERE J, SERVIERE C, et al. Noise reduction in side channel attack using fourth-order cumulant[J]. IEEE Transactions on Information Forensics and Security, 2007, 2(4): 710-720. DOI:10.1109/TIFS.2007.910252 |
| [6] |
CHARVET X, PELLETIER H.Improving the DPA attack using wavelet transform[EB/OL].[2019-06-08]. https://www.researchgate.net/publication/228717434_Improving_the_DPA_attack_using_Wavelet_transform.
|
| [7] |
SOUISSI Y, ABDELAZIZ M, AABID E, et al.Novel applications of wavelet transforms based side-channel analysis[EB/OL].[2019-06-08]. https://www.researchgate.net/publication/265359018_Novel_Applications_of_Wavelet_Transforms_based_Side-Channel_Analysis.
|
| [8] |
LIU Wei, WU Liji, ZHANG Xiangmin, et al.Wavelet-based noise reduction in power analysis attack[C]//Proceedings of the 10th International Conference on Computational Intelligence and Security.Washington D.C., USA: IEEE Press, 2014: 405-409.
|
| [9] |
PENG Yanni. Application of wavelet transform to de-noising method[J]. Journal of Chongqing University(Natural Science Edition), 2004, 27(10): 40-43. (in Chinese) 彭燕妮. 小波变换在信号消噪中的应用[J]. 重庆大学学报(自然科学版), 2004, 27(10): 40-43. |
| [10] |
DUAN Xiaoyi, SHE Gaojian, GAO Xianwei, et al. Correlation power analysis attack for AES based on wavelet packet[J]. Computer Engineering, 2017, 43(6): 84-91. (in Chinese) 段晓毅, 佘高健, 高献伟, 等. 基于小波包的AES相关功耗分析攻击[J]. 计算机工程, 2017, 43(6): 84-91. DOI:10.3969/j.issn.1000-3428.2017.06.014 |
| [11] |
JAMES B E, ANASTASIOS A T.Singular spectrum analysis[EB/OL].[2019-06-08]. https://link.springer.com/book/10.1007%2F978-1-4757-2514-8.
|
| [12] |
WOLD S, ESBENSEN K, GELADI P. Principal component analysis[J]. Chemometrics and Intelligent Laboratory Systems, 1987, 2(1): 37-52. |
| [13] |
YANG Wenxian, JIANG Jiesheng. Study on the singular entropy of mechanical signal[J]. Journal of Mechanical Engineering, 2000, 36(12): 9-13. (in Chinese) 杨文献, 姜节胜. 机械信号奇异熵研究[J]. 机械工程学报, 2000, 36(12): 9-13. DOI:10.3321/j.issn:0577-6686.2000.12.003 |
| [14] |
TENG Yongping, CHEN Yun, CHEN Jun, et al. Research on DPA and CPA for SM4 algorithm[J]. Journal of Chengdu University of Information Technology, 2014, 29(1): 13-18. (in Chinese) 滕永平, 陈运, 陈俊, 等. SM4算法的差分功耗以及相关功耗分析研究[J]. 成都信息工程学院学报, 2014, 29(1): 13-18. DOI:10.3969/j.issn.1671-1742.2014.01.002 |
| [15] |
PAN Mingzhong, LÜ Xinhua, ZHANG Libo, et al. Signal analysis based on a synthetic method of wavelet transform and fourier transform[J]. China Information Security, 2007, 5(6): 62-63. (in Chinese) 潘明忠, 吕新华, 张立波, 等. 小波变换与傅立叶变换相结合的信号实例分析[J]. 信息安全与通信保密, 2007, 5(6): 62-63. DOI:10.3969/j.issn.1009-8054.2007.06.034 |
| [16] |
LIU Zhisong. Signal de-noising based on the wavelet transform[J]. Journal of Zhejiang Ocean University(Natural Science Edition), 2011, 30(2): 150-154. (in Chinese) 刘志松. 基于小波分析的信号去噪方法[J]. 浙江海洋学院学报(自然科学版), 2011, 30(2): 150-154. DOI:10.3969/j.issn.1008-830X.2011.02.012 |
| [17] |
QI Xianghui.Study of quantization selection strategy based on wavelet packet transform[D]. Xi'an: Northwest University, 2018.(in Chinese) 齐祥会.基于小波包变换的量化择时策略的研究[D].西安: 西北大学, 2018. |
| [18] |
NIKOLAOU N G, ANTONIADIS I A. Rolling element bearing fault diagnosis using wavelet packets[J]. NDT and E International, 2002, 35(3): 197-205. DOI:10.1016/S0963-8695(01)00044-5 |
| [19] |
GOLUB G H, NREINSCH C. Singular value decomposition and least squares solutions[J]. Numerische Mathematik, 1971, 14: 403-420. |
| [20] |
AI Juan, WANG Zhu, ZHOU Xinping, et al.Improved wavelet transform for noise reduction in power analysis attacks[C]//Proceedings of IEEE International Conference on Signal and Image Processing.Washington D.C., USA: IEEE Press, 2016: 602-606.
|
| [21] |
KHAN M A R, POSKITT D S.Window length selection and signal-noise separation and reconstruction in singular spectrum analysis[EB/OL].[2019-06-08]. https://www.researchgate.net/publication/254431163_Window_Length_Selection_and_Signal-Noise_Separation_and_Reconstruction_in_Singular_Spectrum_Analysis.
|
| [22] |
LÜ Nannan, SU Shujing, ZHAI Chengrui. Application of improved wavelet packet threshold algorithm tn vibration signal denoising[J]. Journal of Detection and Control, 2018, 40(1): 119-124. (in Chinese) 吕楠楠, 苏淑靖, 翟成瑞. 改进小波包阈值算法在振动信号去噪中的应用[J]. 探测与控制学报, 2018, 40(1): 119-124. |
| [23] |
WU Huijuan, CAO Hui.Application of wavelet packet de-noising signal processing in thunder[EB/OL].[2019-06-08]. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CPFD&filename=OGSM201510001095.(in Chinese) 武慧娟, 曹辉.小波包降噪在雷声信号处理中的应用[EB/OL].[2019-06-08]. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CPFD&filename=OGSM201510001095. |
 2020, Vol. 46
2020, Vol. 46

 ,
,