开放科学（资源服务）标志码（OSID）：

0 概述

时间敏感网络（Time-Sensitive Network，TSN）是一种新型的数据确定性传输网络，在以太网的基础上加入了时间同步、传输调度、路径控制、资源预留、可靠冗余等新机制，使得时间关键或任务关键应用的服务质量（Quality of Service，QoS）得到保证^[1]。TSN支持时间敏感流量和尽力而为（Best Effort，BE）流量在同一网络中进行传输，并对前者提供低延迟、低抖动和低丢包率^[2]服务。由于TSN能够将以太网的低成本、高带宽特点与高质量的数据传输相结合，因此TSN相关技术已经得到了学术界和产业界的广泛关注^[3-5]。尽管TSN具有以上优点，但是在实际的分析和计算中，由于网络结构众多、数据流QoS各异，因此会导致TSN系统的调度计算呈现出复杂性。已有众多研究表明，TSN中的流量调度问题是NP完全问题^[6-8]。低效率、拓展性差的调度计算方法将会导致计算时间消耗大、计算颗粒度粗等问题，不利于TSN系统的快速、高质量部署。

众多学者针对上述问题进行了大量研究。ARESTOVA等^[7]综合考虑了网络设备、TSN流的属性和不同路由方式带来的影响，设计一种基于混合遗传算法的计算方法，并对调度结果进行压缩。PAHLEVAN等^[9]同时考虑路由约束和调度约束，采用启发式列表调度方法提高计算性能，并对分布式系统、多播流和流关系进行讨论。GAVRILUT等^[10]在计算中增加了对AVB流量的考虑，利用GRASP算法同时进行路由和调度计算，使得系统中的时间敏感流量和AVB流量都能满足传输需求。DURR等^[11]针对计算粒度粗、带宽浪费等问题，将调度问题映射到经典JSP问题，利用禁忌搜索进行调度计算，并通过调度压缩节省带宽。总体而言，上述各项研究均从不同角度完成了对TSN网络的路由和调度计算，但也存在路由调度分离、计算效率低、颗粒度粗等问题，在计算速度和优化效果上有待提升。

本文从高效率流量路由调度计算的角度出发，提出一种基于最短路径负载均衡和改进遗传算法的流量调度方法。在路由计算部分，考虑到流与流在传输过程中的相互影响，利用链路负载均衡的思想进行规划。在调度计算部分，使用优势个体保留的选择算子和自适应交叉变异概率，对遗传算法进行改进，防止过早收敛和陷入局部极值，以充分提升算法的搜索效率。

1 问题建模 1.1 网络模型与流量模型

在TSN网络模型中包含终端、交换机、传输链路这3种要素，其中终端和交换机合称为节点。各个节点均是支持TSN特性的设备，传输链路是全双工的以太网链路。将网络属性归结为关于拓扑$ \tau $和节点数量$ n $的二元组，如式（1）所示：

$ {P}_{\mathrm{N}}=\{\tau , n\} $

(1)

对于特定拓扑的网络而言，可以将其表示为有向图，如式（2）所示：

$ G=\{V, E\} $

(2)

其中：$ {v}_{i}\in V $表示节点，包含终端和交换机；$ ({v}_{a}, {v}_{b}), $ $ ({v}_{b}, {v}_{a})\in E $表示节点之间双向链路的集合。

将从源节点开始且按照一定要求传输到目的节点的有序数据序列称为流，并将所有时间敏感流的集合记为$ F $。对于每种不同的流，其主要参数包含流的传输路径$ R $、流的传输周期$ T $、流的负载值$ P $、流的端到端时间限制$ D $。例如，对于流$ {f}_{i} $，可用以下四元组表示：

$ {f}_{i}=({R}_{i}, {T}_{i}, {P}_{i}, {D}_{i}) $

(3)

不同的流可能通过不同的路径进行传输，对于源节点是$ {v}_{\mathrm{s}\mathrm{r}\mathrm{c}} $、目的节点是$ {v}_{\mathrm{d}\mathrm{s}\mathrm{t}} $且中间经过$ {v}_{1}, {v}_{2}, \cdots , {v}_{n} $共$ n $个节点的流，可将其路径表示为$ {R}_{i}=\left\{{v}_{\mathrm{s}\mathrm{r}\mathrm{c}}, {v}_{1}, \right. $ $ \left.{v}_{2}, \cdots , {v}_{n}, {v}_{\mathrm{d}\mathrm{s}\mathrm{t}}\right\} $。流负载的单位是字节，每个帧的最大长度为以太网的最大传输单元（Maximum Transmission Unit，MTU）。每个时间敏感流都有端到端的时间限制，即目的节点处的接收时间与源节点处的发送时间之差应在规定范围内，用$ {D}_{i} $表示。

1.2 TSN传输约束

在TSN网络中，为了确保时间敏感的数据流量能够及时准确送达，需要对网络传输行为施加一定的约束。本文的研究目标是求出在满足这些约束条件下的可行解，并去寻求最优解或近似最优解，同时尽量提高计算效率和可扩展性。路由问题的核心是在减小链路负载和拥塞的情况下，求解不同流的传输路径。调度问题的核心可以归结为计算每条链路上传输时间窗的开窗时间与关窗时间。在TSN中，共有5种传输约束^[12-14]。

约束1  对于任一条链路上的时间窗而言，其开窗时间不应超过其关窗时间，如式（4）所示：

$ {f}_{i, m}^{e}.{t}_{\mathrm{s}}\le {f}_{i, m}^{e}.{t}_{\mathrm{e}} $

(4)

其中：$ {f}_{i, m}^{e} $表示流$ {f}_{i} $在链路e上的第m帧；$ {t}_{\mathrm{s}} $表示开窗时间；$ {t}_{\mathrm{e}} $表示关窗时间。

约束2  对于同一条链路，应当满足首帧的发送时间为非负，且各帧按照先后顺序进行发送，如式（5）、式（6）所示：

$ {f}_{i, 0}^{e}.{t}_{\mathrm{s}}\ge 0 $

(5)

$ {f}_{i, k+1}^{e}.{t}_{\mathrm{s}}-{f}_{i, k}^{e}.{t}_{\mathrm{e}}\ge 0 $

(6)

约束3  在同一段传输时隙内，链路资源应当是被当前流所独占的，不同的流之间不会发生碰撞，如式（7）、式（8）所示：

$ {f}_{i, m}^{e}.{t}_{\mathrm{s}}+A\cdot {T}_{i}\ge {f}_{j, n}^{e}.{t}_{\mathrm{e}}+B\cdot {T}_{j} $

(7)

$ {f}_{j, n}^{e}.{t}_{\mathrm{s}}+B\cdot {T}_{j}\ge {f}_{i, m}^{e}.{t}_{\mathrm{e}}+A\cdot {T}_{i} $

(8)

其中：$ m\ne n $；$ A, B\in {\mathbb{N}}^{\mathrm{*}} $；$ {T}_{i} $、$ {T}_{j} $表示对应流的周期。

约束4  同一数据流在不同链路上的传输是有先后顺序的，如式（9）所示：

$ {f}_{i, m}^{a}.{t}_{\mathrm{e}}\le {f}_{i, m}^{b}.{t}_{\mathrm{s}} $

(9)

其中：$ \forall a, b\in \mathbb{E} $，且在路由中$ a $位于$ b $前面。

约束5  流的端到端时延不应超出最大限制，如式（10）所示：

$ {f}_{i, \mathrm{l}\mathrm{a}\mathrm{s}\mathrm{t}}^{\mathrm{e}\mathrm{n}\mathrm{d}}.{t}_{\mathrm{e}}-{f}_{i, 0}^{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}.{t}_{\mathrm{s}}\le {D}_{i} $

(10)

2 基于最短路径负载均衡与MGA的流量调度 2.1 基于K最短路径的负载均衡路由算法

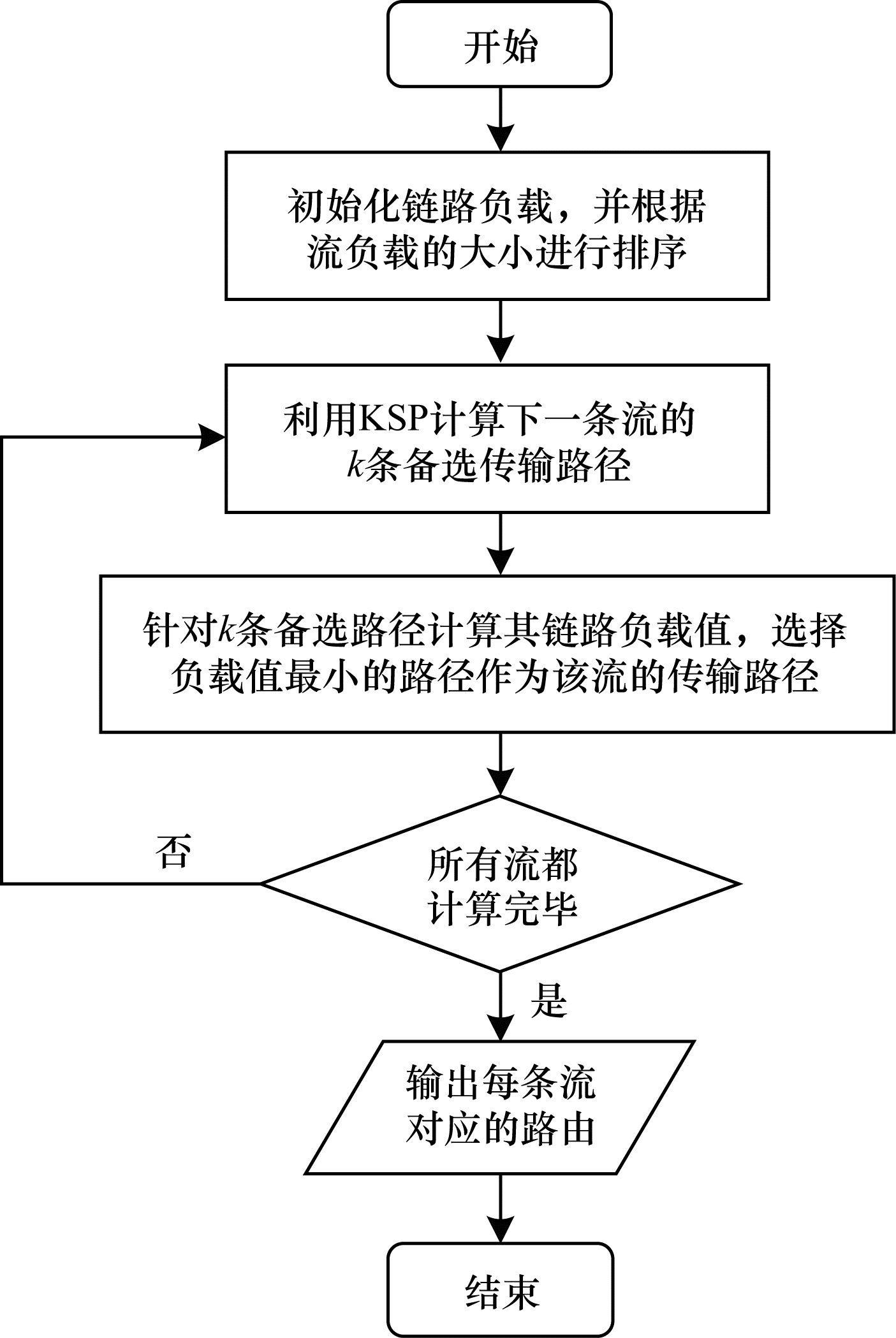
根据IEEE Std 802.1Qca-2015^[15]，传统TSN系统中采用带有约束的最短路径优先（Constrained Shortest Path First，CSPF）路由。如果同源节点和目的节点之间同时有多条最短路径路由，那么会根据一定的约束条件进行剪枝。然而文献[16]研究表明，采用最短路径算法（Shortest Path Algorithm，SPA）有可能产生额外的延迟。数据的路由不仅需要减少转发操作，而且要使其路由通过有较少数据重叠的路径。当每种数据流仅按照自身的最短路径进行路由而不考虑流与流之间的相互影响时，虽然自身可能是最优解，但是也可能会导致整体时延的增加。因此，本文提出一种基于K最短路径的负载均衡路由算法（Load Balancing Routing Algorithm based on K Shortest Path，LBRA-KSP）。该算法能够针对不同的数据流寻找路由，使得链路负载达到最小。LBRA-KSP算法流程如图 1所示。

LBRA-KSP算法的输入为网络拓扑、数据流及其属性，输出为每条流所对应的路由路径，主要步骤如下：

1）数据的初始化。对于输入的拓扑结构，将图中各条链路的初始负载值设置为0。对于输入的流，LBRA-KSP算法主要考虑其源地址、目的地址和流负载这3种属性，并将所有的输入流按照流负载从小到大进行排序。

2）计算备选路径。LBRA-KSP算法综合考虑路径长度和流之间的相互作用，以此来获得更优质的传输路径。对于某条流，采用KSP算法，计算从源节点到目的节点的前K条最小距离路由。

3）路由选优。路由选优是LBRA-KSP算法的关键，对于计算所得到的K条路由路径，计算每条备选路径的负载值，将新的负载值更新为历史负载值和新添加负载值之和，然后选择其中总负载值最小的那条路径作为该流的传输路径。

算法1  路由选优算法

输入  所有输入流的K条备选路径集合paths[]

输出  所有输入流的负载均衡路由集合route_all[]

1.for path in paths[]：

2.for i in range（0，K）：

3.for n in range（len（path）-1）：

4.获取payload_last

5.获取payload_now

6.payload = payload_last + payload_now

7.将payload加入payload_comp[]

8.payload = 0

9.选择payload_comp[]中最小的payload所对应的路径route

10.将route加入route_all[]

11.更新route所在路径的payload值

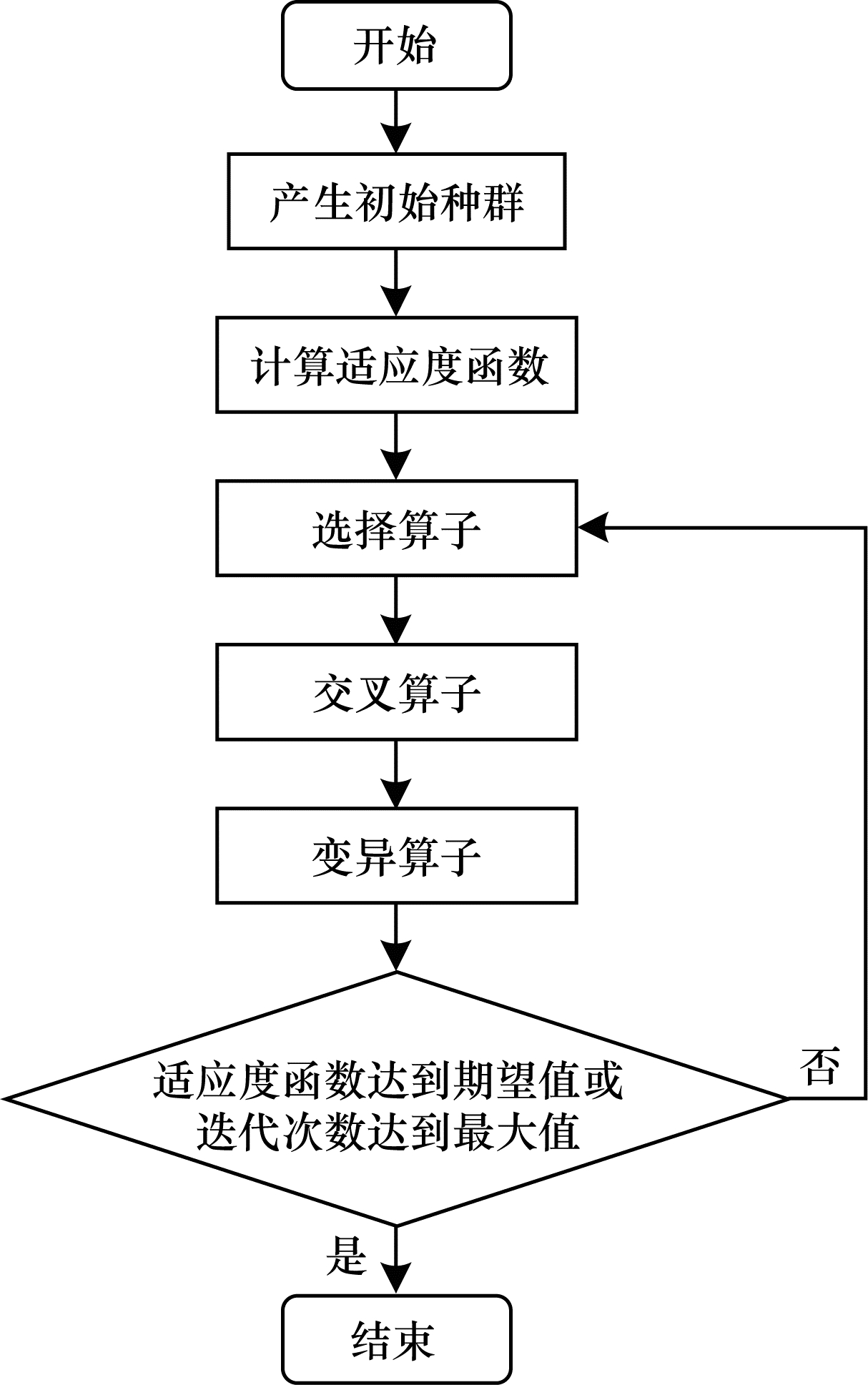
2.2 MGA算法

遗传算法借助生物界中的优胜劣汰思想和基因遗传原理，通过对自然种群繁衍进化的模拟来求得优化过程中的最优解。但是，遗传算法通常存在搜索效率较低、过早收敛、容易陷入局部极值等问题，JIA等^[17]针对上述问题进行优化形成改进的遗传算法（Modified Genetic Algorithm，MGA）。本文对MGA的选择算子和交叉变异概率进行改进，并结合LBRA-KSP的结果进行计算，全面提升了MGA的运行效果，如图 2所示。为便于计算，本文采取与文献[11]相同的假设，即各流的传输周期保持相同。

2.2.1 路径矩阵与时间矩阵

路径矩阵用于表示每条待调度的流所经过的各段链路，如式（11）所示：

$ {{\boldsymbol{r}}_{\text{route}}}=\left[\begin{array}{ccccc}1& 2& 3& 0& 0\\ 4& 5& 6& 0& 0\\ 7& 8& 9& 10& 0\\ 11& 4& 12& 13& 9\\ 5& 4& 14& 0& 0\\ 5& 6& 0& 0& 0\\ 8& 9& 0& 0& 0\end{array}\right] $

(11)

在路径矩阵中，行表示流的数量，列表示流的传输路径，行与列的下标均从0开始计数。例如，流3表示其传输路径经过链路11、链路4、……、链路9。相同的链路用同一种数字表示，不同的链路用不同的数字表示。例如，流1所经过的第0个传输链路与流3所经过的第1个传输链路、流4所经过的第1个传输链路是相同的。为了防止链路冲突的发生，需要进一步的调度计算。

时间矩阵表示数据流在每条链路上传输所消耗的时间，如式（12）所示：

$ {{\boldsymbol{t}}_{\text{time}}}=\left[\begin{array}{ccccc}{t}_{00}& {t}_{01}& {t}_{02}& 0& 0\\ {t}_{10}& {t}_{11}& {t}_{12}& 0& 0\\ {t}_{20}& {t}_{21}& {t}_{22}& {t}_{23}& 0\\ {t}_{30}& {t}_{31}& {t}_{32}& {t}_{33}& {t}_{34}\\ {t}_{40}& {t}_{41}& {t}_{42}& 0& 0\\ {t}_{50}& {t}_{51}& 0& 0& 0\\ {t}_{60}& {t}_{61}& 0& 0& 0\end{array}\right] $

(12)

时间矩阵$ {{\boldsymbol{t}}_{\text{time}}} $与路径矩阵$ {{\boldsymbol{r}}_{\text{route}}} $一一对应，在每条传输路径上可以根据负载值计算出相对应的数据传输用时。

2.2.2 适应度函数

时间敏感网络的核心为关键流量的确定性传输，并且对于每一条时间敏感的流，其端到端的传输时间不能够超过其最大时限。从整体而言，整个网络的流量调度总时间也要尽量短，使得整体GCL调度表尽量紧凑。因此，在调度计算时，不但需要满足每条流的时限，而且需要总任务的完成时间尽可能短。将适应度函数定义为：若某条染色体未能在时限内完成调度，则规定其适应度为-1，在之后的计算中将直接被淘汰，而其余在时限内的染色体适应度值设置为最大关窗时间减去最小开窗时间，如式（13）所示：

$ f=\left\{\begin{array}{l}\mathrm{m}\mathrm{a}\mathrm{x}({f}_{i}.{t}_{\mathrm{e}})-\mathrm{m}\mathrm{i}\mathrm{n}({f}_{i}.{t}_{\mathrm{s}}), {D}_{i}\ge {L}_{i}\\ -1, {D}_{i}<{L}_{i}\end{array}\right. $

(13)

算法2  适应度计算算法

输入  个体的染色体indiviaual

输出  对应的适应度值f

1.def fitness（individual）：

2.初始化left[]

3.初始化right[]

4.for indi_id，indi_value in individual

5.计算index_of_indi_value

6.flag_index = index_of_indi_value.index（indi_id）

7.flow = indi_value

8.link = route_matrix[indi_value][flag_index]

9.time = time_matrix[indi_value][flag_index]

10.right1 = max_right_before（）

11.right2 = right_available（）

12.for i in range（len（left[link]））：

13.if left[link][i]为空

14.left[link][i] =（flow，max（right1，right2））

15.right[link][i] =（flow，max（right1，right2）+ time）

16.makespan = max（right）

17.初始化latency

18.初始化left_temp right_temp

19.for fl in range（len（flow））：

20.将fl的所有left值添加至left_temp

21.将fl的所有right值添加至right_temp

22.latency = max（right_temp）–min（left_temp）

23.复位left_ temp right_temp

24.if latency > deadline：

25.f =-1

26.else：

27.f = makespan

28.return f

2.2.3 基于优势个体保留的选择算子

轮盘赌是遗传算法中最常见的选择算子，轮盘赌选择算子的基本思想为：个体选中的概率与其适应度函数的函数值成正比，以便能够尽可能多地复制种群中的优秀个体。假设群体的大小为$ n $，个体$ i $的适应度为$ {F}_{i} $，则个体$ i $被选中遗传到下一代群体的概率如式（14）所示：

$ {{P}_{i}}=\frac{{{F}_{i}}}{\sum\limits_{i=1}^{n}{{{F}_{i}}}} $

(14)

然而，在遗传算法的实际运行过程中，当迭代处于初始阶段时，轮盘赌选择算子会选择较多的高适应度个体，这些高适应度个体经过复制所得到的子代数目也会相应增加，导致整体种群丧失了多样性。当迭代处于末尾时期时，种群个体之间的差异已很小，适应度非常接近，此时再采用轮盘赌策略意义不大，于是本文使用优势个体保留的思想对其进行改进，具体步骤为：

步骤1  对种群进行适应度排序，按照适应度从高到低的顺序分成优秀个体、一般个体和较差个体这3个分区。

步骤2  淘汰所有较差个体分区内的染色体，并用优秀个体中的染色体进行替代。

步骤3  对步骤2中的种群进行交叉和变异操作得到新的子代，再将该种群按照步骤1~步骤3的顺序进行操作，以此类推，直到生成最终结果。

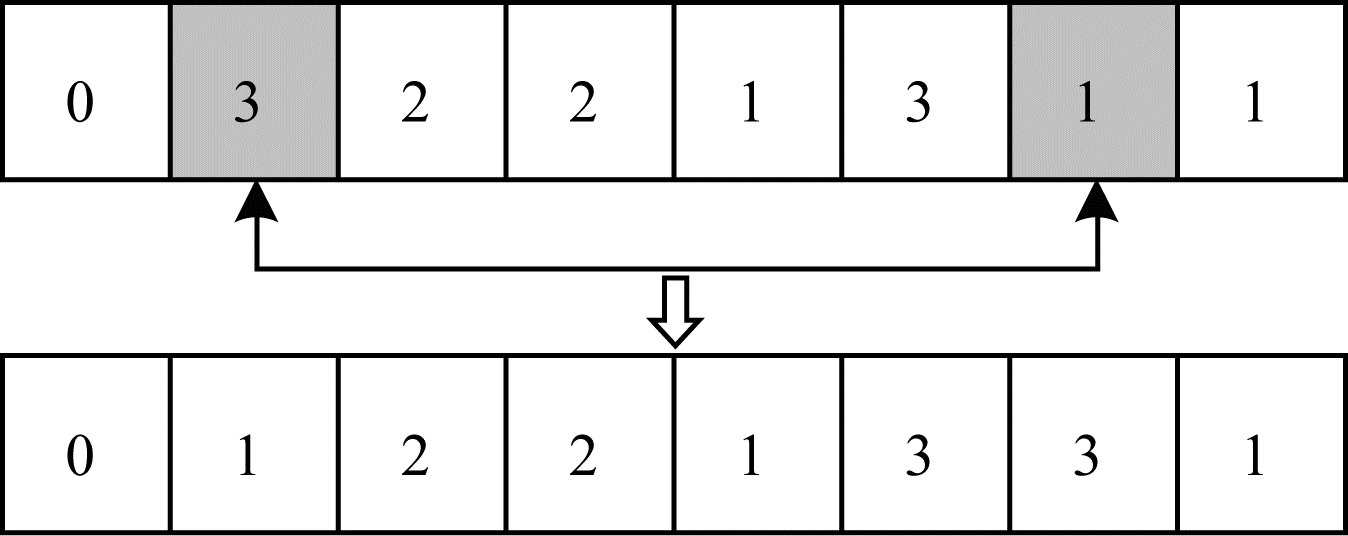
2.2.4 自适应交叉和变异算子

交叉算子采用顺序交叉（Order Crossover，OX）算子，基本操作过程为：首先选择一对用于交换的父代染色体，并且随机选择用于交换的基因片段；然后根据切割点，生成新的子代，并且保证切割区域内的内容不变；最后按照顺序依次将另一个父代中的其他基因填入子代中的空白区域。交叉算子的操作过程如图 3所示。变异算子采用位置变异算子，对于某条染色体，随机产生两个变异的位置并对其进行交换。变异算子的操作过程如图 4所示。

在遗传算法中，参数的交叉概率和变异概率对算法的性能有着较大的影响。对于交叉算子，在迭代前期交叉概率取大值为佳，能扩大搜索范围和加快进化速度。在后期交叉概率取小值为佳，使得种群相对稳定。对于变异算子，在迭代后期时，变异概率应当增加，以防止陷入局部极值，减弱种群的多样性。因此，本文采用简单遗传算法（Simple Genetic Algorithm，SGA）^[18]自适应的遗传概率，交叉概率$ {P}_{\mathrm{c}} $和变异概率$ {P}_{\mathrm{m}} $能够根据适应度自动做出改变，如式（15）、式（16）所示：

$ {{P}_{\text{c}}}=\left\{ \begin{align} & {{P}_{\text{c}1}}-({{P}_{\text{c}1}}-{{P}_{\text{c}2}})({f}'-{{f}_{\text{avg}}}){{f}_{\text{max}}}-{{f}_{\text{avg}}}, f\ge {{f}_{\text{avg}}} \\ & {{P}_{\text{c1}}}, {f}'<{{f}_{\text{avg}}} \\ \end{align} \right. $

(15)

$ {P}_{\mathrm{m}}=\left\{\begin{array}{l}{P}_{\mathrm{m}1}-\frac{({P}_{\mathrm{m}1}-{P}_{\mathrm{m}2})({f}_{\mathrm{m}\mathrm{a}\mathrm{x}}-f)}{{f}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{f}_{\mathrm{a}\mathrm{v}\mathrm{g}}}, f\ge {f}_{\mathrm{a}\mathrm{v}\mathrm{g}}\\ {P}_{\mathrm{m}1}, f <{f}_{\mathrm{a}\mathrm{v}\mathrm{g}}\end{array}\right. $

(16)

其中：$ {f}_{\mathrm{m}\mathrm{a}\mathrm{x}} $为每代群体中的最大适应度；$ {f}_{\mathrm{a}\mathrm{v}\mathrm{g}} $为每代群体中的平均适应度；$ {{f}'} $为需要交叉的两个个体中较大的适应度值；$ f $为需要变异的个体的适应度值。

3 实验与结果分析 3.1 实验平台与参数设置

为证明本文方法的可行性与高效性，将LBRA-KSP+MGA与SPA+MGA和LBRA-KSP+SGA方法进行对比分析。相关程序使用Python 3.7进行编写，硬件环境为Intel Core i5-7300HQ和16 GB RAM。所采用的IDE为PyCharm Community 2019.3版本。

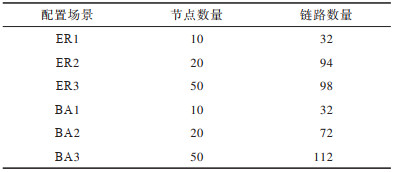
为了体现本文方法在各种应用场景下的普适性，首先采用与文献[16]相同的方法，产生随机的ER网络^[19]和随机的BA网络^[20]进行仿真验证，再针对真实的网络场景数据集进行仿真计算。对于随机生成流，源节点和目的节点在可选范围内随机生成，流负载值参考文献[9]进行设定，每条流在[1, 99]中任意选取。6种配置场景下的拓扑规模（节点数量与链路数量）如表 1所示。

本文采用MGA进行调度，由于MGA特性导致运行结果具有一定的随机性，因此为了保证数据的正确性，每组实验均进行5次并取其平均值作为最终数据。MGA算法参数设置如表 2所示。

3.2 结果分析

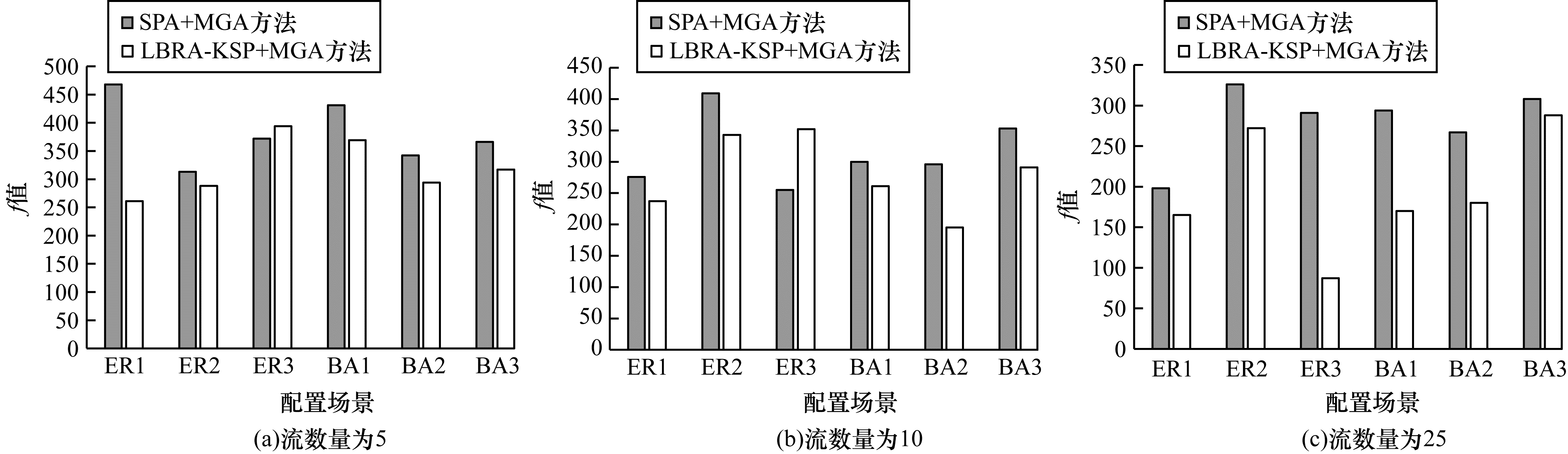
实验1  对比并分析LBRA-KSP路由算法与SPA路由算法对调度计算的影响（均使用MGA进行调度计算）。该实验采用表 1中的参数设置，对比在相同节点数量和相同流数量情况下，算法最终收敛的f值。图 5分别给出了流数量为5、10和25下的调度结果。可以看出，LBRA-KSP路由算法能够明显地降低每次调度的最大完成时间，而SPA路由算法仅考虑自身的最短路径，在流与流之间发生相互影响时，会导致调度时延的增加。而由于链路负载生成的随机性，可能会导致LBRA-KSP+MGA方法最终的最大适应度值f偏大，但是从统计意义上看，LBRA-KSP+MGA方法在整体上还是降低了f值，平均比SPA路由算法降低了23.11%。

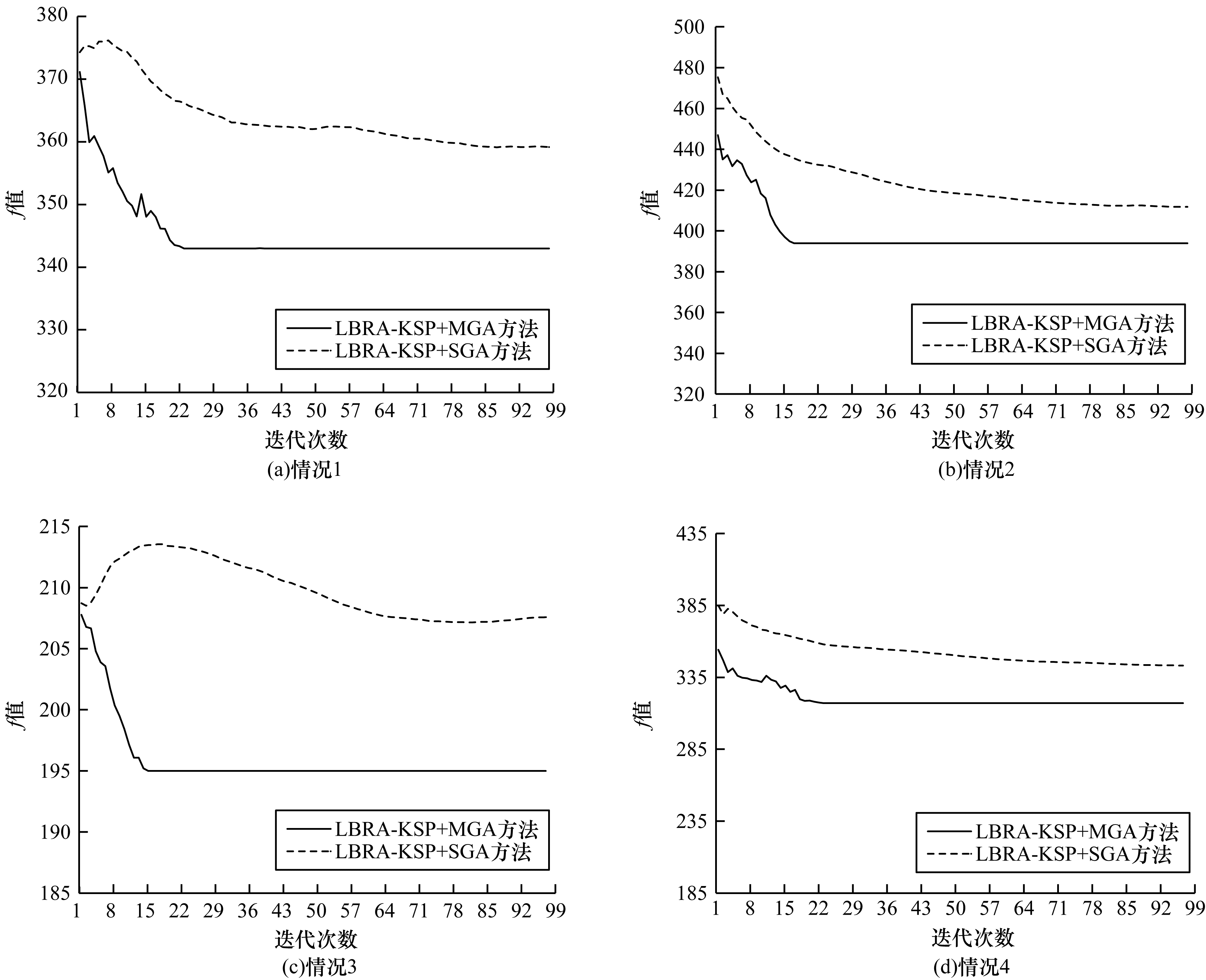
实验2  对比并分析MGA和SGA算法对调度计算的影响（均使用LBRA-KSP进行路由计算）。如图 6所示，该实验主要将LBRA-KSP+MGA和LBRA-KSP+SGA方法进行对比研究，观察收敛性能。实验分别选择以下4种情况进行对比分析：1）配置场景为ER2、节点数量为20、流数量为10；2）配置场景为ER3、节点数量为20、流数量为25；3）配置场景为BA2、节点数量为20、流数量为10；4）配置场景为BA3、节点数量为30、流数量为25。从图 6中可以看出，带有MGA的方法相较SGA方法明显迭代次数更少，收敛到的终值质量更优，并且随着网络规模的增加，最终收敛到的f值也会相应增大。

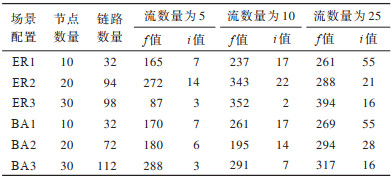
实验3  对比并分析不同节点数量和流数量对于LBRA-KSP+MGA方法调度计算的影响。该实验在ER1-ER3、BA1-BA3场景配置下，对应的节点数量分别设置为10、20和30，流数量分别为5、10和25。主要考察最终收敛到的f值与平均收敛的迭代次数i，经过仿真运行得到的结果如表 3所示。由于启发式算法的随机性和流负载生成的随机性，会导致部分数据比较特殊。从整体趋势上看，节点数量越多，调度最终收敛到的f值越大，而平均迭代次数i值会变小；从流数量的角度上看，随着流数量的增加，f值和i值都在不断增加，而ER和BA配置场景对调度的影响较小。

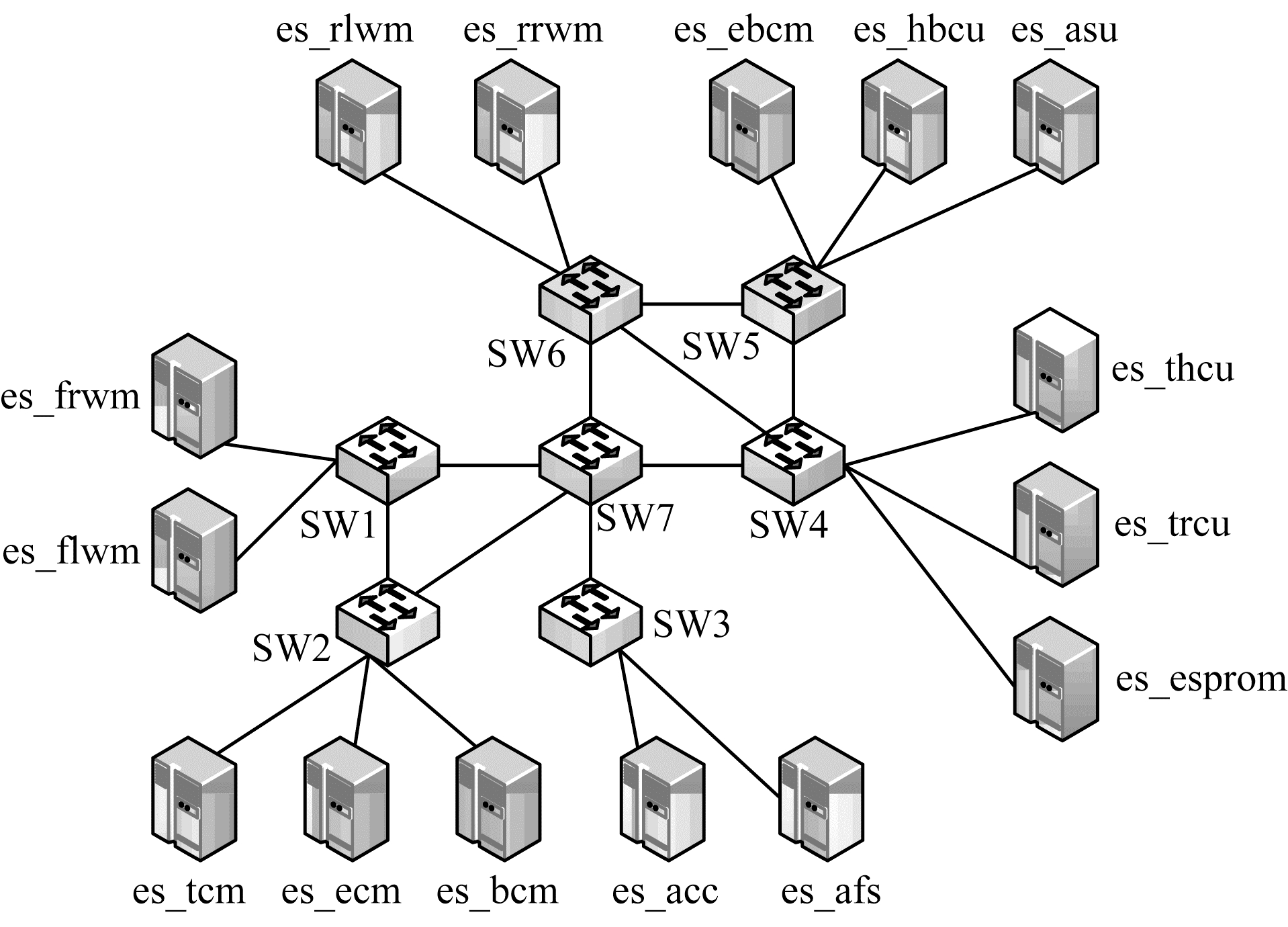
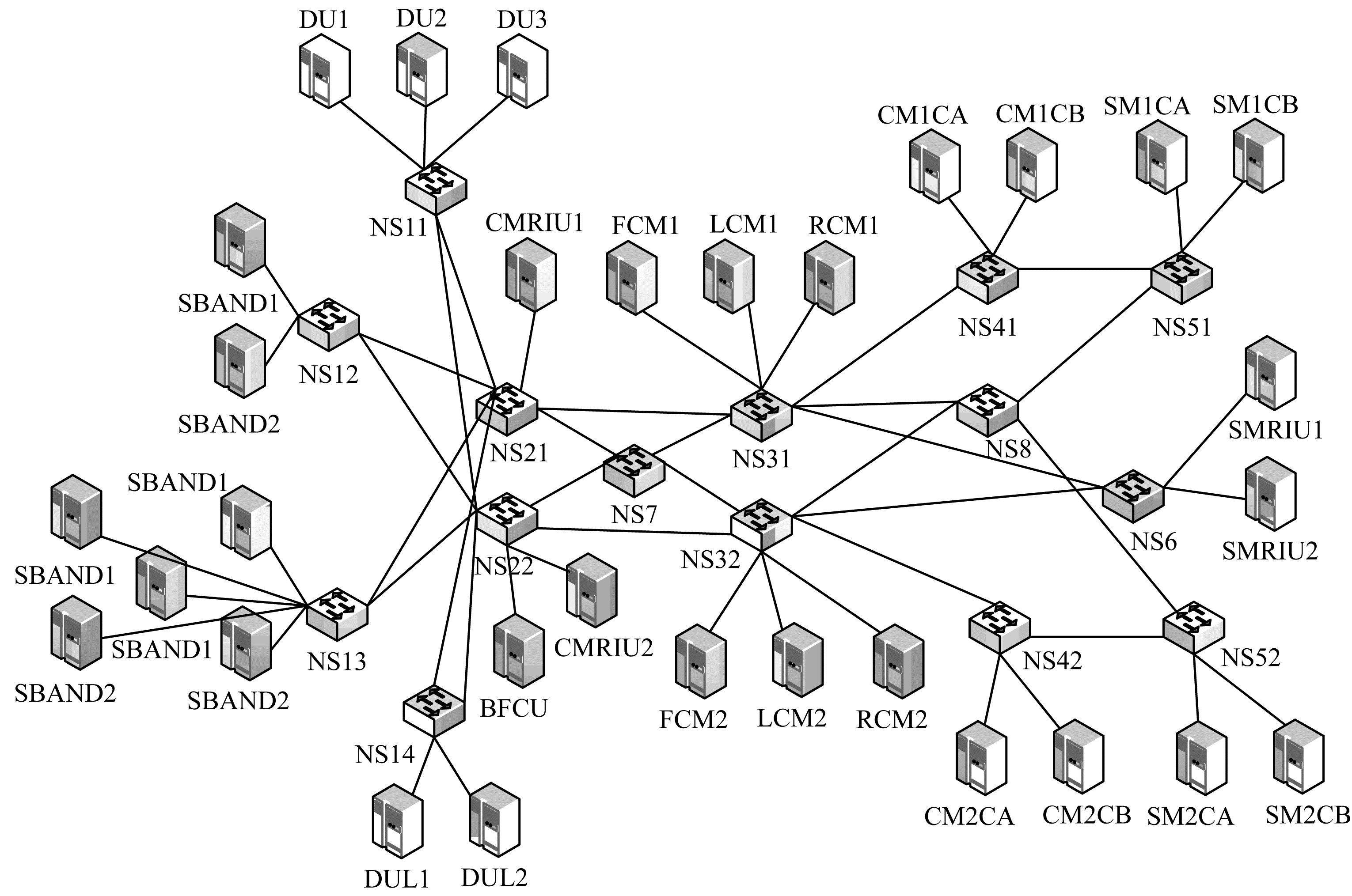
实验4  验证LBRA-KSP算法在真实网络环境下能进行有效的流量调度。对于有限带宽且多节点的控制系统、工业互联网、汽车内网等复杂大型系统中的内部网络，能够同时产生和传输多种不同QoS要求的流量。本文选取TSN领域中基于SAE环境和CEV环境的数据集^[2]。SAE和CEV环境下的拓扑结构如图 7、图 8所示，其中，SW1~SW7表示交换节点，es前缀表示终端节点。

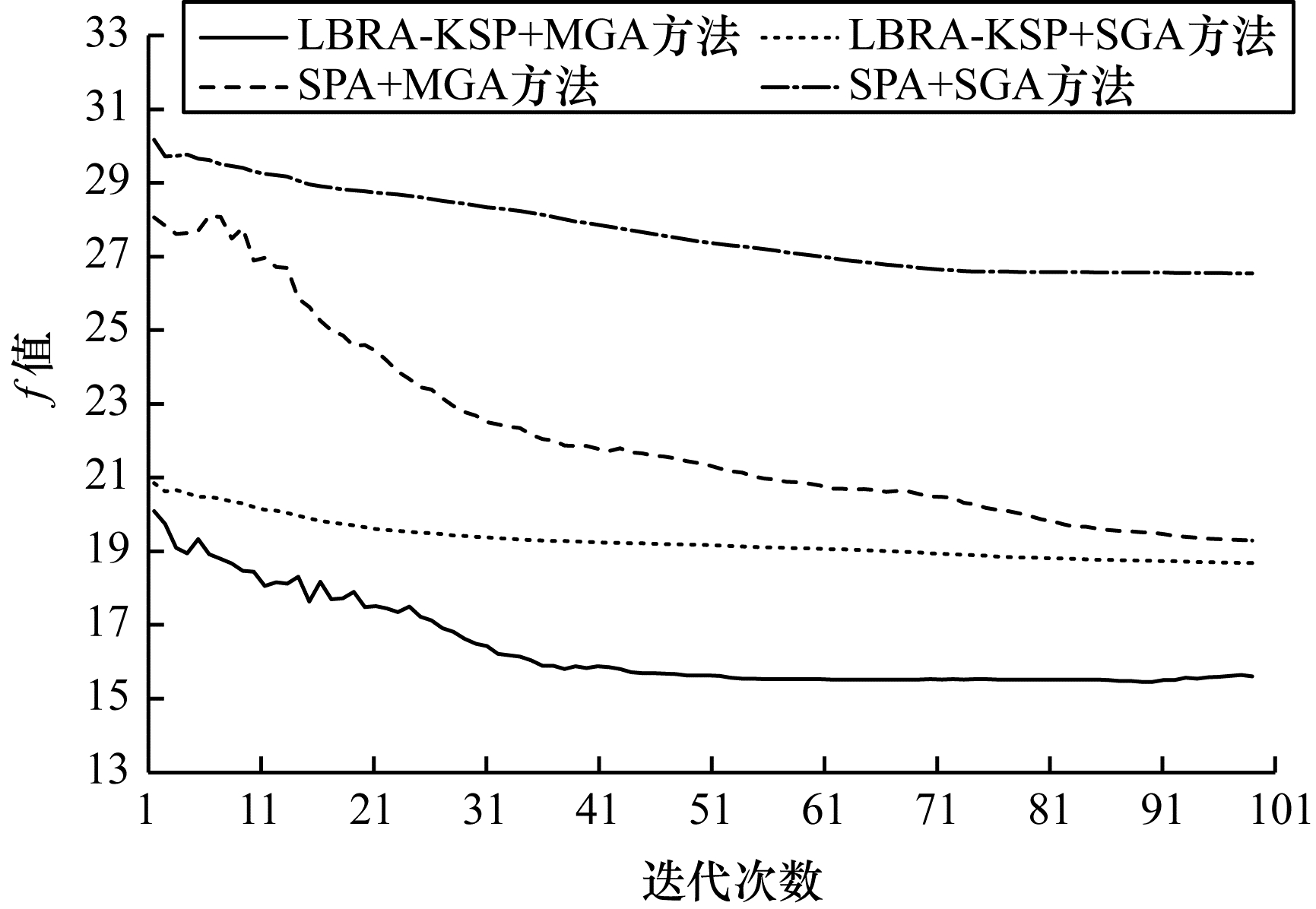
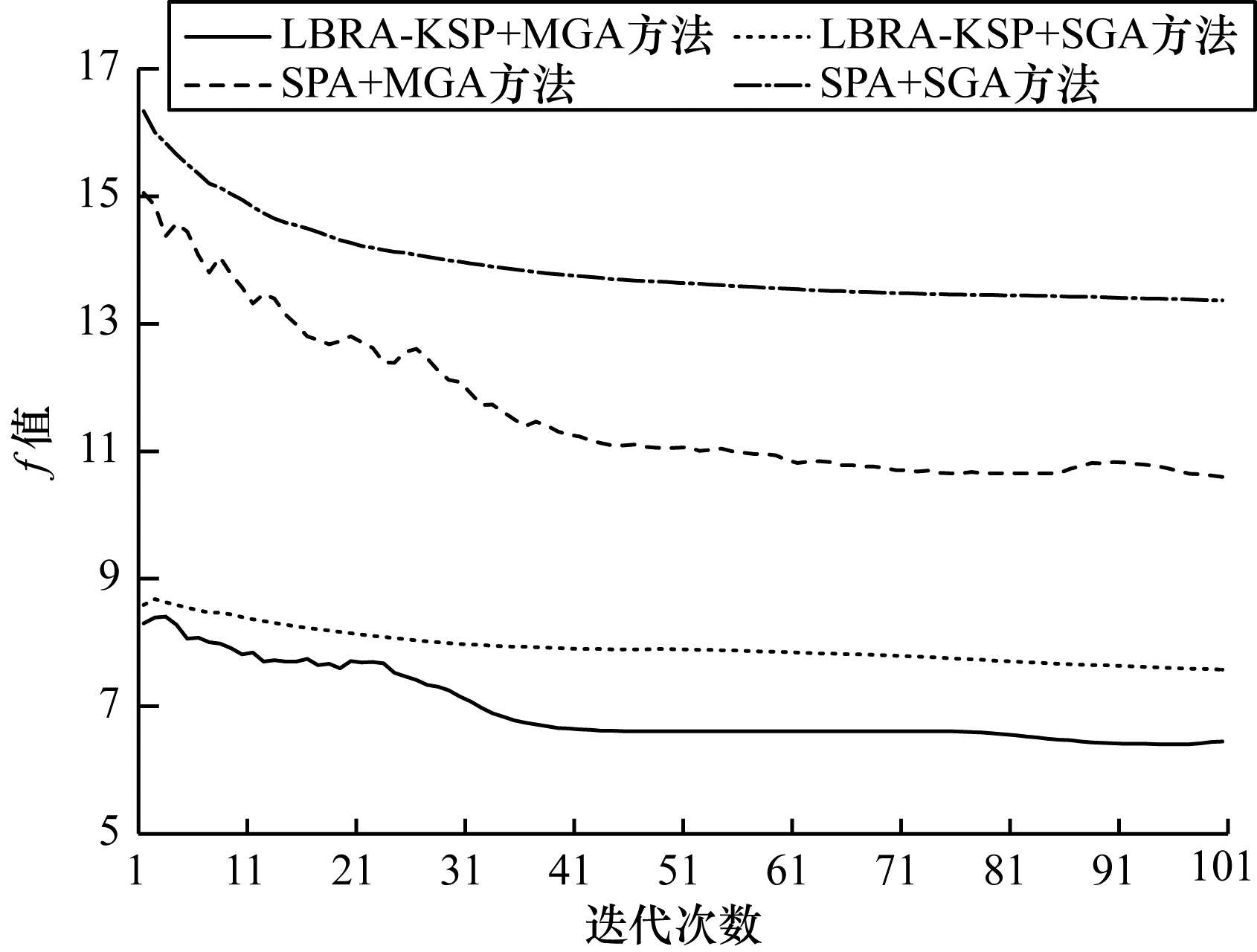
在数据预处理阶段，对于数据流按照式（3），针对不同实验拓扑将各条流整理为包含源端口、目的端口、流负载和流的端到端时延的四元组。在SAE环境中待调度的时间敏感数据流共有40条，在CEV环境中待调度的时间敏感数据流共有30条。该实验对比并分析了LBRA-KSP+MGA、LBRA-KSP+SGA、SPA+MGA、SPA+SGA这4种方法，运行结果如图 9、图 10所示。可以看出，在两种运行场景下，LBRA-KSP+MGA方法在收敛速度、最终f值的指标上均有明显优势，其收敛的平均迭代次数为52和46，最终的平均f值为15.58 ms和6.35 ms。考虑到路由的影响，LBRA-KSP相较SPA算法，最终f值分别下降了57.7%和59.4%，大幅减小了因为链路拥塞而导致的时延，而在调度上通过利用MGA算法，使计算结果快速收敛。可见，LBRA-KSP算法在真实网络环境下能进行有效的流量调度。

4 结束语

本文针对TSN时间敏感流量调度中存在的计算效率低、迭代收敛慢和路由路径之间相互影响等问题，提出一种基于最短路径负载均衡和改进遗传算法的流量调度方法。在路由计算上，解决了由于使用CSPF路由而导致的时延增加问题，借助链路负载均衡的思想，尽可能降低拥塞的发生概率。在调度计算上，对传统遗传算法选择算子的交叉与遗传概率进行改进，提升了迭代收敛的效率。仿真实验和真实网络环境实验结果表明，本文方法能够有效缩短时延敏感流量调度任务的完成时间，提高调度与路由计算效率。后续将在时间敏感流量调度计算的基础上添加其他数据流量进行计算，以实现更系统高效的流量调度。